以下各节介绍了关于烟灰形成理论的背景信息。有关在Ansys Fluent中使用烟灰形成模型的信息，请参阅用户指南中的“使用烟灰模型”部分。

9.2.1. 概述与限制

9.2.2. 烟灰模型理论

9.2.1 概述与限制

Ansys Fluent提供了五种模型用于预测燃烧系统中的烟灰形成。预测的烟灰浓度可以与P-1模型、离散坐标模型或离散传递辐射模型中的可变吸收系数相结合，用于辐射吸收。

9.2.1.1 预测烟灰形成

Ansys Fluent使用以下可用模型之一预测燃烧系统中的烟灰浓度：

• 一步法Khan和Greeves模型[301]（第1074页），Ansys Fluent基于经验关系预测烟灰形成速率。这是Ansys Fluent中的默认烟灰形成模型。

• 两步法Tesner模型[410]（第1080页），[652]（第1094页），Ansys Fluent预测核粒子的形成并计算核上的烟灰形成。在这些和之前的模型中，假设烟灰（和粒子核）的燃烧受Magnussen燃烧速率[410]（第1080页）控制。这一假设限制了这些模型仅适用于湍流流动。烟灰形成的详细化学和物理过程非常复杂，这两个模型都是基于经验的，可用于近似燃烧系统中的烟灰形成过程。这些模型产生的结果应视为系统性能的定性指标，除非通过实验结果验证。

• Moss-Brookes 模型 [81]（第 1061 页），其中 Ansys Fluent 通过求解归一化自由基核浓度和烟灰质量分数的输运方程，预测甲烷火焰（以及适当修改后的高级碳氢化合物）的烟灰形成。该模型具有较少的经验性，理论上应比 Khan 和 Greeves 以及 Tesner 模型提供更高的精度。

• Moss-Brookes-Hall 模型 [228]（第 1070 页），是 Moss-Brookes 模型的扩展，适用于高级碳氢燃料（例如煤油）。Hall 扩展为高级碳氢燃料的建模提供了更多选项。请注意，Moss-Brookes-Hall 模型仅在所需物种存在于气相物种列表中时可用。

• 矩量法模型 [192]（第 1068 页），Ansys Fluent 基于烟灰颗粒群平衡方法预测烟灰形成。矩量法考虑了烟灰粒径分布，其中烟灰颗粒的直径动态变化。该方法在模拟各种烟灰形成子过程（如成核、凝聚和表面生长核）时使用较少的经验常数。

9.2.1.2 烟灰建模限制

以下限制适用于烟灰形成模型：

• 必须使用基于压力的求解器。烟灰模型不适用于任何基于密度的求解器。

• Khan 和 Greeves 模型以及 Tesner 模型仅能模拟湍流中的烟灰形成，而 Moss-Brookes 模型、Moss-Brookes-Hall 模型和矩量法模型可用于层流和湍流。

• 烟灰模型不能与预混燃烧模型同时使用。

9.2.2 烟灰模型理论

9.2.2.1 单步烟灰形成模型

在一步 Khan 和 Greeves 模型 [301]（第 1074 页）中，Ansys Fluent 求解单个烟灰质量分数的输运方程：

$$\frac{\partial }{\partial t}\left(\rho Y_{soot}\right)+\nabla \cdot \left(\rho \overrightarrow{v}{Y}_{soot}\right)=\nabla \cdot \left(\frac{{\mu }_t}{{\sigma }_{soot}}\nabla Y_{soot}\right)+{\Re }_{soot}\text{\hspace{1em}(9.115)}$$

(9.115)

其中

$Y_{\text{soot }}=$ 烟灰质量分数

${\sigma }_{\text{soot }}=$ 烟灰输运的湍流普朗特数

${\mathcal{R}}_{\text{soot }}=$ 烟灰生成净速率 $\left(\mathrm{kg}/{\mathrm{m}}^3-\mathrm{s}\right)$

${\mathcal{R}}_{\text{soot }}$，即烟灰生成净速率，是烟灰形成速率 ${\mathcal{R}}_{\text{soot, form }}$ 和烟灰燃烧速率 ${\mathcal{R}}_{\text{soot, comb }}$ 的平衡结果：

$${\mathcal{R}}_{\text{soot }}={\mathcal{R}}_{\text{soot, form }}-{\mathcal{R}}_{\text{soot, comb }}\text{\hspace{1em}(9.116)}$$

烟灰生成速率可以通过一个简单的经验速率表达式来表示：

$${\mathcal{R}}_{\text{soot, form }}=C_s{p}_{\text{fuel }}{\varphi }^r{e}^{-E/RT}\text{\hspace{1em}(9.117)}$$

以下是翻译成中文的文本：

在哪里

$$C_s=\text{soot formation constant}\left(\mathrm{kg}/\mathrm{N}-\mathrm{m}-\mathrm{s}\right)$$

$p_{\text{fuel}}=$ 燃料分压（帕）

$\varphi =$ 当量比

$r=$ 当量比指数

$E/R=$ 活化温度（K）

炭黑燃烧速率是两个速率表达式中的最小值 [410]（第1080页）：

$${\mathcal{R}}_{\text{soot, comb }}=\min \left[{\mathcal{R}}_1,{\mathcal{R}}_2\right]\text{\hspace{1em}(9.118)}$$

两项费率计算如下：

$${\mathcal{R}}_1=A\rho Y_{\text{soot }}\frac{\epsilon }{k}\text{\hspace{1em}(9.119)}$$

以及

$${\mathcal{R}}_2=A\rho \left(\frac{Y_{\text{ox }}}{v_{\text{soot }}}\right)\left(\frac{Y_{\text{soot }}{v}_{\text{soot }}}{Y_{\text{soot }}{v}_{\text{soot }}+Y_{\text{fuel }}{v}_{\text{fuel }}}\right)\frac{\epsilon }{k}\text{\hspace{1em}(9.120)}$$

其中

$A=$ Magnussen模型中的常数

$Y_{ox},Y_{\text{fuel }}=$ 氧化剂和燃料的质量分数

$v_{\text{soot }},v_{\text{fuel }}=$ 烟尘和燃料燃烧的质量化学计量比

一步模型中的默认常数适用于广泛范围的碳氢燃料。

9.2.2.2 两步烟尘生成模型

两步Tesner模型[652]（第1094页）预测自由基核的生成，然后在这些核上计算烟尘的形成。因此，Ansys Fluent求解两个标量量的输运方程：烟尘质量分数（公式9.115（第395页））和归一化的自由基核浓度：

$$\frac{\partial }{\partial t}\left(\rho b_{nuc}^{\ast }\right)+\nabla \cdot \left(\rho \overrightarrow{v}{b}_{nuc}^{\ast }\right)=\nabla \cdot \left(\frac{{\mu }_t}{{\sigma }_{nuc}}\nabla b_{nuc}^{\ast }\right)+{\Re }_{nuc}^{\ast }\text{\hspace{1em}(9.121)}$$

其中

$b_{\text{nuc }}^{\ast }$ = 归一化自由基核浓度（粒子数）$\times {10}^{-15}/\mathrm{kg}$

${\sigma }_{\text{nuc }}$ = 核传输的湍流普朗特数

${\mathbf{\Re }}_{\text{nuc }}^{\ast }$ = 归一化净核生成速率（粒子数）$\times {10}^{-15}/{\mathrm{m}}^3-\mathrm{s}$

在这些传输方程中，核和烟灰的生成速率是净速率，涉及形成和燃烧之间的平衡。

9.2.2.2.1 烟灰生成速率

两步模型以与单步模型相同的方式计算烟灰的净生成速率，${\mathcal{R}}_{\text{soot }}$，作为烟灰形成和烟灰燃烧之间的平衡：

$${\mathcal{R}}_{\text{soot }}={\mathcal{R}}_{\text{soot, form }}-{\mathcal{R}}_{\text{soot, comb }}\text{\hspace{1em}(9.122)}$$

然而，在两步模型中，积碳生成的速率，${\mathcal{R}}_{soot,form}$ ，取决于自由基核的浓度，$c_{nuc}$ ：

$${\mathcal{R}}_{\text{soot, form }}=m_p\left(\alpha -\beta N_{\text{soot }}\right)c_{\text{nuc }}\text{\hspace{1em}(9.123)}$$

其中：

$m_p=$ 炭烟颗粒平均质量（kg/颗粒数）

$N_{\text{soot }}=$ 炭烟颗粒浓度（颗粒数/${\mathrm{m}}^3$）

$c_{\text{nuc }}=$ 自由基核浓度 $=\rho b_{\text{nuc }}$（颗粒数/${\mathrm{m}}^3$）

$\alpha =$ 经验常数 $\left({\mathrm{s}}^{-1}\right)$

$\beta =$ 经验常数 $({\mathrm{m}}^3/\text{颗粒数-s})$

炭烟燃烧速率 ${\mathcal{R}}_{\text{soot, comb }}$ 的计算方式与一步模型相同，使用公式 9.118（第 395 页）至公式 9.120（第 396 页）。

两步模型的默认常数适用于乙炔 $\left({\mathrm{C}}_2{\mathrm{H}}_2\right)$ 的燃烧。根据 Ahmad 等人 [10]（第 1057 页）的研究，这些数值应根据不同燃料进行调整，因为乙炔的炭烟生成特性与饱和烃燃料已知有所不同。

9.2.2.2.2 自由基核生成速率

两步模型中，自由基核的净生成速率由自由基核形成速率与自由基核燃烧速率的平衡给出：

$${\mathfrak{R}}_{\text{nuc }}^{\ast }={\mathfrak{R}}_{\text{nuc, form }}^{\ast }-{\mathfrak{R}}_{\text{nuc, comb }}^{\ast }\text{\hspace{1em}(9.124)}$$

${\mathcal{R}}_{\text{nuc, form }}^{\ast }=$ 核形成速率（粒子数 $\times {10}^{-15}/{\mathrm{m}}^3-\mathrm{s}\text{)}$

${\mathcal{R}}_{\text{nuc, comb }}^{\ast }=$ 核燃烧速率（粒子数 $\times {10}^{-15}/{\mathrm{m}}^3-\mathrm{s}\text{)}$

核形成速率 ${\mathfrak{R}}_{nuc,form}^{\ast }$ 取决于自发的形成和分支过程，这一过程由

$${\Re }_{\text{nuc, form }}^{\ast }={\eta }_0+\left(f-g\right)c_{\text{nuc }}^{\ast }-g_0{c}_{\text{nuc }}^{\ast }{N}_{\text{soot }}\text{\hspace{1em}(9.125)}$$

$${\eta }_0=a_0^{\ast }{c}_{\text{fuel }}{e}^{-E/RT}\text{\hspace{1em}(9.126)}$$

其中：

$c_{\text{nuc }}^{\ast }$ 为归一化的核浓度（$\left(=\rho b_{\text{nuc }}^{\ast }\right)$）

$a_0^{\ast }=a_0/{10}^{15}$

$a_0$ 为指前速率常数（粒子数/kg-s）

$c_{\text{fuel }}$ 为燃料浓度（$\left(\mathrm{kg}/{\mathrm{m}}^3\right)$）

$f-g$ 为线性分支-终止系数（$\left({\mathrm{s}}^{-1}\right)$）

$g_0$ 为炭黑颗粒上的线性终止（$({\mathrm{m}}^3/$ 粒子数-s）

注意，在公式 9.125（第 397 页）中的分支项 $\left(f-g\right)c_{nuc}^{\ast }$，仅当动力学速率 ${\eta }_0$ 大于极限形成速率（默认值为 ${10}^5$ 粒子数/ ${\mathrm{m}}^3$ -s）时才包含。

核燃烧速率假设与炭黑燃烧速率成正比：

$${\mathcal{R}}_{\text{nuc, comb }}^{\ast }={\mathcal{R}}_{\text{soot, comb }}\frac{b_{\text{nuc }}^{\ast }}{Y_{\text{soot }}}\text{\hspace{1em}(9.127)}$$

烟灰燃烧速率 ${\mathcal{R}}_{\text{soot, comb }}$ 由公式 9.118 (第 395 页) 给出。

9.2.2.3 Moss-Brookes 模型

Moss-Brookes 模型求解了归一化自由基核浓度 $b_{nuc}^{\ast }$ 和烟灰质量分数 $Y_{\text{soot }}$ 的传输方程：

$$\begin{array}{ccc}\frac{\partial }{\partial t}\left(\rho Y_{soot}\right)+\nabla \cdot \left(\rho \overrightarrow{v}{Y}_{soot}\right)& =& \nabla \cdot \left(\frac{{\mu }_t}{{\sigma }_{soot}}\nabla Y_{soot}\right)\\ & +& \frac{dM}{dt}\end{array}\text{\hspace{1em}(9.128)}$$

$$\begin{array}{ccc}\frac{\partial }{\partial t}\left(\rho b_{nuc}^{\ast }\right)+\nabla \cdot \left(\rho \overrightarrow{v}{b}_{nuc}^{\ast }\right)& =& \nabla \cdot \left(\frac{{\mu }_t^{\text{’}}}{{\sigma }_{nuc}}\nabla b_{nuc}^{\ast }\right)\\ & +& \frac{1}{N_{norm}}\frac{dN}{dt}\end{array}\text{\hspace{1em}(9.129)}$$

其中

$Y_{\text{soot }}=\text{炭黑质量分数}$

$M=\text{炭黑质量浓度}\left(\mathrm{kg}/{\mathrm{m}}^3\right)$

$b_{\text{nuc }}^{\ast }=\text{归一化自由基核浓度（粒子数}\times {10}^{-15}/\mathrm{kg}\text{）}=\frac{N}{\rho N_{\text{norm }}}$

$N=\text{炭黑粒子数密度（粒子数}/{\mathrm{m}}^3\text{）}$

$N_{\text{norm }}={10}^{15}\text{粒子数}$

炭黑粒子的瞬时生成速率，受气相成核和自由分子区凝聚作用的影响，由以下公式给出：

$$\frac{dN}{dt}=\underset{\text{Nucleation }}{\underbrace{C_{\alpha }{N}_A{\left(\frac{X_{\text{prec }}P}{RT}\right)}^l\exp \left\{-\frac{T_{\alpha }}{T}\right\}}}-\underset{\text{Coagulation }}{\underbrace{C_{\beta }{\left(\frac{24RT}{{\rho }_{\text{soot }}{N}_A}\right)}^{1/2}{d}_p^{1/2}{N}^2}}\text{\hspace{1em}(9.130)}$$

其中，$C_{\alpha }$、$C_{\beta }$ 和 $l$ 是模型常数。这里，$N_A\left(=6.022045\times {10}^{26}\mathrm{kmol}{}^{-1}\right)$ 是阿伏伽德罗常数，$X_{\text{prec }}$ 是炭黑前驱物的摩尔分数（对于甲烷，前驱物假定为乙炔，而对于煤油，则是乙炔和苯的组合）。炭黑的质量密度 ${\rho }_{\text{soot }}$ 假定为 $1800\mathrm{kg}/{\mathrm{m}}^3$，$d_p$ 是炭黑颗粒的平均直径。炭黑颗粒的成核速率被认为与当地的乙炔浓度成正比。成核反应的活化温度 $T_{\alpha }$ 由 Lindstedt [378]（第 1079 页）提出。

炭黑质量浓度的源项由以下表达式建模： $$\begin{array}{rl}\frac{dM}{dt}& =\underset{\text{成核}}{\underbrace{M_P{C}_{\alpha }{\left\{\frac{X_{prec}P}{RT}\right\}}^l\exp \left\{-\frac{T_{\alpha }}{T}\right\}}}\\ & +\underset{\text{表面生长}}{\underbrace{C_{\gamma }{\left(\frac{X_{sgsP}}{RT}\right)}^m\exp \left\{-\frac{T_{\gamma }}{T}\right\}{\left[{\left(\pi N\right)}^{1/3}{\left(\frac{6M}{{\rho }_{soot}}\right)}^{2/3}\right]}^n}}\\ & -\underset{\text{氧化}}{\underbrace{C_{oxid}{C}_{\omega }{\eta }_{coll}\left(\frac{X_{OH}P}{RT}\right)\sqrt{T}{\left(\pi N\right)}^{1/3}{\left(\frac{6M}{{\rho }_{soot}}\right)}^{2/3}}}\end{array}\text{\hspace{1em}(9.131)}$$

其中，$C_{\gamma }$、$C_{\text{oxid }}$、$C_{\omega }$、$m$ 和 $n$ 是额外的模型常数。常数 $M_P\left(=144\mathrm{kg}/\mathrm{kmol}\right)$ 是一个初始炭黑颗粒的质量，这里假定由 12 个碳原子组成。尽管模型对这一假设不敏感，但需要一个非零的初始质量来开始表面生长过程。这里，$X_{sgs}$ 是参与表面生长物种的摩尔分数。对于石蜡燃料，炭黑颗粒主要通过在其表面添加气体物种，特别是乙炔来生长，乙炔在层流甲烷扩散火焰的炭黑生成区域中含量丰富。

该模型假设羟基自由基是甲烷/空气扩散火焰中的主要氧化剂，并且炭黑通过 $\mathrm{OH}$ 自由基的表面特定氧化速率可以根据 Fenimore 和 Jones [173]（第 1066 页）提出的模型来制定。假设碰撞效率 $\left({\eta }_{\text{coll }}\right)$ 为 0.04，氧化速率可以写成方程 9.131（第 398 页）。

确定指数 ( l, m ) 和 ( n ) 的过程在 Brookes 和 Moss [81]（第 1061 页）中有详细解释。常数 ( C_{\alpha} ) 和 ( C_{\beta} ) 是通过对存在实验数据的层流火焰进行数值模拟来确定的。

Brookes 和 Moss 为甲烷火焰提出的常数集合如下：

( C_{\alpha} = 54 ; \text{s}^{-1} )（炭黑生成速率的模型常数）

( T_{\alpha} = 21000 ; \text{K} )（炭黑生成的活化温度）

( C_{\beta} = 1.0 )（凝结速率的模型常数）

( C_{\gamma} = 11700 ; \text{kg} ; \text{m} ; \text{kmol}^{-1} ; \text{s}^{-1} )（表面生长速率的缩放因子）

( T_{\gamma} = 12100 ; \text{K} )（表面生长速率的活化温度）

( C_{\omega} = 105.8125 ; \text{kg} ; \text{m} ; \text{kmol}^{-1} ; \text{K}^{1/2} ; \text{s}^{-1} )（氧化模型常数）

$${\eta }_{\text{coll }}=0.04\text{(collisional efficiency parameter)}$$

$$C_{\text{oxid }}=0.015\text{(oxidation rate scaling parameter)}$$

请注意，Ansys Fluent 中 Moss-Brookes 模型的实现使用了上述列出的值，除了 $C_{\text{oxid }}$，默认设置为单位值。

上述方程中平均烟灰源项的闭合方法也由 Brookes 和 Moss [81]（第 1061 页）详细描述。不相关的闭合方法是解决上述输运方程的首选选项。

Moss 等人 [463]（第 1084 页）展示了上述模型应用于煤油火焰，通过仅修改烟灰前驱物种（在原始模型中前驱物是乙炔，而对于煤油火焰，前驱物被假定为乙炔和苯的组合）并设置氧化缩放参数 $C_{\text{oxid }}$ 为单位值。在较低压力（7 巴）条件下，与实验测量结果的良好对比被观察到。对于甲烷火焰中的烟灰形成预测显示，Brooks 和 Moss [81]（第 1061 页）模型相比标准的 Tesner 等人 [652]（第 1094 页）公式更为优越。

9.2.2.3.1 Moss-Brookes-Hall 模型

由于 Moss-Brookes 模型主要针对甲烷火焰开发和验证，Ansys Fluent 中还提供了进一步扩展用于更高碳氢燃料的 Moss-Brookes-Hall 模型。在这里，扩展版本是 Wen 等人 [701]（第 1097 页）报告的模型，基于 Hall 等人 [228]（第 1070 页）提出的模型扩展和 Lee 等人 [349]（第 1077 页）提出的氧化模型。Hall [228]（第 1070 页）的工作基于双环和三环芳香族的烟灰起始速率，与 Moss-Brookes 假设的乙炔或苯（对于更高碳氢化合物）的烟灰起始不同。

Hall等人[228]（第1070页）提出了一种基于形成双环和三环芳香烃（${\mathrm{C}}_{10}{\mathrm{H}}_7$和${\mathrm{C}}_{14}{\mathrm{H}}_{10}$）的形成速率的烟炱起始速率，这些芳香烃由乙炔（${\mathrm{C}}_2{\mathrm{H}}_2$）、苯（${\mathrm{C}}_6{\mathrm{H}}_6$）和苯基自由基（${\mathrm{C}}_6{\mathrm{H}}_5$）通过以下机制形成：

$$\begin{array}{ll}2{\mathrm{C}}_2{\mathrm{H}}_2+{\mathrm{C}}_6{\mathrm{H}}_5& \rightleftharpoons {\mathrm{C}}_{10}{\mathrm{H}}_7+{\mathrm{H}}_2\\ {\mathrm{C}}_2{\mathrm{H}}_2+{\mathrm{C}}_6{\mathrm{H}}_6+{\mathrm{C}}_6{\mathrm{H}}_5& \rightleftharpoons {\mathrm{C}}_{14}{\mathrm{H}}_{10}+\mathrm{H}+{\mathrm{H}}_2\end{array}\text{\hspace{1em}(9.132)}$$

根据他们的层流甲烷火焰数据，炭黑颗粒的起始生成速率被确定为物种${\mathrm{C}}_{10}{\mathrm{H}}_7$和${\mathrm{C}}_{14}{\mathrm{H}}_{10}$形成速率的八倍，如所示。

$$\begin{array}{rl}{\left(\frac{dN}{dt}\right)}_{inception}& =8C_{\alpha ,1}\frac{N_A}{M_P}\left[{\rho }_{soot}^2\right(\frac{Y_{C_2{H}_2}}{W_{C_2{H}_2}}{)}^2\frac{Y_{C_6{H}_5}{W}_{H_2}}{W_{C_6{H}_5}{Y}_{H_2}}\left]\exp \right\{-\frac{T_{\alpha ,1}}{T}\}\\ & +8C_{\alpha ,2}\frac{N_A}{M_P}\left[{\rho }_{soot}^2\right(\frac{Y_{C_2{H}_2}}{W_{C_2{H}_2}}{)}^2\frac{Y_{C_6{H}_5}{W}_{H_2}}{W_{C_6{H}_5}{Y}_{H_2}}\left]\exp \right\{-\frac{T_{\alpha ,2}}{T}\}\end{array}\text{\hspace{1em}(9.133)}$$

根据Hall等人[228]（第1070页）的确定，参数为：$C_{\alpha ,1}=127\times {10}^{888}{\mathrm{s}}^{-1}$，$C_{\alpha ,2}=178\times {10}^{9.50}{\mathrm{s}}^{-1}$，$T_{\alpha ,1}=4378\mathrm{K}$，以及$T_{\alpha ,2}=6390\mathrm{K}$。在他们的模型中，假设初生烟尘颗粒的质量为$1200\mathrm{kg}/\mathrm{kmol}$（对应于100个碳原子，而不同于Brookes和Moss[81]（第1061页）所用的12个碳原子）。烟尘的质量密度假设为$2000\mathrm{kg}/{\mathrm{m}}^3$，这与Brookes和Moss[81]（第1061页）所用的值略有不同。

凝并项和表面生长项的公式与Brookes和Moss[81]（第1061页）所用的相似，但对常数$C_{\gamma }$进行了微调，使其值为$9000.6\mathrm{kg}\mathrm{m}{\mathrm{kmol}}^1{\mathrm{s}}^{-1}$（基于Lindstedt[379]（第1079页）开发的模型）。

对于烟尘氧化项，除了羟基自由基引起的烟尘氧化外，还增加了基于Lee等人[349]（第1077页）的测量和模型所得到的${\mathrm{O}}_2$引起的氧化。通过假设表面反应的动力学是限制机制，并且颗粒足够小以至于可以忽略扩散效应对烟尘氧化的影响，他们推导出了分子氧对烟尘氧化的特定速率。因此，包括羟基自由基引起的氧化在内的完整烟尘氧化项，其形式为...

$$\begin{array}{rl}{\left(\frac{dM}{dt}\right)}_{oxid}& =-C_{oxid}{C}_{\omega ,1}{\eta }_{coll}\left(\frac{X_{OH}P}{RT}\right)\sqrt{T}{\left(\pi N\right)}^{1/3}{\left(\frac{6M}{{\rho }_{soot}}\right)}^{2/3}\\ & -C_{oxid}{C}_{\omega ,2}(\frac{X_{O_2}P}{RT})\exp \left\{-\frac{T_{\omega ,2}}{T}\right\}\sqrt{T}(\pi N{)}^{1/3}{\left(\frac{6M}{P_{soot}}\right)}^{2/3}\end{array}\text{\hspace{1em}(9.134)}$$

在此，碰撞效率假定为0.13（相较于Brookes和Moss使用的0.04值），氧化速率缩放参数设为0.015。所采用的模型常数如下：

$C_{\omega ,1}=105.81\mathrm{kg}\mathrm{m}{\mathrm{kmol}}^1{\mathrm{K}}^{1/2}{\mathrm{s}}^{-1}\text{（与Brookes和Moss所用相同）}$

$C_{\omega ,2}=8903.51\mathrm{kg}\mathrm{m}{\mathrm{kmol}}^1{\mathrm{K}}^{1/2}{\mathrm{s}}^{-1}$

$T_{\omega ,2}=19778\mathrm{K}$

9.2.2.3.2 湍流流动中的煤烟形成

Moss-Brookes模型及其Hall扩展的煤烟形成与破坏的动力学机制，如同${\mathrm{NO}}_{\mathrm{x}}$模型一样，源自实验室实验。然而，在任何实际燃烧系统中，流动都是高度湍流的。湍流混合过程导致温度和物种浓度随时间波动，这将影响火焰的特性。

煤烟形成速率、温度和物种浓度之间的关系高度非线性。因此，如果在任何模型中采用时间平均的组成和温度来预测平均煤烟形成速率，将会产生显著误差。必须通过考虑描述时间变化的概率密度函数来考虑温度和组成波动。

9.2.2.3.2.1 湍流-化学相互作用模型

在湍流燃烧计算中，Ansys Fluent求解密度加权时间平均的Navier-Stokes方程，用于温度、速度和物种浓度或平均混合分数及方差。为了计算Moss-Brookes模型和Hall扩展的煤烟浓度，必须在域内每一点使用平均流动场信息计算时间平均的煤烟形成速率。

9.2.2.3.2.2 PDF方法

PDF方法已被证明在湍流流动的理论描述中非常有用[280]（第1073页）。在Ansys Fluent Moss-Brookes模型和Hall扩展模型中，使用关于归一化温度、物种质量分数或两者的组合的单变量或联合变量PDF来预测烟灰的形成。如果使用非预混燃烧模型来模拟燃烧，那么也可以使用关于混合分数的单变量或双变量PDF。用于PDF构建的独立变量的平均值是通过求解输运方程得到的。

9.2.2.3.2.3 平均反应速率

《平均反应速率的一般表达式》（第391页）中描述的${\mathrm{NO}}_{\mathrm{x}}$模型的平均湍流反应速率也适用于Moss-Brookes模型和Hall扩展模型。

PDF用于对烟灰的瞬时生成速率进行加权，并通过在适当范围内进行积分，如公式9.105（第392页）和公式9.106（第392页）所述，以获得平均湍流反应速率。

9.2.2.3.2.4 PDF选项

与${\mathrm{NO}}_{\mathrm{x}}$模型的情况一样，$P$可以计算为双矩beta函数或截断高斯函数，适用于燃烧计算[231]（第1070页），[444]（第1082页）。公式9.108（第392页）至公式9.112（第393页）也适用于Moss-Brookes模型和Hall扩展模型，其中方差${\sigma }^2$在燃烧计算阶段通过求解输运方程，使用公式9.113（第393页）或公式9.114（第393页）来计算。

9.2.2.3.3 烟灰对辐射吸收系数的影响

《烟灰对吸收系数的影响》（第219页）提供了烟灰-辐射相互作用建模的描述。

9.2.2.4 矩方法模型

为了准确预测积碳的形成，需要对积碳形成的详细动力学进行建模，并解析颗粒大小分布。矩量法，即仅求解少数几个矩，是一种计算效率高的积碳形成建模方法。

9.2.2.4.1 积碳颗粒群体平衡

在积碳形成过程中，积碳颗粒存在多种直径。颗粒群体平衡方法利用颗粒大小分布（PSD）来模拟积碳颗粒表面积，该表面积涉及积碳形成过程中重要子步骤的计算，如积碳颗粒表面生长和氧化。积碳形成的各个阶段对积碳PSD产生影响。积碳颗粒群体的演变可以通过群体平衡方程来表示，也称为斯莫卢霍夫斯基主方程：

$$\begin{array}{rl}\frac{d{N}_1}{dt}=& -\sum _{j=1}^{\infty }{\beta }_{1,j}{N}_1{N}_j\\ \frac{d{N}_i}{dt}=& \frac{1}{2}\sum _{j=1}^{i-1}{\beta }_{j,i-j}{N}_{i-j}{N}_j-\sum _{j=1}^{\infty }{\beta }_{i,j}{N}_i{N}_j\end{array}\text{\hspace{1em}(9.135)}$$

其中，$N_i$ 是颗粒数密度函数，表示单位体积内第 $i^{\text{th}}$ 尺寸类别的烟尘颗粒数量，${\beta }_{i,j}$ 是尺寸类别为 $i$ 和 $j$ 的颗粒之间的碰撞系数。

对于第一个颗粒尺寸类别（第一个方程），右侧只包含一个负源项。这一项反映了由于当前尺寸类别的颗粒与其他任何颗粒的凝聚作用，导致第一个尺寸类别数量减少，从而形成更大尺寸类别颗粒的情况。对于所有其他更高颗粒尺寸类别，右侧的第二个方程中出现正源项，表明由于较低尺寸类别颗粒之间的凝聚作用，颗粒数密度函数 $N_i$ 的增长。

求解方程 9.135（第 402 页）的主要困难在于需要求解无限多个颗粒尺寸类别。处理这类问题的两种常用方法是分段法和矩量法。

分段法基于将整个颗粒尺寸类别范围离散化为预定义的有限数量区间。考虑到颗粒质量和数量将分布在所有区间，并受到其他过程（如表面反应和氧化）的影响，为了获得准确的解，需要足够多的区间（或有限区间）。因此，将分段法应用于方程 9.135（第 402 页）在计算上要求较高。分段法的一个高效替代方案是矩量法。该方法考虑了烟尘粒径分布函数（PSD）的矩。

颗粒尺寸类别 $i$ 的粒径分布函数 $N_i$ 的第 $r^{\text{th}}$ 阶矩的离散形式定义为：

$$M_r=\sum _{i=1}^{\infty }{i}^r{N}_i\text{\hspace{1em}(9.136)}$$

根据公式9.136（第402页），粒子群的总粒子数等于零阶矩：

$$N_t=\sum _{i=1}^{\infty }{N}_i=M_0=\text{ Total number of particles }$$

粒子的质量与其类别成正比；因此，粒子群体的总质量计算如下：

$$m_{p,t}=\sum _{i=1}^{\infty }{m}_{0}i{N}_i=m_0\sum _{i=1}^{\infty }{i}^1{N}_i=m_0{M}_1=\text{ Total mass of particles }$$

其中，$m_0$ 是一个常数，代表构成颗粒核心的体相物种分子的质量。

同样地，总颗粒体积可以通过以下方式获得：

$$v_{p,t}=\frac{m_0{M}_1}{{\rho }_b}$$

其中，${\rho }_b$ 表示颗粒核（烟灰密度）的体密度。

将公式 9.135（第 402 页）乘以烟灰颗粒尺寸类别 $i$，并利用公式 9.136（第 402 页）的表达式，我们得到：

$$\frac{d}{dt}\left[\sum _{i=1}^{\infty }{i}^r{N}_i\right]=\frac{d{M}_r}{dt}=G_r,\text{ for }r=0,1,2\dots \text{\hspace{1em}(9.137)}$$

其中，$G_r$ 是方程 9.135（第 402 页）的右侧，这是一个凝聚源项。

在炭黑形成过程中，除了凝聚过程外，成核和表面反应是另外两个重要的影响因素。在存在成核和表面反应的情况下，方程 9.137（第 403 页）可以写为：

$$\frac{d{M}_r}{dt}=R_r+G_r+W_r\text{\hspace{1em}(9.138)}$$

其中，$R_r$ 是成核源项，而 $W_r$ 是包括表面生长和氧化在内的表面反应的源项。

9.2.2.4.2 矩传输方程

方程 9.138（第 403 页）描述了由于单个点上各种子过程引起的矩的变化。在流动系统中，矩还会受到对流和扩散的影响。对于流动系统，烟灰浓度矩的传输方程可以写为：

$$\frac{\partial \left(\rho M_r\right)}{\partial t}+\nabla \cdot \left(\rho \overrightarrow{v}{M}_r\right)=\nabla \cdot \left(\frac{{\mu }_{eff}}{{\sigma }_t}\nabla M_r\right)+S_r\text{\hspace{1em}(9.139)}$$

其中

$M_r=r$ - 表示烟灰粒度分布的第 r 阶矩

${\mu }_{eff}=$ 有效扩散系数

${\sigma }_t=$ 用于矩传输方程的湍流普朗特数

$S_r=$ 使用方程 9.138（第 403 页）计算的矩传输中的源项

计算 $S_r$ 的源项将在后续章节中描述。

9.2.2.4.3 成核

在 Ansys Fluent 中，成核过程被模拟为两种烟灰前驱物种之间的凝聚。烟灰前驱体是一种用户定义的气相物种。通常，烟灰前驱体是多环芳烃（PAH），而烟灰核的形成被模拟为两个 PAH 分子的凝聚。PAH 的平均直径根据其中的碳原子数量和烟灰密度计算得出。PAH 的浓度从气相机理中获得。在许多实际情况下，模拟中使用的化学机理较小且不包括 PAH 物种，可以使用较小的物种，如 ${\mathrm{C}}_2{\mathrm{H}}_2$，作为 PAH 分子的构建基块，作为前驱物种。

第一阶矩的成核源项计算如下：

$$R_0=C_{nuc}\sqrt{T}{\left[Xp\right]}^2\text{\hspace{1em}(9.140)}$$

其中，$\left[Xp\right]$ 表示前驱物种的摩尔浓度，而 $C_{nuc}$ 是通过以下公式计算的常数：

$$C_{nuc}=\epsilon \sqrt{\frac{4\pi k_B}{m_c{N}_{C,P}}}{\left(d_P{N}_A\right)}^2\text{\hspace{1em}(9.141)}$$

其中

$\epsilon =2.2=\text{范德华增强因子}$

$k_B=\text{玻尔兹曼常数}$

$d_P=$ 前驱物种的直径

$N_{C,P}=$ 前驱分子中的碳原子数

$m_c=$ 碳原子的质量（12 amu）

$N_A=$ 阿伏伽德罗常数

基于动力学理论使用公式9.140（第404页）计算的成核速率通常非常大。为了适当地缩放它们，公式9.140（第404页）通过使用粘附系数$\gamma$进行了调整：

$$R_0=\gamma C_{\text{nuc }}\sqrt{T}{\left[Xp\right]}^2\text{\hspace{1em}(9.142)}$$

粘附系数的大小随前驱物种的尺寸（分子量）而变化。表9.4：不同多环芳烃（PAH）物种的粘附系数（第405页）列出了Blanquart和Pitsch[64]（第1060页）提出的不同前驱物种的粘附系数值。

表9.4：不同多环芳烃（PAH）物种的粘附系数

文献中还提出了其他建议，即采用与前驱体分子量的四次方成正比的黏附系数：

$${\gamma }_i=C_N{m}_i^4\text{\hspace{1em}(9.143)}$$

其中，$C_N$ 是一个常数，可以通过曲线拟合从表9.4：不同PAH物种的粘附系数（第405页）计算得出，或者从实验数据中获得。对于表9.4：不同PAH物种的粘附系数（第405页）中未列出的前驱体，可以使用方程9.143（第405页）来近似其粘附系数值。

另外，成核作用也可以被指定为两个前驱体之间的不可逆动力学反应。

$${\nu }_1{\mathrm{PAH}}_1+{\nu }_2{\mathrm{PAH}}_2\to \text{Soot+Products}\text{\hspace{1em}(9.144)}$$

$$R_0=A{T}^B\exp \left(-E/RT\right){\left[PA{H}_1\right]}^{{\eta }_1}{\left[PA{H}_2\right]}^{{\eta }_2}\text{\hspace{1em}(9.145)}$$

其中，$\eta$ 和 $v$ 分别是前驱物种的功率指数和化学计量系数。

公式 9.145（第 405 页）与公式 9.140（第 404 页）类似，包含相同的 PAH 物种，并且常数具有以下值：

$A=\gamma C_{\text{num }}$

$B=0.5$

$E=0$

${\eta }_1={\eta }_2=0.5$

$v_1=v_2=1$

更高阶矩的成核源项通过以下表达式从较低阶矩的源项计算得出：

$$R_r=2N_{C,P}{R}_{r-1},\text{ for }r>0\text{\hspace{1em}(9.146)}$$

9.2.2.4.4 凝并作用

一旦形成，烟灰颗粒会相互碰撞，影响烟灰颗粒群的尺寸分布。凝并过程假设形成的颗粒仍保持球形，但其直径增大。凝并过程改变了颗粒的数量密度，但不改变颗粒的总质量。由于凝并作用，动量输运方程中的源项计算如下：

$$G_0=-0.5\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{\beta }_{i,j}{N}_i{N}_j\text{\hspace{1em}(9.147)}$$

第二尺寸类别 $G_1$ 的凝结项等于0，因为凝结过程不会改变形成的总烟尘质量。

更高尺寸类别的凝结项通过以下方式计算：

$$G_r=0.5\sum _{k=1}^{r-1}\left(\frac{r}{k}\right)\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{i}^k{j}^{r-k}{\beta }_{i,j}{N}_i{N}_j\text{ for }r\ge 2\text{\hspace{1em}(9.148)}$$

其中，${\beta }_{i,j}$ 表示碰撞效率，该效率取决于凝并机制。

凝并过程可以在不同机制下发生：

• 连续介质机制

• 自由分子机制

• 介于两者之间的中间机制（或过渡机制）

凝并机制取决于努森数（Knudsen number）。

$$K_n=\lambda /d_s\text{\hspace{1em}(9.149)}$$

其中，$\lambda$ 表示气体混合物的平均自由程，而 $d_s$ 则代表煤烟颗粒的直径。煤烟颗粒的平均自由程 $\lambda$ 的计算方法如下：

$$\lambda =\frac{k_{B}T}{\sqrt{2}\pi d_{gas}^{2}P}\text{\hspace{1em}(9.150)}$$

其中，$k_B$ 是玻尔兹曼常数，$P$ 是压力，而 $d_{gas}$ 是通过计算得到的气体分子直径。

$$d_{\text{gas }}={\left(\frac{6M}{\rho \pi N_A}\right)}^{\frac{1}{3}}\text{\hspace{1em}(9.151)}$$

其中，$M$ 表示气体的分子量。

炭黑颗粒的平均直径 $d_s$ 根据方程 9.136（第 402 页）中炭黑矩的定义，按以下方式计算：

$$d_s=\frac{d_1\sum _{i=1}^{\infty }{i}^{1/3}{N}_i}{\sum _{i=1}^{\infty }{N}_i}=d_1\frac{M_{1/3}}{M_0}\text{\hspace{1em}(9.152)}$$

其中，$d_1$ 表示最小颗粒的直径，即单个碳原子。

针对不同的领域，求解方程 9.148（第 406 页）时会采用不同的处理方法，具体描述如下。

连续凝聚区 $\left(K_n<0.1\right)$

在连续区域中，碰撞系数表示为：

$${\beta }_{i,j}^c=K_C\left(\frac{C_i}{i^{1/3}}+\frac{C_j}{j^{1/3}}\right)\left(i^{1/3}+j^{1/3}\right)\text{\hspace{1em}(9.153)}$$

其中，$C_i$ 是坎宁安滑移修正因子，等于 $1+1.257\mathrm{Kn}$，$K_C$ 是连续介质碰撞因子，计算公式为：

$$K_C=\frac{2k_{B}T}{3\eta }$$

其中，$\eta$ 是混合物的分子粘度。

将碰撞系数（定义在第407页的公式9.153）代入第406页的公式9.148，得到如下所述的凝并引起的源项。

对于第一矩，连续凝并引起的矩源项为：

$$G_0^c=-K_c\left[M_0^2+M_{1/3}{M}_{-1/3}+K_c^{\prime }(M_{1/3}{M}_{-1/3}+M_{1/3}{M}_{2/3}\right]\text{\hspace{1em}(9.154)}$$

其中，$K_c^{\prime }=1.257\lambda /d_s$。

通过引入折算弯矩的概念，即${\mu }_r=M_r/M_0$，可以将第9.154公式（第407页）改写为：

$$G_0^c=-K_c\left[1+{\mu }_{1/3}{\mu }_{-1/3}+K_c^{\prime }({\mu }_{1/3}{\mu }_{-1/3}+{\mu }_{1/3}{\mu }_{2/3}\right]M_0^2\text{\hspace{1em}(9.155)}$$

同样地，对于 $r=2,3,\dots$，由于连续体凝结产生的矩源项可以表示为：

$$G_r^c=0.5K_c\sum _{k=1}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right)\left[\begin{array}{l}2{\mu }_k{\mu }_{r-k}+{\mu }_{k+1/3}{\mu }_{r-k-1/3}+{\mu }_{k-1/3}{\mu }_{r-k+1/3}+K_c\\ \left({\mu }_{k-1/3}{\mu }_{r-k}+{\mu }_k{\mu }_{r-k-1/3}+{\mu }_{k+1/3}{\mu }_{r-k-2/3}+{\mu }_{k-2/3}{\mu }_{r-k+1/3}\right)\end{array}\right]M_0^2\text{\hspace{1em}(9.156)}$$

方程9.155（第407页）和方程9.156（第407页）中的凝结项包括需要计算以实现封闭的分数阶矩以及负阶矩。这里采用了Frenklach（[192]（第1068页））提出的插值封闭过程。在插值封闭中，正分数阶矩通过多项式插值获得。由于后续矩的数值相差一个数量级，因此采用对数插值以最小化插值误差。分数矩通过以下表达式获得：

$$\log \left({\mu }_r\right)=L_{\text{Int }}\left(0,\log {\mu }_1,\log {\mu }_2,\log {\mu }_3,\dots \right)\text{\hspace{1em}(9.157)}$$

其中，$L_{Int}$ 是拉格朗日插值多项式。

为了计算负阶分数矩，采用了从整数阶矩进行外推的方法。

$$\log \left({\mu }_r\right)=L_{Ext}\left(0,\log {\mu }_1,\log {\mu }_2,\log {\mu }_3,\dots \right)\text{\hspace{1em}(9.158)}$$

其中，$L_{Ext}$ 是拉格朗日外推法。观察发现，对公式 9.157（第 408 页）进行二次插值，以及对公式 9.158（第 408 页）进行线性外推，效果相当不错。

自由分子区间的凝聚 $\left(K_n>10\right)$

在自由分子区间，碰撞系数计算如下：

$${\beta }_{i,j}^f=K_f\sqrt{\frac{i+j}{ij}}{\left(i^{1/3}+j^{1/3}\right)}^2\text{\hspace{1em}(9.159)}$$

其中，$K_f$ 是自由分子碰撞效率计算中的系数，具体形式如下：

$$K_f=\epsilon \sqrt{\frac{6k_{B}T}{{\rho }_s}}{\left(\frac{3m_c}{4\pi {\rho }_s}\right)}^{1/6}\text{\hspace{1em}(9.160)}$$

利用公式9.159（第408页）中的碰撞系数，公式9.155（第407页）和公式9.156（第407页）给出了自由分子区域中由于凝并产生的矩源项。

需要注意的是，以公式9.159（第408页）形式书写的碰撞系数是非加性的。因此，公式9.155（第407页）和公式9.156（第407页）现在表示为：

$$\begin{array}{rl}& G_0^f=-0.5K_f{M}_0^2{f}_{1/2}^{0,0}\\ & G_r^f=0.5K_f{M}_0^2\sum _{k=1}^{r-1}\left(\genfrac{}{}{0ex}{}{r}{k}\right)f_{1/2}^{r,r-k};r=2,3,\mathrm{4...}\end{array}\text{\hspace{1em}(9.161)}$$

其中，$f_l^{x,y}$ 是定义为的网格函数：

$$f_l^{x,y}=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{\left(i+j\right)}^l{i}^x{j}^y{\left(i^{1/3}+j^{1/3}\right)}^2{N}_i{N}_j\text{\hspace{1em}(9.162)}$$

由于对于 $l=1/2$ 时该表达式的评估并不直接，因此网格函数先对整数值的 $l$ 进行评估。随后，通过使用拉格朗日插值法获得分数值的网格函数。

例如，在解决三个矩的情况时，需要计算以下网格函数：

• 对于 $r=0$：$f_{1/2}^{0,0}$

• 对于 $r=1$：$f_{1/2}^{1,0}$，$f_{1/2}^{1,1}$

• 对于 $r=2$：$f_{1/2}^{2,0}$，$f_{1/2}^{2,1}$，$f_{1/2}^{1,2}$，$f_{1/2}^{2,2}$

这些函数首先通过计算 $f_0^{x,y}$，$f_1^{x,y}$ 和 $f_2^{x,y}$ 获得，然后应用拉格朗日插值法得到。

$$f_{1/2}^{x,y}=L\left(f_0^{x,y},f_1^{x,y},f_2^{x,y}\right)$$

请注意，网格函数具有对称性，即 $f_l^{x,y}=f_l^{y,x}$。

过渡区内的凝聚 $\left(0.1<K_n<10\right)$

当平均自由程与炭黑颗粒直径相当时，凝聚项的计算采用自由分子区和连续区之间的调和平均值，具体如下：

$$G_r^t=\frac{G_r^f{G}_r^c}{G_r^f+G_r^c}\text{\hspace{1em}(9.163)}$$

9.2.2.4.5 表面生长与氧化

一旦烟灰成核，气相中的碳会沉积在烟灰颗粒的表面，导致烟灰颗粒尺寸的增长以及烟灰质量的增加。由于成核形成的烟灰通常非常小。因此，烟灰表面的碳沉积是烟灰形成的主要模式。此外，烟灰颗粒会因${\mathrm{O}}_2$、$\mathrm{OH}$或其他氧化物种对烟灰表面的氧化而失去质量。表面生长和氧化过程受动力学控制且相当复杂。解析这些子过程的整个动力学涉及大型机制，因此计算成本高昂。然而，烟灰表面生长和氧化的过程可以通过使用小型机制（如单步全局机制）或简化机制来近似。

用于模拟表面生长和氧化的最广泛使用的机制之一是氢抽取${\mathrm{C}}_2{\mathrm{H}}_2$加成（HACA）机制。HACA机制通过仅涉及少数反应步骤的简化化学来表示表面生长和氧化的过程。

HACA机制有几种变体。在Ansys Fluent中用于模拟表面生长和氧化的HACA机制的Arrhenius速率参数如表9.5所示：HACA机制的Arrhenius速率参数（第410页）。

在表9.5：HACA机制的Arrhenius速率参数（第410页）中，前六个反应与表面生长有关，最后两个反应分别与${\mathrm{O}}_2$和OH引起的氧化有关。这些反应的反应速率取自Appel等人[22]（第1058页）。

表9.5：HACA机制的Arrhenius速率参数

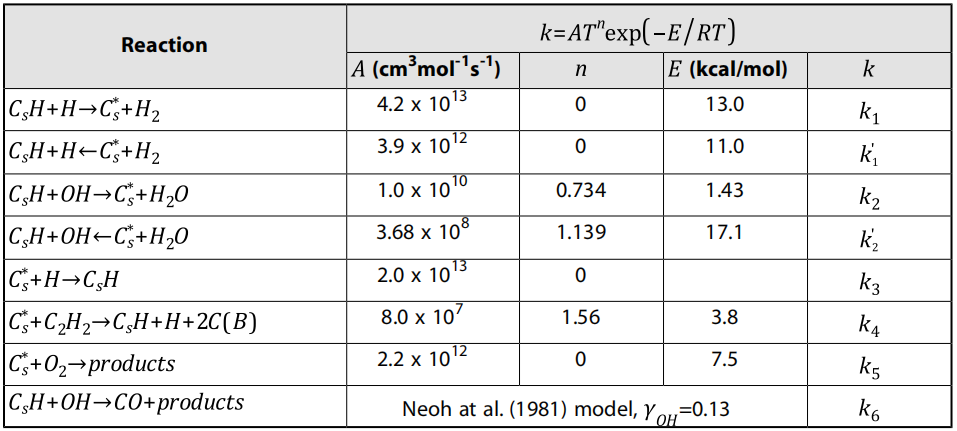
由于OH反应的氧化过程（表9.5中的反应6：HACA机制的阿伦尼乌斯速率参数，第410页）涉及气相物种与表面物种之间的碰撞，因此反应速率常数以粘附系数（反应概率）${\gamma }_i$的形式指定。

粘附系数的“类阿伦尼乌斯”无单位形式被定义为一个概率，其中计算值大于1的被设定为1：

$${\gamma }_i=\min \left(1,a_i{T}^{b_i}\exp \left(\frac{-c_i}{RT}\right)\right)\text{\hspace{1em}(9.164)}$$

通过气体物种与体相物种的碰撞频率，将粘附系数转换为质量作用动力学速率常数：

$$k_{f_i}={\gamma }_i\frac{\prod _{i=1}^{N_{i=1}^{v_{ji}^{v_{ji}^{v_{ji}}}}}}{{\Gamma }_t^m}\sqrt{\frac{RT}{2\pi W_k}}\text{\hspace{1em}(9.165)}$$

其中，

$W_k=$ 气相物种的分子量

${\Gamma }_t=$ 总表面位点浓度的总和

$m=$ 反应表面物种的化学计量系数的总和

${\sigma }_j=$ 表面物种的占据率

$v_{ji}^{\prime }=$ 表面物种的反应级数

在公式9.165（第410页）中，项${\Gamma }_t^m$ 用于将无量纲的粘附系数转换为速率常数的适当单位。气相/表面碰撞频率由项$\sqrt{\frac{RT}{2\pi W_k}}$ 考虑。如果所有物种的占据率为1，则生成项$\prod _{i=1}{\sigma }_j^{v_{ji}^{\prime }}$ 等于1。

表面反应很快。活性自由基位点的浓度处于稳态。活性自由基位点的浓度可以用活性位点的一部分来表示：

$$\frac{C_s^{\ast }}{C_{s}H}=A=\frac{k_1\left[H\right]+k_2\left[OH\right]+k_6\left[OH\right]}{k_1^{\prime }\left[H_2\right]+k_2^{\prime }\left[H_{2}O\right]+k_3\left[H\right]+k_4\left[C_2{H}_2\right]+k_5\left[O_2\right]}\text{\hspace{1em}(9.166)}$$

炭黑表面活性位点的浓度为 $\chi {\mathcal{C}}_{s}H$。炭黑表面总的活性位点数量近似为：

$$C_{\chi ,\text{ soot }}=\frac{{\chi }_s}{N_A}\alpha S\text{\hspace{1em}(9.167)}$$

其中

$\alpha =\tanh \left(a/\log {\mu }_1+b\right)=\text{活性位点分数}$

$a=12.65-56.3{\mathrm{e}}^{-4}\mathrm{T}$

$b=-1.38+6.8{\mathrm{e}}^{-4}\mathrm{T}$

${\chi }_s=\text{位点数量}$

$S=\text{表面密度}\left(1/\mathrm{m}\right)$

活性自由基位点计算如下：

$$C_s^{\ast }=\alpha {\chi }_s\pi d_1^2\frac{A}{A+1}\text{\hspace{1em}(9.168)}$$

其中，$d_1$ 代表碳原子的直径。

表面生长反应和氧化过程的力矩源项计算方法如下：

• 由于乙炔（${\mathrm{C}}_2{\mathrm{H}}_2$）的添加引起的表面生长：

$$W_r^{C_2{H}_2}=k_4\left[C_s^{\ast }\right]\left[C_2{H}_2\right]M_0\sum _{k=0}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right){\left(\Delta \right)}^{r-k}{\mu }_{k+2/3}\text{\hspace{1em}(9.169)}$$

• 由于存在 ${\mathrm{O}}_2$ 引起的氧化：

$$W_r^{O2}=k_5\left[C_s^{\ast }\right]\left[O_2\right]M_0\sum _{k=0}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right){\left(-\Delta \right)}^{r-k}{\mu }_{k+2/3}\text{\hspace{1em}(9.170)}$$

由于$\mathrm{OH}$沉积导致的表面增长：

$$W_r^{OH}=k_6\left[C_{S}H\right]\left[OH\right]M_0\sum _{k=0}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right){\left(-\Delta \right)}^{r-k}{\mu }_{k+2/3}\text{\hspace{1em}(9.171)}$$

在公式9.169（第411页）至公式9.171（第411页）中，$\Delta$表示被移除或添加的碳原子数量：

• 对于由于${\mathrm{O}}_2$引起的表面生长和氧化，$\Delta =2$

• 对于由于$\mathrm{OH}$引起的表面生长和氧化，$\Delta =1$

对于第$r$阶矩，由于表面生长和氧化产生的总源项为

$$W_r=W_r^{C_2{H}_2}+W_r^{O_2}+W_r^{OH}\text{\hspace{1em}(9.172)}$$

请注意，在HACA机制下，乙炔在炭黑表面生长过程中被消耗。由于Ansys Fluent在求解之前生成火焰面，火焰面对炭黑过程一无所知，这可能导致非预混/部分预混燃烧模型对炭黑表面生长的过度预测，最终导致更高的炭黑产率。

9.2.2.4.6 炭黑聚集

在凝聚（第406页）中，炭黑颗粒的凝聚假设为聚结生长，即两个较小颗粒碰撞形成的大颗粒总是球形的。然而，在许多实际燃烧设备中，炭黑的生长可能不仅限于聚结状态。碰撞的颗粒可以粘附在一起，形成称为聚集体的链状结构。聚集体的表面积比相同质量的聚结单个球体大。因此，聚集体的形成增强了凝聚过程的速率。忽视聚集体的形成可能导致凝聚和炭黑表面生长速率计算中的误差。

在聚集体碰撞状态下，炭黑颗粒大小分布变为二元分布。聚集体内初级颗粒的数量代表内部坐标，而聚集体的质量和大小代表外部坐标。解析二维PDF并非易事，且计算成本高昂。Ansys Fluent采用了Kazakov和Frenklach [298]（第1074页）提出的方法，该方法将用于建模炭黑形成的矩方法扩展到考虑炭黑聚集。当前的公式区分了两种凝聚状态，即聚结和聚集，根据用户指定的临界直径在两者之间切换。如果平均颗粒直径小于临界直径，则假设凝聚为聚结。当炭黑颗粒直径达到临界值时，凝聚自动切换到聚集状态。

在存在团聚过程的情况下，方程9.136（第402页）至方程9.139（第403页）描述了烟灰团聚体的粒径分布及其质量输运（即浓度矩）。除了团聚体的矩之外，类似于方程9.136（第402页），团聚体中初级粒子的分布的浓度矩的离散形式定义如下：

$${}^P{M}_r=\sum _{i=1}^{\infty }{n}_i^r{N}_i\text{\hspace{1em}(9.173)}$$

其中，${}^P{M}_r$ 表示颗粒的第 $r$ 阶矩，而 $n_i^r$ 则代表第 $i$ 类中的初级颗粒数量。类似于聚合质量（或全局）矩的概念，此处同样可以采用归一化颗粒矩的概念：

$${\theta }_r=\frac{{}^P{M}_r}{{}^P{M}_0}\text{\hspace{1em}(9.174)}$$

其中，${\theta }_r$ 表示聚集体内初级颗粒的第 $r$ 阶简化矩。

根据第 402 页的公式 9.136 和第 412 页的公式 9.173 的定义，颗粒零阶矩 ${}^P{M}_0$ 与全局零阶矩 $M_0$ 是相同的，即：

$${}^P{M}_0=M_0\text{\hspace{1em}(9.175)}$$

此外，一个聚集体中粒子的平均数量 $n_p$ 可以通过前两个矩来表示，具体如下：

$$\left(n_p\right)={\theta }_1=\frac{{}^P{M}_1}{{}^P{M}_0}\text{\hspace{1em}(9.176)}$$

类似于总量的矩，颗粒的矩也会因为各种炭黑生成子步骤（如成核和凝聚）以及颗粒在物理空间中的迁移而发生变化。描述颗粒矩变化的控制方程可以写为：

$$\frac{d^P{M}_r}{dt}=R_0+H_r,r=1,2,3\dots \text{\hspace{1em}(9.177)}$$

其中，

$R_0=\text{由公式9.140（第404页）计算的成核源项}$

$H_r=\text{由于聚集体凝结产生的源项}$

因为公式9.175（第413页）已经给出了$r=0$的解，所以公式9.177（第413页）仅在$r>0$时求解。

第一颗粒矩${}^P{M}_1$给出了初级颗粒的平均数量$n_p$（公式9.176（第413页）），从中可以计算颗粒质量。$H_1=0$，因为颗粒总质量不会因凝结过程而改变。

对于更高的矩，公式9.177（第413页）中的$H_r$需要计算。利用公式9.148（第406页）以及公式9.173（第412页）中颗粒矩的定义，$H_r$可以表示为

$$H_r=0.5\sum _{k=1}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right)\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{n}_i^k{n}_j^{r-k}{\beta }_{i,j}{N}_i{N}_j,\text{ for }r\ge 2\text{\hspace{1em}(9.178)}$$

其中，$\beta$ 是总的碰撞系数。其数值取决于碰撞状态，

该状态通过克努森数 $K_n$（公式 9.149，第 406 页）计算得出。

连续介质状态下的聚集体凝聚作用 $\left(K_n<0.1\right)$

在连续介质状态下，聚集体的碰撞系数表示为：

$${}^a{\beta }_{i,j}={}^a{\beta }_{i,j}^c=K_C\left(\frac{C_i}{d_i}+\frac{C_j}{d_j}\right)\left(d_i+d_j\right)\text{\hspace{1em}(9.179)}$$

其中，$d_i$和$d_j$分别表示不同尺寸类别$i$和$j$的团聚体的碰撞直径。其余符号与公式Equation 9.153（第407页）中的相同。对于凝聚碰撞，假设碰撞直径和颗粒直径相同。然而，由于团聚作用，碰撞直径可能与颗粒直径有显著差异，这取决于团聚体的分形结构。一个团聚体由若干个

初级颗粒组成，这些初级颗粒被假设为球形且尺寸相同。团聚体的碰撞直径通过以下关系计算：

$$d=d_p{n}_p^{1/F}\text{\hspace{1em}(9.180)}$$

其中，$d_p$ 表示初级粒子的直径，而 $F$ 是描述团聚体分形结构的分数维数。文献中建议，团聚体凝并过程中，$F$ 的取值在 1.7 至 2.0 之间较为合理。在纯粹的聚结凝并过程中，$F=3$。团聚体的质量可通过以下方式指定：

$$m=n_p\left(\frac{\pi }{6}\rho d_p^3\right)\text{\hspace{1em}(9.181)}$$

从公式9.180（第414页）和公式9.181（第414页）中，我们可以将总碰撞直径表示为：

$$d={\left(\frac{6}{\rho \pi }m\right)}^{1/3}{n}_p^{\left(1/F-1/3\right)}\text{\hspace{1em}(9.182)}$$

将碰撞直径的值从公式9.182（第414页）代入公式9.179（第413页），并替换公式9.178（第413页）中的碰撞系数值，我们得到第$r^{\text{th}}$阶矩的总凝聚源项：

$$H_r^c=0.5K_c\sum _{k=1}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right)\left[\begin{array}{l}2{\theta }_k{\theta }_{r-k}+⟨m_i^{1/3}{n}_i^{k+\phi }⟩⟨m_j^{-1/3}{n}_j^{r-k-\phi }⟩+⟨m_i^{-1/3}{n}_i^{k-\phi }⟩⟨m_j^{1/3}{n}_j^{r-k+\phi }⟩\\ +K_c\left(\begin{array}{l}⟨m_i^{-1/3}{n}_i^{k-\phi }⟩{\theta }_{r-k}+⟨m_j^{-1/3}{n}_i^{r-k-\phi }⟩{\theta }_k+⟨m_i^{1/3}{n}_i^{k+\phi }⟩⟨m_j^{-2/3}{n}_j^{r-k-2\phi }⟩+\\ ⟨m_i^{-2/3}{n}_i^{k-2\phi }⟩⟨m_j^{1/3}{n}_j^{r-k+\phi }⟩\end{array}\right)\end{array}\right]\text{\hspace{1em}(9.183)}$$

哪里，

$$\phi =\frac{1}{F}-\frac{1}{3}\text{\hspace{1em}(9.184)}$$

方程9.183（第414页）涉及了炭黑聚集体尺寸及其初级粒子数量的二元矩。二元矩的计算并非易事，需要粒径分布的多维概率密度函数（PDF）。Kazakov和Frenklach [298]（第1074页）提出了一种近似方法，即利用两个一维矩来逼近二元矩，具体如下：

$$⟨m^x{n}^y⟩\approx ⟨m^x⟩⟨n^y⟩={\mu }_x{\theta }_y\text{\hspace{1em}(9.185)}$$

因此，方程9.183（第414页）可以写作：

$$H_r^c=0.5K_c\sum _{k=1}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right)\left[\begin{array}{l}2{\theta }_k{\theta }_{r-k}+{\mu }_{1/3}{\theta }_{k+\phi }{\mu }_{-1/3}{\theta }_{r-k-\phi }+{\mu }_{-1/3}{\theta }_{k+\phi }{\mu }_{1/3}{\theta }_{r-k+\phi }\\ +K_c\left\{\begin{array}{l}{\mu }_{-1/3}{\theta }_{k-\phi }{\theta }_{r-k}+{\mu }_{-1/3}{\theta }_{r-k-\phi }{\theta }_k+{\mu }_{1/3}{\theta }_{k+\phi }{\mu }_{-2/3}{\theta }_{r-k-2\phi }+\\ {\mu }_{-2/3}{\theta }_{k-2\phi }{\mu }_{1/3}{\theta }_{r-k+\phi }\end{array}\right\}{M}_0^2\end{array}\right]\text{\hspace{1em}(9.186)}$$

方程9.186（第414页）包含了分数和中间初级粒子的矩，这些矩是使用与聚合矩相同的插值方法计算的（参见方程9.157（第408页）和方程9.158（第408页））。

自由分子区域中的聚合凝并$\left(K_n>10\right)$

在自由分子区域中，碰撞系数可以表示为：

$${}^a{\beta }_{i,j}^f=K_f\sqrt{\frac{m_i+m_j}{m_i{m}_j}}{\left(d_i+d_j\right)}^2\text{\hspace{1em}(9.187)}$$

其中，$m$ 和 $d$ 分别表示聚集体的质量和碰撞直径。碰撞直径是通过公式 9.182（第 414 页）计算得出的。与自由分子区凝聚计算中的聚结凝聚类似，由于公式 9.187（第 415 页）中的非加性碰撞系数项，计算因聚集体凝聚而产生的源项 $H_r$（公式 9.178，第 413 页）时会遇到困难。类似于公式 9.161（第 408 页）的方式，$H_r$ 可以表示为：

$$H_r^f=0.5K_f{M}_0^2\sum _{k=1}^{r-1}\left(\begin{array}{l}r\\ k\end{array}\right)h_{1/2}^{r,r-k};r=2,3,4\dots \text{\hspace{1em}(9.188)}$$

其中，$h_{1/2}$ 表示聚合网格函数。将公式 9.178（第413页）和公式 9.188（第415页）的右侧等式相等，并代入公式 9.187（第415页）中的碰撞系数，聚合网格函数可以表示为：

$$h_l^{x,y}=\frac{1}{M_0^2}\left(\sum _{q=0}^l\left(\begin{array}{l}l\\ q\end{array}\right)\left(\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{m}_i^q{m}_j^{l-q}{m}_i^{1/2}{m}_j^{1/2}{\left(d_i^{1/3}+d_j^{1/3}\right)}^2{n}_i^x{n}_j^y{N}_i{N}_j\right)\right)\text{\hspace{1em}(9.189)}$$