12.9.1 简介
Ansys Fluent 针对模拟液体液滴撞击壁面并形成薄膜的过程,提供了一种特定的边界条件。该模型特别适用于内燃机的模拟。Lagrangian 壁面薄膜模型采用瞬态 Lagrangian 粒子来离散物理效应,因此非常适合快速瞬态效应。此外,还存在一种能够处理稳定壁面薄膜的 Eulerian 壁面薄膜模型(Eulerian 壁面薄膜(第837页))。
喷雾与壁面相互作用是进气道燃油喷射(PFI)发动机混合物形成过程中的重要环节。燃油喷雾撞击表面,通常在进气门附近的进气道以及进气门本身,液滴在此处溅射并随后蒸发。蒸发的混合物被卷入发动机气缸,与新鲜充气和气缸内的任何残留气体混合。被压缩和燃烧的混合物最终通过排气口排出。这一过程每分钟重复200至8000次,具体取决于发动机。
由于壁面上形成了油膜,进气道中仍残留着几个周期的燃油。这使得油膜对于进气道燃油喷射(PFI)发动机的碳氢化合物排放变得重要起来。此外,直喷式(DI)发动机的燃烧室内也可能形成油膜。在直喷发动机中,燃油直接喷入燃烧室,如果喷射事件发生在循环的早期或晚期,喷雾可能会撞击活塞。直喷发动机内壁面油膜的建模,尤其是在柴油发动机中,由于发动机表面存在积碳而变得复杂。这些积碳在撞击时会吸收液态油膜。人们认为积碳会在循环后期吸附燃油,然而这一现象非常复杂,尚未被充分理解。
此外,壁面油膜的形成是选择性催化还原(SCR)后处理过程的一个重要因素。利用氨对氮氧化物进行选择性催化还原是一项成熟的技术,用于满足全球严格的氮氧化物(NOx)排放标准。SCR系统设计者面临多项技术挑战,如氨滑脱、尿素结晶、低温沉积以及其他潜在问题。如果不将壁面油膜形成的物理过程纳入SCR预测模型,可能会在NOx转化预测中引入较大误差。
最后,壁面油膜建模在燃气轮机运行和电子设备冷却中也扮演着重要角色。
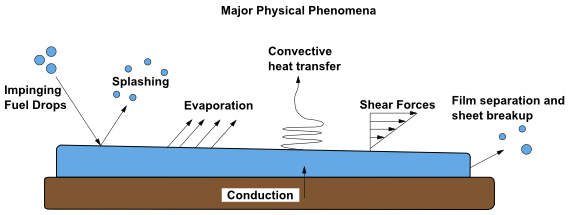
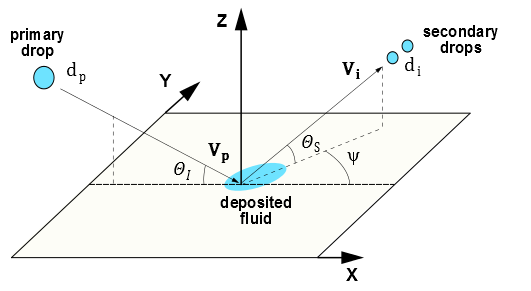
DPM粒子用于模拟壁面薄膜。Ansys Fluent中的壁面薄膜模型允许液滴撞击边界表面并形成薄膜。该模型可以细分为四个主要子主题:与壁面边界初始撞击时的相互作用、随后在表面上的追踪、薄膜变量的计算以及与气相的耦合。图12.7:拉格朗日壁面薄膜的溅射、动量、热和质量传递机制(第498页)示意性地展示了拉格朗日壁面薄膜模型考虑的基本机制。
图12.7:拉格朗日壁面薄膜的溅射、动量、热和质量传递机制
拉格朗日壁面薄膜模型的主要假设和限制如下:
-
薄膜层很薄,厚度小于500微米。这一限制是由于薄膜中线性速度分布的假设。
-
薄膜粒子的温度变化相对缓慢,因此可以利用解析积分方案。
-
假设薄膜粒子直接接触壁面表面,壁面到薄膜的热传递通过传导进行。
-
薄膜温度永远不会超过液体的沸腾温度。
如果你想模拟喷雾撞击非常热的壁面,壁面射流模型可能更合适,因为在壁面射流撞击模型中,假设液滴下方存在一层蒸汽层,使它们无法直接接触边界表面。对于典型操作条件下的柴油发动机计算,这可能是一个更准确的假设。
有关在Ansys Fluent中使用拉格朗日壁面薄膜模型的更多信息,请参阅《Fluent用户指南》中的“拉格朗日壁面薄膜建模”。
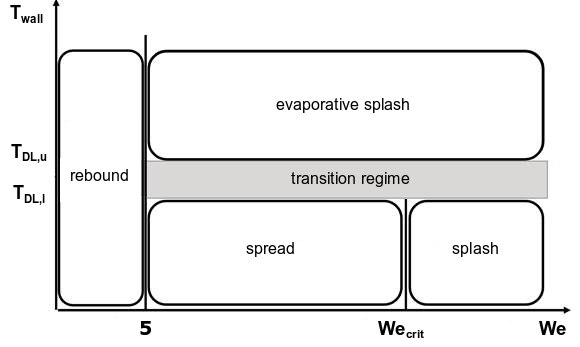
12.9.2 莱顿弗罗斯特温度考虑因素
在拉格朗日壁膜(LWF)模型中,壁膜蒸发速率方程(扩散控制模型的方程12.275(第519页),对流-扩散控制模型的方程12.282(第520页),以及壁膜边界层模型的方程12.291(第523页)和方程12.292(第523页))假设液体膜完全接触壁面。当壁膜温度达到沸点时,计算沸点速率;然而,假设仍然是液体膜完全覆盖壁面。
LWF沸点速率方程(恒温壁和热流壁分别为方程12.283(第520页)和方程12.284(第521页))给出了沸点速率对壁温的线性依赖关系。然而,液体膜沸点现象要复杂得多,随着壁面与液体膜之间的温度差增加,从热壁到膜的热传递速率偏离线性依赖关系。这种偏离是由在热壁表面和沸点膜之间形成的蒸汽口袋引起的,这显著影响了膜沸点过程的热传递和流体动力学特性。绝热蒸汽层完全覆盖热壁的极限条件被称为莱顿弗罗斯特点。
Fluent在多相模型背景下处理壁面沸点现象,特别是在壁面沸点模型(第733页)中。然而,在LWF模型的背景下,预测莱顿弗罗斯特点对于评估LWF沸点速率的充分性并避免非物理结果至关重要。
12.9.2.1 默认壁温限制器
在Ansys Fluent中,默认的壁面温度限制是液膜沸点与壁面和液膜之间温度差之和:
默认的 为 。
12.9.2.2 莱顿弗罗斯特温度报告
在进行LWF计算过程中,Ansys Fluent会计算莱顿弗罗斯特温度并将其与壁面温度进行比较。如果壁面温度高于莱顿弗罗斯特温度,Fluent会发出警告。需要注意的是,莱顿弗罗斯特点的计算仅用于信息提示,并不用于限制计算中的壁面温度。
对于等温表面,莱顿弗罗斯特温度 可以近似为液体临界温度 和液体表面张力 的函数 [51](第1059页):
其中, 表示固体的密度, 是固体的原子序数。方程 12.206(第 500 页)中的最后一项引入了对固-液表面张力效应的修正。
了解 以及固体表面的传热特性后,莱顿弗罗斯特温度 可按以下公式计算:
其中, 表示液膜温度(K),erfc 是互补误差函数,
其中:
固体导热系数
固体密度
固体比热容
12.9.3 边界撞击期间的相互作用
预测液滴与墙壁的撞击并不直接,因为涉及大量参数。任何撞击的结果都由液滴液体(粘度、表面张力、密度)和撞击条件(液滴直径和液滴速度)的性质决定。另外两个对撞击结果有重要贡献的因素是表面粗糙度和表面液膜的厚度。此外,墙壁温度也可能影响撞击动力学。
有几种模型可以描述撞击物理过程并预测撞击结果。Ansys Fluent 提供了以下模型:
-
Stanton 和 Rutland 模型 [629] (p. 1093), [631] (p. 1093) 使用墙壁温度和基于韦伯数的准则来定义撞击状态(粘附、反弹、扩散和飞溅)之间的固定值阈值。在 Fluent 实现中,原始的 Stanton-Rutland 模型已通过 O'Rourke 和 Amsden [495] (p. 1086) 的概念进行了扩展。更多详情请参见 Stanton-Rutland 模型 (p. 501)。
-
Kuhnke 模型 [324] (p. 1076) 考虑了干燥和湿润的墙壁,并额外考虑了液滴属性和撞击条件、表面粗糙度和膜厚度的影响。Kuhnke 模型区分以下状态:反弹、扩散、飞溅和干燥飞溅(热破碎)。更多信息请参见 Kuhnke 模型 (p. 508)。
-
Stochastic Kuhnke 模型 [606] (p. 1092), [37] (p. 1059) 源自 Kuhnke 模型,具有以下特点:
-
使用为选择性催化还原(SCR)建模应用开发和调整的不同状态转换准则。
-
在关键温度转换过程中引入随机效应。
-
引入了蒸发溅射机制,采用“部分蒸发”概念,即在特定条件下假设部分撞击液滴完全蒸发。
详情参见随机Kuhnke模型(第514页)。
- 用户自定义的撞击模型可通过使用DEFINE_IMPINGEMENT、DEFINE_FILM_REGIME和DEFINE_SPLASHING_DISTRIBUTION用户自定义函数来实现,具体描述见Fluent用户指南和Fluent定制手册中的用户自定义函数部分。
注意:
-
对于能量方程未求解的情况,拉格朗日壁面薄膜模型适用,其撞击/溅射模型基于以下假设:
-
壁面温度为
-
液膜的饱和温度等于
-
后续章节中提及的颗粒速度相对于壁面坐标系。除非另有说明,无量纲参数和基于垂直于壁面的颗粒速度。
12.9.3.1 Stanton-Rutland模型
12.9.3.1.1 机制定义
壁面相互作用基于Stanton [629](第1093页)和O’Rourke [496](第1086页)的工作,根据局部信息计算液滴与壁面相互作用的机制。四种机制(粘附、反弹、扩散和溅射)基于撞击能量和壁面温度。以下图表有助于展示界限。
图12.8:壁面相互作用准则的简化决策图
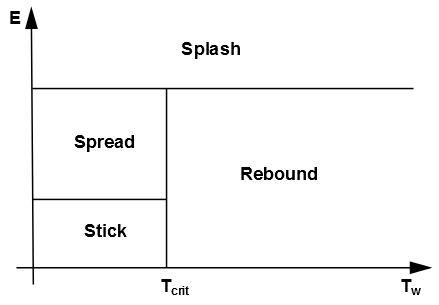
低于液体的临界转变温度时,撞击液滴可能粘附、扩散或溅射;高于临界转变温度时,颗粒可能反弹或溅射。
机制划分的标准基于撞击能量和液体的临界转变温度。撞击能量定义为...
其中, 表示粒子垂直于壁面的速度, 是液体密度, 是液滴直径, 是液体表面张力, 是液膜高度。这里, 表示边界层厚度,其定义为
雷诺数定义为 。通过如第12.208式(第502页)那样定义能量,壁面上薄膜的存在抑制了飞溅现象,但当薄膜高度趋近于零时,并不会产生非物理结果。
临界过渡温度定义为:
其中, 表示饱和温度,而 是临界温度因子,其值根据应用场景在1至1.5之间变化。 的默认值为1;因此,默认的临界转变温度 将等于液滴的饱和温度 。
作为拉格朗日壁面薄膜模型的替代方案,临界转变温度 可以通过在液体饱和温度 上增加一个恒定偏移量 来计算:
当无量纲能量 小于 16 时,应用附着状态,此时颗粒速度设定为壁面速度。在扩散状态中,颗粒的初始方向和速度根据壁面射流模型设定,其中液滴沿表面特定方向的概率通过与无粘性液体射流的类比给出,该射流的动量通量具有经验定义的径向依赖性。
如果壁面温度高于液体的临界转变温度,低于临界冲击能量 的冲击事件会导致颗粒从壁面反弹。
当冲击能量超过一个临界能量阈值,定义为 =57.7 时,会发生溅射。溅射液滴包的数量在 Wall 边界条件对话框中设定,默认数量为 4,但您可以选择 0 到 10 之间的数字。溅射算法遵循 Stanton [629](第 1093 页)的描述,并在溅射(第 503 页)中详细说明。
12.9.3.1.2 反弹
在反弹状态中,反弹颗粒的速度由以下公式给出:
其中, 和 分别是反弹速度的切向和法向分量, 是冲击速度的切向分量,而 则是由以下公式给出的法向恢复系数:
是从壁面测量的冲击角度,以弧度为单位。
反弹粒子的偏转角 在入射方向的 -90° 到 90° 之间随机取值。
12.9.3.1.3 飞溅
图 12.9:Stanton-Rutland 模型:冲击与飞溅(第 504 页)图形化地描述了 Stanton-Rutland 飞溅模型中的以下飞溅液滴变量。
-
冲击粒子的直径,
-
冲击粒子的速度, 及其变化性
-
飞溅的二次粒子的直径,
-
飞溅的二次粒子的速度,
-
从壁面法线测量的冲击角度
-
从壁面法线测量的飞溅粒子的反射角
-
从入射方向的偏转角
图 12.9:Stanton-Rutland 模型:冲击与飞溅
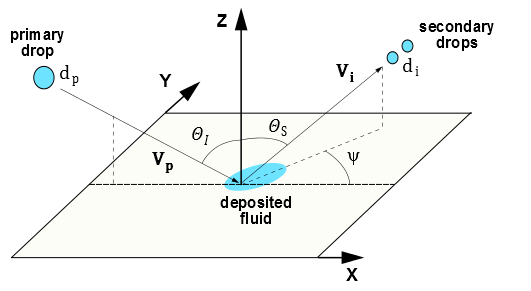
如果冲击表面的粒子具有足够高的能量,粒子会发生飞溅并产生多个新粒子。您可以在 DPM 标签或 Wall Film 标签的 Wall 边界条件对话框中明确设置每次冲击产生的粒子数量。飞溅包的最小数量为三个。飞溅包的属性(直径、大小和方向)从以下章节描述的实验获得的分布函数中随机抽样。在拉格朗日壁膜模型中将飞溅包的数量设置为零会关闭拉格朗日模型的飞溅计算。请记住,每个飞溅包可以被视为分布曲线的离散样本,并且在 Wall 边界条件对话框中选择飞溅液滴的数量并不限制飞溅液滴的数量,只是代表这些液滴的包的数量。
因此,对于每个溅射的包裹,通过从累积概率分布函数(CPDF)中采样,也称为F,该函数来自威布尔分布函数,并根据Mundo等人[465](第1084页)的数据进行拟合,从而获得不同的直径。方程为
该分布代表了在飞溅液滴样本中找到直径为 的液滴的概率。此分布与 O’Rourke [496](第1086页)所使用的 Nakamura-Tanasawa 分布函数相似,其分布参数 。为确保分布函数在韦伯数增加时产生符合物理规律的结果,采用了 O’Rourke [496](第1086页)提供的以下 表达式。飞溅尺寸分布峰值处的粒径与撞击粒径的比值由下式给出:
能量表达式由方程12.208(第502页)给出。低韦伯数冲击由方程12.216(第504页)中的第二项描述,并且在O’Rourke [496](第1086页)分析的任何实验中,对于极高能量冲击,飞溅峰值直径比绝不会小于0.06。方程12.216(第504页)中的韦伯数是使用粒子法向速度和直径定义的:
累积概率分布函数(CPDF)是必需的,以便能够从实验数据中采样直径。通过积分公式12.215(第504页)可以得到CPDF。
其范围在零和一之间。通过反转公式12.218(第505页)并在零和一之间采样CPDF,得到了直径的表达式(该直径是撞击韦伯数和撞击能量的函数)。因此,第个溅射液滴包的直径表达式为,其中是第个随机样本。一旦确定了溅射液滴的直径,通过在给定直径处评估公式12.215(第504页),就可以确定在该样本中找到该液滴的概率。
为了防止溅射颗粒直径变得过大,Ansys Fluent采用了分布限制方法:
- 尾部限制方法(拉格朗日壁膜模型的默认设置)限制了
其中, 表示粒径,对应于累积概率密度函数(CPDF)的 处。
- 峰值限制法(欧拉壁膜模型的默认设置)限制了粒径比。
其中, 是一个限制值,根据 Mundo [465](第1084页)从实验数据中确定的范围为0.2到0.3(默认值为0.22)。
可以通过文本用户界面(TUI)命令选择限制方法和参数 。
每个包裹中的液滴数量与该液滴大小的PDF值成正比。然后,总粒子数由溅射的总质量决定。
溅射粒子的质量分数 是从Yarin和Weiss [724](第1099页)的实验数据中获得的。O’Rourke等人 [496](第1086页)给出的溅射质量分数表达式为:
Stanton等人[629](第1093页)提出的飞溅质量分数表达式如下:
其中, 是无量纲冲击速度,定义为:
其中, 由公式 12.236(第 508 页)定义,常数 取值为 2.37。
飞溅质量分数方法可通过 TUI 命令选择,对于拉格朗日壁面薄膜(LWF),默认采用 O’Rourke 表达式;对于欧拉壁面薄膜(EWF),默认采用 Stanton 表达式。
作者(O’Rourke 等人[496](第 1086 页))指出,对于典型的柴油喷雾,几乎所有撞击都远高于上限,因此飞溅事件几乎总是会弹出撞击液滴质量的 75%。为了得到液滴总数量的表达式,我们注意到质量守恒要求飞溅包裹的总质量之和必须等于飞溅质量分数,即
其中,表示撞击气块的总质量。总溅射液滴数量的表达式为
每个包裹溅射出的液滴数量由 乘以该液滴尺寸对应的概率密度函数(PDF)值来确定。
为了计算溅射液滴离开表面的速度,还需对速度的法向分量进行额外的相关性采样。采用拟合Mundo [465](第1084页)数据的高斯威布尔函数作为法向分量的概率密度函数(PDF)。概率密度表示为
其中,索引 指的是第 个溅射的液滴,而下标 指的是撞击的液滴。 和 是 的函数, 是从表面法线测量的撞击角度:
速度的切向分量是通过反射角表达式 获得的:
结合
请注意,反射角 是从表面法线测量的,并且 和 都以度为单位。
根据 [630](第 1093 页)的计算,飞溅液滴的方位角 假设遵循分布 (公式 12.227,第 507 页)。该处理基于 Naber 和 Reitz [468](第 1084 页)开发的方法。
其中, 是一个与冲击角度 相关的参数,其关系为:
是通过对公式12.227(第507页)和公式12.228(第507页)进行积分来确定的,具体如下:
- 对于 的情况:
对于 的情况:
在上式中, 是一个在0到1之间均匀分布的随机数。
最后,对新形成的微粒进行能量平衡计算,以确保新水滴的动能和表面能之和不超过旧水滴的能量总和。能量平衡的计算公式如下:
其中, 是发生溅射的阈值能量。为了确保能量守恒,计算以下修正因子:
阈值能量 计算如下:
其中, 表示从临界韦伯数计算得出的溅射阈值速度。
临界韦伯数则由以下公式给出:
由于飞溅液滴速度的采样点数量相对较少,因此需要这一修正因子(详见Stanton [631](第1093页))。在方程12.232(第507页)中,飞溅包的各组成部分乘以的平方根,以确保能量守恒。因此,飞溅包的法向和切向速度分量可表示为:
需要注意的是,飞溅事件本质上是瞬态的,因此飞溅子模型仅在 Ansys Fluent 中进行非稳态追踪时可用。飞溅还可能导致发生飞溅的单元中的源项大幅增加,这可能会导致时间步长之间收敛困难。因此,在启用飞溅功能进行模拟时,可能需要使用更小的时间步长。
12.9.3.2 Kuhnke 模型
12.9.3.2.1 状态定义
图 12.10:Kuhnke 冲击模型状态(第 508 页)展示了 Kuhnke [324](第 1076 页)冲击模型的冲击图。该模型通过基于无量纲变量 和 将相关冲击现象分类为四种状态,考虑了所有相关的冲击现象:扩散(或沉积)、反弹、飞溅和干燥飞溅(热破碎)。沉积和飞溅状态会导致壁膜的形成。
图 12.10:Kuhnke 冲击模型状态
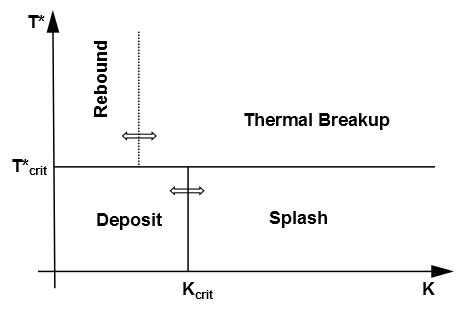
无量纲变量 定义为:
其中:
无量纲变量 定义如下:
在上述方程中,使用了以下符号表示:
基于法向冲击速度的韦伯数
拉普拉斯数
液滴密度
液滴直径
法向冲击速度
液滴表面张力
液滴粘度
壁面温度 (K)
液滴饱和温度 (K)
当壁面温度 达到临界过渡温度 ,标志着膜沉积的开始,使用方程 12.239 (第 509 页) 来定义临界温度因子 :
更具体地说,Kuhnke模型考虑了以下几种情况:
- 扩散:在以下任一条件下,将撞击的液滴加入壁面液膜中:
-
当且墙面湿润时
-
回弹:在以下任一条件下,撞击的液滴会原封不动地反弹,尺寸不变:
-
且墙面潮湿
-
飞溅效果:若满足以下条件,则将水滴雾化为更小的水滴:
在飞溅状态下,根据壁面温度和壁面表面条件,部分撞击的液滴质量可能会沉积形成液膜(溅射),或者液滴可能被完全雾化(干溅射或热破碎)。
临界转变参数 和 计算如下。
与壁面温度相关的转变由临界温度因子 控制,其值根据应用在 1.1 到 1.5 之间变化。 的默认值为 1;因此,默认的临界转变温度 将等于液滴液体的饱和温度 。Kuhnke [324](第 1076 页)建议单个液滴撞击时取 1.1,液滴链撞击时取 1.16。对于大多数尿素-水悬浮液, 设定为 1.4 [66](第 1060 页)。
作为拉格朗日壁面液膜模型的替代方案,临界转变温度 可以通过液体的饱和温度 加上一个恒定偏移量 来计算:
对于SCR悬浮液,推荐的值范围在167至之间。
参数的两个关键值(一个对应于高温下反弹与热破碎之间的转变,即,另一个对应于低温下沉积与溅射之间的转变,即)取决于多个参数和壁面条件(湿或干),具体描述如下。
- 湿壁
无量纲薄膜高度 的计算公式如下:
其中, 表示液膜高度 , 表示液滴直径 。
公式 12.242(第 510 页)中的其他参数表述如下:
这里,、、、、 和 是常数,其值如公式 12.242(第510页)所示。
- 干墙
其中
无量纲表面粗糙度
表面粗糙度 (m) (平均绝对距离与均值的比值)
以及
将下面的文本翻译成中文:与
其中, 是混合函数的阈值转换值,设定为 0.99,而 则代表混合区域的宽度。
参数 在 20 至 40 之间随机取样。
其中, 是一个在 0 到 1 之间均匀分布的随机数:
参数 是通过以下方程计算的:
将下面的文本翻译成中文:随着
式中
飞溅质量分数确定如下:
式中
12.9.3.2.2 反弹
在反弹状态下,反弹粒子的速度由以下公式给出:
其中,
其中, 和 分别表示反弹速度的切向和法向分量, 是入射速度的切向分量,而 则是通过以下公式计算得到的法向恢复系数:
其中, 是冲击前的正常冲击韦伯数。
反弹颗粒的偏差角 ,从入射方向随机取值在 -90° 到 90° 之间。
12.9.3.2.3 飞溅
图 12.11:Kuhnke 模型:冲击液滴(第 513 页)图形化地描述了 Kuhnke 飞溅模型中的以下飞溅液滴变量:
-
冲击颗粒的直径,
-
冲击颗粒的速度, 加上变异性
-
飞溅的次级颗粒的直径,
-
飞溅颗粒的平均速度, 加上变异性
-
冲击角度 ,从壁面测量
-
飞溅颗粒的反射角度 ,从壁面测量
-
从入射方向的偏差角 注意:
注意,通常情况下,冲击和反射角度在 Stanton/Rutland 和 Kuhnke 模型框架中测量方式不同:
-
Stanton 和 Rutland 模型:从壁面的法线测量
-
Kuhnke 模型:从壁面测量
图 12.11:Kuhnke 模型:冲击液滴
飞溅颗粒的属性计算如下。
首先,飞溅液滴的平均直径计算如下:
将下面的文本翻译成中文:随着
其中
主液滴直径
冲击颗粒的正常冲击韦伯数
冲击角度,单位为弧度
接下来,根据Stanton和Rutland [629](第1093页),[631](第1093页)的原始提议,飞溅液滴直径 从连续Weibull概率密度函数 的逆函数中随机采样,该函数描述如下:
当 时,也采用了如《飞溅》(第503页)中所述的极限方法。
每个飞溅包裹中的液滴数量根据总体质量平衡,通过方程12.222(第506页)确定。
平均飞溅液滴速度 是根据次级韦伯数 和平均液滴尺寸 计算得出的:
式中
其中, 和 是基于绝对颗粒速度的,并且
与溅射液滴直径类似,溅射液滴速度 从连续Weibull概率密度函数的倒数中随机抽样,其分布平均值为 。
喷射角度 则通过假设一个逻辑分布,从平均值 计算得出:
角度(以度为单位)按照逻辑PDF logistic 分布,其中 。
此处使用的符号如下:
无量纲表面粗糙度
表面粗糙度 (最大高度差的平均值)
连续逻辑PDF的逆函数由以下公式给出:
偏差角 的确定方法如下:
式中
12.9.3.3 随机Kuhnke模型
随机Kuhnke模型的状态图如图12.12所示:随机Kuhnke模型的状态图(第515页)。
图12.12:随机Kuhnke模型的状态图
该模型通过根据临界温度和韦伯数转换标准将所有相关的冲击现象分类为以下四个核心状态,考虑了所有相关的冲击现象:
-
反弹
-
扩散
-
飞溅
-
蒸发飞溅
扩散和飞溅状态导致壁膜的形成。此外,引入了过渡状态以避免在膜沉积过程中发生突变。
状态转换标准定义如下。定义了上下沉积极限和之间的临界温度范围:
其中,
液膜饱和温度 [K]
上沉积极限偏移
沉积范围温度差
韦伯数准则在湿壁和干壁上的定义有所不同:
- 湿壁上溅射的临界韦伯数:
- 干壁溅射临界韦伯数:
在公式12.266(第515页)和公式12.267(第516页)中:
拉普拉斯数
拉普拉斯数常数
根据表12.2插值得到的壁面粗糙度的函数:参数作为壁面粗糙度的函数(第516页)
表12.2:参数作为壁面粗糙度的函数
| (微米) | A |
|---|---|
| 0.05 | 5264 |
| 0.14 | 4534 |
| 0.84 | 2634 |
| 3.1 | 2056 |
| 12 | 1322 |
拉普拉斯数表示为:
其中,
液滴密度
液滴表面张力
液滴直径
液滴粘度
最后,Stochastic Kuhnke 模型根据液滴的韦伯数(参见 Ansys Fluent 理论指南中“Kuhnke 模型”部分的韦伯数定义)和壁面条件,为每次撞击事件分配适当的模式。这些模式包括:
- 反弹
冲击后的液滴在大小不变的情况下被喷射出去。根据Ansys Fluent理论指南中关于Kuhnke模型的“反弹”部分,计算了反弹颗粒的速度分量。
- 扩展:
在流体动力学模拟中,液滴的冲击与反弹行为是研究的重要环节。本段描述了液滴在受到冲击后,其尺寸保持不变,并被重新发射出去的现象。这一过程的速度分量计算,是依据Ansys Fluent软件中的Kuhnke模型进行的,该模型详细规定了液滴反弹时的物理行为,确保了模拟结果的准确性与可靠性。通过这样的模拟,科研人员能够更好地理解液滴在复杂环境中的动态响应,进而为相关工程应用提供理论支持。
撞击的液滴被加入到壁膜中。
- 飞溅
冲击液滴的一部分质量沉积形成薄膜,其余部分则被雾化。飞溅质量分数和飞溅液滴变量根据Ansys Fluent理论指南中Kuhnke模型的“飞溅”部分进行计算。
- 蒸发飞溅
区域边界: 且
假设一小部分冲击的液体喷雾在撞击时立即蒸发,而其余部分则完全雾化,释放出较小尺寸的液滴。此区域内发生的蒸发事件由随机数采样控制。与飞溅区域类似,飞溅液滴变量如Ansys Fluent理论指南中Kuhnke模型的“飞溅”部分所述进行计算。
- 过渡区域
区域边界: 且
在这些条件下,冲击液滴可能被分配到任意一个区域(扩散、飞溅或蒸发飞溅)。这取决于随机数与从公式12.269(第517页)计算出的沉积比的比较,结合液滴韦伯数和湿壁或干壁标准。
12.9.4 分离与剥离子模型
关于薄膜分离模型的详细描述,请参见薄膜分离(第840页)。有关薄膜剥离模型的详细信息,请参见薄膜剥离(第842页)。
12.9.5 壁面薄膜颗粒的守恒方程
以下描述了壁面薄膜中单个颗粒的动量、质量和能量守恒方程。基于颗粒的方法最初由O'Rourke [495](第1086页)提出,后续推导大部分基于该工作。
12.9.5.1 动量
薄膜中颗粒的动量方程为: 表示薄膜颗粒速度
表示气体流对薄膜表面剪应力的大小
表示薄膜表面速度方向的单位向量
表示壁面对薄膜施加的应力
表示保持薄膜在表面所需每单位面积的力
表示颗粒位置处的当前薄膜高度
表示体积力项
尽管薄膜厚度值很小,但由于在移动边界模拟中观察到极高的加速度率,体积力项可能变得非常重要。
壁面应力 的表达式为: 其中, 代表液膜粘度,而 则是壁面速度。
力 虽然为了完整性被包含在第12.270节(第517页)的方程中,但在Fluent求解的方程组中并未对其进行建模。取而代之的是,通过明确施加以下条件来考虑其影响: 在每个时间步长,对于所有代表壁膜的粒子,Ansys Fluent 求解一个形式如下的粒子位置方程: 在重新排列方程12.270(第517页)并代入方程12.271(第518页)后,薄膜粒子的加速度可表示为:
12.9.5.2 薄膜传质
12.9.5.2.1 薄膜蒸发与沸腾
当薄膜颗粒温度高于蒸发温度 时,应用薄膜蒸发定律。在 Ansys Fluent 中,蒸发速率采用以下模型进行建模:
-
扩散控制模型
-
对流/扩散控制模型
-
气体侧边界层模型
-
薄膜沸腾模型
12.9.5.2.1.1 扩散控制模型
薄膜蒸发速率受表面暴露于气相的梯度扩散控制。薄膜表面与气相之间的蒸汽浓度梯度决定了蒸发速率。 其中, 表示蒸气的摩尔通量 , 是传质系数 ,而 和 分别代表薄膜表面和主体气体中的蒸气浓度 。
薄膜表面的蒸气浓度通过薄膜温度下的饱和蒸气压来评估,而主体气体浓度则从流动场解中获得。蒸发的速率对饱和蒸气压非常敏感,这一点与液滴蒸发类似。
薄膜传质系数通过以下方式获得: 其中, 表示物质 的二元扩散系数, 是努塞尔特相关系数,而 len 则是特征长度(以米为单位),计算方法为薄膜包覆区域 的平方根。 被视为墙体表面积 的质量加权百分比: 在计算质量传递系数的公式12.276(第519页)中,采用努塞尔特相关性,并将普朗特数替换为施密特数,具体如下:
- 层流流动:
- 湍流: 雷诺数 是根据颗粒膜的特征长度 以及与壁面平行的颗粒相对速度分量计算得出的。
对于多组分蒸发,每个组分的扩散性用于方程 12.276(第 519 页)和方程 12.279(第 519 页)中,以获得液膜混合物中每个组分的蒸发速率。
颗粒包的质量 按照以下方式减少: 其中, 表示气相物种 的分子量,该物种是从液体中蒸发的蒸汽所加入的。为了考虑单个包裹中的质量损失,薄膜颗粒的直径会减小。这保持了包裹中液滴数量的恒定。
12.9.5.2.1.2 对流/扩散控制模型
薄膜蒸发速率由以下因素决定:
其中
物质 的蒸气质量通量
和 物质 在液膜表面和主体中的质量分数
液膜传质系数 ,根据公式 12.276计算
气体主体的密度
12.9.5.2.1.3 热解模型
单速率热解模型使用公式 12.87 (第 468 页),恒速模型使用公式 12.88 (第 468 页)。如果考虑拉格朗日壁面液膜,可以应用允许区分自由流粒子和液膜粒子热解速率的次级速率模型。该模型使用公式 12.87 (第 468 页) 分别计算从自由粒子到气体主体相的质量传递速率(使用粒子前置指数因子 和粒子活化能 )以及从液膜到气体主体相的质量传递速率(使用液膜前置指数因子 和液膜活化能 )。
12.9.5.2.1.4 气体侧边界层模型
当主体中物质的分压低于液膜表面的蒸气压时,Fluent 使用公式 12.291 (第 523 页) 和公式 12.292 (第 523 页) 分别计算层流和湍流的蒸发速率。这些公式使用壁函数来确定传质系数。详情请参见“液膜冷凝”(第 522 页)。
12.9.5.2.1.5 带有导热传热模型的液膜沸腾模型
当液膜温度达到沸点时,液膜沸腾速率通过将能量平衡方程 (公式 12.301 (第 526 页)) 的右侧设为 0 并求解液膜沸腾速率 来计算。
得到的沸腾速率表达式如下:
恒温墙体 热流墙 包含:
这里 薄膜包裹面积
潜热
薄膜包裹温度 (K)
壁面温度 (K)
主流相温度 (K)
壁面热流
薄膜高度
液态薄膜的热导率
如果启用了气体侧边界层模型,则传热系数 的计算方法如下。
-
层流流动:,其中长度 是从薄膜表面到主流的垂直距离。
-
湍流流动: 根据壁面函数确定,如《薄膜能量传递》(p. 524)中所述。
在其他情况下,Fluent 使用努塞尔数表达式: 其中
= 连续相的热导率
= 特征长度
努塞尔数 根据公式 12.299 (第 526 页) 计算。如果薄膜通过与冷壁接触而被冷却至沸点以下,蒸发速率计算将恢复到蒸发方程 (公式 12.275 (第 519 页) 或公式 12.282 (第 520 页))。
12.9.5.2.1.6 带有对流换热模型的薄膜沸腾模型
对流换热模型的沸腾速率表达式如下:
对于恒温壁: 对于热流墙: 随着 在上述方程中,
薄膜颗粒的质量(千克)
薄膜颗粒的温度(开尔文)
整体温度(开尔文)
壁面温度(开尔文)
蒸发潜热
从壁面到液膜的热传递系数
从液膜到整体相的热传递系数
液膜包裹面积,取为壁面面积的质量加权百分比
施加在壁面上的热通量(瓦特)
液体的普朗特数
从液膜到整体相的热传递系数 的获取方法如传导热传递模型中的薄膜沸腾模型所述(第520页)。
从壁面到液膜的热传递系数 的获取方法如方程12.312所述(第529页)。
如果液膜通过接触冷壁而冷却到沸点以下,蒸发速率的计算将返回到蒸发方程(方程12.275(第519页)或方程12.282(第520页))。
12.9.5.2.2 薄膜凝结
当整体中物种 的分压超过其在薄膜表面的蒸气压时,凝结模型被触发。FLUENT拉格朗日壁膜模型在层流和湍流条件下使用两种不同的表达式来描述壁膜凝结。推导遵循[739](第1100页),假设气相中物种 的凝结发生在非冷凝物的存在下。
在Ansys Fluent拉格朗日壁膜冷凝模型中,组分在存在非冷凝组分的情况下,会在壁膜上发生冷凝。对于组分通过距离膜表面处的平面的冷凝速率,菲克定律可以表述为: 物种蒸气的质量通量
主体相的密度
物种 i 的扩散系数
物种 i 的质量分数
对于层流,物种 的质量分数从薄膜表面到主体气体条件进行积分,得到对数项,而在湍流情况下,直接采用有限差分。最终表达式为:
- 层流边界层:
- 湍流边界层: 其中,
= 质量传递系数
和 = 物种 在薄膜表面和主体中的质量分数,分别
对于层流流动,方程 12.291(第 523 页)中的质量传递系数 计算如下: 其中, 是从薄膜表面到本体区域的法向距离。 计算为从相邻壁面单元中心到壁面的法向距离。
对于湍流流动,方程 12.292(第 523 页)中的湍流质量传递系数 由壁面函数确定。当前实现使用方程 4.348(第 141 页)所述的壁面函数。当在湍流模型中启用增强壁面处理时,实现遵循增强壁面处理 方程(EWT-ε)(第 145 页)中的计算。
对于多组分颗粒,方程 12.291(第 523 页)或方程 12.292(第 523 页)分别应用于每个液体组分。
有关如何使用薄膜冷凝模型的更多信息,请参阅《Fluent 用户指南》中的薄膜冷凝模型部分。
12.9.5.2.3 多组分薄膜模型
对于多组分拉格朗日壁面薄膜,蒸发速率计算为各组分蒸发速率的总和。液体薄膜中每个组分的蒸发速率从以下公式计算:
-
扩散控制模型:方程 12.275(第 519 页)和方程 12.276(第 519 页)
-
对流/扩散控制模型:方程 12.282(第 520 页)
如果在薄膜中为任何组分启用了热解模型,Ansys Fluent 应用方程 12.164(第 486 页)以获得单速率下的各组分热解速率,或方程 12.165(第 486 页)以获得恒定速率。
如果考虑拉格朗日壁面薄膜,可以使用次级速率模型。该模型使用方程 12.164(第 486 页)分别计算自由流颗粒的蒸发速率(使用颗粒预指数因子 和颗粒活化能 )和薄膜的蒸发速率(使用薄膜预指数因子 和薄膜活化能 )。
当多组分膜表面的总蒸气压超过细胞压时,Ansys Fluent采用多组分膜沸腾方程,根据壁面施加的热边界条件,使用方程12.283(第520页)或方程12.284(第521页)的平均形式。平均潜热根据方程12.170(第487页)计算,基于各液体组分的潜热和膜的总体沸腾速率,通过对方程12.283(第520页)或方程12.284(第521页)计算的传导传热模型速率进行平均,以及对方程12.287(第522页)或方程12.288(第522页)计算的对流传热模型速率进行平均,并结合方程12.171(第487页)计算的分馏蒸发量,来计算每个液体组分的总体沸腾速率。
12.9.5.3 膜中的能量传递
12.9.5.3.1 传导传热模型
为了获得膜中温度的方程,必须考虑来自气体侧和壁侧的能量通量。在没有膜蒸发/沸腾的情况下,从/到膜粒子的能量传递由以下公式给出: 其中,
, 和 分别表示薄膜包裹的质量、比热容和温度。
表示从壁面传导的热量。
表示薄膜表面处的对流热通量。
图 12.13:薄膜中双线性温度分布的假设

当壁面上的热边界条件设定为恒定温度时, 计算如下: 其中
液膜的热导率
根据方程12.278(第519页)计算的液膜包面积
液膜高度
对于热通量由边界条件给定的壁面,,方程12.295(第525页)被替换为: 对流热通量,即 ,其计算公式如下: 其中,
传热系数
薄膜表面温度
如果启用了薄膜冷凝或气体侧边界层模型,传热系数 的计算方法如下:
-
层流: 其中, 表示从薄膜表面到体相内部的法向距离。 的计算方法是从相邻壁面单元的中心到壁面的法向距离。
-
湍流流动:
的确定依赖于壁面函数。当前的实现采用了标准壁面函数(第138页)中描述的壁面函数,具体见方程4.343(第140页)。当湍流模型中启用了增强壁面处理时,实现遵循增强壁面处理 方程(EWT- )(第145页)中的计算方法。
在其他情况下,Fluent 使用努塞尔数表达式来计算 : 式中
努塞尔数 的计算公式如下:
在公式12.297(第525页)中,薄膜表面温度 ( T_s ) 是根据界面守恒关系确定的: 当粒子在蒸发过程中质量发生变化时,需在方程12.294(第524页)中增加一项,以考虑蒸发热的影响: 其中, 是液膜包裹体的蒸发速率 ,而 是蒸发潜热 (J/kg)。
在计算液膜包裹体的轨迹时,Ansys Fluent 会积分方程 12.294 (第 524 页) 或方程 12.301 (第 526 页),并得到下一个时间步长的温度。
该实现未考虑液膜辐射效应。能量源项是根据液膜轨迹上的能量差计算得出的。对于液膜附着在施加热流量的壁面上的情况,液膜与壁面之间的热损失或热增益等于热流量值。对于所有其他热边界条件(除热流量外),Fluent 根据壁面温度和从主流体传递到液膜的热量来确定液膜温度。然后,通过将主流体到壁面的热流量和液膜到壁面的热流量相加,计算出总的热流量。
12.9.5.3.2 对流换热模型
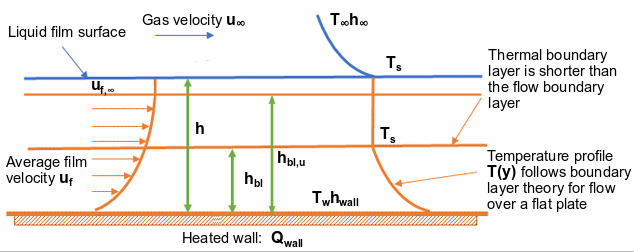
对流壁面液膜换热模型提供了更精确的计算方法,用于计算拉格朗日壁面液膜与形成它的壁面之间的热传递。这对于较厚的壁面液膜、高速移动的液膜以及液膜液体材料的普朗特数较高的情况特别有用。请参阅 Fluent 用户指南中的“设置拉格朗日壁面液膜模型”部分,了解如何使用此模型。
对于液体薄膜中的流动和传热,做出以下假设:
-
液膜流动是层流的。
-
液体薄膜中的速度和温度分布遵循层流边界层理论,适用于流过平板的情况,如 [372] (第 1078 页) 所述。
-
速度边界层 位于热边界层 之上。
-
当薄膜高度远低于热边界层时,传热过程将回归到纯导热状态。
-
薄膜始终与壁面完全接触。
图12.14:对流壁-薄膜传热:加热表面上的薄膜流动
一个温度为 的薄膜颗粒与壁面及主体相交换热量的能量平衡可以表示为: 将下面的文本翻译成中文:与 以及 其中
薄膜颗粒的质量(kg)
液体的比热容
薄膜颗粒的温度(K)
蒸发的潜热
从壁面到液体薄膜的热传递系数
从液体薄膜到主体相的热传递系数
壁面面积
薄膜包裹面积,取为壁面面积 的质量加权百分比(m²)
主体温度(K)
薄膜表面温度
壁面温度
施加在壁面上的热通量(W)
在垂直于壁面方向 的热边界层内的温度分布表示为: 其中, 表示边界层高度。
在热边界层上方的膜温度保持恒定,为 。
边界层内的平均温度 可以通过沿 方向积分得到: 从而得出: 在假设薄膜速度和密度保持恒定的前提下,可以通过对和分别以高度和进行加权,从而得到平均薄膜温度。 其中, 表示液膜高度。
对于 的情况,热边界层厚度与速度边界层厚度之比可以表示为: 表面温度 ( T_s ) 可通过结合方程 12.307(第528页)
- 以及适用于恒温壁面的方程 12.309(第528页)来计算: 对于施加了恒定热流 的墙体,其表面温度的相应方程可表示为: 在计算薄膜颗粒轨迹的过程中,Ansys Fluent 会整合方程 12.302(第 527 页),并获取下一时间步的温度。
该模型的实现并未考虑薄膜辐射效应。能量源项是根据薄膜轨迹上的能量差异,针对薄膜颗粒计算得出的。对于薄膜附着在施加热流量的壁面上的情况,薄膜与壁面之间的热损失或热增益等于热流量值。对于所有其他热边界条件(除热流量外),Ansys Fluent 会根据壁面温度以及从主流体传递到薄膜的热量来确定薄膜温度。然后,根据方程 12.304(第 527 页)计算流向壁面的总热流量。
- 计算传热系数
从薄膜到壁面的传热系数表示为: 其中, 是液膜的热导率,而 是特征长度。
努塞尔数 根据层流边界层理论计算,适用于 0.6 的情况:
- 恒温壁面:
- 恒定热流壁面: 在上述方程中,雷诺数 和普朗特数 的计算方式如下:
其中,
, 和 分别表示液膜的密度、粘度、热导率和比热容。
液膜在主体中的速度,即在液膜流动边界层之上
- 计算
在层流边界层中,完全发展流动在垂直于壁面的方向 上的速度分布描述为: 流动边界层高度 可根据距离 从平板边缘的位置获得 [372](第1078页): 大量速度 是根据平均壁膜速度 计算的,适用于以下几种情况:
-
当 时: 对于 , 是通过从 到 的外推立方速度剖面得到的。
-
关于特征长度 的考虑
是当前颗粒位置与冲击点之间的距离。冲击位置仅对新薄膜颗粒已知,并且只能在冲击事件期间记录。在读取早期版本创建的案例/数据文件中的薄膜颗粒时,无法回溯计算。对于那些旧颗粒,薄膜高度与下面的努塞尔数 表达式一起用作特征长度 ,提供了在指定长度上的平均传热系数。
对于 的努塞尔数表示为:
- 恒温壁面: 恒定热流:
- 关于传热系数的考虑
传热系数 根据公式 12.312(第 529 页)计算,与努塞尔数有关。然而,在以下条件下,它会回归到导热传热系数 :
-
雷诺数较小,这可能发生在薄膜速度较低时,或者在薄膜颗粒路径的开始阶段
-
薄膜高度远低于热边界层
在这些情况下,假设薄膜中的温度分布呈线性,且特征长度将等于薄膜高度 len 。
导热传热系数计算如下:
- 湍流薄膜近似法在传热中的应用
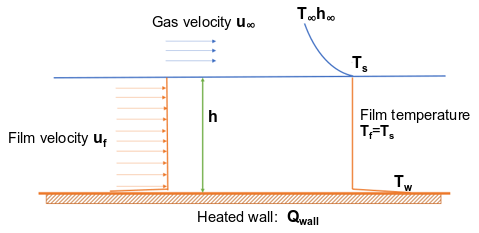
在高薄膜雷诺数情况下,由于湍流现象,薄膜与壁面间的传热显著增强。Ansys Fluent 提供了一种简化方法,当薄膜处于湍流状态时,这种方法能提高传热预测的准确性。
仅就传热计算而言,以下假设被采用:
-
过渡流态和完全湍流流态均基于薄膜局部雷诺数来定义。
-
在完全湍流流态中,薄膜内的速度和温度分布均呈平坦状(参见图12.15:完全湍流薄膜流态:速度和温度分布假设 (第531页))。
图12.15:完全湍流薄膜流态:速度和温度分布假设
雷诺数 表示为 其中, 表示液膜平均速度,其余符号与公式 12.315(第529页)中的定义相同。对于壁面与液膜间传热的努塞尔数 ,在完全湍流流动区域()下,定义如下:
通过在方程12.310(第528页)或方程12.311(第529页)中设置 ,可以实现平坦的温度分布。
- 过渡流态 :
努塞尔数定义为通过方程12.326(第532页)以及方程12.313(第529页)或方程12.321(第530页)计算得到的最大数。立方温度分布假设(方程12.305(第528页))仍然保持。 这里: 以及 对于完全湍流流动状态,数被设定为方程12.326(第532页)和方程12.324(第531页)预测值中的最小值。
数的限制已根据Åkesjö等人报告的数据进行校准[12](第1057页)和[86](第1061页):
- 冲击点处壁面到液膜传热系数的计算
在颗粒冲击点处,边界层理论不再适用。此处采用以下表达式计算努塞尔数 [373](第1078页): 此处,雷诺数可表示为:
其中, 表示射流速度 。
上述表达式中使用到的特征长度 是射流直径,该直径近似于相关喷射类型的参考直径。参考直径定义为
与表面喷射的表面积相对应的水力直径,或涉及粒径分布的喷射中的最大粒径。