本节阐述了Transition SST模型的理论基础。相关信息将在以下章节中详细介绍：

• 4.7.1. 概述
• 4.7.2. Transition SST模型的输运方程
• 4.7.3. 网格要求
• 4.7.4. 指定入口湍流水平

如需了解在Ansys Fluent中使用该模型的具体细节，请参阅用户指南中的“湍流建模”及“设置Transition SST模型”部分。

4.7.1 概述

Transition SST模型（亦称为$\gamma$ - ${\mathrm{Re}}_{\theta }$模型）基于SST $k$ – $\omega$输运方程与另外两个输运方程的耦合，一个用于间歇性参数，另一个用于以动量厚度雷诺数表示的转捩起始准则。ANSYS开发了一种经验相关性（Langtry和Menter），旨在涵盖标准旁路转捩及低主流湍流环境中的流动情况。

此外，还包含了一个非常强大的选项，允许用户输入自定义的经验相关性，进而控制转捩起始动量厚度雷诺数方程。

请注意以下限制：

• Transition SST 模型仅适用于壁面约束流动。与其他所有工程转捩模型一样，该模型不适用于自由剪切流中的转捩现象。该模型会将自由剪切流预测为完全湍流状态。
• Transition SST 模型不具备伽利略不变性，因此不应应用于相对于计算速度场的坐标系移动的表面；对于这种情况，应改用间歇性转捩模型。
• Transition SST 模型设计用于具有定义的非零自由流速度的流动（即经典的边界层情况）。它不适用于没有自由流的完全发展的管道/通道流动，同样也不适用于壁面射流流动。对于这些场景，应改用间歇性转捩模型。但请注意，可能需要通过修改底层相关性来调整这些流的间歇性转捩模型。
• Transition SST 模型的校准未结合影响湍流模型源项的其他物理效应进行过校准，例如：
  • 浮力
  • 多相湍流

要了解如何设置Transition SST模型的信息,请参阅用户指南中的"设置Transition SST Model"部分.

4.7.2 Transition SST Model 传输方程

间歇性 $\gamma$ 的输运方程定义为：

$$\frac{\partial (\rho \gamma )}{\partial t}+\frac{\partial (\rho U_j\gamma )}{\partial x_j}=P_{\gamma 1}-E_{\gamma 1}+P_{\gamma 2}-E_{\gamma 2}+\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\gamma }}\right)\frac{\partial \gamma }{\partial x_j}\right]\text{\hspace{1em}(4.169)}$$

转捩源的定义如下：

$$\begin{array}{rl}& P_{\gamma 1}=C_{a1}{F}_{length}\rho S[\gamma F_{onset}{]}^{c_{\gamma 3}}\\ & E_{\gamma 1}=C_{e1}{P}_{\gamma 1}\gamma \end{array}\text{\hspace{1em}(4.170)}$$

其中，$S$ 表示应变率大小，$F_{\text{length}}$ 是一个经验相关系数，用于控制转捩区域的长度，而 $C_{a1}$ 和 $C_{e1}$ 分别取值为2和1。破坏/再层流化源项定义如下：

$$\begin{array}{rcl}{P}_{\gamma 2}& =& C_{\alpha 2}\rho \Omega \gamma F_{turb}\\ E_{\gamma 2}& =& C_{e2}{P}_{\gamma 2}\gamma \end{array}\text{\hspace{1em}(4.171)}$$

其中，$\Omega$ 表示涡量大小。转捩起始受以下函数控制：

$$\begin{array}{rl}R{e}_V& =\frac{\rho y^{2}S}{\mu }\\ R_T& =\frac{\rho k}{\mu \omega }\end{array}\text{\hspace{1em}(4.172)}$$

$$\begin{array}{rl}& F_{onset1}=\frac{R{e}_{\nu }}{2193R{e}_{\theta c}}\\ & F_{onset2}=min\left(max\right(F_{onset1},F_{onset1}^4),2.0)\end{array}\text{\hspace{1em}(4.173)}$$

$$\begin{array}{rlrl}& F_{onset3}& & =max[1-(\frac{R_T}{25}{)}^3,0]\\ & F_{onset}& & =max(F_{onset2}-F_{onset3},0)\\ & F_{turb}& & =e^{-{\left(\frac{R_{\gamma }}{4}\right)}^4}\end{array}\text{\hspace{1em}(4.174)}$$

其中，$y$ 表示壁面距离，而 $R{e}_{\theta c}$ 是临界雷诺数，即边界层中不连续性首次开始增加的点。这一现象发生在转捩雷诺数 $\widetilde{R{e}_{\theta t}}$ 的上游，两者之间的差异需通过经验相关性来确定。$F_{length}$ 和 $R{e}_{\theta c}$ 的相关性均依赖于 $R{\tilde{e}}_{\theta t}$。

间歇方程的常数为：

$$C_{a1}=2;C_{e1}=1;C_{a2}=0.06;C_{e2}=50;c_{\gamma 3}=0.5;{\sigma }_{\gamma }=1.0\text{\hspace{1em}(4.175)}$$

转捩动量厚度雷诺数 $R{\tilde{e}}_{\theta t}$ 的输运方程为

$$\frac{\partial \left(\rho R{\tilde{e}}_{\theta t}\right)}{\partial t}+\frac{\partial \left(\rho U_{j}R{\tilde{e}}_{\theta t}\right)}{\partial x_j}=P_{\theta t}+\frac{\partial }{\partial x_j}\left[{\sigma }_{\theta t}\left(\mu +{\mu }_t\right)\frac{\partial R{\tilde{e}}_{\theta t}}{\partial x_j}\right]\text{\hspace{1em}(4.176)}$$

源项定义如下：

$$\begin{array}{rl}{P}_{\theta t}& =c_{\theta t}\frac{\rho }{t}\left(R{e}_{\theta t}-R{\tilde{e}}_{\theta t}\right)\left(1.0-F_{\theta t}\right)\\ t& =\frac{500\mu }{\rho U^2}\end{array}\text{\hspace{1em}(4.177)}$$

$$F_{\theta t}=min\left(max\left(F_{wake}{e}^{{\left(-\frac{y}{\delta }\right)}^4},1.0-{\left(\frac{\gamma -1/50}{1.0-1/50}\right)}^{{}^2}\right),1.0\right)\text{\hspace{1em}(4.178)}$$

$$\begin{array}{rl}{\theta }_{BL}& =\frac{R{\tilde{e}}_{\theta t}\mu }{\rho U}\\ {\delta }_{BL}& =\frac{15}{2}{\theta }_{BL}\\ \delta & =\frac{50\Omega y}{U}{\delta }_{BL}\end{array}\text{\hspace{1em}(4.179)}$$

$$\begin{array}{rcl}R{e}_{\omega }& =& \frac{\rho \omega y^2}{\mu }\\ & & \\ F_{wake}& =& e^{-{\left(\frac{R{e}_{\omega }}{1E+5}\right)}^2}\end{array}\text{\hspace{1em}(4.180)}$$

$R{\tilde{e}}_{\theta t}$ 方程的模型常数为：

$$c_{\theta t}=0.03;{\sigma }_{\theta t}=2.0\text{\hspace{1em}(4.181)}$$

壁面上$R{\tilde{e}}_{\theta t}$的边界条件为零通量。入口处$R{\tilde{e}}_{\theta t}$的边界条件应根据基于入口湍流强度的经验相关性计算得出。

该模型包含三个经验相关性。$R{e}_{\theta t}$是实验观察到的转捩起始点，此项已从Menter等人[433]（第1082页）的原始内容进行修改，以改善自然转捩预测效果，并应用于公式4.176（第78页）中。$F_{\text{length}}$表示转捩区的长度，代入公式4.169（第78页）中使用。$R{e}_{\theta c}$则是模型激活点，用以匹配$R{e}_{\theta t}$和$F_{length}$两个参数，并在公式4.173（第78页）中应用。这些经验相关性由Langtry和Menter提供[335]（第1076页）。

$$\begin{array}{c}R{e}_{\Theta t}=f\left(Tu,\lambda \right)\\ F_{length}=f\left(R{e}_{\theta t}\right)\\ R{e}_{\theta c}=f\left(R{e}_{\theta t}\right)\end{array}\text{\hspace{1em}(4.182)}$$

第一个经验相关性是局部湍流强度 $Tu$ 的函数：

$$Tu=\frac{100}{U}\sqrt{\frac{2}{3}k}\text{\hspace{1em}(4.183)}$$

其中，$k$ 表示湍流动能。

Thwaites 压力梯度系数 ${\lambda }_{\theta }$ 定义为

$${\lambda }_{\theta }=\left({\theta }^2/v\right)dU/ds\text{\hspace{1em}(4.184)}$$

其中，$dU/ds$ 表示沿流线方向的加速度。

4.7.2.1 分离诱导转捩修正

针对分离诱导转捩的修正如下：

$$\begin{array}{rlrl}& {\gamma }_{sep}& & =min\left[C_{s1}max\right[\left(\frac{R{e}_v}{3.235R{e}_{\theta c}}\right)-1,0]F_{reattch},2)F_{\theta t}\\ & F_{reattch}& & =e^{-{\left(\frac{R_{\gamma }}{20}\right)}^4}\\ & {\gamma }_{eff}& & =max(\gamma ,{\gamma }_{sep})\end{array}\text{\hspace{1em}(4.185)}$$

在这里，$C_{s1}$ 是一个常数，其值为2。

方程4.185（第79页）中的模型常数已从Menter等人[433]（第1082页）的原始数值进行了调整，以改善分离流动转捩的预测。主要变化是控制$R{e}_v$与$R{e}_{\theta c}$关系的常数从Blasius边界层的2.193调整为分离点处的3.235，该点的形状因子为3.5[433]（第1082页）。壁面处$\gamma$的边界条件是零法向通量，而对于入口，$\gamma$等于1.0。

4.7.2.2 转捩模型与SST输运方程的耦合

转捩模型通过修改$k$-方程（方程4.101（第65页））来与SST湍流模型相互作用，具体如下：

$$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\frac{\partial }{\partial x_j}\left({\Gamma }_k\frac{\partial k}{\partial x_j}\right)+G_k^{\ast }-Y_k^{\ast }+S_k\text{\hspace{1em}(4.186)}$$

$$G_k^{\ast }={\gamma }_{\text{eff }}{\tilde{G}}_k\text{\hspace{1em}(4.187)}$$

$$Y_k^{\text{*}}=\text{min}\left(\text{max}\left({\gamma }_{\text{eff}},0.1\right),1.0\right)Y_k\text{\hspace{1em}(4.188)}$$

其中，${\tilde{G}}_k$ 和 $Y_k$ 是SST模型中原有的生成项和破坏项。需要注意的是，$\omega$方程中的生成项并未被修改。上述模型公式的详细原理可在Menter等人[433]（第1082页）中找到。

为了准确捕捉层流和转捩边界层，网格的$y^{+}$应约为1。如果$y^{+}$过大（即大于5），则随着$y^{+}$的增加，转捩起始位置会向上游移动。建议您使用基于有界二阶迎风的离散化方法来处理平均流动、湍流及转捩方程。

4.7.2.3 转捩SST模型与粗糙壁面

当使用转捩SST模型并结合粗糙壁面时，必须在粘性模型对话框中启用粗糙度关联。此关联需要几何粗糙高度$K$作为输入参数，因为在从层流到湍流的转捩过程中，几何粗糙高度比等效砂粒粗糙高度$K_s$更为重要。关于如何根据几何粗糙高度、形状和分布确定适当的等效砂粒粗糙高度的指导，可以从Schlichting和Gersten [578]（第1090页）以及Coleman等人[117]（第1063页）的文献中获得。

粗糙度关联是对内置关联${\widetilde{\mathrm{Re}}}_{\theta t}$的一种修正，其定义如下：

$${\mathrm{Re}}_{\theta t,\text{ rough }}={\widetilde{\mathrm{Re}}}_{\theta t}\cdot f\left(K\right)\text{\hspace{1em}(4.189)}$$

新定义的${\mathrm{Re}}_{\theta t,\text{ rough }}$随后用于$F_{\text{length }}$和${\mathrm{Re}}_{\theta c}\cdot {\widetilde{\mathrm{Re}}}_{\theta t}$的相关性中，后者代表转捩动量厚度雷诺数。指定的几何粗糙度值将适用于所有壁面。若不同壁面需要不同的值，可指定用户自定义函数。值得注意的是，$\mathrm{K}$的函数在体积内（而非壁面上）使用。因此该函数必须覆盖边界层及其外延的应用区域。举例来说，假设一块平板上有粗糙带（x方向为流向，y方向为法向，z方向为展向）位于位置$1<x<1.2\left(\mathrm{m}\right)$处，且该区域的边界层厚度可能为$\delta$ =0.01m（展向范围 -0.1<z<0.1 (m))。以下伪代码将在各处粗糙度$\mathrm{K}0$（可以是零）与转捩带的粗糙度$\mathrm{K}1$之间切换。y方向的高度不必精确等于边界层厚度——它可以更大——只要它不影响附近其他壁面即可。

$$\begin{array}{c}f\text{step}=0\\ \text{ if }(\left(1<x<1.2\right)\text{ and }\left(0<y<0.02\right)\text{ and }\left(-0.1<z<0.1\right))\text{ fstep }=1\\ K=K0\cdot \left(1-\text{ fstep }\right)+K1\cdot \text{ fstep }\end{array}\text{\hspace{1em}(4.190)}$$

4.7.3 网格要求

图4.1（第81页）和图4.2（第82页）展示了在平板测试案例T3A中，增加和减少$y^{+}$的影响。当$y^{+}$值介于0.001至1之间时，对解的影响几乎可以忽略不计。一旦最大$y^{+}$超过8，转捩起始位置开始向上游移动。当最大$y^{+}$达到25时，边界层几乎完全变为湍流状态。对于低于0.001的$y^{+}$值，转捩位置似乎向下游移动，这可能是由于特定湍流频率$\omega$的表面值较大所致，该频率与第一个网格节点高度成比例关系。因此，应避免使用非常小的$y^{+}$值（低于0.001）。

图4.1：平板T3A测试案例中增加y+的效果

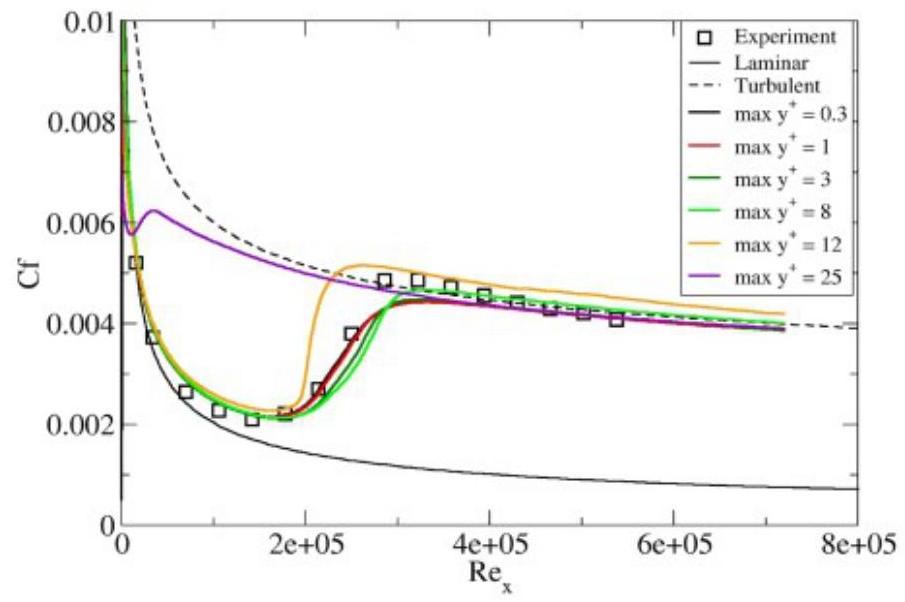
图4.2：平板上T3A测试案例中y+值降低的影响

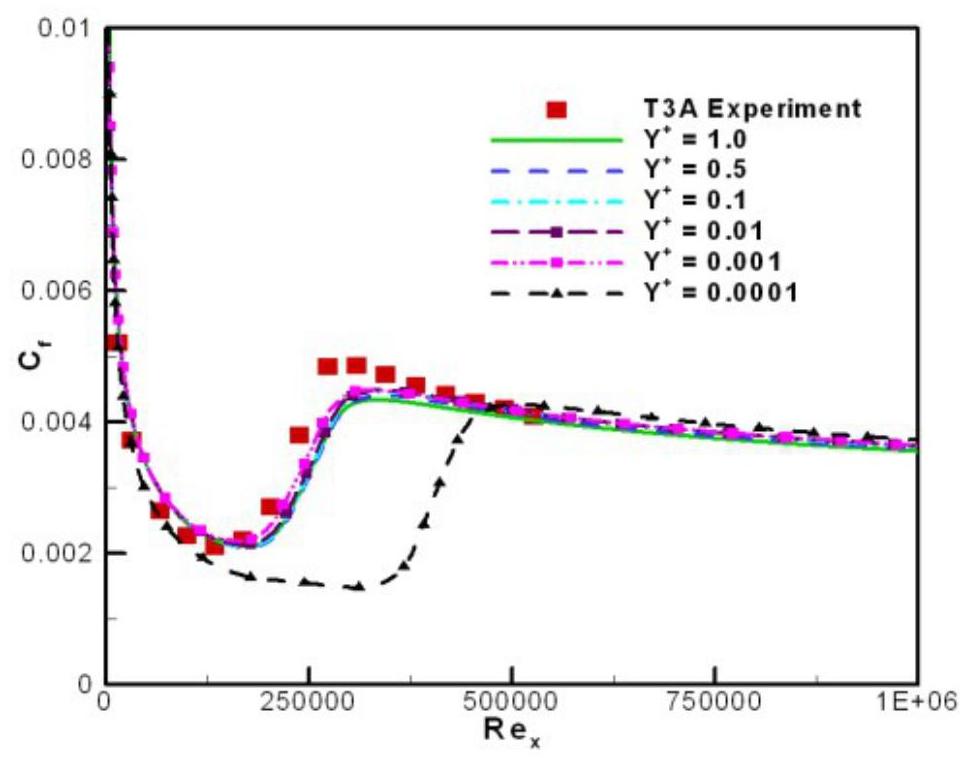
图4.3展示了从$y^{+}$值为1开始的壁面法向扩展比率的影响：平板T3A测试案例中壁面法向扩展比率的效果（第83页）。对于1.05和1.1的扩展因子，解没有受到影响。而对于更大的扩展因子如1.2和1.4，转捩位置出现了轻微但可察觉的上游偏移。由于带压力梯度的流动对壁面法向网格分辨率的敏感性可能增加，建议使用$y^{+}<1$的网格并采用小于1.1的扩展因子。

Figure 4.3: 平板T3A测试案例中壁面法向扩展比率的效果

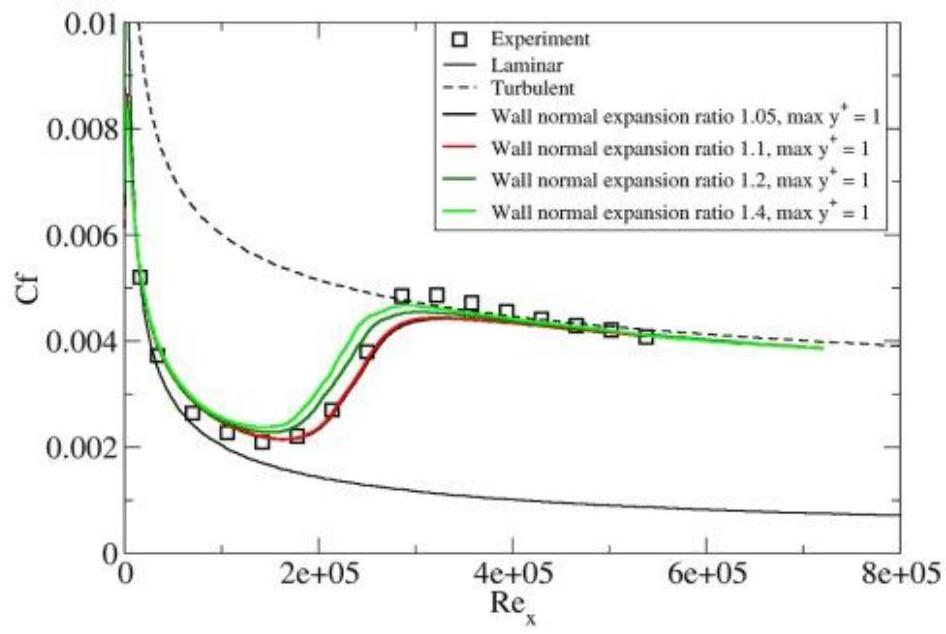
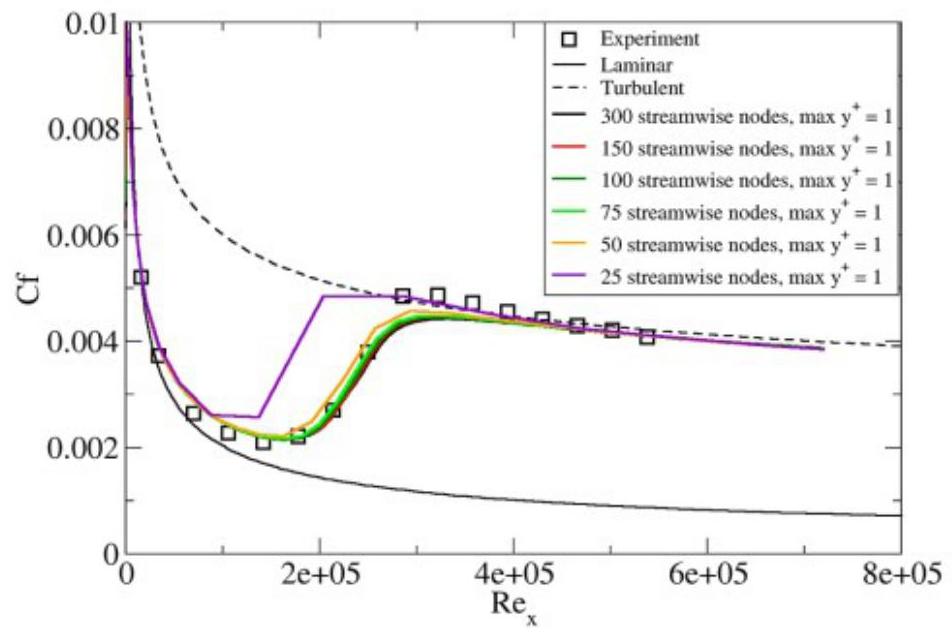
图4.4展示了沿流向网格细化的效果：平板T3A测试案例中流向网格密度的影响（第83页）。令人惊讶的是，模型对流向节点的数量并不十分敏感。只有在25个流向节点的情况下，即转捩区域仅有一个单元时，解才与网格无关解有显著差异。然而，当平板上大约有75至100个流向网格节点时，似乎出现了网格无关解。此外，分离诱导的转捩发生在极短的长度上；对于这种情况至关重要的案例来说，精细的网格是必要的。

图4.4：平板T3A测试案例中流向网格密度的影响

需要注意的是，对于锋利的导边，往往由于小型的导边分离气泡而发生转捩。如果网格过于粗糙，由分离气泡引起的快速转捩将无法被捕捉到。

根据网格敏感性研究，推荐的优化实践网格指南包括：最大$y^{+}$值为1，壁面法向膨胀比小于1.1，以及在流向方向上大约75-100个网格节点。请注意，若存在由分离引发的转捩现象时，很可能需要在流向方向上增加更多的网格节点。以涡轮叶片为例，这意味着在叶片的每一侧需要有100-150个单元格的流向分布。

4.7.4 指定入口湍流强度

观察发现，入口处指定的湍流强度会根据入口粘度比 $\left({\mu }_t/\mu \right)$（从而影响湍流涡频率）迅速衰减。因此，入口下游的局部湍流强度可能远小于入口值（参见图4.5：湍流强度（Tu）随流向距离（x）的示例性衰减 (第85页)）。通常情况下，入口粘度比越大，湍流衰减率越小。然而，如果指定的粘度比过大（即 $>100$ ），表面摩擦力可能会显著偏离层流值。有实验证据表明这种效应在物理上确实存在；但目前尚不清楚转捩模型对此行为的再现精度如何。因此，如果可能的话，最好有一个相对较低的（即 $\approx 1-10$ ）入口粘度比，并估算出合适的入口湍流强度值，以确保在叶片/翼型前缘处达到所需的湍流强度水平。可以通过以下解析解计算湍流动能的衰减： $$k=k_{\text{inlet }}{\left(1+{\omega }_{\text{inlet }}\beta t\right)}^{\frac{-{\beta }^{\ast }}{\beta }}\text{\hspace{1em}(4.191)}$$

在自由流中，SST湍流模型的常数为：

$${\beta }^{\ast }=0.09,\beta =0.0828\text{\hspace{1em}(4.192)}$$

时间尺度可以确定如下：

$$t=\frac{x}{V}\text{\hspace{1em}(4.193)}$$

其中，$x$ 表示入口下游的流向距离，而 $V$ 则是平均对流速度。涡流粘度定义如下：

$${\mu }_t=\frac{\rho k}{\omega }\text{\hspace{1em}(4.194)}$$

湍流动能衰减方程可以用入口湍流强度 $\left(T{u}_{\text{inlet }}\right)$ 和入口涡粘性比 $\left({\mu }_t/\mu \right)$ 重新表示如下：

$$Tu={\left(T{u}_{\text{inlet }}^2{\left[1+\frac{3\rho Vx\beta \left(T{u}_{\text{inlet }}^2\right)}{2\mu \left({\mu }_t/\mu \right)}\right]}^{\frac{-{\beta }^{\ast }}{\beta }}\right)}^{0.5}\text{\hspace{1em}(4.195)}$$

图4.5：湍流强度（Tu）随流向距离（x）变化的典型衰减示例

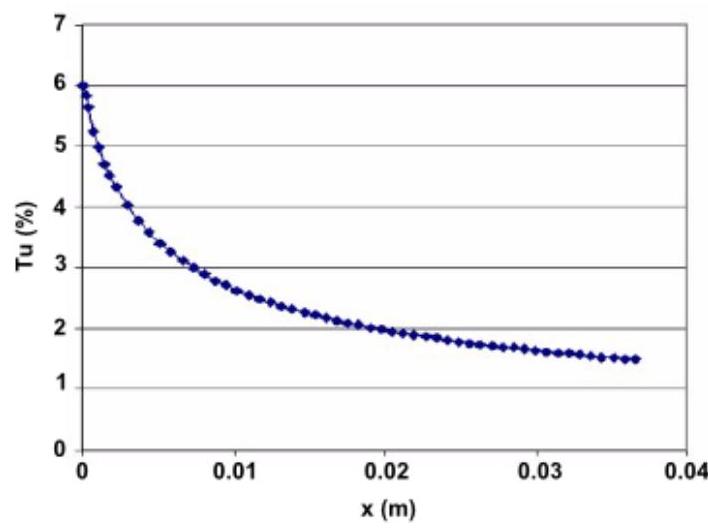
您应确保感兴趣物体周围的$Tu$值大致满足$Tu>0.1$。对于较小的$Tu$值，SST模型生成项对转捩开始的反应会变得过于迟缓，可能导致转捩延迟至物理上正确的位置之后。