引起锂离子电池（LIB）膨胀和变形的机制有多种，包括锂嵌入/脱嵌引起的电极颗粒体积变化、副反应引起的颗粒表面膜生长以及外部机械载荷引起的电极弹性变形。膨胀和变形改变了电池的电化学特性和结构机械特性（例如，几何尺寸或内应力）。Ansys Fluent使用基于物理的模型在Echem子模型水平上模拟电池膨胀效应，包括电极颗粒膨胀、夹层变形和电极孔隙率变化的基本机制。此外，结合流固耦合（FSI）结构模型，电池膨胀模型可以在CFD域的宏观水平上模拟电池单元的变形。

19.10.1 基于经验的膨胀模型

在NTGK/DCIR和ECM模型中，锂离子传输的细节并未被解析。相反，电池的电行为通过电路模型来模拟，并使用SOC（荷电状态）来追踪电池的充电状态。在经验膨胀模型中，膨胀应变 $ϵ$ 被假设为电池SOC水平的线性函数：

$ϵ = Ω (soc - so c_{re f}) / (1 + Ω^{*} so c_{re f}) (16.63)$

其中， $Ω$ 是膨胀系数，用于描述电池随着充电状态变化而膨胀的速度，soc 表示电池当前的 SOC 水平，而 $so c_{ref}$ 则是电池在无膨胀状态下的参考 SOC 水平。

您可以使用 Ansys Fluent 提供的用户自定义函数（UDF）来自定义膨胀应变公式。详情请参阅 Fluent 定制手册中的 DEFINE_BATTERY_SWELL_STRAIN。

19.10.2 基于物理的膨胀模型

基于物理的电池膨胀模型基于考虑膨胀效应的Newman’s P2D模型。 Newman P2D模型在阳极-隔膜-阴极夹层的尺度上求解锂的输运和锂的嵌入/脱离反应。通过考虑在锂嵌入/脱离反应期间电极活性颗粒的变形和在外部施加压力下夹层的弹性变形来模拟膨胀胀应。因此在电池充电期间，P2D模型的几何配置由于变形而偏离初始（或参考）几何配置，如图19.5所示

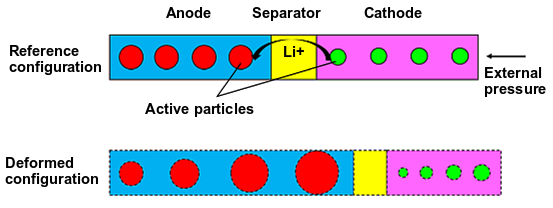
在电池膨胀模型中，在参考构型中求解P2D方程。为此应用基于连续介质力学理论的变换定律来考虑变形效应。该变换定律最初使用高阶张量来表述，假设变形在电极层中是一维的，且在粒子中是各向同性的。所有与形变相关的项都从张量退化为标量，得到的增强的P2D模型方程为：

固相中的锂守恒

$\frac{\partial C _{s}}{\partial t} = \frac{D _{s}}{r ^{2}} \frac{\partial}{\partial r} (r^{2} F_{s}^{- T} F_{s}^{- 1} \frac{\partial C _{s}}{\partial r}) (19.64)$

电解质相中的锂守恒

$\frac{\partial ( ε ^{neu} c _{e} )}{\partial t} = \frac{\partial}{\partial x} (J F^{- 1} F^{- T} D_{e}^{e ff} \frac{\partial c _{e}}{\partial x}) + \frac{a _{s}^{neu} ( 1 - t _{+}^{0} )}{F} J_{s} F_{s}^{- 1} (j^{int} + \sum j^{side}) (19.65)$

固相中的电荷守恒

$\frac{\partial}{\partial x} (J F^{- 1} F^{- T} σ^{e ff} \frac{\partial φ _{s}}{\partial x}) - a_{s}^{n e u} J_{S} F_{S}^{- 1} (j^{in t} + \sum j^{side}) = 0 (19.66)$

电解质相中的电荷守恒

$\frac{\partial}{\partial x} (J F^{- 1} F^{- T} κ^{e ff} \frac{\partial φ _{s}}{\partial x}) + \frac{\partial}{\partial x} (J F^{- 1} F^{- T} κ_{d}^{e ff} \frac{\partial ln ( c _{e} )}{\partial x}) + a_{s}^{neu} J_{s} F_{s}^{- 1} (j^{int} + \sum j^{side}) = 0 (19.67)$

式中 $F_{s}^{- 1}$ 为P2D颗粒域变形梯度逆的标量缩减； $F_{s}^{- T}$ 为P2D颗粒域变形梯度逆变的标量； $J_{s}$ 为P2D颗粒域变形梯度的行列式； $F^{- 1}$ 为P2D电极域变形梯度逆变标量； $F^{- T}$ 为P2D电极域的变形梯度逆转置减少的标量； $J$ 为P2D电极域变形梯度的行列式。其余的变量与Newman P2D模型（第838页）相同。对膨胀模型理论的更全面的描述可以在702中找到。

通过变换项，在考虑变形的情况下，在参考域（即使用原P2D网格）求解改进的P2D模型方程。上述模型方程中的固态锂浓度代表参考构型中的值。当用于计算任何电池特性时，它被转换为变形配置的值（即它的真值），例如巴特勒-沃尔默方程（方程19.18-方程19.20）中的传输电流。固相锂浓度从参考畴到形变畴的转变表示为： $c_{s} = C_{s} / J_{s} (19.68)$ 式中， $C_{s}$ 为参考域中的值； $c_{s}$ 为变形域中的值。

结果表明，颗粒锂离子嵌入和外加机械载荷都对畴变有贡献，但颗粒表面膜生长的影响没有考虑。以下变换项用于说明变形效应： $Ω_{s} = ω (\frac{C ˉ _{s}}{C _{S, m a x}} - \frac{C _{s}^{n еи}}{C _{S, m a x}}) (19.69)$

$J_{s} = 1 + Ω_{S} (19.70)$

$F_{s}^{- 1} = F_{s}^{- T} = J_{s}^{- 1/3} (19.71)$

$J = 1 + ε_{s}^{neu} Ω_{s} + \frac{σ _{nn}}{E} (19.72)$

$F^{- 1} = F^{- T} = J^{- 1} (19.73)$

方程19.65中量化了颗粒域体积变化的系数 $\overset{ˉ}{Ω}_{s}$ ，其根据电极活性材料的锂化状态（即通过锂的理论最大浓度 $C_{s, ma x}$ 归一化的颗粒域 $\overset{ˉ}{C}_{s}$ 上的平均锂浓度）而线性变化。这里， $ω$ 是描述在锂嵌入期间颗粒膨胀快慢的膨胀系数，并且 $C_{s}^{n e u}$ 为膨胀-中性状态下的锂浓度，其用作标记膨胀-中性状态的线性公式中的偏移，即其中颗粒体积没有变化。 $ω$ 和 $C_{s}^{n e u}$ 均为使用者指定的模型参数。

方程19.68中， $ε_{s}^{n e u}$ 为膨胀中性状态下的活性材料孔隙率； $σ_{nn}$ 为垂直于电池电极夹层施加的机械压力， $E$ 是杨氏模量。方程19.68中的第二项和第三项分别是由颗粒膨胀引起的电极变形和电极弹性变形。 $ε_{s}^{n e u}$ 和 $E$ 是使用者指定的参数。

除了变形之外，模型公式还包括电极孔隙率的变化。在公式19.60中-公式19.63，除了一些参考属性（上标 $n e u$ ），所有其他孔隙度相关性质（如方程19.21和方程19.22中的有效电导率 $k^{e ff}$ 和扩散率 $D_{e}^{e ff}$ ）具有以下包括溶胀效应的改进的孔隙率：

电解质孔隙率：

$ε_{e} = \frac{1}{J} ε_{e}^{n e u} (19.74)$

活性材料孔隙率：

$ε_{S} = \frac{J _{S}}{J} ε_{s}^{n e u} (19.75)$

与公式19.65中的膨胀-中性状态锂浓度一样，公式19.70和公式19.71中的膨胀-中性状态孔隙率也是用户指定的模型参数。

注：填充材料的孔隙率隐含地受到膨胀效应的影响，因为所有不同材料组分的孔隙率之和应该等于1。

19.10.3 膨胀与FSI结构模型的耦合

当MSMD电池模型与流固耦合结构模型耦合时，电极层的变形和电化学过程用基于物理的电池膨胀模型求解，宏观尺度的电池单元变形则用基于流固耦合结构模型求解。

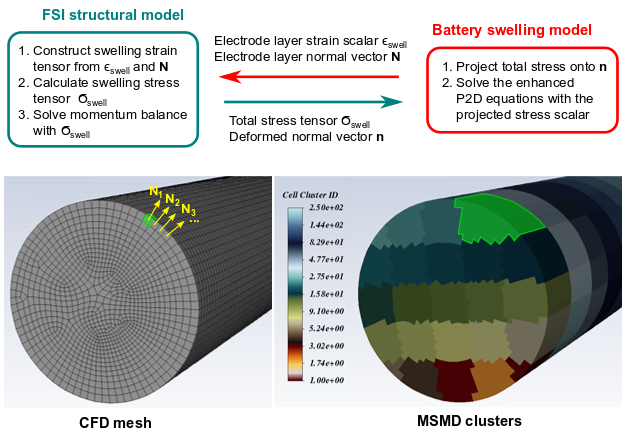
在模拟过程中，电池膨胀模型计算了嵌入CFD控制体内的电池夹层膨胀引起的有效应变，并将其传递给结构模型。反过来，结构模型计算施加在电池夹层上的有效外压力，并将其传递给电池膨胀模型。此外，由于电池膨胀模型是一维的，而FSI结构模型是三维的，因此在两个模型之间值传递一个方向的信息（即电极层的法向方向），以在标量和张量之间来回转换耦合变量。

图19.6说明了耦合变量的的两种不同空间分辨率水平。 FSI结构模型在CFD网格上求解，而Echem子模型在MSMD单元簇上迭代求解，MSMD单元簇是组合在一起以节省计算成本的CFD控制体集合。单个CFD控制体及其相应的MSMD单元簇以绿色并排显示。当耦合变量从电池传递到结构求解器时，膨胀应变标量的单个簇值被分配给簇内的所有CFD控制体。当耦合变量从结构传递到电池求解器时，投影应力标量在簇内所有CFD控制体积中被体积平均。

当求解E-Chem子模型时，机械压力的机械载荷输入（在方程19.68中使用）被计算为投影到局部电极层表面上的总应力张量的法向分量： $σ_{nn} = n^{T} σ_{t} n (19.76)$ 式中， $σ_{t}$ 为由FSI结构模型得到的总应力张量； $n$ 为电池电极层在变形坐标系中的法向量 $N$ ，该法向量是基于用户指定的参考框架的法向量计算的，并且包括几何变形的影响。

电极层的应变标量 $ε_{s w e ll}$ 计算为膨胀引起的变形在P2D电极域上的平均值： $ϵ_{s w e ll} = \frac{1}{l _{n} + l _{s} + l _{p}} \int_{x = 0}^{x = l_{n} + l_{s} + l_{p}} ε_{s}^{n e u} \overset{ˉ}{Ω}_{s} d x (19.77)$ 其中， $l_{n} 、 l_{p}$ 和 $l_{s}$ 分别为负极、正极和隔板的膨胀中性厚度。其余项与方程式19.68相同。

然后用方程19.60通过方程19.63求解改进的P2D模型。

然后将应变标量和参考框架法向量传递给FSI结构模型。 FSI结构模型求解电池几何变形，并将产生的总应力和变形的框架法向量传递回Echem子模型。

注：FSI结构模型的解满足包含膨胀应力的固体力学动量平衡，并受固体材料属性（如应变-应力关系和边界约束）的影响。

19.10.4 E-Chem独立模式下的膨胀模型

与默认的Newman P2D模型类似，基于物理的电池膨胀模型也可以在E-Chem独立模式下求解。在这种情况下，可以在Fluent中为电池夹层模拟模以下类型的机械载荷：

垂直于电极层施加的外部压力 $P_{e x t}$ 。有效机械压力 $σ_{nn}$ 由下式获得：

$σ_{nn} = - P_{e x t} (19.78)$

电极层的总厚度变化 $Δ L_{t o t}$

有效机械压力 $σ_{nn}$ 通过下面的等式反向计算，以满足目标总厚度变化： $\frac{1}{l _{n} + l _{s} + l _{p}} \int_{x = 0}^{x = l_{n} + l_{s} + l_{p}} (ε_{s}^{neu} \overset{ˉ}{Ω}_{s} + \frac{σ _{nn}}{E}) d x = \frac{Δ L _{t o t}}{l _{n} + l _{s} + l _{p}} (19.79)$

电极层安装的有效刚度 $E_{e x t}$ （例如，电池盒）

有效机械压力通过以下公式反算，以满足外部刚度下的应力-应变关系： $\frac{1}{l _{n} + l _{s} + l _{p}} \int_{x = 0}^{x = l_{n} + l_{s} + l_{p}} (ε_{s}^{n e u} \overset{ˉ}{Ω}_{s} + \frac{σ _{nn}}{E}) d x = - \frac{σ _{nn}}{E _{e x t}} (19.80)$ 左侧表示在夹层上平均的总电极变形应变，右侧表示有效负载应变。