[toc]

本节介绍与动量方程和连续性方程的离散以及利用压力基求解器进行求解相关的特殊做法。主要内容包括：

动量方程离散
连续方程离散
压力-速度耦合
稳态迭代算法
时间推进算法
动量方程校正形式离散

考虑积分形式的稳态连续方程和动量方程，可以容易地描述这些特殊做法： $\oint ρ v \cdot d A = 0 (1)$

$\oint ρ V V \cdot d A = - \oint p I \cdot d A + \oint \overline{\overset{τ}{ˉ}} \cdot d A + \int_{V} F d V (2)$

式中， $I$ 为单位矩阵； $\overline{\overset{τ}{ˉ}}$ 为应力张量； $F$ 为力向量。

24.4.1 动量方程离散

标量输运方程的离散方法也可用于动量方程的离散。例如动量方程可以通过设置 $φ = u$ 来得到： $a_{P} u = nb \sum a_{nb} u_{nb} + \sum p_{f} A \cdot \hat{I} + S (3)$ 如果压力场和网格面质量通量已知，则可以通过离散方程直接得到速度场。然而，压力场和面质量通量通常不是先验已知的，其为求解结果的一部分。关于压力值的存储和压力梯度项的离散，有一些重要的问题需要讨论。

Fluent使用同位网格方案，即压力和速度都存储在网格中心。然而上式需要网格 $c 0$ 和 $c 1$ 之间面上的压力值，因此需要一种插值方案来根据网格中心的值来计算网格面上的压力值。

24.4.1.1 压力插值格式

Fluent提供了以下选项来对界面上的压力进行插值。一般情况下使用Second Order格式，但在Mixture或VOF多相流模拟的情况下默认使用PRESTO格式。

Linear格式：将面压力计算为相邻网格中的压力值的平均值。
Standard格式：使用动量方程系数对网格面上的压力值进行内插

$P_{f} = \frac{\frac{P _{c_{0}}}{a _{p, c_{0}}} + \frac{P _{c_{1}}}{a _{p, c_{1}}}}{\frac{1}{a _{p, c_{0}}} + \frac{1}{a _{p, c_{1}}}} (4)$

只要网格中心之间的压力变化是平滑的，这个过程就能很好地工作。当控制体之间的动量源项存在阶跃或大梯度时，压力分布在网格面处具有较高的梯度，此时不能使用该格式进行插值。如果使用这种格式，这种差异表现为网格速度的过冲/欠冲。

Standard压力插值格式难以处理包含有大体积力的流动问题，例如强旋流、高瑞利数自然对流等。在这类问题中，有必要在高梯度区域加密计算网格，以充分求解压力的变化。

另一个完成来源是Fluent假设壁面处的法向压力梯度为零。这对边界层来讲是有效的，但在存在体积力或曲率流动时是无效的。同样，无法正确解释壁面压力梯度表现为指向壁面内外的速度矢量。

Second Order格式。使用中心差分格式重构网格面压力。各网格面上的压力值由下式给出：

$P_{f} = \frac{1}{2} (P_{c_{0}} + P_{c_{1}}) + \frac{1}{2} (\nabla P_{c_{0}} \cdot r_{c_{0}} + \nabla P_{c_{1}} \cdot r_{c_{1}}) (5)$

与Standard格式和Linear格式相比，此格式可以提高计算精度。

Second Order格式不适用于使用欧拉多相流模型模拟的流动，因为流动特性可能会在网格面上发生较大变化。然而，通过将压力梯度对网格面压力的影响纳入上式，并将其与Standard格式相结合，可获得欧拉多相流的二阶格式，如下所示： $P_{f} = \frac{\frac{( P _{c_{0}} + \nabla P _{c_{0}} r _{c_{0}} )}{a p _{c, 0}} + \frac{P _{c_{1}} + \nabla P _{c_{1}} r _{c_{1}}}{a p _{c, 1}}}{( \frac{1}{a p _{c, 0}} + \frac{1}{a p _{c, 1}} )} (6)$ 对于网格正交性较差的网格使用欧拉多相流时，此格式要比PRESTO!格式更健壮。

Body Force Weighted格式。此格式通过假设压力和体积力之差值的法向梯度为常数来计算面压力。如果在动量方程（例如，浮力和轴对称旋转计算）中体积力已知时，则该方法能够获得非常好的效果。对于体积力占优的Eulerian Multi-Fluid VOF问题以及网格正交性较差的网格问题，Body Force Weighted格式比PRESTO！更稳健

当问题中包含有多孔介质时，body-force-weighted格式仅对非多孔面有效，其中，该格式考虑了显式体积力的不连续性（如重力、离心力、科里奥利力等）和密度快速变化的流动（如自然对流、VOF等）的压力梯度的不连续性。所有内部和外部多孔面都采用特殊格式处理，即使阻力不连续，该格式仍能保持网格面法向速度的连续性。

Modified Body Force Weighted 格式。此格式是Body Force Weighted格式的扩展变体，它克服了Body Force Weighted格式对高粘性和旋转流的缺点，总体上提供了更好的求解稳定性和鲁棒性。该格式仅适用于VOF和Mixture多相流模型。
PRESTO!格式。PRESTO!(PREssure STaggering Option)格式使用网格面周围的“交错”控制体的离散连续性平衡来计算“交错”面压力。这个过程在本质上类似于结构网格使用的交错网格方法[484]。注意，对于三角形、四面体、混合网格以及多面体网格，使用类似的算法可以获得类似的精度。PRESTO!格式可用于所有类型的网格。

24.4.2 连续方程离散

方程(1)在控制体上积分，可以得到下面的离散方程： $f \sum N_{f a ce} J_{f} A_{f} = 0 (7)$ 式中， $J_{f}$ 为通过网格面 $f$ 的质量通量， $J_{f} = ρ v_{n}$ 。

为了进一步处理，有必要将网格面上的速度值与相邻两个网格中心的速度 $v_{n}$ 联系起来。网格中心的速度到网格面的线性插值可能导致非物理棋盘压力。Fluent中使用高阶插值格式来计算网格面通量 $\hat{J}_{f}$ ，并按照Rhie和Chow方法对压力梯度进行校正，以防产生棋盘压力。Fluent中有两种插值方法可用于计算网格面上的速度值：基于距离的线性插值(distance-based linear interpolation)和基于动量平均（momentum-based averaging）的插值方法。

通过插值计算，面通量 $J_{f}$ 可写为： $J_{f} = \hat{J}_{f} + d_{f} (P_{c_{0}} - P_{c_{1}}) (8)$ 其中， $d_{f} (P_{c_{0}} - P_{c_{1}}) = d_{f} ((p_{c_{0}} + (\nabla p)_{c_{0}} \cdot r_{0}) - (p_{c_{1}} + (\nabla p)_{c_{1}} \cdot r_{1})) (9)$ 式中， $\hat{J}_{f}$ 取决于所使用的方法：

在distance-base方法中

$\hat{J}_{f} = \frac{ρ _{f}}{2} (v_{c_{0}} + v_{c_{1}}) \cdot \overset{n}{^} + J_{h o, d}$

在momentum-based方法中

$\hat{J}_{f} = ρ_{f} (\frac{a _{p, c_{0}} v _{c_{0}} + a _{p, c_{1}} v _{c_{1}}}{a _{p, c_{0}} + a _{p, c_{1}}}) \cdot \overset{n}{^} + J_{h o, a_{p}}$

式中项 $d_{f}$ 是 $\overset{a}{ˉ}_{P}$ 的函数， $\overset{a}{ˉ}_{P}$ 为面两侧网格的动量方程系数 $a_{P}$ 的平均值。 $p_{c_{0}}$ 、 $p_{c_{1}}$ 、 $v_{c_{0}}$ 和 $v_{c_{1}}$ 分别是网格面两侧网格内的压力和速度。 $J_{h o, d}$ 是基于单元中心和面中心之间的距离对非均匀和/或非正交网格的高阶校正。类似地， $J_{h o, a_{p}}$ 为基于与面相邻的网格的动量系数对非均匀和/或非正交网格的高阶修正。

24.4.2.1 密度插值格式

在不可压缩的流动中，Fluent对密度使用算术平均。对于可压缩流东计算(即介质密度使用ideal gas的计算)，Fluent在网格面上对密度采用迎风插值。有几种插值格式可用于网格面上的密度迎风：一阶迎风、二阶迎风（默认）、QUICK、MUSCL，中心差分和有界中心差分。

一阶迎风格式(first-order upwind)将网格面上的密度值设置为上游网格中心的密度值。该格式为压力修正方程的离散提供了稳定性，并对大多数类型的流动能够给出良好的结果。虽然这种格式为可压缩流动计算提供了最好的稳定性，但对于激波模拟有比较大的数值扩散。

二阶迎风格式(second-order upwind)比一阶迎风格式在超声速流动方面具有更好的稳定性，能够更好地捕捉激波。密度的QUICK格式与其他变量的QUICK格式类似。

重要提示：在多相流的问题中，选定的密度格式应用于可压缩相，不可压缩相使用算术平均。如果可压缩流动求解不稳定，建议先使用一阶格式获得解，然后切换到更高阶格式继续计算。

24.4.3 压力速度耦合

压力基求解器允许以分离或耦合的方式求解流动问题。Fluent提供了五种压力-速度耦合算法：SIMPLE、SIMPLEC、PISO、Coupled以及Fractional Step（对于使用非迭代时间推进方案（NITA）的瞬态计算问题）。除Coupled算法外，其他所有算法均基于预测-校正方法。

注意，SIMPLE、SIMPLEC、PISO和Fractional Step使用压力基分离算法，而Coupled使用压力基耦合算法求解。当使用欧拉多相模型时，适用的压力-速度耦合算法包括Phase Coupled SIMPLE、Multiphase Coupled及Full Multiphase Coupled。

24.4.3.1 SIMPLE算法

SIMPLE算法使用速度和压力修正之间的关系来强制质量守恒并获得压力场。

如果使用猜测的压力场 $p^{*}$ 来求解动量方程，则根据方程(8)可得到面通量 $J_{f}^{*}$ ： $J_{f}^{*} = \hat{J}_{f}^{*} + d_{f} (p_{c 0}^{*} - p_{c 1}^{*}) (10)$ 不满足连续方程，因此，在面通量 $J_{f}^{*}$ 的基础上增加一个修正值 $J_{f}^{'}$ ，修正后的面通量 $J_{f}$ ： $J_{f} = J_{f}^{*} + J_{f}^{'} (11)$ 满足连续方程。

SIMPLE算法假定 $J_{f}^{'}$ 可写为： $J_{f}^{'} = d_{f} (p_{c 0}^{'} - p_{c 1}^{'}) (12)$ 式中， $p^{'}$ 为压力修正。

SIMPLE算法将通量校正方程代入离散的连续性方程（方程7），得到网格中压力校正的离散方程： $a_{P} p^{'} = nb \sum a_{nb} p_{nb}^{'} + b (13)$ 式中， $b$ 为进入网格内的净流量。 $b = f \sum N_{faces} J_{f}^{*} A_{f} (14)$ 压力校正方程可以使用代数多网格（AMG）方法进行求解。得到求解后，可以使用下面的方法校正网格压力与面通量： $p = p^{*} + α_{p} p^{'} (15)$

$J_{f} = J_{f}^{*} + d_{f} (p_{c 0}^{'} - p_{c 1}^{'}) (16)$

式中， $α_{p}$ 为压力亚松弛因子；在每次迭代中，校正后的面通量 $J_{f}$ 完全满足离散连续性方程。

24.4.3.2 SIMPLEC

文献中提供了许多SIMPLE算法的变种。除了SIMPLE算法外，Fluent还提供了SIMPLEC算法。虽然SIMPLE算法是默认选项，但在很多的计算过程中使用SIMPLEC会有更好的效果。

SIMPLEC算法与SIMPLE算法类似，位移的区别在于面通量修正 $J_{f}^{'}$ 。在SIMPLE算法中，修正方程可表示为： $J_{f} = J_{f}^{*} + d_{f} (p_{c 0}^{'} - p_{c 1}^{'}) (17)$ 在SIMPLEC算法中， $d_{f}$ 被重定义为 $(\overline{a_{P} - \sum_{nb} a_{nb}})$ 的函数。在压力-速度耦合是求解的主要障碍的问题中，使用此修正方程可以加速收敛。

对于具有一定偏斜度的网格，网格面上的质量通量修正与相邻单元上的压力修正的差值之间的近似关系非常粗略。由于沿网格面的压力校正梯度的分量事先是未知的，因此需要类似于下面描述的PISO近邻校正的迭代过程。在初解压力修正方程后，重新计算压力修正梯度，并用于更新质量通量修正。这一过程被称为偏斜度校正，其大大降低了与高度扭曲的网格相关的收敛困难。SIMPLEC偏斜度校正使Fluent能够在高度歪斜的网格上获得求解，其迭代次数与正交性更好的网格所需的迭代次数大致相同。

24.4.3.3 PISO

压力-隐式分裂算子（Pressure-Implicit with Splitting of Operators）压力-速度耦合算法是SIMPLE算法家族的一部分，其基于压力和速度修正之间较高的近似关系。SIMPLE和SIMPLEC算法的局限性之一是在求解压力修正方程后，新的速度和相应的通量不满足动量平衡。因此必须重复计算，直到达到平衡为止。为了提高计算效率，PISO算法执行两个额外的校正：邻域校正和歪斜校正。

1、邻域校正（Neighbor Correction）

PISO算法的主要思想是将SIMPLE和SIMPLEC所需的重复计算转移到压力修正方程的求解阶段。在一个或多个附加PISO循环之后，校正后的速度更接近于满足连续和动量方程。这个迭代过程被称为动量修正或“邻域修正”。PISO算法在每次解算器迭代中需要更多的CPU时间，但它可以显著减少收敛所需的迭代次数，尤其是对于瞬态问题。

2、歪斜校正（Skewness Correction）

对于具有一定歪斜度的网格，网格面上的质量通量修正与相邻网格上的压力修正的差值之间的近似关系非常粗略。由于沿网格面上的压力校正梯度的分量事先是未知的，因此需要类似于上述PISO邻域校正的迭代过程。在初解压力修正方程后，重新计算压力修正梯度，并用于更新质量通量修正。这一过程被称为歪斜校正，其大大降低了与高度扭曲的网格相关的收敛困难。PISO歪斜校正使Fluent能够在高度倾斜的网格上获得解，迭代次数与正交性更好的网格所需的迭代次数大致相当。

3、歪斜-邻域耦合（Skewness-Neighbor Coupling）

对于具有高度偏斜度的网格，如果在同一压力修正方程源处同时耦合邻域修正和歪斜校正，则可能导致发散或缺乏稳健性。用于处理PISO算法内的邻域和歪斜校正的另一种尽管更昂贵的方法是对近邻校正的每个单独迭代应用歪斜校正的一个或多个迭代。对于经典PISO算法的每一次迭代，该技术允许根据法向压力校正梯度更精确地调整网格面质量流量校正。

24.4.3.4 Fractional-Step Method (FSM)

在FSM中，动量方程通过一种称为算子分裂或近似因式分解的数学方法从连续性方程中解耦出来。得到的解算法类似于前面描述的分离解算法。在近似因式分解中使用的形式允许控制分裂误差的阶次。因此，在非迭代时间推进(NITA)算法中， Fluent采用FSM作为速度耦合算法。

24.4.3.5 Coupled

如前所述，压力基求解器允许以分离或耦合的方式求解流动问题。与非耦合或分离方法相比，使用耦合（Coupled）方法具有一些优势。与分离求解算法相比，耦合算法获得了稳态流动的鲁棒高效单相实现，具有优越的性能。这种压力基耦合算法提供了一种替代密度基和压力基分离算法的SIMPLE型压力-速度耦合。对于瞬态流动，当网格质量较差或使用的时间步长较大时，有必要使用耦合算法。

压力基分离算法分别求解动量方程与压力修正方程，这种半隐式算法收敛速度慢。

Coupled算法同时求解基于动量和压力的连续性方程。全隐式耦合是通过对动量方程中的压力梯度项进行隐式离散，以及对面质量通量（包括Rhie-Chow压力耗散项）进行隐式离散来实现的。

在动量方程（方程3）中，压力梯度的 $k$ 分量具有下面的形式： $f \sum p_{f} A_{k} = - j \sum a^{u_{k} p} p_{j} (18)$ 式中， $a^{u_{k} p}$ 为由高斯散度定理导出的系数及压力插值格式的系数。最后，对于任何第 $i$ 个网格，动量方程分离的离散形式定义为： $j \sum a_{ij}^{u_{k} u_{k}} u_{kj} + j \sum a_{ij}^{u_{k} p} p_{j} = b_{i}^{u_{k}} (19)$ 在连续方程中，使用方程式(8)中的通量表达式替换通量平衡，从而得到离散形式： $k \sum j \sum a_{ij}^{p u_{k}} u_{kj} + j \sum a_{ij} pp p_{j} = b_{i}^{p} (20)$ 因此，将整个方程组转换为-形式后，如下所示： $j \sum [A]_{ij} X_{j} = B_{i} (21)$ 其中网格 $i$ 对网格 $j$ 的影响具有如下形式： $A_{ij} = a_{ij}^{pp} a_{ij}^{u p} a_{ij}^{v p} a_{ij}^{wp} am p; a_{ij}^{p u} am p; a_{ij}^{uu} am p; a_{ij}^{vu} am p; a_{ij}^{w u} am p; a_{ij}^{p v} am p; a_{ij}^{uv} am p; a_{ij}^{vv} am p; a_{ij}^{w v} am p; a_{ij}^{pw} am p; a_{ij}^{u w} am p; a_{ij}^{v w} am p; a_{ij}^{ww} (22)$ 未知向量和残差向量具有如下形式： $B_{i} = - r_{i}^{p} - r_{i}^{u} - r_{i}^{v} - r_{i}^{w} (23)$

$X_{j} = p_{i}^{'} u_{i}^{'} v_{i}^{'} w_{i}^{'} (24)$

式(21)采用耦合AMG进行求解。

注意压力基耦合算法不能用于非迭代时间推进（NITA）求解器中。

24.4.4 稳态迭代算法

如果进行的稳态计算，则压力基求解器的控制方程中不包含与时间相关的项。对于稳态流动，离散化描述了基于控制体积的稳态输运方程的离散。

24.4.4.1 变量的欠松弛

变量的欠松弛在所有情况下都用于某些材料特性，在求解变量的NITA求解器及在压力基耦合算法中，显式欠松弛用于动量和压力。

由于ANSYS FLUENT所求解的方程组具有非线性，因此必须控制 $φ$ 的变化。这通常是通过变量的欠松弛（也称为显式松弛）来实现的，它减少了每次迭代过程中产生的 $φ$ 变化。在一个简单的形式中，网格中变量 $φ$ 的新值取决于旧值 $φ_{o l d}$ 、计算的 $φ$ 变化量 $Δ φ$ 及欠松弛系数 $α$ ，如下所示： $$ \varphi = \varphi_{old} + \alpha \Delta\varphi \tag{24.65}\label{24.65} $$

24.4.4.2 方程欠松弛

在基于压力的求解器中，通过在离散化的方程组中引入选择性的非线性方程组，利用方程的欠松弛，也称为隐式松弛，来稳定外部非线性迭代的收敛性。这相当于特定于位置的时间步长。

$$ {\frac{a_{p} \varphi}{\alpha}=\sum_{n b} a_{n b} \varphi_{n b}+b+\frac{1-\alpha}{\alpha} a_{p} \varphi_{o l d}}\tag{24.66}\label{24.66} $$ CFL数是基于压力的耦合算法中的求解参数，可以用 $α$ 来写: $$ {\frac{1-\alpha}{\alpha}=\frac{1}{C F L}}\tag{24.67}\label{24.67} $$

24.4.5 时间推进算法

对于瞬态流动，一般输运方程的离散形式可表示为下面的形式：

$$ {\int_{V} \frac{\partial \rho \varphi}{\partial t} d V+\oint \rho \varphi \vec{V} \cdot d \vec{A}=\oint \Gamma_{\varphi} \nabla \varphi \cdot d \vec{A}+\int_{V} S_{\varphi} d V}\tag{1}\label{1} $$ 其中：

$\frac{\partial ρφ}{\partial t}$ 为输运变量 $φ$ 的瞬态导数守恒形式； $ρ$ 为密度； $v$ 为速度向量； $A$ 为网格面向量； $Γ_{φ}$ 为扩散系数； $\nabla φ$ 为 $φ$ 的梯度； $S_{φ}$ 为单位体积的源项。

Fluent中的压力基求解器默认使用隐式离散方法，所有对流项、扩散项及源项均从 $n + 1$ 时间层上的物理场进行计算。 $$ {\int_{V} \frac{\partial \rho \varphi}{\partial t} d V+\oint \rho^{n+1} \varphi^{n+1} \vec{V}^{n+1} \cdot d \vec{A}=\oint \Gamma_{\varphi}{ }^{n+1} \nabla \varphi^{n+1} \cdot d \vec{A}+\int_{V} S_{\varphi}{ }^{n+1} d V}\tag{2}\label{2} $$ 在基于压力的求解器中，总的时间离散误差由时间离散格式的选择（如一阶格式、二阶格式等）及将解推进到下一个时间步长的方式（时间推进格式）决定。时态离散介绍

一阶及二阶时间离散引入的截断误差分别为 $O (Δ t)$ 及 $O (Δ t^{2})$ 。

逐个求解方程组的分离求解过程引入了分裂误差。 Fluent中有两种时间推进方式，选择何种方式取决于希望如何控制分裂误差。

24.4.5.1 迭代时间推进方式

在迭代方式中，所有方程在给定的时间步长内迭代求解，直到满足收敛准则。因此，将解推进一个时间步通常需要许多外部迭代，如图所示。该迭代方式充分考虑了各方程的非线性及方程间的耦合，消除了分裂误差。迭代方式是ANSYS FLUENT的默认选择。

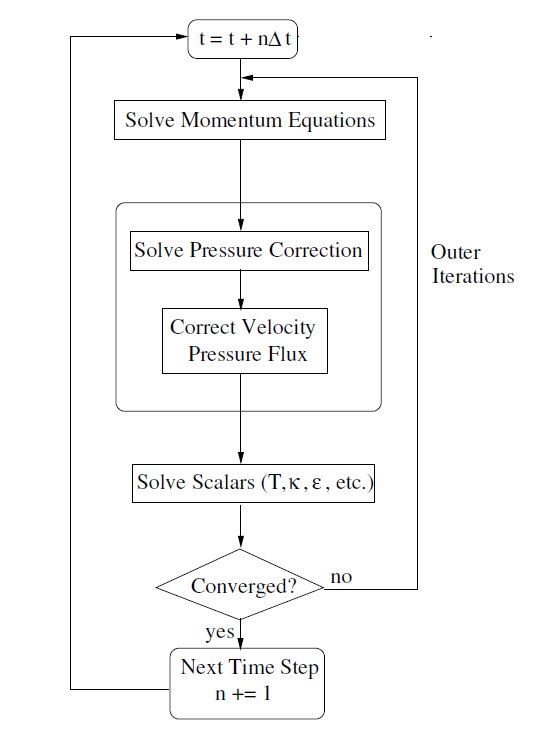
方程$\eqref{2}$中的对流部分采用标准全隐式离散会产生非线性项。此外，求解这些方程通常需要每个时间步进行大量迭代。作为替代方案，Fluent中的Frozen Flux Formulation选项提供了一种可选的方式来使用来自先前时间水平的单元面的质量通量离散对流部分。 $$ {\oint \rho \varphi \vec{v} \cdot d \vec{A}=\oint \rho^{n} \varphi^{n+1} \vec{v}^{n} \cdot d \vec{A}}\tag{3}\label{3} $$ 求解仍保持了相同的精度阶次，但离散化后的输运方程的非线性性质得到了本质上的降低，各时间步长内的收敛性得到了改善。

Frozen Flux Formulation选项可从Solution Method对话框中访问。

注：此选项仅适用于使用压力基迭代求解器且不使用移动/变形网格模型的单相瞬态问题。

24.4.5.2 无迭代时间推进方式

迭代时间推进方式的每个时间步长都要进行大量的外部迭代，因此需要相当大的计算工作量。无迭代时间推进(Non-Iterative Time-Advancement，NITA)方式的基本思想为：要保证整体时间精度，实际上并不需要将分裂误差降至零，而只需使其与截断误差具有相同的精度阶数。如图所示，NITA方法不需要外部迭代，每个时间步长只进行一次外部迭代，这大大加快了瞬态模拟的速度。然而，NITA格式仍然允许内部迭代来求解单独的方程组。

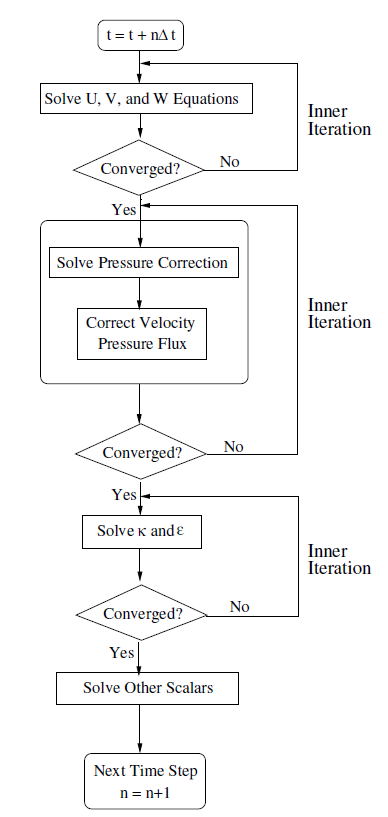
对于单相流，Fluent提供了两种版本的NITA方法：无迭代分步法 (non-iterative fractional step method，FSM)及无迭代PISO方法。两种NITA方法均可用于一阶和二阶时间积分。

对于欧拉多相流，Fluent提供了non-iterative PC Simple方法。无迭代PC Simple是PC Simple和PISO格式的混合体。

注：一般情况下，NITA求解器不建议用于高粘性流体流动；对于流体密度强烈依赖于组分浓度的流动，不推荐使用NITA求解器。

24.4.6 动量方程离散的修正形式

本节介绍将校正形式应用于离散化动量方程的背景。

Fluent默认情况下启用离散化动量方程的修正形式（并且可以使用TUI命令solve/set/advanced/correction-form进行禁用，该TUI命令将在未来的版本中删除）。

将守恒律 (通常称为运输方程) 离散化，得出迭代的线性方程组，其形式如下： $$ {a_{p} \varphi_{p}^{n}=\sum_{n b} a_{n b} \varphi_{n b}^{n}+b_{p}}\tag{24.71}\label{24.71} $$ 这里 $φ_{i}$ 是传输的可变单元值， $a_{nb}$ 是相邻网格的耦合系数， $a_{p} = \sum_{nb} a_{nb}$ 和 $b_{p}$ 为网格源项。在不失去通用性的情况下，这是在没有欠松弛和瞬态项的情况下写的。

通过将从迭代 $n - 1$ 到迭代 $n$ 的校正定义为：

$$ {\delta \varphi_{k}^{n}=\varphi_{k}^{n}-\varphi_{k}^{n-1}}\tag{24.72}\label{24.72} $$ 方程$\eqref{24.71}$可写成： $$ {a_{p} \delta \varphi_{p}^{n}=\sum_{n b} a_{n b} \delta \varphi_{n b}^{n}+b_{p}-\left(a_{p} \varphi_{p}^{n-1}-\sum_{n b} a_{n b} \varphi_{n b}^{n-1}\right)}\tag{24.73}\label{24.73} $$ 此方程称之为离散方程的校正形式（或增量形式）。