Ansys Fluent 中的密度基求解器将连续性、动量以及在适当情况下能量和物种传输的控制方程同时求解为一组或向量形式的方程。对于其他标量，控制方程将按顺序（即相互分离并与耦合集分离）求解，具体方式在“通用标量传输方程：离散化和求解”（第964页）中描述。针对耦合方程组，提供了两种求解算法：耦合显式公式和耦合隐式公式。

23.5.1 向量形式的控制方程

描述单组分流体平均流动特性的控制方程系统，以积分笛卡尔形式表示，针对具有微分表面积 $d A$ 的任意控制体积 $V$ ，如下所示：

$\frac{\partial}{\partial t} \int_{V} W d V + \oint [F - G] \cdot d A = \int_{V} H d V (23.74)$

向量 ( W )、( F ) 和 ( G ) 定义如下：

$W = ⎩ ⎨ ⎧ ρ ρ u ρ v ρw ρE ⎭ ⎬ ⎫, F = ⎩ ⎨ ⎧ ρ v ρ vu + p  ρ vv + p  ρ v w + p k ρ v E + p v ⎭ ⎬ ⎫, G = ⎩ ⎨ ⎧ 0 τ_{x i} τ_{y i} τ_{z j} τ_{ij} v_{j} + q ⎭ ⎬ ⎫ (23.75)$

向量 $H$ 包含了诸如体力与能量源等源项。

这里， $ρ$ 、 $v$ 、 $E$ 和 $p$ 分别表示流体的密度、速度、单位质量的总能量和压力。 $τ$ 是粘性应力张量， $q$ 是热流。

总能量 $E$ 与总焓 $H$ 通过以下关系相联系：

$E = H - p / ρ (23.76)$

这里

$H = h + ∣ v ∣^{2} /2 (23.77)$

由于流体速度 $v$ 与声速 $c$ （音速）之间的差异，如公式 23.74（第 995 页）所示的纳维-斯托克斯方程在低马赫数时会变得（数值上）非常刚性。对于不可压缩流动，无论流体速度如何，情况也是如此，因为在不可压缩流体中，声波传播速度无限快（音速为无限大）。在这些条件下，方程的数值刚性导致收敛速度不佳。在 Ansys Fluent 的密度基求解器中，通过采用一种称为（时间导数）预处理的技术 [698]（第 1097 页）克服了这一困难。

23.5.2 预处理

时间导数预处理通过用预处理矩阵预乘公式 23.74（第 995 页）中的时间导数项来修改该项。这样做的效果是重新调整所求解方程组中的声速（特征值），以缓解在低马赫数和不可压缩流动中遇到的数值刚性问题。

预处理矩阵的推导首先通过链式法则将公式 23.74（第 995 页）中的因变量从守恒量 $W$ 转换为原始变量 $Q$ ，如下所示：

$\frac{\partial W}{\partial Q} \frac{\partial}{\partial t} \int_{V} Q d V + \oint [F - G] \cdot d A = \int_{V} H d V (23.78)$

其中， $Q$ 是向量 ${p, u, v, w, T}^{T}$ ，而雅可比矩阵 $\partial W / \partial Q$ 则由以下给出。

$\frac{\partial W}{\partial Q} = ρ_{p} ρ_{p} u ρ_{p} v ρ_{p} w ρ_{p} H - δ 0 ρ 00 ρ u 00 ρ 0 ρ v 000 ρ ρw ρ_{T} ρ_{T} u ρ_{T} v ρ_{T} w ρ_{T} H + ρ C_{p} (23.79)$

以下文本翻译成中文：

在哪里

$ρ_{p} = \frac{\partial ρ}{\partial p}_{T}, ρ_{T} = \frac{\partial ρ}{\partial T}_{p} (23.80)$

对于理想气体， $δ = 1$ ，而对于不可压缩流体， $δ = 0$ 。

选择原始变量 $Q$ 作为因变量有若干原因。首先，在求解不可压缩流动时，这是一个自然的选择。其次，当我们使用二阶精度时，为了在粘性通量中获得更准确的的速度和温度梯度，以及在无粘通量中获得压力梯度，我们需要重建 $Q$ 而不是 $W$ 。最后，选择压力作为因变量使得系统中声波的传播可以被单独识别[670]（第1096页）。

我们通过用预处理矩阵 $Γ$ 替换雅可比矩阵 $\partial W / \partial Q$ （方程23.79，第996页）来预处理系统，从而使得预处理的系统以守恒形式变为

$Γ \frac{\partial}{\partial t} \int_{V} Q d V + \oint [F - G] \cdot d A = \int_{V} H d V (23.81)$

此处

$Γ = θ θ u θ v θw θ H - δ 0 ρ 00 ρ u 00 ρ 0 ρ v 000 ρ ρw ρ_{T} ρ_{T} u ρ_{T} v ρ_{T} w ρ_{T} H + ρ C_{p} (23.82)$

参数 $Θ$ 由以下公式给出：

$θ = (\frac{1}{U _{r}^{2}} - \frac{ρ _{T}}{ρ C _{p}}) (23.83)$

方程23.83（第996页）中出现的参考速度 $U_{r}$ 是局部选择的，以确保系统的特征值在关于对流和扩散时间尺度方面保持良好的条件[698]（第1097页）。

经过预处理的系统（方程23.81（第996页））的特征值结果为

$u, u, u, u^{'} + c^{'}, u^{'} - c^{'} (23.84)$

哪里

$u = v \cdot n$

$u^{'} = u (1 - α)$

$c^{'} = α^{2} u^{2} + U_{r}^{2}$

$α = (1 - β U_{r}^{2}) /2$

$β = (ρ_{p} + \frac{ρ _{T}}{ρ C _{p}})$

对于理想气体， $β = (γ RT)^{- 1} = 1/ c^{2}$ 。因此，当 $U_{r} = c$ （在音速及以上）， $α = 0$ ，预处理系统的特征值采用传统形式，即 $u \pm c$ 。然而，在低速情况下，随着 $U_{r} \to 0$ ， $α \to 1/2$ ，所有特征值都与 $u$ 同阶。对于常密度流动， $β = 0$ 且 $α = 1/2$ ，无论 $U_{r}$ 的值如何。只要参考速度与当地速度同阶，所有特征值都保持在 $u$ 的阶数。因此，预处理系统的特征值在所有速度下都保持良好的条件。

请注意，通过将 $1/ U_{r}^{2}$ 设为 $ρ_{p}$ ，即密度对压力的导数，可以从方程23.81（第996页）精确恢复未预处理的纳维-斯托克斯方程。在这种情况下， $Γ$ 精确简化为雅可比矩阵 $\partial W / \partial Q$ 。

尽管方程23.81（第996页）在稳态是守恒的，但在严格意义上，对于时间相关流动并不守恒。然而，这并不是问题，因为预处理已经破坏了方程的时间精度，我们不会以这种形式将其用于非定常计算。

对于非定常计算，当使用双时间步进方法时（隐式时间步进（双时间步进公式）（第1002页）），可以使用非定常预处理。非定常预处理通过改善人工耗散的缩放来提高解的精度，并通过优化每个物理时间步所需的子迭代次数来最大化效率[504]（第1086页）。特别是对于低马赫数流动，无论是低频问题（大时间步长）还是高频问题（小时间步长），与未预处理的情况相比，都有可能在计算时间上实现显著节省。

不稳定的预处理根据用户指定的时间步长以及流动的局部对流和声学时间尺度来调整预处理的级别。对于声学问题，物理时间步长较小，因为它基于声学CFL数。在这种情况下，预处理参数 $U_{r}^{2}$ 将接近 $c^{2}$ ，这实际上将几乎完全关闭低马赫数预处理。对于以对流为主导的问题，如湍流涡旋结构的传输等，物理时间步长较大，因为它基于粒子CFL数。相应的非定常预处理参数 $U_{r}^{2}$ 将接近 $u^{2}$ ，这对应于定常预处理选择。对于中间的物理时间步长，非定常预处理参数将被调整以提供伪时间迭代的最佳收敛效率和人工耗散项的准确缩放，无论物理时间步长的选择如何。

23.5.3 对流通量

23.5.3.1 Roe 通量差分分裂方案

方程 23.81（第 996 页）中出现的无粘通量向量 $F$ 是通过标准的迎风通量差分分裂 [559]（第 1089 页）来评估的。这种方法承认通量向量 $F$ 包含根据系统特征值传播的速度和方向通过域的特征信息。通过将 $F$ 分成部分，每个部分包含朝特定方向传播的信息（即特征信息），并以与其相应特征值一致的方式对分裂的通量进行迎风差分，我们得到每个面上的离散通量的以下表达式：

$F = \frac{1}{2} (F_{R} + F_{L}) - \frac{1}{2} Γ A δ Q (23.85)$

这里， $δ Q$ 表示空间差值 $Q_{R} - Q_{L}$ 。通量 $F_{R} = F (Q_{R})$ 和 $F_{L} = F (Q_{L})$ 是利用面“右侧”和“左侧”的（重构的）解向量 $Q_{R}$ 和 $Q_{L}$ 计算得到的。矩阵 $A$ 则定义为

$A = M ∣ Λ ∣ M^{- 1} (23.86)$

其中， $Λ$ 是特征值的对角矩阵， $M$ 是将对角化 $Γ^{- 1} A$ 的模态矩阵，其中 $A$ 是无粘通量雅可比矩阵 $\partial F / \partial Q$ 。

对于非预处理系统（以及理想气体），当使用 Roe 平均值来评估 $Γ A$ 时，方程 23.85（第 998 页）简化为 Roe 通量差分分裂法 [559]（第 1089 页）。目前，使用状态 $Q_{R}$ 和 $Q_{L}$ 的算术平均。

在其当前形式下，方程 23.85（第 998 页）可以被视为二阶中心差分加上一个附加的矩阵耗散项。这个附加的矩阵耗散项不仅负责对对流变量、超音速流动中的压力和通量速度进行上风处理，而且还提供了低速和不可压缩流动稳定性和高效收敛所需的压速耦合。

23.5.3.2 AUSM+ 方案

计算方程 23.81（第 996 页）中出现的通量向量 $F$ 的另一种方法是使用通量向量分裂方案 [107]（第 1063 页）。该方案，称为对流上游分裂方法（AUSM），由 Liou 和 Steffen 在 1993 年首次提出 [381]（第 1079 页）。AUSM 方案首先根据相邻单元的特征速度计算单元界面的马赫数。然后使用界面马赫数来确定无粘通量对流部分的上风外推。压力项使用单独的马赫数分裂。Liou [380]（第 1079 页）提出了基于广义马赫数的对流和压力分裂函数，新方案被称为 AUSM+。AUSM+ 方案具有几个理想的特性：

精确分辨接触和冲击不连续性
保持标量量的正值
在静止和移动冲击中无振荡

AUSM+ 格式通过提出一种形式的数值通量，避免了使用显式的人工耗散：

$F = m_{f} φ + p_{i} (23.87)$

这里， $m_{f}$ 是通过界面的质量通量，它是使用界面左右两侧马赫数的四阶多项式函数计算得出的。

Ansys Fluent采用基于低马赫数预处理的AUSM+方案的全速版本。

23.5.3.3 低扩散Roe通量差分分裂方案

为了减少LES计算中的耗散，Ansys Fluent使用了一种改进版的Roe通量差分分裂方案，称为低扩散Roe通量差分分裂方案。该方案包括低马赫数预处理，其中通过使用结合中心方案和二阶迎风方案（Roe的通量差分方案）的混合方案，人工耗散项已被减少[87]（第1062页）。

在选择LES粘性模型并使用隐式时间格式（双时间步进）的特殊情况下，可以使用低扩散Roe-FDS。建议在选择此通量方案时使用二阶迎风方案以获得最大精度。

重要提示：低扩散离散化仅适用于亚音速流动。对于高马赫数流动，建议切换到标准Roe-FDS或AUSM+通量方案以及二阶迎风离散化。

重要提示：在使用显式时间格式的LES运行时，低扩散Roe-FDS不可用，您需要使用标准Roe-FDS或AUSM+通量方案以及二阶迎风离散化。

要了解如何应用不同的对流通量，请参阅用户指南中的对流通量类型。

23.5.4 稳态流动求解方法

在Ansys Fluent中，控制方程组（方程23.81，第996页）在时间上被离散化，适用于稳态和非稳态计算。在稳态情况下，假设时间推进进行直到达到稳态解。耦合方程的时间离散化通过隐式或显式时间推进算法来实现。下面将介绍这两种算法。要了解如何应用这两种公式，请参阅用户指南中的密度基求解器设置。

23.5.4.1 显式公式

在显式方案中，使用多级时间步进算法[277]（第1073页）来离散化方程23.81（第996页）中的时间导数。解从迭代 $n$ 推进到迭代 $n + 1$ ，采用 $m$ 级Runge-Kutta方案，具体如下：

$Q^{0} = Q^{n}$

$Δ Q^{i} = - α_{i} Δ t Γ^{- 1} R^{i - 1}$

$Q^{n + 1} = Q^{m}$

其中， $Δ Q^{i} \equiv Q^{i} - Q^{n}$ ， $i = 1, 2, \dots, m$ 表示 $m$ 阶段方案的阶段计数器。 $α_{i}$ 是第 $i^{t h}$ 阶段的多元系数。残差 $R^{i}$ 根据中间解 $Q^{i}$ 计算得出，对于公式 23.81（第 996 页），其表达式为

$R^{i} = \sum N_{faces} (F (Q^{i}) - G (Q^{i})) \cdot A - V H (23.88)$

时间步长 $Δ t$ 是根据 CFL（Courant-Friedrichs-Lewy）条件计算得出的。

$Δ t = \frac{2 CFL V}{f \sum λ _{f}^{m a x} A _{f}} (23.89)$

其中， $V$ 表示单元体积， $A_{f}$ 是面面积，而 $λ_{f}^{m a x}$ 则是由方程 23.84（第 997 页）定义的局部特征值的最大值。

对于稳态解，显式格式的收敛加速可以通过使用局部时间步进、残差平滑和全近似存储多重网格来实现。

局部时间步进是一种方法，通过这种方法，每个控制体积的解根据由时间步进方案的局部稳定性极限定义的单元时间步长在时间上前进。

另一方面，残差平滑增加了时间步进方案的稳定性极限界限，从而允许使用更大的 CFL 值来实现快速收敛（隐式残差平滑（第 1000 页））。

显式方案的收敛速度可以通过使用全近似存储（FAS）多重网格方法来加速，该方法在全近似存储（FAS）多重网格（第 1018 页）中描述。

默认情况下，Ansys Fluent 对于使用基于密度显式求解器的稳态流动，采用基于 Lynn [402]（第 1080 页）工作的三阶段 Runge-Kutta 方案。

23.5.4.1.1 隐式残差平滑

通过增加方案的支持，通过与邻居的残差进行隐式平均，可以进一步增加最大时间步长。残差通过拉普拉斯平滑算子进行滤波：

$\overset{ˉ}{R}_{i} = R_{i} + ε \sum (\overset{ˉ}{R}_{j} - \overset{ˉ}{R}_{i}) (23.90)$

这个方程可以通过以下雅可比迭代法求解：

$\overset{ˉ}{R}_{i}^{m} = \frac{R _{i} + ϵ 1 \sum N R ˉ _{j}^{m - 1}}{1 + ϵ N} (23.91)$

其中 $N$ 表示邻点的数量。通常情况下，进行两次雅可比迭代就足以使时间步长翻倍，取值 $ε = 0.5$ 即可。

23.5.4.2 隐式格式

在隐式方案中，控制方程（公式 23.81，第 996 页）的时间欧拉隐式离散化与通量的牛顿型线性化相结合，产生了以下以增量形式表示的线性化系统 [696]（第 1097 页）：

$[D + j \sum N_{faces} S_{j, k}] Δ Q^{n + 1} = - R^{n} (23.92)$

中心和对角系数矩阵， $D$ 和 $S_{j, k}$ 由以下给出：

$D = \frac{V}{Δ t} Γ + j \sum N_{faces} S_{j, i} (23.93)$

$$ {S}{j, k} = \left( {\frac{\partial {F}{j}}{\partial {Q}{k}} - \frac{\partial {G}{j}}{\partial \tag{23.74}{Q}{k}}}\right) {A}{j}\tag{23.94} $$

残差向量 $R^{n}$ 和时间步长 $Δ t$ 分别按照方程 23.88（第 1000 页）和方程 23.89（第 1000 页）定义。

方程 23.92（第 1001 页）默认采用不完全下上分解（ILU）或对称点高斯-赛德尔算法求解，结合针对耦合方程组适配的代数多重网格（AMG）方法（参见代数多重网格（AMG）（第 1013 页））。

显式松弛可以改善隐式公式收敛到稳态的性能。默认情况下，隐式求解器启用显式松弛，并使用 0.75 的因子。您可以指定一个因子 $α$ ，以控制代数多重网格（AMG）周期结束后解向量 $Q$ 在迭代间的变化量。

$Q_{new} = Q_{old} + α Δ Q (23.95)$

通过指定一个小于默认值1的 $α$ 值，解向量中的变量将进行欠松弛处理，从而改善收敛历史。有关如何设置此值的信息，请参阅用户指南中的“指定显式松弛”部分。

重要提示：请注意，显式松弛仅适用于稳态模式下的基于密度的隐式求解器。

23.5.4.2.1. 针对拉伸网格的收敛加速

当在包含高度拉伸单元（通常在近壁边界处发现的高纵横比单元）的网格上求解流动时，传统的隐式求解方法会因方程 Equation 23.89（第1000页）定义的局部时间步长值过小而导致收敛速度减慢。单元纵横比越大，局部时间步长越小，解的局部变化速率越慢。方程 Equation 23.89（第1000页）中的时间步长定义实际上基于单元的最小特征距离。对于隐式求解方法，一个更优的时间步长定义可以基于单元的最大特征长度 [364]（第1078页），从而给出新的时间步长定义：

$Δ t = \frac{2 CFL _{V} V _{A R}}{f \sum λ _{f}^{m a x} A _{f}} (23.96)$

其中，AR是单元纵横比，定义为单元的最大长度与最小长度之比，即 $A R = \frac{l _{m a x}}{l _{m i n}}$ 。

实际上，新的定义将根据单元纵横比的值，使局部CFL值在不同单元之间按比例变化。当单元纵横比接近1时，局部CFL值将与您输入的值相似。另一方面，在高纵横比拉伸单元上，局部CFL值是单元纵横比的倍数。新的时间步长定义将加速解收敛，特别是在 $Y +$ 接近1的网格上。

23.5.5 非定常流动求解方法

对于时间精确计算，提供了显式和隐式时间步进方案。（隐式时间步进方法也称为“双时间步进”。）

23.5.5.1 显式时间步进

显式时间步进方法仅适用于显式格式中描述的显式方案（参见显式格式，第1000页）。时间步长由CFL条件确定。为了保持解的时间精度，显式时间步进在域的每个单元中采用相同的时间步长（这也称为全局时间步长），并且在禁用预处理的情况下。默认情况下，Ansys Fluent对非定常流动使用四级Runge-Kutta方案。

23.5.5.2 隐式时间步进（双时间格式）

隐式时间步进方法（也称为双时间格式）在密度基的显式和隐式格式中都可用。

在进行隐式时间步进（双时间步进）的非定常模拟时，Ansys Fluent使用低马赫数时间导数非定常预处理方法，以在纯对流过程（例如模拟非定常湍流）和声学过程（例如模拟波传播）中提供准确结果[661]（第1095页），[504]（第1086页）。

在此，我们向方程23.74（第995页）引入一个预处理伪时间导数项，具体如下：

$\frac{\partial}{\partial t} \int_{V} W d V + Γ \frac{\partial}{\partial τ} \int_{V} Q d V + \oint_{V} [F - G] \cdot d A = \int_{V} H d V (23.97)$

其中， $t$ 表示物理时间， $τ$ 是在时间推进过程中使用的一种伪时间。注意，当 $τ \to \infty$ 时，方程 23.97（第 1002 页）左侧的第二项消失，从而恢复方程 23.74（第 995 页）。

方程 23.97（第 1002 页）中的时间相关项通过采用一阶或二阶精度的隐式后向时间差分进行离散化。

双时间步格式以半离散形式表示如下：

$[\frac{Γ}{Δ τ} + \frac{ε _{0}}{Δ t} \frac{\partial W}{\partial Q}] Δ Q^{k + 1} + \frac{1}{V} \oint [F - G] \cdot d A = H - \frac{1}{Δ t} (ε_{0} W^{k} - ε_{1} W^{n} + ε_{2} W^{n - 1}) (23.98)$

当 ${ε_{0} = ε_{1} = 1/2, ε_{2} = 0}$ 时，可获得一阶时间精度，而 ${ε_{0} = 3/2, ε_{1} = 2, ε_{2} = 1/2}$ 则可获得二阶时间精度（请注意，这是针对固定时间步长公式的；对于可变时间步长公式，请参见公式 23.27 (第 975 页))。 $k$ 是内部迭代计数器， $n$ 表示任意给定的物理时间层。

通过使用隐式或显式时间推进算法的一系列内部迭代，伪时间导数在每个物理时间层被驱动至零。

在整个伪时间（内部）迭代过程中， $W^{n}$ 和 $W^{n - 1}$ 保持不变， $W^{k}$ 从 $Q^{k}$ 计算得出。随着 $τ \to \infty$ ，下一个物理时间层的解 $W^{n + 1}$ 由 $W (Q^{k})$ 给出。

请注意，物理时间步长 $Δ t$ 仅受所需时间精度水平的限制。伪时间步长 $Δ τ$ 由（隐式或显式）时间推进方案的 CFL 条件决定。

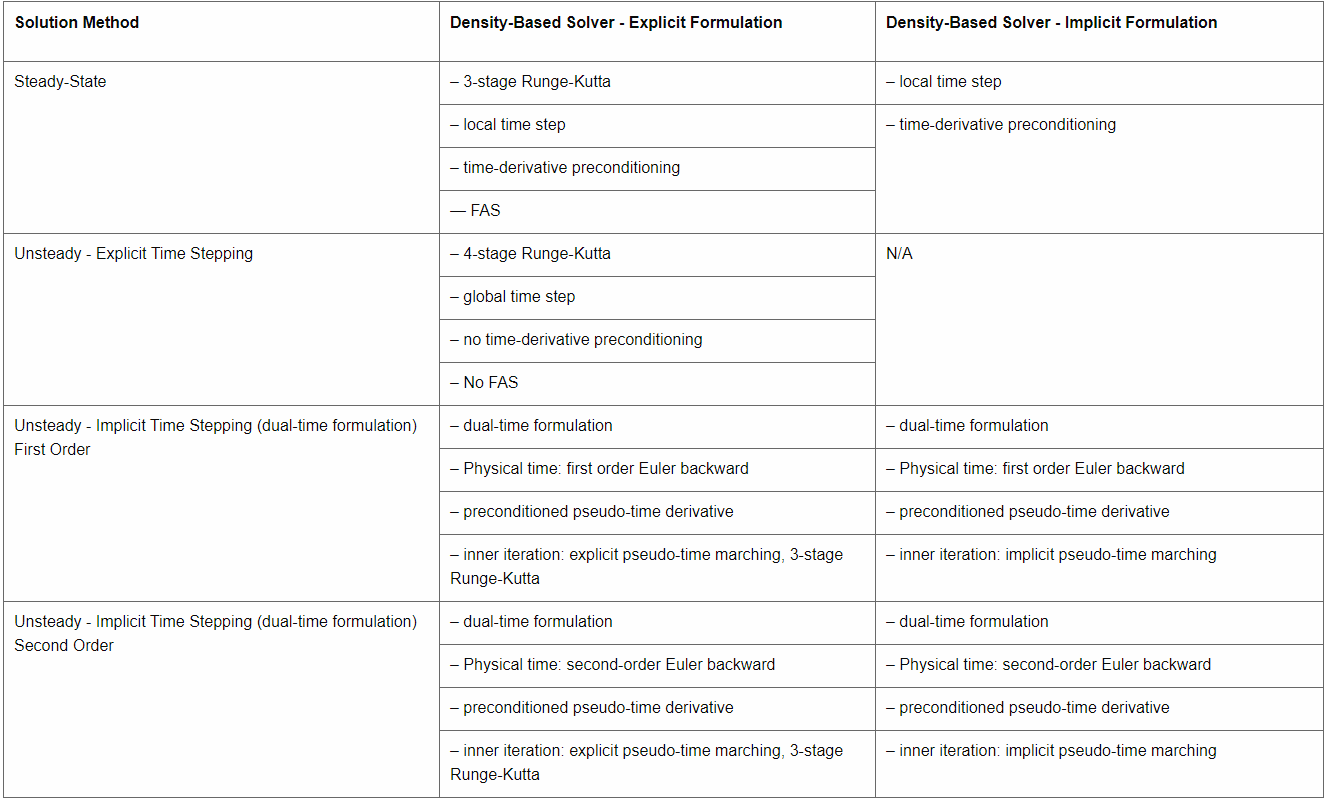
表 23.1：密度基求解器总结（第 1003 页）概述了从稳态计算中的迭代方案到瞬态计算中的时间推进方案的密度基求解器的所有操作模式。

表 23.1：密度基求解器总结