采用运动参考系的主要目的是将原本在静止（惯性）坐标系中非定常的问题，转换为相对于运动坐标系的定常问题。对于匀速运动的参考系（例如，旋转速度恒定），可以将流体运动方程变换到该运动参考系中，从而可能获得稳态解。此外，值得注意的是，即使在具有恒定旋转速度的运动参考系中，也可以进行非定常模拟。这在需要模拟某些现象时是必要的，比如从旋转风扇叶片上脱落的涡旋。此种情况下的非定常性源于流体的自然不稳定性（涡旋生成）而非与静止部件相互作用所致。

在Fluent中，还可以实现具有非定常平移和旋转速度的参考系运动。同样地，适当的加速度项会被添加到流体运动的方程中。由于参考系运动的非定常性，这类问题相对于运动参考系而言本质上是非定常的。

2.2.1. 运动参考系的方程

考虑一个相对于静止（惯性）参考系以线速度 $v_{t}$ 平移并绕角速度 $ω$ 旋转的坐标系，如图2.3所示：静止与运动参考系（第21页）。运动系统的原点由位置矢量 $r_{0}$ 定位。

图2.3：静止与运动参考系

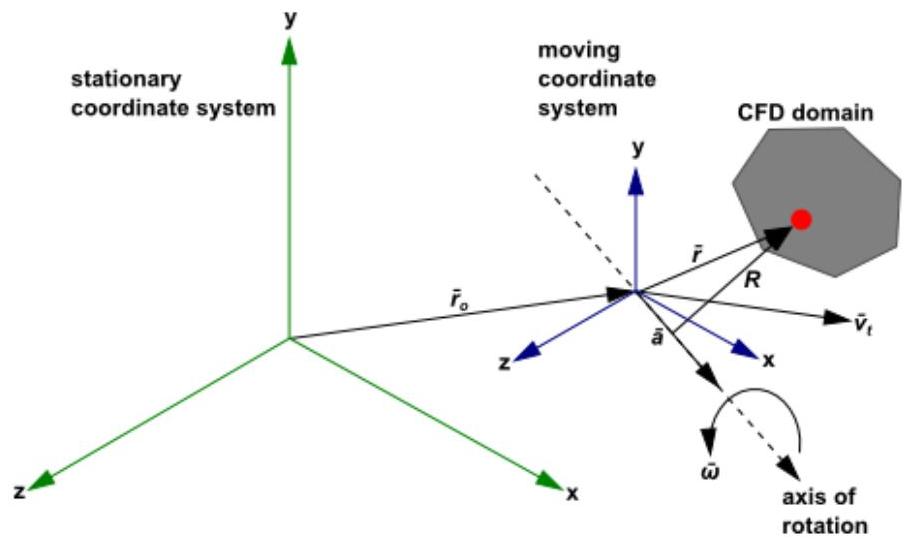
旋转轴由单位方向向量 $a$ 定义，使得

$ω = ω a (2.1)$

CFD问题的计算域是相对于运动坐标系定义的，使得CFD域中的任意一点可以通过从运动坐标系的原点出发的位置矢量 $r$ 来定位。

流体速度可以通过以下关系从静止坐标系转换到运动坐标系：

$v_{r} = v - u_{r} (2.2)$

where

$u_{r} = v_{t} + ω \times r (2.3)$

在上面的方程中， $v_{r}$ 表示相对速度（从运动参考系观察到的速度）， $v$ 是绝对速度（从静止参考系观察到的速度）， $u_{r}$ 是运动参考系相对于惯性参考系的速度， $v_{t}$ 是平移参考系的速度，而 $ω$ 则是角速度。需要注意的是， $ω$ 和 $v_{t}$ 都可能是时间的函数。

在运动参考系中求解运动方程时，流体的加速度会因动量方程中出现的额外项而增加[47]（第1059页）。此外，这些方程可以用两种不同的方式来表述：

使用相对速度作为因变量来表达动量方程（称为相对速度公式）。
在动量方程中使用绝对速度作为因变量来表达（称为绝对速度公式）。

这两种公式的控制方程将在下文中提供。需要注意的是，Fluent的压力基求解器提供了选择其中任一公式的选项，而密度基求解器则始终采用绝对速度公式。关于每种速度公式的优势的更多信息，请参阅用户指南中的“选择相对或绝对速度公式”部分。

2.2.1.1. 相对速度公式

在相对速度公式中，运动参考系中流体流动的控制方程可以写成如下形式：

质量守恒：

$\frac{\partial ρ}{\partial t} + \nabla \cdot ρ v_{r} = 0 (2.4)$ 动量守恒： $\frac{\partial}{\partial t} (ρ ν_{r}) + \nabla \cdot (ρ ν_{r} ν_{r}) + ρ (2 ω \times ν_{r} + ω \times ω \times r + α \times r + a) = - \nabla p + \nabla \cdot \overline{τ}_{r} + F (2.5)$

式中， $α = \frac{d ω}{d t}$ ， $a = \frac{d v _{t}}{d t}$

能量守恒：

$\frac{\partial}{\partial t} (ρ E_{r}) + \nabla \cdot (ρ v_{r} H_{r}) = \nabla \cdot (k \nabla T + \overline{\overset{τ}{ˉ}}_{r} \cdot v_{r}) + S_{h} (2.6)$

动量方程包含四个额外的加速度项。前两项分别是科里奥利加速度 $(2 ω \times v_{r})$ 和向心加速度 $(ω \times ω \times r)$ 。这些项在稳定运动的参考系（即，角速度和线速度恒定）和加速参考系（即，角速度和/或线速度随时间变化）中都会出现。第三和第四项分别是由旋转速度和线性速度的非稳态变化引起的。对于恒定的平移和/或旋转速度，这些项消失。此外，粘性应力 $(\overline{\overset{τ}{ˉ}}_{r})$ 与公式 $1.4 (p .3)$ 相同，只是使用了相对速度导数。能量方程以相对内能 $(E_{r})$ 和相对总焓 $(H_{r})$ （也称为转焓）表示。这些变量定义为：

$E_{r} = h - \frac{p}{ρ} + \frac{1}{2} (v_{r}^{2} - u_{r}^{2}) (2.7)$

$H_{r} = E_{r} + \frac{p}{ρ} (2.8)$

2.2.1.2 绝对速度公式

在绝对速度公式中，对于一个稳定运动的参考系，流体流动的控制方程可以写成如下形式：

质量守恒：

$\frac{\partial ρ}{\partial t} + \nabla \cdot ρ v_{r} = 0 (2.9)$

动量守恒：

$\frac{\partial}{\partial t} ρ v + \nabla \cdot (ρ v_{r} v) + ρ [ω \times (v - v_{t})] = - \nabla p + \nabla \cdot \overset{τ}{ˉ} + F (2.10)$

能量守恒：

$\frac{\partial}{\partial t} ρE + \nabla \cdot (ρ v_{r} H + p u_{r}) = \nabla \cdot (k \nabla T + \overline{\overset{τ}{ˉ}} \cdot v) + S_{h} (2.11)$

在这种表述中，科里奥利加速度和向心加速度可以简化为一个单一项 $([ω \times (v - v_{t})])$ 。需要注意的是，绝对速度方程的动量表达式中不包含任何显式的涉及 $α$ 或 $a$ 的项。

2.2.1.3. 参考坐标系运动的相对指定

Fluent允许您相对于一个已经运动（旋转和平移）的参考坐标系来指定运动参考系。在这种情况下，最终的速度矢量是根据这个相对运动计算得出的。

$v_{r} = v - u_{r} (2.12)$

式中

$u_{r} = u_{r 1} + u_{r 2} (2.13)$

以及

$ω = ω_{1} + ω_{2} (2.14)$

方程2.13（第23页）被称为伽利略变换。

旋转矢量如同方程2.14（第23页）所示相加，因为参考系的运动可以视为刚体旋转，其中每个点的旋转速率是恒定的。此外，这允许将旋转表述为角速度轴向（也称为伪）矢量，描述瞬时无穷小的变换。在这种情况下，两个旋转速率都遵循交换律。需要注意的是，这种方法在处理有限旋转时是不够的。在这种情况下，基于欧拉角的旋转矩阵公式是必要的[544]（第1088页）。

要学习如何在另一个运动参考系内指定一个运动参考系，请参阅用户指南中的“设置多个参考系”部分。