在三维域中的二维薄膜质量守恒方程为：

$$\frac{\partial {\rho }_{l}h}{\partial t}+{\nabla }_s\cdot \left({\rho }_{l}h{\overrightarrow{V}}_l\right)={\dot{m}}_s\text{\hspace{1em}(17.1)}$$

液膜动量守恒表达如下：其中，${\rho }_l$ 表示液体密度，$h$ 代表液膜高度，${\nabla }_s$ 是表面梯度算子，${\overrightarrow{V}}_l$ 为液膜平均速度，而 ${\dot{m}}_s$ 则是由于液滴收集、液膜分离、液膜剥离以及相变等因素导致的单位壁面面积上的质量源。

$$\frac{\partial {\rho }_{l}h{\overrightarrow{V}}_l}{\partial t}+{\nabla }_s\cdot \left({\rho }_{l}h{\overrightarrow{V}}_l{\overrightarrow{V}}_l+{\bar{D}}_V\right)=-h{\nabla }_s{P}_L+{\rho }_{l}h{\overrightarrow{g}}_{\tau }+\frac{3}{2}{\overrightarrow{\tau }}_{fs}-\frac{3{\mu }_l}{h}{\overrightarrow{V}}_l+{\dot{\overrightarrow{q}}}_s+{\overrightarrow{\tau }}_{{\theta }_w}\text{\hspace{1em}(17.2)}$$

式中

$$P_L=P_{gas}+P_h+P_{\sigma }$$

$$P_h=-\rho h\left(\overrightarrow{n}\cdot \overrightarrow{g}\right)$$

$$P_{\sigma }=-\sigma {\nabla }_s\cdot \left({\nabla }_{s}h\right)$$

方程17.2（第838页）左侧的各项分别表示瞬态和对流效应，其中张量${\overline{\bar{D}}}_V$表示基于二次薄膜速度分布计算的微分对流项[287]（第1073页），[288]（第1073页）。右侧第一项包括气流压力、垂直于壁面的重力分量（称为扩散）和表面张力的影响；第二项表示沿薄膜方向的重力效应；第三和第四项基于二次薄膜速度分布表示了气体-薄膜和薄膜-壁面界面上的净粘性剪切力；第五项与液滴收集或分离有关；最后一项是由于薄膜液体表面张力和接触角产生的表面力。请注意，在得出右侧的剪切和粘性项时，假设了抛物线型的薄膜速度分布。

薄膜能量的守恒表示为：

$$\frac{\partial {\rho }_{l}h{T}_f}{\partial t}+{\nabla }_s\cdot \left({\rho }_{l}h{T}_f{\overrightarrow{V}}_l+{\overrightarrow{D}}_T\right)=\frac{1}{C_p}\left[\frac{2k_f}{h}\left(T_s+T_w-2T_m\right)+{\dot{q}}_{imp}+{\dot{m}}_{vap}L\right]\text{\hspace{1em}(17.3)}$$

在上式中，$T_f$ 是平均薄膜温度，向量 ${\overrightarrow{D}}_T$ 是使用二次薄膜速度和温度分布表示计算的微分平流项。在右侧括号内的第一项表示气体-薄膜和薄膜-壁面界面上的净热通量，$T_s$ 和 $T_w$ 分别为薄膜表面和壁面温度，$T_m$ 为薄膜半深度温度，均从薄膜温度分布表示和气体-薄膜及薄膜-壁面界面的热边界条件计算得出。${\dot{q}}_{imp}$ 是由于液体从主流流到壁面的冲击而产生的源项。${\dot{m}}_{vap}$ 是质量蒸发或凝结速率，$L$ 是与相变相关的潜热。

公式17.1（第838页）和公式17.2（第838页）构成了EWF模型的基础，只有在需要进行热模型时，才可选解公式17.3（第839页）。这些方程在壁面边界的表面上求解。由于这里考虑的薄膜很薄，润滑近似（平行流）是有效的，因此这些方程在平行于表面的局部坐标系中求解。

后续部分介绍了在Ansys Fluent中采用的EWF子模型和数值求解程序。

17.2.1 薄膜子模型

欧拉壁膜模型可以通过源项与离散相模型（DPM）、VOF多相模型以及欧拉多相模型进行交互。在与DPM模型交互时，离散颗粒被收集形成壁膜。离散颗粒在与膜边界交互时会发生溅射，产生额外的颗粒，这与拉格朗日膜模型中描述的方式相同。当膜从壁面分离或剪切应力足够大以至于大颗粒可以从膜上剥离时，也会产生额外的颗粒。通过向膜方程添加源项来考虑因分离或剥离而从膜表面离开的质量。在欧拉多相交互中，多相流中的次要相在固体表面上被捕获，形成液膜。可以计算固体表面的收集效率。由于分离和剥离而从液膜中离开的质量和动量被添加到多相流中的次要相。在与VOF多相模型交互时，超过指定限度的膜液体可以使用VOF模型进行建模，而在VOF多相流中体积小于指定限度的次要相流体可以使用壁膜模型进行建模。

17.2.1.1 DPM收集

离散颗粒流或撞击壁面边界的离散颗粒被吸收到膜中。当颗粒被吸收时，它们的质 量和动量被添加到方程17.1（第838页）和方程17.2（第838页）的源项中，分别是连续性和动量方程。质量源项由下式给出：

$${\dot{m}}_s={\dot{m}}_p\text{\hspace{1em}(17.4)}$$

其中，${\dot{m}}_p$ 表示撞击表面的颗粒流的流量。动量源项即为

$${\dot{\overrightarrow{q}}}_s={\dot{\mathrm{m}}}_p\cdot \left({\overrightarrow{V}}_p-{\overrightarrow{V}}_l\right)\text{\hspace{1em}(17.5)}$$

其中 ${\overrightarrow{V}}_p$ 表示颗粒流的流速，${\overrightarrow{V}}_l$ 表示液膜的流速。

17.2.1.2 颗粒与壁面相互作用

颗粒撞击液膜壁面边界可能导致颗粒反弹、飞溅或被吸收形成壁面液膜。颗粒与壁面边界的相互作用细节在拉格朗日液膜模型中描述（撞击边界时的相互作用（第500页））。

17.2.1.3 液膜分离

如果满足两个条件，液膜可以从边缘分离——首先是面之间的角度足够大，其次是液膜惯性超过一个临界值（由您定义）。如果发生分离，液膜方程中的源项用于从分离发生点上游的对应面移除质量和动量。此源项在每个液膜时间步长内累积，并在DPM迭代中使用此源项创建颗粒流。新的颗粒流仅在DPM迭代期间创建，然而由于液膜从边缘分离产生的源项在每个液膜步长中更新。

17.2.1.3.1 分离准则

根据Foucart的工作，如果超过临界角度${\theta }_{\text{critical }}$并且基于液膜的韦伯数$W{e}_f$高于最小值，液膜可以在边缘发生分离。

韦伯数定义为，

$$W{e}_f=\frac{{\rho }_{l}h{\left|{\overrightarrow{V}}_l\right|}^2}{\sigma }\text{\hspace{1em}(17.6)}$$

其中 $\sigma$ 是薄膜的表面张力。分离准则变为：

$$\{\begin{array}{c}\theta >{\theta }_{\text{critical }}\\ W{e}_f>W{e}_{\text{critical }}\end{array}\text{\hspace{1em}(17.7)}$$

图17.2：分离准则

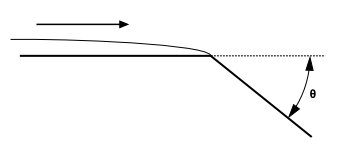
一旦发生分离，您可以根据Foucart（[188]（第1067页））、O’Rourke（[495]（第1086页））和Friedrich（[193]（第1068页））的工作，指定三种不同的模型来计算边缘处剥离粒子流的数量和直径。

17.2.1.3.1.1 Foucart分离

Foucart的边缘分离模型假设液滴直径由以下公式给出：

$$d={\left(\frac{3h^{2}l}{4\pi }\right)}^{\frac{1}{3}}\text{\hspace{1em}(17.8)}$$

其中，$l$ 是边缘的长度，$h$ 是薄膜的高度。粒子从薄膜中流出的流量 $q$ 等于薄膜沿边缘的质量通量。

$$q=V_l\cdot {\hat{n}}_{e}hl{\rho }_l\text{\hspace{1em}(17.9)}$$

其中，${\hat{n}}_e$是从边缘质心指向面中心的内向法线。根据Foucart准则从边缘分离的颗粒被赋予分离发生处薄膜边缘的速度。

17.2.1.3.1.2 O’Rourke分离

O’Rourke边缘分离模型假设液滴直径等于边缘处薄膜的高度，并且从薄膜流出的颗粒流量等于薄膜跨越边缘的质量通量。

17.2.1.3.1.3 Friedrich分离

Friedrich分离模型假设液滴直径等于边缘处薄膜的高度，但从薄膜流出的颗粒流量是根据薄膜惯性与表面张力之间的实验得出的力比来计算的。

力比由以下公式给出：

$$F_{\text{ratio }}=\frac{W{e}_f}{1+1/\sin \left(\theta \right)+F{r}_{f}W{e}_f\left(L_b/h\right)\left(1/\tan \left(\theta \right)\right)}\text{\hspace{1em}(17.10)}$$

其中，$F{r}_f=\frac{gh}{V_l^2}$，而特征破碎长度$L_b$则由下式给出：

$$L_b=0.0388h^{0.5}{\mathrm{Re}}_h^{0.6}W{e}_{rel}^{-0.5}\text{\hspace{1em}(17.11)}$$

以及相对韦伯数 ( W{e}_{rel} ) 和薄膜流动雷诺数定义如下：

$$W{e}_{rel}=\frac{{\rho }_{gas}h{\left(V_{gas}-V_l\right)}^2}{2\sigma }\text{\hspace{1em}(17.12)}$$

$${\mathrm{Re}}_h=\frac{{\rho }_f{V}_{l}h}{{\mu }_l}\text{\hspace{1em}(17.13)}$$

与O'Rourke或Foucart分离方法不同，颗粒流中的质量通量是根据实验得出的，为边缘通量的一定百分比，如方程$17.9$（第841页）所示。这个百分比被假定为力比的一个函数，具体如下：

$$\gamma =1-\exp \left(0.411544\left(\frac{1-F_{\text{ratio }}^2}{F_{\text{ratio }}}\right)\right)\text{\hspace{1em}(17.14)}$$

17.2.1.4 膜条剥离

当气相与壁面上的液膜之间存在高相对速度时，会发生膜条剥离现象。在足够高的剪切速率下，液膜表面会形成开尔文-亥姆霍兹波并逐渐增长，最终从表面剥离出液滴。在Ansys Fluent的壁面液膜模型当前实现中，这种现象的模型基于Lopez de Bertodano等人（[390]（第1079页））和Mayer（[417]（第1081页））的工作。

如Mayer所述，在剪切流中的薄液膜内，由于开尔文-亥姆霍兹型的不稳定性，会形成波长为$\lambda$的波，但这些波被液膜中的粘性力所抑制。波的增长与抑制之间的平衡提供了一个频率$\omega$的项。

注：原文中的“that is, separated flows”翻译为“即分离流”，意指在力比大于1的情况下，流动是分离的。

$$\omega =\frac{f}{{\lambda }^{1/2}}-\frac{v}{{\lambda }^2}\text{\hspace{1em}(17.15)}$$

以下文本的中文翻译：

$$f=\sqrt{\frac{\pi }{2}}\frac{\beta {\rho }_g{V}_g^2}{\sqrt{\sigma {\rho }_l}}\text{\hspace{1em}(17.16)}$$

其中 $\beta$ 是一个取值为 0.3 的保护参数，

$$v=\frac{8{\pi }^2{\mu }_l}{{\rho }_l}\text{\hspace{1em}(17.17)}$$

在公式17.16（第842页）中，$V_g$ 表示气体速度。

为了使波增长并最终从薄膜上脱离，$\omega$ 必须大于零，这意味着增长波的最小波长应为：

$$0=\frac{f}{{\lambda }^{1/2}}-\frac{v}{{\lambda }^2}\Rightarrow {\lambda }_{\min }={\left(\frac{v}{f}\right)}^{2/3}=2\pi \sqrt[3]{16}{\left(\frac{{\mu }_l\sqrt{\sigma /{\rho }_l}}{\beta {\rho }_g{V}_g^2}\right)}^{2/3}\text{\hspace{1em}(17.18)}$$

根据泰勒理论，可通过线性稳定性分析推导出频率表达式，洛佩兹·德·贝尔托达诺等人[390]（第1079页）给出了该表达式。

$$\omega =0.384\frac{{\rho }_g{V}_g^3}{\sigma }\sqrt{\frac{{\rho }_g}{{\rho }_l}}\text{\hspace{1em}(17.19)}$$

继Mayer之后，剥离液滴的平均粒径为

$$\bar{d}=F\bar{\lambda }=F\cdot \frac{9}{2}{\lambda }_{\min }\text{\hspace{1em}(17.20)}$$

在图形用户界面中，$F$（默认值为0.14）是一个数值因子，相当于直径系数。

为了在液体表面获得质量流率，假设 $\dot{m}\cong \frac{1}{2}{\rho }_{\bar{l}}\bar{\lambda }\omega$，其中 $\bar{\lambda }$ 是扰动的平均波长。Mayer 使用表达式 $\bar{\lambda }=4.5{\lambda }_{\min }$，这导致从表面剥离的液滴流率的以下表达式：

$$\dot{m}=C\frac{9}{2}{\rho }_l\omega {\lambda }_{\min }\text{\hspace{1em}(17.21)}$$

$C$（默认值为0.5）是一个数值因子，相当于图形用户界面中的质量系数。在影片计算过程中，根据上述表达式累积质量源，并在DPM迭代期间，以薄膜速度和从面计算的质量流量注入自由流。

除非液体薄膜所在的面超过了临界剪切应力（在图形用户界面中定义），否则不会从薄膜中提取质量。

17.2.1.5 次相沉积

在欧拉多相流中，收集在固体表面上的次相应与欧拉壁面薄膜模型中定义的材料相同。当次相被壁面捕获时，其质量和动量从多相流中移除，并分别作为源项添加到壁面薄膜的连续性和动量方程，即方程17.1（第838页）和方程17.2（第838页）中。

质量源项由以下公式给出：

$${\dot{m}}_s={\alpha }_d{\rho }_d{V}_{dn}A\text{\hspace{1em}(17.22)}$$

其中，${\alpha }_d$ 是第二相的体积分数，${\rho }_d$ 是第二相的密度，$V_{dn}$ 是相速度垂直于壁面的分量，而 $A$ 是壁面的表面积。

动量源由以下公式给出：

$${\dot{\overrightarrow{q}}}_s={\dot{m}}_s{\overrightarrow{V}}_d\text{\hspace{1em}(17.23)}$$

其中，${\overrightarrow{V}}_d$ 表示次相的速度矢量。

次相的收集效率计算如下：

$$\beta =\frac{{\rho }_d{V}_{dn}}{C_d{V}_d}\text{\hspace{1em}(17.24)}$$

其中，$C_d$ 和 $V_d$ 分别代表参考（远场）次相浓度和速度。

17.2.1.6 壁面液膜与混合物组分输运的耦合

欧拉壁面液膜模型也可以与混合物组分输运模型耦合，以考虑液膜材料（液体）与气体组分（蒸汽）之间的相变。相变速率采用以下模型进行建模：

• 扩散平衡模型

相变速率受以下因素控制：

$${\dot{m}}_{\text{phase }}=\frac{\left(\rho D/\delta \right)}{\rho D/\delta +C_{\text{phase }}}{C}_{\text{phase }}\left(y_{\text{sat }}-y_i\right)\left[\mathrm{kg}/{\mathrm{m}}^2-\mathrm{s}\right]\text{\hspace{1em}(17.25)}$$

其中，$\rho$ 表示气体混合物的密度，$D$ 是蒸汽物种的质量扩散率，$\delta$ 是单元中心到壁面的距离，$C_{\text{phase }}$ 是相变常数，$y_i$ 代表单元中心蒸汽物种的质量分数。饱和物种质量分数的计算如下：

$$y_{sat}=\frac{P_{sat}\left(T\right)}{P}\frac{M_i}{\bar{M}}\text{\hspace{1em}(17.26)}$$

其中，$P$ 表示气体混合物的绝对压力，$M_i$ 和 $\bar{M}$ 分别表示蒸汽组分的分子量和混合物的平均分子量。饱和压力 $P_{sat}$ 仅是温度的函数。默认情况下，假设水蒸气为蒸汽组分，其饱和压力根据 Springer 等人（[626]，第1093页）的计算方法进行计算。

$$\begin{gathered} {\log }_{10}{P}_{sat}=-2.1794+0.02953(T-273.17)-9.1837x10^{-5}(T-273.17{)}^2 \\ +1.4454x10^{-7}(T-273.17{)}^3\text{\hspace{1em}(17.27)} \end{gathered}$$

然而，在材料任务页定义蒸汽材料时，您可以通过使用用户自定义属性来替换上述默认公式。

从公式17.25（第843页）可以清楚地看出，当蒸汽质量分数超过饱和质量分数时，会发生凝结（即负的${\dot{m}}_{\text{phase }}$）；相反，当蒸汽质量分数低于饱和质量分数时，液膜会蒸发。公式17.25（第843页）中的相变常数分别对凝结和蒸发取不同的值。

$$C_{\text{phase }}=\{\begin{array}{l}{C}_{\text{con }}\\ C_{\text{vap }}h\cdot {10}^4\end{array}\text{\hspace{1em}(17.28)}$$

在以下情况下，使用薄膜高度 $h$ 来防止在没有液体存在时产生蒸汽：

• 壁面边界层模型

有关壁面边界层模型的详细信息，请参见《质量传递从薄膜》（第518页）。

• 用户定义模型

用户可以通过用户定义的轮廓UDF指定相变速率。请注意，此类UDF必须返回以 $\mathrm{kg}/\mathrm{s}$ 为单位的正值。UDF返回的速率将在代码内部转换为 $\mathrm{kg}/\mathrm{s}/{\mathrm{m}}^2$ 并带有适当的符号。

17.2.1.7 欧拉壁面薄膜与VOF多相模型的耦合

当液体薄膜积累变得显著，且薄膜厚度超过指定的最大限制时，EWF模型可能无法产生有效的计算结果。连接EWF和VOF多相模型的能力使得薄膜液体解决方案在两个模型之间进行转换，从而可以通过VOF多相模型进行积累的薄膜液体的解决方案。此外，在VOF建模中，存在流体体积靠近壁面边界变得非常小的情况。使用VOF模型解析这些小流体体积可能不切实际且成本高昂。在这种情况下，VOF到壁面薄膜的过渡允许使用EWF模型对小体积流体进行建模。

Ansys Fluent提供了耦合EWF和VOF多相模型的功能，允许针对此类情况采用混合解决方案方法。

在EWF和VOF模型过渡期间，薄膜和次相液体的质量、动量和能量项在两个模型之间进行转移。过渡可以基于以下两种过渡基础之一：

基于体积分数的过渡使用靠近薄膜壁面的计算单元中薄膜或次相液体的体积分数。

基于高度分数的过渡则使用薄膜或等效薄膜半高度与单元中心到薄膜壁面距离的比值。

对于这两种过渡基础，都会根据指定的过渡准则计算出一个加权的薄膜高度阈值，并用于确定过渡的开始。

17.2.2 部分润湿效应

薄膜液体部分润湿的效果描述了壁面上如细流、干燥斑块和薄膜破裂等行为，并采用Meredith [435]（第1082页）描述的部分润湿模型进行建模。

由于薄膜表面张力 ${\overrightarrow{\tau }}_{{\theta }_w}$ 在公式17.2（第838页）中表示为：

$${\overrightarrow{\tau }}_{{\theta }_w}=\beta \sigma \left(1-\cos {\theta }_w\right){\nabla }_{s}w\text{\hspace{1em}(17.29)}$$

其中，$\sigma$ 表示薄膜表面张力，$\beta$ 是一个经验参数，用于解释模型与观测到的薄膜行为之间的差异，而 $w$ 代表薄膜湿润面积的分数。

薄膜接触角 ${\theta }_w$ 从以平均接触角 ${\theta }_m$ 及其标准差 $\alpha {\theta }_m$（其中 $\alpha$ 是一个百分比分数因子）为特征的高斯分布中随机抽取。接触角也可以通过用户自定义函数（UDFs）来指定。

薄膜湿润面积的分数定义如下：

$$w=\{\begin{array}{ll}1,& h>h_c\\ 0,& h\le h_c\end{array}\text{\hspace{1em}(17.30)}$$

其中，$h_c$ 是临界膜厚度。如果液膜厚度超过临界值 $h_c$，则认为壁面是湿润的。如果膜厚度低于此值，则认为壁面是干燥的。在 Ansys Fluent 的欧拉壁膜（EWF）模型中，$h_c$ 取值为 1e-10米。

17.2.3 边界条件

方程 17.1（第 838 页）和方程 17.2（第 838 页）的边界条件，即膜质量和动量方程，仅在启用了膜建模的壁面上指定。有两种类型的条件：一种是固定质量和动量通量，另一种是规定的初始膜高度和速度。当指定通量时，它们作为源项添加到方程中。当指定初始膜高度和速度时，这些值仅在第一个膜时间步长上强制执行。

17.2.4 在不求解动量方程的情况下获得膜速度

方程 17.2（第 838 页）用于通过动量守恒获得膜平均速度。然而，可以不通过求解方程 17.2（第 838 页）来估计膜速度。在这种情况下，假定膜速度由外部流动引起的剪切力和重力驱动。

17.2.4.1 剪切力驱动的膜速度

如图 17.3 所示：剪切力驱动的膜速度（第 846 页），假设膜速度从壁面到气膜界面线性变化。

图 17.3：剪切力驱动的膜速度

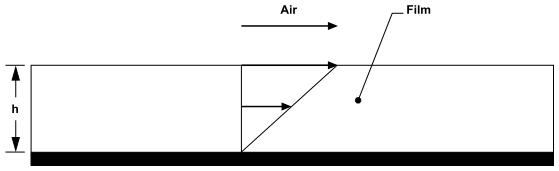
通过在膜-空气界面处等同来自空气侧和膜侧的两个剪切力，我们得到，

$${\overrightarrow{\tau }}_{air}={\mu }_l\frac{\partial \overrightarrow{V}}{\partial n}={\mu }_l\frac{{\overrightarrow{V}}_s}{h}\text{\hspace{1em}(17.31)}$$

其中，${\overrightarrow{V}}_s$ 表示表面速度。因此，薄膜平均速度为：

$${\overrightarrow{V}}_l=\frac{{\overrightarrow{\tau }}_{air}h}{2{\mu }_l}\text{\hspace{1em}(17.32)}$$

17.2.4.2 重力驱动薄膜速度

假设薄膜运动完全由重力与壁面剪切力的平衡所控制，并且薄膜速度具有在空气-薄膜界面处梯度为零的抛物线轮廓，如图17.4所示：重力驱动薄膜速度（第847页）。

图17.4：重力驱动薄膜速度

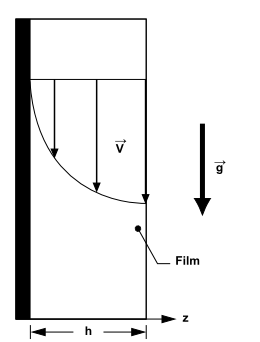
假设在壁面处无滑移，抛物线薄膜速度变为 $\overrightarrow{V}\left(z\right)=\overrightarrow{a}{z}^2+\overrightarrow{b}z$。

通过平衡薄膜的重量和壁面剪切力，我们有，

$${\rho }_{l}Ah\overrightarrow{g}={A{\mu }_l\frac{\partial \overrightarrow{V}}{\partial z}|}_{z=0}={\mu }_l{\left(2\overrightarrow{a}z+\overrightarrow{b}\right)}_{z=0}\text{\hspace{1em}(17.33)}$$

因此，

$$\overrightarrow{b}=\frac{{\rho }_{l}h}{{\mu }_l}\overrightarrow{g}\text{\hspace{1em}(17.34)}$$

在空气-薄膜界面应用零梯度假设，我们有：

$$\overrightarrow{a}=-\frac{\overrightarrow{b}}{2h}=-\frac{{\rho }_l}{2{\mu }_l}\overrightarrow{g}\text{\hspace{1em}(17.35)}$$

因此，重力诱导的薄膜速度为：

$$\overrightarrow{V}\left(z\right)=\frac{{\rho }_{l}h}{{\mu }_l}z\left(1-\frac{z}{2h}\right)\overrightarrow{g}\text{\hspace{1em}(17.36)}$$

影片平均速度为，

$${\overrightarrow{V}}_l=\frac{{\rho }_l{h}^2}{3{\mu }_l}\overrightarrow{g}\text{\hspace{1em}(17.37)}$$