Ansys Fluent 提供了以下几种液滴破碎模型：

• Taylor 类比破碎（TAB）模型

TAB 模型推荐用于低韦伯数喷射，非常适合低速喷雾进入标准大气环境。

• 波模型

波模型更适用于韦伯数大于 100 的情况。

• KHRT 模型

KHRT 模型在上述应用领域之间提供了一个过渡，它考虑了气动破碎与液滴加速引起的稳定性竞争效应，并结合 Levich 模型来计算液核长度。

• 随机次级液滴（SSD）模型

SSD 模型将高韦伯数下的破碎视为离散随机事件，导致在一个范围内分布不同直径尺度的液滴。

• Madabhushi 破碎模型

Madabhushi 破碎模型适用于亚音速横流中液体射流的数值模拟。

• Schmehl 破碎模型

Schmehl 破碎模型采用先进的次级破碎模拟方法，包括袋状、多模式和剪切机制，以提高对喷雾物理特性的描述。

波模型和 KHRT 模型在高速燃油喷射应用中较为流行。模型的选择取决于液滴破碎中动量和表面张力的相对重要性，这由韦伯数描述，其定义见公式 12.406（第 557 页）。

每个模型的详细信息在以下章节中提供：

12.13.1. Taylor 类比破碎（TAB）模型

12.13.2. 波破碎模型

12.13.3. KHRT 破碎模型

12.13.4. 随机次级液滴（SSD）模型

12.13.5. Madabhushi 破碎模型

12.13.6. Schmehl 破碎模型

12.13.1 Taylor 类比破碎（TAB）模型

12.13.1.1 介绍

Taylor 类比破碎（TAB）模型是一种经典的计算液滴破碎的方法，适用于多种工程喷雾。该方法基于 Taylor 的类比 [647]（第 1094 页）。

在振荡和变形的液滴与弹簧质量系统之间。表12.9：弹簧质量系统与变形液滴的比较（第556页）展示了类似的组成部分。

表12.9：弹簧质量系统与变形液滴的比较

由此产生的TAB模型方程组，控制着液滴的振荡和变形，可以求解以确定任意时刻液滴的振荡和变形。如下面详细描述的，当液滴振荡增长到临界值时，“母”液滴将破碎成多个较小的“子”液滴。随着液滴从球形变形，阻力系数会发生变化。Ansys Fluent中提供了包含变形液滴效应的阻力模型。详情请参见动态阻力模型理论（第459页）。

12.13.1.2 使用与限制

TAB模型最适合于低韦伯数喷雾。极高韦伯数的喷雾会导致液滴破碎，这不能很好地用弹簧质量类比来描述。

12.13.1.3 液滴变形

控制阻尼强迫振荡器的方程是[494]

$$F-kx-d\frac{dx}{dt}=m\frac{d^{2}x}{d{t}^2}$$

其中，$x$ 表示液滴赤道相对于其球形（未受扰动）位置的位移。该方程的系数取自泰勒的类比分析：

$$\frac{F}{m}=C_F\frac{{\rho }_g{u}^2}{{\rho }_{l}r}$$

（12.400）

$$\frac{k}{m}=C_k\frac{\sigma }{{\rho }_l{r}^3}$$

(12.401)

$$\frac{d}{m}=C_d\frac{{\mu }_l}{{\rho }_l{r}^2}$$

(12.402)

其中，${\rho }_l$ 和 ${\rho }_g$ 分别表示离散相和连续相的密度，$u$ 是液滴的相对速度，$r$ 是未受扰动的液滴半径，$\sigma$ 是液滴的表面张力，${\mu }_l$ 是液滴的粘度。无量纲常数 $C_F$、$C_k$ 和 $C_d$ 将在后面定义。

假设当变形增长到液滴半径的临界比值时，液滴会发生破碎。这一破碎条件表述如下：

$$x>C_{b}r$$

公式 (12.403) 中，$C_b$ 是一个常数，等于 0.5。如果假设破碎发生时变形等于液滴半径的一半，即南北极的振荡以该幅度在液滴中心相遇。这隐含地假定了液滴仅经历一个（基本）振荡模式。通过设定 $y=x/\left(C_{b}r\right)$ 并代入公式 (12.400) 至公式 (12.402) 中的关系，公式 (12.399) 被无量纲化。

$$\frac{d^{2}y}{d{t}^2}=\frac{C_F}{C_b}\frac{{\rho }_g}{{\rho }_l}\frac{u^2}{r^2}-\frac{C_k\sigma }{{\rho }_l{r}^3}y-\frac{C_d{\mu }_l}{{\rho }_l{r}^2}\frac{dy}{dt}$$

(12.404)

其中，破碎现象在 $y>1$ 时发生。对于欠阻尼的液滴，如果假设相对速度恒定，可以从方程 12.404（第 557 页）轻松确定控制 $y$ 的方程：

$$y\left(t\right)=W{e}_c+e^{-\left(t/t_d\right)}\left[\left(y_0-W{e}_c\right)\cos \left(\omega t\right)+\frac{1}{\omega }\left(\frac{d{y}_0}{dt}+\frac{y_0-W{e}_c}{t_d}\right)\sin \left(\omega t\right)\right]$$

其中

$$We=\frac{{\rho }_g{u}^{2}r}{\sigma }$$

(12.406)

$$W{e}_c=\frac{C_F}{C_k{C}_b}We$$

（12.407）

$$y_0=y\left(0\right)$$

(12.408)

$$\frac{d{y}_0}{dt}=\frac{dy}{dt}\left(0\right)$$

(12.409)

$$\frac{1}{t_d}=\frac{C_d}{2}\frac{{\mu }_l}{{\rho }_l{r}^2}$$

(12.410)

$${\omega }^2=C_k\frac{\sigma }{{\rho }_l{r}^3}-\frac{1}{t_d^2}$$

在公式12.405（第557页）中，$u$表示液滴与气相之间的相对速度，而$We$则是液滴韦伯数，这是一个无量纲参数，定义为气动力与表面张力之比。液滴的振动频率由$\omega$表示。基于刘等人[385]（第1079页）的研究，$y_0$的默认值为0。这些常数的选择是为了与实验和理论[331]（第1076页）相匹配：

$$C_k=8$$

(12.412)

$$C_d=5$$

$$C_F=\frac{1}{3}$$

如果针对所有液滴求解方程 12.405（第 557 页），那些满足 $y>1$ 的液滴被认为会发生破碎。此时需要确定新生成子液滴的大小和速度。

12.13.1.4 子液滴的大小

子液滴的大小是通过将母液滴的能量等同于子液滴合并后的能量来确定的。母液滴的能量为 [494]（第 1085 页）。

$$E_{\text{parent }}=4\pi r^2\sigma +K\frac{\pi }{5}{\rho }_l{r}^5\left[{\left(\frac{dy}{dt}\right)}^2+{\omega }^2{y}^2\right]$$

其中，$K$ 是畸变和振荡中的总能量与基模态能量之比，其数量级为 $\left(\frac{10}{3}\right)$。假设子液滴未发生畸变且无振荡。因此，可以证明子液滴的能量为

$$E_{\text{child }}=4\pi r^2\sigma \frac{r}{r_{32}}+\frac{\pi }{6}{\rho }_l{r}^5{\left(\frac{dy}{dt}\right)}^2$$

其中，$r_{32}$ 表示液滴尺寸分布的索特平均半径。可以通过将母液滴和子液滴的能量相等（即，方程 12.413（第 557 页）和方程 12.414（第 558 页）），设定 $y=1$，以及 ${\omega }^2=8\sigma /{\rho }_l{r}^3$ 来求得 $r_{32}$。

$$r_{32}=\frac{r}{1+\frac{8K{y}^2}{20}+\frac{{\rho }_l{r}^3{\left(dy/dt\right)}^2}{\sigma }\left(\frac{6K-5}{120}\right)}$$

一旦确定了子液滴的大小，通过质量守恒可以轻松计算出子液滴的数量。

12.13.1.5 子液滴的速度

TAB模型允许在子液滴上施加一个垂直于母液滴速度的分量。当破裂发生时，母液滴的赤道以速度 $dx/dt=C_{b}r\left(dy/dt\right)$ 移动。因此，子液滴将具有垂直于母液滴速度的速度，由以下公式给出：

$$v_{\text{normal }}=C_v{C}_{b}r\frac{dy}{dt}$$

(12.416)

其中，$C_v$ 是一个数量级为 (1) 的常数。

12.13.1.6 液滴破碎

为了模拟液滴破碎，TAB 模型首先在每个时间步 $n$ 确定每个液滴的无阻尼振荡幅度 $\left(t_d\approx \infty \right)$，具体如下：

$$A=\sqrt{{\left(y^n-W{e}_c\right)}^2+{\left(\frac{{\left(dy/dt\right)}^n}{\omega }\right)}^2}$$

根据公式12.417（第558页），只有满足以下条件时，破碎才可能发生：

$W{e}_c+A>1$

（12.418）

这是极限情况，因为阻尼只会降低破碎的可能性。如果一个液滴不满足上述标准，则不会发生破碎。此时所需的唯一额外计算，是使用O'Rourke和Amsden [494]（第1085页）所做工作的离散形式来更新$y$，这基于公式12.405（第557页）及其导数：

$$y^{n+1}=W{e}_c+e^{-\left(\Delta t/t_d\right)}\left\{\left(y^n-W{e}_c\right)\cos \left(\omega t\right)+\frac{1}{\omega }\left[{\left(\frac{dy}{dt}\right)}^n+\frac{y^n-W{e}_c}{t_d}\right]\sin \left(\omega t\right)\right\}$$

(12.419)

$${\left(\frac{dy}{dt}\right)}^{n+1}=\frac{W{e}_c-y^{n+1}}{t_d}+\omega e^{-\left(\Delta t/t_d\right)}\left\{\frac{1}{\omega }\left[{\left(\frac{dy}{dt}\right)}^n+\frac{y^n-W{e}_c}{t_d}\right]\cos \left(\omega \Delta t\right)-\left(y^n-W{e}_c\right)\sin \left(\omega \Delta t\right)\right\}$$

(12.420)

在这些表达式中，所有常数都被假定在整个时间步长内保持恒定。

如果满足公式12.418（第558页）的条件，则可能发生破碎。必须确定破碎时间 ( t_{bu} )，以查看破碎是否在时间步长 ( \Delta t ) 内发生。 ( t_{bu} ) 的值设定为振荡增长到足够大以至于液滴变形 ( y ) 达到单位值所需的时间。在假设液滴振荡在其第一个周期内无阻尼的情况下，确定破碎时间。因此，破碎时间是大于 ( t^n ) 的无阻尼版本公式12.405（第557页）的最小根：

$$W{e}_c+A\cos \left[\omega \left(t-t^n\right)+\phi \right]=1$$

其中

$$\cos \phi =\frac{y^n-W{e}_c}{A}$$

（12.422）

以及

$$\sin \phi =-\frac{{\left(dy/dt\right)}^n}{A\omega }$$

(12.423)

若 $t_{bu}>t^{n+1}$，则当前时间步内不会发生破碎，$y$ 及 $(dy/dt)$ 将依据公式 12.419（第 558 页）和公式 12.420（第 558 页）进行更新。随后，破碎计算将继续处理下一个液滴。相反，如果 $t^n<t_{bu}<t^{n+1}$，则将发生破碎，子液滴的半径由公式 12.415（第 558 页）确定。子液滴的数量 $N$ 则通过质量守恒来确定：

$$N^{n+1}=N^n{\left(\frac{r^n}{r^{n+1}}\right)}^3$$

假设子液滴既不变形也不振荡；即 $y=\left(dy/dt\right)=0$。子液滴由从原始液滴中创建的多个子包裹体表示。这些子包裹体均匀分布在父液滴赤道上的一个平面内，该平面垂直于父液滴的相对速度矢量。每个子包裹体的直径根据基于索特平均半径（公式12.415（第558页））和3.5的扩展参数的Rosin Rammler分布进行采样。

在子液滴上施加一个垂直于相对速度矢量的速度分量，其大小由公式12.416（第558页）计算。它在地平线上分解为径向向外的分量。

重要提示：大量的子包裹体确保了粒径和源项的平滑分布，这在模拟蒸发喷雾等情况时是必需的。

12.13.2 波浪破碎模型

12.13.2.1 介绍

对于高韦伯数流动，Reitz [547]（第1088页）的波浪破碎模型是TAB模型的替代方案，该模型考虑了气液相之间的相对速度引起的液滴破碎。该模型假设破碎时间和产生的液滴大小与从下面描述的射流稳定性分析中得出的最快增长的Kelvin-Helmholtz不稳定性有关。这种不稳定性的波长和增长率用于预测新形成液滴的细节。

12.13.2.2 使用和限制

波浪模型适用于高速注射，其中据信Kelvin-Helmholtz不稳定性主导液滴破碎（$We>100$）。由于这种破碎模型可能会增加计算包裹体的数量，您可能希望最初注射适量的液滴。

12.13.2.3 射流稳定性分析

Reitz和Bracco[549]（第1089页）详细描述的射流稳定性分析在此简要介绍。该分析考虑了一个圆柱形、粘性液体射流，其半径为$a$，从圆形喷嘴以速度$v$喷出，进入密度为${\rho }_2$的静止、不可压缩、无粘性气体中。液体具有密度${\rho }_1$和粘度${\mu }_1$，并采用随射流移动的圆柱极坐标系。分析中考虑了任意微小的轴对称表面位移，形式为...

$$\eta ={\eta }_0{e}^{ikz+\omega t}$$

(12.425)

施加于初始稳态运动之上，因此希望找到色散关系 $\omega =\omega \left(k\right)$，该关系将增长率 $\omega$ 的实部与其波数 $k=2\pi /\lambda$ 联系起来。

为了确定色散关系，假设波解的形式，求解液体水动力学的线性化方程。

$${\phi }_1=C_1{I}_0\left(kr\right)e^{ikz+\omega t}$$

（12.426）

$${\psi }_1=C_2{I}_1\left(Lr\right)e^{ikz+\omega t}$$

其中，${\phi }_1$ 和 ${\psi }_1$ 分别代表速度势和流函数，$C_1$ 和 $C_2$ 是积分常数，$I_0$ 和 $I_1$ 是第一类修正贝塞尔函数，$L^2=k^2+\omega /v_1$，而 $v_1$ 则是液体运动粘度 [547]（第1088页）。液体压力可由液体方程中的无粘性部分求得。此外，无粘性气体方程亦可求解，以获得在 $r=a$ 处的气体脉动压力：

$$-p_{21}=-{\rho }_2{\left(U-i\omega k\right)}^{2}k\eta \frac{K_0\left(ka\right)}{K_1\left(ka\right)}$$

其中，$K_0$ 和 $K_1$ 是第二类修正贝塞尔函数，$u$ 是液体与气体之间的相对速度。线性化的边界条件为

$${\mathrm{v}}_1=\frac{\partial \eta }{\partial t}$$

(12.429)

$$\frac{\partial u_1}{\partial r}=-\frac{\partial v_1}{\partial z}$$

（12.430）

以及

$$-p_1+2{\mu }_1-\frac{\sigma }{a^2}\left(\eta +a^2\frac{{\partial }^2\eta }{\partial z^2}\right)+p_2=0$$

这些方程分别是液体运动学自由表面条件的数学表述、剪切应力的连续性以及法向应力的连续性。注意，$u_1$ 是轴向扰动液体速度，$v_1$ 是径向扰动液体速度，$\sigma$ 是表面张力。同时请注意，方程 12.430（第 560 页）是在假设 $v_2=0$ 的条件下得到的。

如 Reitz [547]（第 1088 页）所述，方程 12.429（第 560 页）和方程 12.430（第 560 页）可用于消除方程 12.426（第 560 页）和方程 12.427（第 560 页）中的积分常数 $C_1$ 和 $C_2$。因此，当将压力和速度解代入方程 12.431（第 560 页）时，便可得到所需的色散关系：

$${\omega }^2+2v_1{k}^2\omega \left[\frac{I_1^{\prime }\left(ka\right)}{I_0\left(ka\right)}-\frac{2kL}{k^2+L^2}\frac{I_1\left(ka\right)}{I_0\left(ka\right)}\frac{I_1^{\prime }\left(La\right)}{I_1\left(La\right)}\right]=\frac{\sigma k}{{\rho }_1{a}^2}\left(1-k^2{a}^2\right)\left(\frac{L^2-a^2}{L^2+a^2}\right)\frac{I_1\left(ka\right)}{I_0\left(ka\right)}$$

（12.432）

$$+\frac{{\rho }_2}{{\rho }_1}{\left(U-i\frac{\omega }{k}\right)}^2\left(\frac{L^2-a^2}{L^2+a^2}\right)\frac{I_1\left(ka\right)}{I_0\left(ka\right)}\frac{K_0\left(ka\right)}{K_1\left(ka\right)}$$

如Reitz [547]（第1088页）所示，方程12.432（第561页）预测在给定流动条件下存在一个最大增长率（或最不稳定波）。针对最大增长率$\Omega$及其对应波长$\Lambda$，Reitz [547]（第1088页）给出了数值解拟合曲线：

$$\frac{\Lambda }{a}=9.02\frac{\left(1+0.450h^{0.5}\right)\left(1+0.4{\mathrm{Ta}}^{0.7}\right)}{{\left(1+0.87W{e}_2^{1.67}\right)}^{0.6}}$$

（12.433）

$$\Omega \sqrt{\frac{{\rho }_{{}_1}{a}^3}{\sigma }}=\frac{0.34+0.38W{e}_2^{1.5}}{\left(1+Oh\right)\left(1+1.4T{a}^{0.6}\right)}$$

其中 $Oh=\sqrt{W{e}_1}/R{e}_1$ 是 Ohnesorge 数，$Ta=Oh\sqrt{W{e}_2}$ 是 Taylor 数。此外，$W{e}_1={\rho }_1{U}^{2}a/\sigma$ 和 $W{e}_2={\rho }_2{U}^{2}a/\sigma$ 分别是液体和气体的韦伯数，$R{e}_1=Ua/v_1$ 是雷诺数。

12.13.2.4 液滴破碎

在波模型中，液滴包的破碎是通过假设新生成的液滴半径与母液滴上增长最快的非稳定表面波的波长成正比来计算的。换句话说，

$$r=B_0\Lambda$$

其中，$B_0$ 是一个根据Reitz [547]（第1088页）的工作设定为0.61的模型常数。此外，母包中液滴半径的变化率由以下公式给出：

$$\frac{da}{dt}=-\frac{\left(a-r\right)}{\tau },r\le a$$

其中，破裂时间 $\tau$ 由以下公式给出：

$$\tau =\frac{3.726B_{1}a}{\Lambda \Omega }$$

并且，$\Lambda$ 和 $\Omega$ 分别从方程 12.433（第 561 页）和方程 12.434（第 561 页）获得。破碎时间常数 $B_1$ 设置为 1.73，这是根据 Liu 等人 [385]（第 1079 页）的建议。$B_1$ 的值可以在 1 到 60 之间变化，具体取决于喷嘴的特性。

在波模型中，质量从母滴以方程 $12.437\left(\mathrm{p}.561\right)$ 给出的速率累积，直到分离的质量等于初始包裹质量的 $5\%$。此时，创建一个新的包裹。子颗粒的直径由方程 12.435（第 561 页）给出。新包裹被赋予与母包裹相同的属性（即温度、材料、位置等），除了半径和速度。新包裹被赋予一个在垂直于母包裹方向矢量的平面内随机选择的速度分量，并且调整母包裹的动量以保持动量守恒。新包裹的速度大小与母包裹相同。

您还必须指定决定气相如何与液滴相互作用的模型常数。例如，破碎时间常数 B1 是乘以时间尺度的常数，该时间尺度决定了包裹失去质量的速度。因此，较大的数值意味着颗粒失去一定质量所需的时间更长。在气相相互作用的背景下，B1 的较大数值意味着与子网格的相互作用较弱。B0 是液滴尺寸的常数，通常取为 0.61。

在低气体韦伯数（瑞利机制）下，圆柱形液流的初始断裂过程中，方程12.435（第561页）预测的液滴直径可能大于初始（液流）直径。在这种情况下，液滴的大小是根据增长最快的波长计算的，该波长决定了初始液滴的间距，并考虑了质量守恒的因素。如《Fluent用户指南》中的“断裂”部分所述，您可以抑制对瑞利机制的这种考虑。

12.13.3 KHRT断裂模型

12.13.3.1 介绍

Ansys Fluent提供了一种替代的液滴断裂模型，称为KHRT（[54]（第1060页），[509]（第1086页）），该模型结合了由气动力驱动的开尔文-亥姆霍兹波效应和由于喷射到自由流条件下的脱落液滴加速引起的瑞利-泰勒不稳定性。这两种机制都是通过追踪液滴表面的波增长来模拟液滴断裂，断裂是由于基于局部条件的最快增长不稳定性导致的。为了模拟近喷嘴区域的液核，应用了仅允许开尔文-亥姆霍兹波增长引起的断裂的列维奇核长度。

12.13.3.2 使用与限制

KHRT模型是为模拟高韦伯数喷雾而开发的，不应应用于低压喷雾。

12.13.3.3 液核长度

KHRT模型假设在近喷嘴区域存在一个液核。子液滴从该液核脱落，并在喷射到自由流中时受到突然加速，此时瑞利-泰勒不稳定性成为主导效应。液核的长度根据列维奇理论[359]（第1078页）获得：

$$L=C_L{d}_0\sqrt{\frac{{\rho }_l}{{\rho }_g}}$$

其中，$C_L$ 是 Levich 常数，$d_0$ 是参考喷嘴直径。在 Ansys Fluent 中，对于雾化喷射必须指定参考直径，然而锥形和实心锥形喷射则假设参考直径为液滴直径和锥体内径中的较小值。表面喷射使用指定的表面面积来计算等效水力直径，并将其作为 $d_0$。当为非雾化喷射指定 Rosin-Rammler 分布时，Rosin-Rammler 的最大直径成为参考直径。

液核通过“团块”[54]（第 1060 页）近似表示，如图 12.23 所示：液核近似（第 563 页）。

图 12.23：液核近似

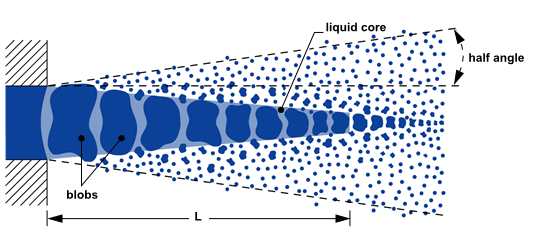
这些“团块”以喷射中指定的直径引入计算域。通常，通过考虑收缩系数来使用有效液滴直径效果最佳，该收缩系数可以计算得出。

$$D_e=\sqrt{C_a}\cdot d_0$$

其中，$C_a$ 表示收缩系数。

如《Fluent用户指南》中所述，通过将Levich常数 $C_L$ 设置为零，可以完全禁用液核近似。

12.13.3.4 Rayleigh-Taylor破碎

与Kelvin-Helmholtz模型类似，Rayleigh-Taylor（RT）模型基于液滴表面的波动不稳定性。最快增长波的频率是通过计算得出的。

$${\Omega }_{RT}=\sqrt{\frac{2{\left(-g_t\left({\rho }_p-{\rho }_g\right)\right)}^{3/2}}{3\sqrt{3\sigma }\left({\rho }_p+{\rho }_g\right)}}$$

其中，$g_t$ 表示液滴在液滴行进方向上的加速度。相应的波数则由以下公式给出：

$$K_{RT}=\sqrt{\frac{-g_t\left({\rho }_p-{\rho }_g\right)}{3\sigma }}$$

(12.441)

当RT波增长的时间超过其破裂时间${\tau }_{RT}$时，破裂现象便会出现。这里，${\tau }_{RT}$被定义为

$${\tau }_{RT}=\frac{C_{\tau }}{{\Omega }_{RT}}$$

(12.442)

此处，$C_{\tau }$ 是瑞利-泰勒破碎时间常数，其默认值为 0.5。

当预测的波长 $2\pi C_{RT}/K_{RT}$（对应于最快的波增长速率）小于局部液滴直径时，会追踪波的增长。较小子液滴的半径通过以下方式计算：

$$r_c=\frac{\pi C_{RT}}{K_{RT}}$$

其中，$C_{RT}$ 是破碎半径常数，默认值为0.1。

12.13.3.5 液核内的液滴破碎

在液核内部仅考虑气动力破碎。它是基于上一节中描述的波动破碎模型计算的。

12.13.3.6 液核外的液滴破碎

在液核外部，同时计算 KH 和 RT 效应，并且两者都被考虑用于破碎。通常情况下，当液滴加速度较高时，RT 不稳定性增长更快，这种效应在高韦伯数喷雾中占主导地位。在这两种情况下，仅当累积的脱落液滴质量超过初始液滴质量的 $5\%$ 时，才会生成新的液滴团。

12.13.4 随机次级液滴（SSD）模型

在波动和 TAB 喷雾模型中，液滴破碎是使用单一直径尺度确定的。SSD 模型 [24]（第 1058 页）将破碎视为离散随机事件，导致直径尺度分布范围。使用 SSD 模型，破碎概率与母液滴大小无关，次级液滴大小从福克-普朗克方程的概率分布的解析解中采样。此外，尺寸分布的参数基于局部条件。

注入到域中的液滴团的初始直径在 DPM 注入对话框中设置。破碎模型预测破碎发生的时间以及新液滴的数量和属性。大于临界半径的液滴会受到破碎的影响。

$$r_c=\frac{W{e}_{cr}{\sigma }_l}{{\rho }_g{u}_{rel}^2}$$

(12.444)

其中，$W{e}_{cr}$ 是临界韦伯数，需要您指定。临界韦伯数的默认值为 6。

破碎时间定义为

$$t_{bu}=B\sqrt{\frac{{\rho }_l}{{\rho }_g}}\frac{r}{\left|u_{rel}\right|}$$

(12.445)

其中，$B$ 是用户指定的破碎常数，默认值为 1.73。

半径大于临界半径（由临界韦伯数导出）的液滴，其破碎时间会增加。当包裹上的破碎时间大于临界破碎时间（根据单元格和包裹上的局部条件计算得出）时，破碎发生。

当一个包裹达到破碎点时，它会被销毁，并创建新的包裹。这些子包裹的直径通过对数直径 $x=\ln \left(r\right)$ 上的分布函数进行采样获得。

$$T\left(x\right)=\frac{1}{\sqrt{2\pi ⟨{\xi }^2⟩}}\exp \left[\frac{-{\left(x-x_0-⟨\xi ⟩\right)}^2}{2⟨{\xi }^2⟩}\right]$$

其中，$⟨\xi ⟩$ 和 $⟨{\xi }^2⟩$ 是模型的参数。

参数 $⟨\xi ⟩$ 具有负的无量纲值，需要由您设定：$\exp \left(⟨\xi ⟩\right)$ 是子颗粒相对于原始颗粒大小的典型因子。

参数 $⟨{\xi }^2⟩$ 定义了子颗粒分布的对数方差。

它具有正的无量纲值，应显著小于 $⟨\xi {⟩}^2$（以避免子颗粒大于原始颗粒）。它是从 $⟨{\xi }^2⟩=-0.1\ln \left(\frac{W{e}_{cr}}{We}\right)$ 计算得出的。

当发生破碎时，会创建足够多的颗粒，使得每个颗粒所代表的液滴数量大约等于您设定的目标数量（NP）。颗粒的直径从分布中随机抽样，并暂时赋予目标NP。这一过程持续到父颗粒的质量被耗尽。然后，对所有新颗粒中的液滴数量应用一个缩放因子，以保持父颗粒的质量守恒。

这种方法提高了统计性能，并让您在模拟过程中控制误差。较小的NP意味着更多的颗粒但统计误差较低。然而，在一次破碎事件中可以创建的颗粒数量是有限制的；此限制的默认值为50。因此，每个颗粒中的液滴数量有时会显著偏离目标NP。

12.13.5 Madabhushi 破碎模型

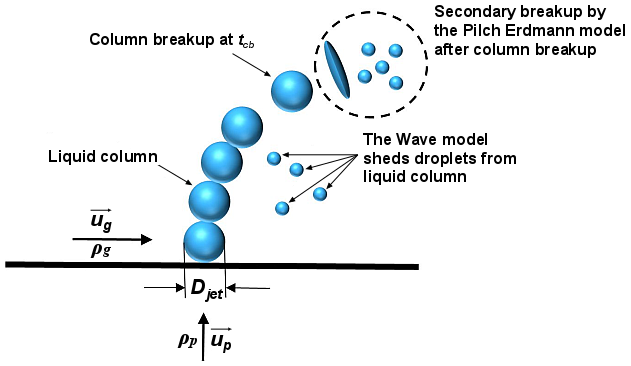
在Madabhushi框架[407]（第1080页）中，初级破碎效果通过Wave模型模拟，而次级破碎效果则采用Pilch和Erdman[517]（第1087页）提出的模型进行模拟。图12.24：Madabhushi破碎模型（第566页）展示了Madabhushi破碎模型中考虑的颗粒破碎机制。

图12.24：Madabhushi破碎模型

液滴通过出口直径为$D_{jet}$的孔口注入。在初级破碎阶段，射流被表示为直径相等的球形液滴柱，其直径$D_0=D_{jet}$。初始液滴速度$u_p$根据入口射流速度和液体密度（或流量）计算得出。在此阶段，根据标准WAVE破碎模型生成子液滴。随后，对于这些子液滴的破碎（由于湍流、毛细管和气动力引起的次级破碎），则采用Pilch和Erdman模型[517]（第1087页）进行建模。

液滴保持在液柱中，直到所谓的柱破碎时间$t_{cb}$达到为止。

$$t_{cb}=C_0\frac{D_0}{u_g}\sqrt{\frac{{\rho }_l}{{\rho }_g}},C_0=3.44$$

其中，$u_g$ 是横流气体速度，${\rho }_l$ 是液体密度，${\rho }_g$ 是气体密度。$C_0$ 是柱状破碎时间常数。其值在不同文献中有所不同。Ansys Fluent 采用了 Madabhushi [407]（第 1080 页）提出的值，即 $C_0=3.44$。在此阶段，阻力保持不变，$C_D=1.48$。

一旦液滴寿命超过柱状破碎时间 $t_{cb}$，它将根据 Pilch 和 Erdman 的模型 [517]（第 1087 页）经历二次破碎。在该模型中，液滴在变形周期 $t_{\text{def }}$ 内从球形变形为圆盘形：

$$t_{\text{def }}=1.6t^{\ast }$$

其中，$t^{\ast }$ 是给定的破碎特征时间尺度，具体为：

$$t^{\ast }=\frac{D_{\text{parent }}}{u_{\text{rel }}}\sqrt{\frac{{\rho }_l}{{\rho }_g}}$$

(12.449)

此处，$u_{\text{rel }}$ 表示液滴与气体之间的相对速度，而 $D_{\text{parent }}$ 则是在柱状破碎时刻 $t_{cb}$ 处的局部液滴直径。

在变形期间，液滴的阻力变化遵循以下表达式：

$$C_D=C_D^{\text{sphere }}\left(1-\frac{t}{t_{\text{def }}}\right)+C_D^{\text{disc }}\frac{t}{t_{\text{def }}},t<t_{\text{def }}$$

(12.450)

其中，圆盘的阻力系数为 $C_D^{disc}=1.2$。

阻力参考面积根据以下表达式变化：

$$D_{\text{ref }}=\{\begin{array}{cc}\left(1+0.19\sqrt{We}\frac{t}{t_{\text{def }}}\right)D_{\text{parent }}& t<t_{\text{def }},We<100\\ \left(1+1.9\frac{t}{t_{\text{def }}}\right)D_{\text{parent }}& t<t_{\text{def }},We\ge 100\end{array}$$

作用在液滴上的阻力变化如下：

$$F_D=\frac{1}{2}{\rho }_g{C}_D{A}_P^{\ast }\cdot \left|{\overrightarrow{u}}_g-{\overrightarrow{u}}_p\right|\cdot \left({\overrightarrow{u}}_g-{\overrightarrow{u}}_p\right)$$

其中，$C_D$ 是阻力系数，而 $A_P^{\ast }$ 是通过以下公式计算的横截面面积：

$$A_P^{\ast }=\frac{\pi }{4}{D}_{\text{ref }}^2=\frac{D_{\text{ref }}^2}{D_{\text{parent }}^2}\frac{\pi }{4}{D}_{\text{parent }}^2={\left(\frac{D_{\text{ref }}}{D_{\text{parent }}}\right)}^2{A}_P^{\text{parent }}$$

一旦达到形变时间 $t_{def}$，液滴将保持形变状态，阻力保持恒定：

$$C_D=C_D^{\text{disc }},D_{\text{ref }}=\{\begin{array}{ll}\left(1+0.19\sqrt{We}\right)D_{\text{parent }}& We<100\\ 2.9D_{\text{parent }}& We\ge 100\end{array}$$

直到液滴分裂成五个更小的子液滴包。

总分裂时间 $t_b$ 取决于局部韦伯数，并由以下相关性确定：

$$\frac{t_b}{t^{\ast }}=\{\begin{array}{ll}6{\left(We-12\right)}^{-0.25},& 12<We<18\\ 2.45{\left(We-12\right)}^{0.25},& 18<We<45\\ 14.1{\left(We-12\right)}^{-0.25},& 45<We<351\\ 0.776{\left(We-12\right)}^{0.25},& 351<We<2670\\ 5.5,& 2670<We\end{array}$$

(12.455)

由于边缘扩张，每个子液滴的速度 ${\overrightarrow{u}}_{\text{child }}$ 计算如下：

$${\overrightarrow{u}}_{\text{child }}={\overrightarrow{u}}_{\text{parent }}+{\overrightarrow{u}}_n$$

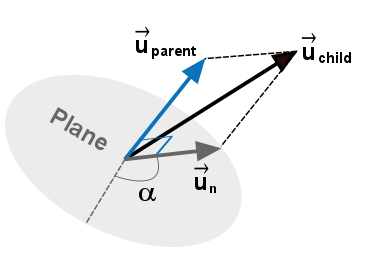
其中，${\overrightarrow{u}}_{\text{parent }}$ 是母滴的速度，而 ${\overrightarrow{u}}_n$ 是在垂直于母滴速度 ${\overrightarrow{u}}_{\text{parent }}$ 的平面内的一种法向速度（参见图12.25：子滴速度（第568页））；其大小表示为：

$$u_n=5\frac{D_{\text{parent }}}{t_b-t_{\text{def }}}$$

图12.25：子液滴速度

对于这五个液滴中的每一个，法向速度方向角 $\alpha$ 在范围 $\left[0,2\pi \right]$ 内随机选择。

破碎后子液滴的目标体积分布由以下根正态分布给出：

$$f\left(D_{\text{child }}\right)=\frac{\sqrt{\frac{D_{\text{child }}}{D_{0.5}}}}{2\sqrt{2\pi }0.238D_{\text{child }}}\exp \left(-\frac{1}{2}{\left(\frac{\sqrt{\frac{D_{\text{child }}}{D_{0.5}}}-1}{0.238}\right)}^2\right)$$

(12.458)

其中，$D_{0.5}=1.2D_{SMD}$，表示破碎后与目标Sauter平均直径相关的质量中位直径，具体如下：

$$D_{SMD}=1.5\frac{O{h}^{0.2}}{W{e}_{corr}^{0.25}}{D}_{\text{parent }}$$

其中，$Oh$ 表示的是 Ohnesorge 数，其定义为：

$$Oh=\frac{{\mu }_l}{\sqrt{{\rho }_l{D}_{\text{ref }}{\sigma }_l}}$$

(12.460)

此处，${\mu }_1$ 表示液滴的粘度，${\sigma }_1$ 表示液滴的表面张力，而 $D_{\text{ref }}$ 则是由以下公式给出的变形液滴的参考面积：

$$D_{ref}=\{\begin{array}{ll}\left(1+0.19\sqrt{We}\right)D_{\text{parent }},& We<100\\ 2.9D_{\text{parent }},& We\ge 100\end{array}$$

(12.461)

其中，$W{e}_{\text{corr}}$ 是针对高液滴粘度（即 $\left(Oh>0.1\right)$）修正后的韦伯数；其计算方式如下：

$$W{e}_{\text{corr }}=\frac{We}{1+1.0770h^{1.6}}$$

图12.26展示了Madabhushi模型中断裂后子液滴的直径分布与标准正态分布的对比：Madabhushi直径分布（第569页）。

图12.26：Madabhushi直径分布

在柱状断裂后经历二次断裂的液滴代表了现实世界中从液体核心断裂出的液丝。这些液丝形状各异，最终断裂成尺寸不等的小液丝，这些小液丝的尺寸与Pilch和Erdman模型产生的原始子液滴不相同，后者假设母液滴几乎呈球形。Pilch和Erdman断裂模型在这一区域有高估子液滴直径的倾向。为了克服这一不准确性，对在柱状断裂后经历进一步二次断裂的子液滴直径乘以一个因子$F_{Lig}>0$，以考虑液丝的影响：

$$D_{\text{child }}=F_{\text{Lig }}{\bar{D}}_{\text{child }}$$

(12.463)

${\bar{D}}_{child}$ 遵循破碎后子液滴的相同目标体积分布，如公式 12.458 (第 568 页) 所示。

在此机制中，子液滴根据 Pilch 和 Erdman 的模型继续进一步破碎，不考虑子液滴直径的权重 (即 $F_{Lig}=1$ )，直到它们变得非常小，以至于水的表面张力开始形成新液滴，不再发生进一步破碎。

同样的机制 (即 $F_{Lig}=1$ ) 也适用于 WAVE 破碎模型从液体核心剥离的液滴的进一步二次破碎。

12.13.6 Schmehl 破碎模型

Schmehl 破碎模型 [580] (第 1090 页) 区分了三种破碎模式：

• 袋状破碎

• 多模式破碎

• 剪切破碎

这些模式根据韦伯数 (Weber number) 的不同而有所区别，韦伯数是衡量气动力相对于表面张力强度的指标：

$$We=\frac{{\rho }_g{u}_{rel}^2{D}_{\text{parent }}}{{\sigma }_l}$$

（12.464）

以及Ohnesorge数，该数值评估了液滴内粘性摩擦对表面张力的阻尼效应：

$$Oh=\frac{{\mu }_l}{\sqrt{{\rho }_l{D}_{\text{parent }}{\sigma }_l}}$$

在公式12.464（第570页）和公式12.465（第570页）中：

$${\rho }_g=\text{gas density}$$

$u_{\text{rel }}=$ 液滴与气体之间的相对速度

$D_{\text{parent }}=$ 破碎前液滴的直径

${\rho }_l=$ 液滴液体的密度

${\sigma }_l=$ 液滴液体的表面张力

不同破碎机制之间的过渡是通过以下依赖于局部韦伯数的函数来建模的：

• 无破碎的变形：

$$\text{We}\le {\text{We}}_{\text{crit}}=12\left(1+1.0770h^{1.6}\right)$$

• 包拆分：

$$W{e}_{\text{crit }}<\mathrm{We}\le W{e}_{\text{multimode }}=20\left(1+1.200{\text{ oh }}^{1.5}\right)$$

• 多模态分解：

$${\text{We}}_{\text{multimode}}<\frac{\text{We}}{\text{shear}}\text{=32}\left(\text{1 +1}\text{.500}{\text{0 oh}}^{\text{1.4}}\right)$$

剪切断裂：

$$W{e}_{\text{shear }}<\mathrm{We}$$

这三种破碎机制采用了不同的法向速度、破碎时间点和子液滴体积分布。

在所有情况下，破碎过程都细分为两个阶段：

• 液滴初始变形为圆盘形状

• 进一步变形并分解液滴

Schmehl破碎模型采用了Pilch和Erdman[518]（第1087页）提出的变形和分解机制。液滴的变形周期、阻力系数、阻力参考面积以及阻力大小是根据公式12.448（第566页）至公式12.454（第567页）计算得出的（详细内容参见Madabhushi破碎模型（第565页））。

总破碎时间$t_b$取决于局部韦伯数，并由以下相关性确定：

• 对于Ohnesorge数$Oh<1$，使用公式12.455（第567页）。

• 对于Ohnesorge数$Oh\ge 1$，液体粘度主导液滴破碎过程，并使用以下相关性：

$$\frac{t_b}{t^{\ast }}=4.5\left(1+1.20h^{0.74}\right)$$

(12.466)

由于边缘扩张，子液滴速度的计算依据方程12.456（第567页）（参见图12.25：子液滴速度（第568页））。在垂直于母液滴速度${\overrightarrow{u}}_{\text{parent}}$的平面内的法向速度${\overrightarrow{u}}_n$的大小取决于破碎区域：

• 袋状破碎 $\left(W{e}_{\text{crit }}<\mathrm{We}\le W{e}_{\text{multimode }}\right)$ :

$$u_n=\frac{2.5D_{\text{parent }}}{t_b-t_{\text{def }}}$$

(12.467)

• 多模态破碎 $\left(W{e}_{\text{mulimode }}<\mathrm{We}\le W{e}_{\text{shear }}\right)$ :

$$u_n=\frac{2.0D_{\text{parent }}}{t_b-t_{\text{def }}}$$

(12.468)

• 剪切破碎（剪切韦伯数小于临界韦伯数时发生）：

$$u_n=0$$

与Madabhushi模型类似，法向速度方向角$\alpha$在范围$\left[0,2\pi \right]$内随机选择，用于每个子液滴（参见图12.25：子液滴速度（第568页））。子液滴的数量并不固定为五个，如Madabhushi模型中那样。默认情况下，它设置为1，但可以根据《Fluent用户指南》中的“破碎”部分在图形用户界面（GUI）中进行更改。

在Bag破碎和多模式破碎机制中，破碎后子液滴的目标体积分布由根正态分布方程12.458（第568页）给出，该方程源自Madabhushi破碎模型（参见图12.26：Madabhushi直径分布（第569页））。

在Bag破碎机制中，母液滴包的总质量$M_{\text{ parent }}$均匀分布在子液滴包上。在剪切破碎机制中，母液滴包总质量的$20\%$保留在母液滴包中，只有$80\%$均匀分布在子液滴包上。多模式破碎机制介于Bag破碎和剪切破碎机制之间。该机制根据定义破碎机制的韦伯数$W{e}_{mulimode}$和$W{e}_{\text{shear }}$，使用线性插值法计算从两个其他机制中分离出的质量。

在多模式破碎机制$\left(W{e}_{\text{multimode }}<\mathrm{We}\le W{e}_{\text{shear }}\right)$中，保留在母液滴包中的质量$M_{\text{core }}$计算如下：

$$M_{\text{core }}=0.2\frac{We-W{e}_{\text{multimode }}}{W{e}_{\text{shear }}-W{e}_{\text{multimode }}}{M}_{\text{parent }}$$

因此，分布在子液滴包中的均匀质量 $M_{\text{stripped }}$ 计算如下：

$$M_{\text{stripped}}=\left(1-0.2\frac{{\text{We-We}}_{\text{multimode}}}{{\text{We}}_{\text{shear}}-{\text{We}}_{\text{multimode}}}\right)M_{\text{parent}}$$

(12.471)

最终，剩余的母液滴包根据其破碎后子液滴的目标体积分布、新的流量以及包内液滴数量进行调整，这些参数均基于$M_{\text{core }}$计算得出。

在剪切破碎区域，子液滴的体积分布具有双峰密度函数的特征，小直径液滴区域有一个峰值，大直径液滴区域有第二个峰值。液滴碎片的细小部分约占母液滴包总质量$M_{parent}$的$80\%$。这些液滴源于剪切力从盘状液滴上剥离的薄膜碎片。大直径区域剩余的$20\%$代表了剥离过程中形成的核心液滴碎片的贡献。这个核心液滴的直径$D_{\text{crit }}$根据破碎瞬间的流动条件下的临界韦伯数$W{e}_{\text{crit }}$估算如下：

$$D_{\text{crit }}=\frac{W{e}_{\text{crit }}{\sigma }_l}{{\rho }_g{u}_{\text{rel }}^2{D}_{\text{parent }}}$$

(12.472)

破碎后剥离的子液滴的目标体积分布与 Madabhushi 破碎模型方程 12.458（第 568 页）（见图 12.26：Madabhushi 直径分布（第 569 页））中的根正态分布相同；然而，在这里，质量中径直径取为：

• 对于 $D_{\text{crit }}>D_{SMD}$，

$$D_{0.5}=1.2D_{SMD}^{\text{reduced }}$$

(12.473)

其中

$$D_{SMD}^{\text{reduced }}=\frac{4D_{SMD}{D}_{crit}}{5D_{crit}-D_{SMD}}$$

• 对于 $D_{\text{crit }}\le D_{SMD}$ 的情况，

$$D_{0.5}=1.2D_{SMD}$$

如在袋状破碎和多模态破碎机制中那样，

随后，剩余的母液滴包根据新的直径进行调整：

$$D_{\text{parent }}^{\text{new }}=\{\begin{array}{ll}\max \left(D_{\text{crit }},D_{\text{parent }}\right)& \text{ if }{D}_{\text{crit }}>D_{SMD}\\ D_{0.5}& \text{ if }{D}_{\text{crit }}\le D_{SMD}\end{array}$$

并且还包括基于 $M_{\text{core }}=0.2M_{\text{parent }}$ 计算得到的新流量和液滴数量。由于 $D_{\text{crit }}$ 可能大于原始母液滴直径，具体取决于临界韦伯数 $W{e}_{\text{crit }}$，剩余液滴包的最大直径被限制为破碎过程前原始母液滴包的直径。

如果破碎包的数量设为一个，则统计破碎完成，不会产生子液滴包。母液滴包根据新直径、新流量和液滴数量进行调整，如下所示：

• 变形（We $\le W{e}_{\text{crit }}$）：无破碎

• 袋状破碎 $\left(W{e}_{\text{crit }}<\mathrm{We}\le W{e}_{\text{multimode }}\right)$：

$$D_{\text{parent }}^{\text{new }}=D_{0.5}=1.2D_{SMD}$$

(12.477)

• 多模态破碎 $\left(W{e}_{\text{mulimode }}<\mathrm{We}\le W{e}_{\text{shear }}\right)$ :

$$D_{\text{parent }}^{\text{new }}=D_{0.5}=1.2D_{SMD}$$

(12.478)

• 剪切破碎（剪切韦伯数 $W{e}_{\text{shear}}$ 小于临界韦伯数 $We$）：

$$D_{\text{parent }}^{\text{new }}=\{\begin{array}{ll}1.2D_{SMD}^{\text{reduced }}=\frac{4D_{SMD}{D}_{\text{crit }}}{5D_{\text{crit }}-D_{SMD}}& \text{ if }{D}_{\text{crit }}>D_{SMD}\\ D_{0.5}=1.2D_{SMD}& \text{ if }{D}_{\text{crit }}\le D_{SMD}\end{array}$$

(12.479)

新生成的母滴直径与破碎后的目标索特平均直径之间的关系为：

$$D_{SMD}=1.5\frac{O{h}^{0.2}}{W{e}_{\text{corr }}^{0.25}}{D}_{\text{parent }}$$

如上所述，母液滴包层的变形和破碎机制以及由于边缘膨胀引起的速度调整均被应用。