本节介绍尺度自适应模拟（SAS）模型的理论基础。关于在Ansys Fluent中使用该模型的详细信息，请参阅用户指南中的“设置尺度自适应模拟（SAS）建模”部分。

更多信息，请参见以下章节： 4.12.1 概述 4.12.2 SST-SAS模型的传输方程 4.12.3 与其他基于$\omega$​的湍流模型结合的SAS

4.12.1 概述

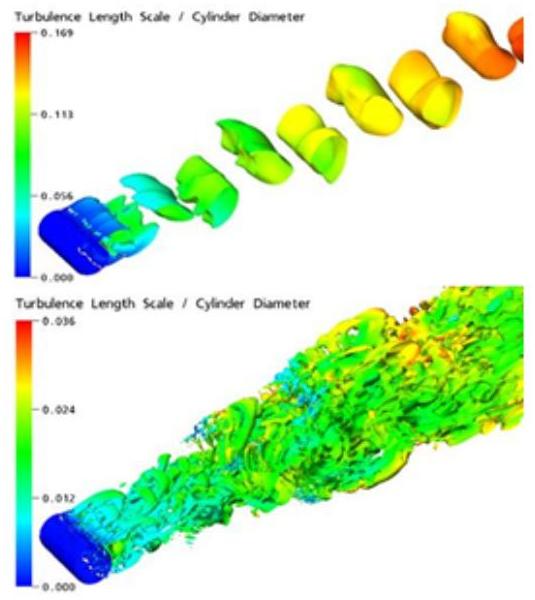
尺度自适应模拟（SAS）是一种改进的URANS公式，它允许在不稳定流动条件下解析湍流谱。图4.6：横流中圆柱的解析结构（顶部：URANS；底部：SST-SAS）（第107页）显示了使用SST模型（URANS）和SST-SAS模型计算的横流中圆柱的等值面，其中$S-\Omega ={10}^{5}1/s^2$（$Re=3.6\ast {10}^6$​）。URANS模拟仅产生大尺度非定常性，而SST-SAS模型以动态方式适应已解析的尺度，并允许在分离区域发展湍流谱。图4.6：横流中圆柱的解析结构（顶部：URANS；底部：SST-SAS）

SAS概念基于将von Kármán长度尺度引入湍流尺度方程。von Kármán长度尺度提供的信息使SAS模型能够动态适应URANS模拟中的已解析结构，从而在流动场的不稳定区域产生类似LES的行为。同时，该模型在稳定流动区域提供标准的RANS功能。 关于入口合成湍流生成的信息，请参阅“尺度解析模拟的入口边界条件”（第126页)。

4.12.2 SST-SAS 模型的输运方程

从基本原理的角度来看，目前使用的所有两方程模型都缺乏一个基础的精确输运方程，该方程可以作为逐项模型开发的指导。这种缺陷的原因在于，$\epsilon$ 的精确方程描述的不是大尺度，而是耗散尺度。然而，两方程模型的目标是对大尺度运动对平均流动的影响进行建模。由于缺乏精确方程，$\epsilon$ 和 $\omega$ 方程是根据湍流动能 $k$ 的方程，使用纯启发式论据进行建模的。Rotta（1968, 1972）开发了一种更一致的方法来制定尺度方程。Rotta 没有使用纯启发式和量纲论据，而是为湍流动能乘以长度尺度 $kL$ 制定了一个精确的输运方程。Rotta 的方程代表了湍流的大尺度，因此可以作为逐项建模的基础。Ansys Fluent 中实现的 SST-SAS 模型的输运方程基于将 Rotta 的方法转换为 $k-\omega$（SST）并定义为： $$\frac{\partial \rho k}{\partial t}+\frac{\partial }{\partial x_i}\left(\rho u_{i}k\right)=G_k-\rho c_{\mu }k\omega +\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]\text{\hspace{1em}(4.263)}$$ $$\begin{array}{rl}\frac{\partial \rho \omega }{\partial t}+\frac{\partial }{\partial x_i}(\rho u_i\omega )& =\alpha \frac{\omega }{k}{G}_k-\rho \beta {\omega }^2+Q_{SAS}+\frac{\partial }{\partial x_i}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\omega }}\right)\frac{\partial \omega }{\partial x_j}\right]\\ & +(1-F_1)\frac{2\rho }{{\sigma }_{\omega ,2}}\frac{1}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j}\end{array}\text{\hspace{1em}(4.264)}$$ 详细推导请参阅 Egorov 和 Menter [431]（第 1082 页）。SST-SAS 模型的传输方程（方程 4.263，第 107 页）和方程 4.264（第 107 页）与 SST RANS 模型 [428]（第 1081 页）的不同之处在于，在湍流涡频率 $\omega$ 的传输方程（方程 4.264，第 107 页）中增加了 SAS 源项 $Q_{SAS}$。在方程 4.264（第 107 页）中，${\sigma }_{\omega ,2}$ 是 SST 模型中 $k-\epsilon$ 区域的 ${\sigma }_{\omega }$ 值。

额外的源项 $Q_{SAS}$ 如下所示（详细内容请参阅 Egorov 和 Menter [431]，第 1082 页）： $$Q_{SAS}=max\left[\rho {\eta }_2\kappa S^2{\left(\frac{L}{L_{\nu \kappa }}\right)}^2-C\cdot \frac{2\rho k}{{\sigma }_{\varphi }}max\left(\frac{1}{{\omega }^2}\frac{\partial \omega }{\partial x_j}\frac{\partial \omega }{\partial x_j},\frac{1}{k^2}\frac{\partial k}{\partial x_j}\frac{\partial k}{\partial x_j}\right),0\right]\text{\hspace{1em}(4.265)}$$ 这个SAS源项源自Rotta输运方程[430]（第1082页）中的二阶导数项。在SAS源项方程4.265（第108页）中的模型参数是... $${\eta }_2=3.51$$ $${\sigma }_{\varphi }=2/3$$ $$C=2$$ 这里，$L$ 代表所模拟湍流的长度尺度。 $$L=\sqrt{k}/\left(c_{\mu }^{1/4}\cdot \omega \right)\text{\hspace{1em}(4.266)}$$ 冯·卡门长度尺度 ( L_{vK} ) 是经典边界层定义的三维推广，即 ( L_{BL}^{vK} = \kappa \frac{\partial U}{\partial y}/\frac{{\partial }^{2}U}{\partial {y}^{2}} )。 $$L_{vK}=\kappa \left|\frac{U^{\prime }}{U^{\prime \prime }}\right|\text{\hspace{1em}(4.267)}$$ 速度的第一个导数 $\frac{\partial U}{\partial y}$ 在 $L_{vK}$ 中由 $U^{\prime }$ 表示，其等于 $S$，即应变率张量 $S_{ij}$ 的标量不变量。 $$U^{\prime }=S=\sqrt{2\cdot S_{ij}{S}_{ij}};S_{ij}=\frac{1}{2}\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\text{\hspace{1em}(4.268)}$$ 请注意，同样的 $S$ 也直接参与了 $Q_{SAS}$（公式 4.265（第 108 页））以及湍流生成项 $P_k={\mu }_t{S}^2$ 中。第二个速度导数 $U^{\prime \prime }$ 通过速度拉普拉斯算子的模来推广到三维： $$U^{\prime \prime }=\sqrt{\frac{{\partial }^2{U}_i}{\partial x_k^2}\frac{{\partial }^2{U}_i}{\partial x_j^2}}\text{\hspace{1em}(4.269)}$$ 因此定义的 $L$ 和 $L_{vK}$ 在边界层的对数部分都等于 $\left(\kappa y\right)$，其中 $\kappa =0.41$ 是冯·卡门常数。 该模型还提供了对高波数阻尼的直接控制。这是通过以下方式对 $L_{vK}$ 值设置较低约束来实现的： $$L_{vK}=\max \left(\kappa \left|\frac{U^{\prime }}{U^{\prime \prime }}\right|,C_S\sqrt{\frac{\kappa {\eta }_2}{\left(\beta /c_{\mu }\right)-\alpha }}\cdot \Delta \right),\Delta ={\Omega }_{CV}^{1/3}\text{\hspace{1em}(4.270)}$$ 此限制器与网格单元尺寸 $\Delta$ 成正比，该尺寸计算为控制体积大小 ${\Omega }_{CV}$ 的立方根。此限制器的目的在于控制对最精细解析湍流脉动的阻尼。限制器的结构来源于对 SST-SAS 模型 [431]（第 1082 页）平衡涡粘性的分析。

4.12.3 与其他基于 $\omega$ 的湍流模型的 SAS

SAS 方法不仅可以与 SST 模型结合，还可以与几种其他基于 $\omega$ 的湍流模型结合：

• 标准 $k-\omega$、BSL $k-\omega$ 和广义 $k-\omega$（GEKO）
• 过渡 SST
• 基于 $\omega$ 的雷诺应力模型（RSM）和显式代数雷诺应力模型（EARSM）

将 SAS 功能添加到这些模型之一中，将在基于 $\omega$ 的方程中启用额外的源项 $Q_{SAS}$（如公式 4.265（第 108 页）所定义）。如果 SAS 功能与 BSL（BSL $k-\omega$、Stress-BSL、WJ-BSL-EARSM）结合，则公式 4.270（第 108 页）中的系数 $\alpha$ 和 $\beta$ 是 BSL 模型的系数。如果与 GEKO 结合，则 $\alpha$ 和 $\beta$ 由 GEKO 模型系数确定。对于所有其他组合，使用 SST 模型的系数。此外，在 SAS 项中，这些系数不包括压缩性效应。