以下各节介绍了辐射模型理论的相关信息：

• 5.3.1 概述与局限性
• 5.3.2 辐射传递方程
• 5.3.3 P-1 辐射模型理论
• 5.3.4 Rosseland 辐射模型理论
• 5.3.5 离散传递辐射模型（DTRM）理论
• 5.3.6 离散坐标（DO）辐射模型理论
• 5.3.7 表面到表面（S2S）辐射模型理论
• 5.3.8 蒙特卡罗（MC）辐射模型理论
• 5.3.9 燃烧流中的辐射
• 5.3.10 选择辐射模型

有关在 Ansys Fluent 中设置和使用辐射模型的信息，请参阅用户指南中的“辐射模型”部分。

5.3.1 概述与局限性

Ansys Fluent 提供了六种辐射模型，允许您在热传递模拟中包含辐射，无论是否存在参与介质。

可以使用以下任一辐射模型，在模型中包括由于辐射引起的表面加热或冷却，以及流体相内由于辐射引起的热源或热汇。

• 离散传递辐射模型（DTRM）[94]（第 1062 页），[589]（第 1091 页）

• P-1 辐射模型 [106]（第 1063 页），[596]（第 1091 页）

• Rosseland 辐射模型 [596]（第 1091 页）

• 表面到表面（S2S）辐射模型 [596]（第 1091 页）

• 离散坐标（DO）辐射模型 [110]（第 1063 页），[538]（第 1088 页）

• 蒙特卡罗（MC）辐射模型

除了这些辐射模型外，Ansys Fluent 还提供了一个太阳负荷模型，允许您在模拟中包括太阳辐射的影响。

非常适合使用辐射传热进行模拟的典型应用包括以下内容：

• 火焰的辐射传热

• 表面到表面的辐射加热或冷却

• 耦合辐射、对流和/或传导传热

• HVAC 应用中通过窗户的辐射，以及汽车应用中的舱内传热分析

在玻璃加工、玻璃纤维拉制和陶瓷加工中，辐射传热在模拟中应予以考虑，尤其是在辐射热流密度

$Q_{rad}=\sigma \left(T_{max}^4-T_{min}^4\right)$，相对于对流或传导传热速率较大时。

通常，这种情况发生在高温环境下，此时辐射热流密度的四次方温度依赖性意味着辐射将占主导地位。

5.3.1.1 DTRM模型的优势与局限

DTRM模型的主要优势有三：它是一个相对简单的模型，可以通过增加射线数量来提高精度，并且适用于广泛的辐射厚度范围。

在使用Ansys Fluent中的DTRM模型时，您应注意以下局限性：

• DTRM假设所有表面都是漫反射的，这意味着表面上的入射辐射反射在固体角度上是各向同性的。

• 不包括散射效应。

• 该实现假设了灰色辐射。

• 使用大量射线解决问题会占用大量CPU资源。

• DTRM与非一致性界面或滑动网格不兼容。

• DTRM不支持并行处理。

5.3.1.2 P-1模型的优势与局限

P-1模型相对于DTRM有几个优势。对于P-1模型，RTE（方程5.56，第188页）是一个扩散方程，易于求解且CPU需求低。该模型包括散射效应。对于光学厚度较大的燃烧应用，P-1模型表现良好。此外，P-1模型可以轻松应用于具有曲线坐标的复杂几何形状。

在使用P-1辐射模型时，您应注意以下限制：

• P-1模型假设所有表面均为漫反射。这意味着表面上的入射辐射反射在立体角上是各向同性的。

• 该模型的实现仅限于灰体辐射或使用灰带模型的非灰体辐射。非灰体实现假设每个波长带内的吸收系数是恒定的。无法使用加权灰气体模型（WSGGM）来指定每个波段的吸收系数。非灰体实现还假设墙体在每个波段内的光谱发射率是恒定的。有关灰带模型的更多信息，请参阅DO模型的优势与局限（第185页）。

• 如果光学厚度较小，根据几何复杂性，可能会导致精度损失。

• P-1模型倾向于高估来自局部热源或热汇的辐射通量。

5.3.1.3 Rosseland模型的优势与局限

Rosseland模型相对于P-1模型有两个优势。由于它不解决入射辐射的额外传输方程（如P-1模型所做的那样），Rosseland模型比P-1模型更快，且需要的内存更少。

Rosseland模型仅适用于光学厚介质。当光学厚度超过3时，推荐使用该模型。请注意，当使用基于密度的求解器时，Rosseland模型不可用；它仅在使用基于压力的求解器时可用。

5.3.1.4 DO模型的优势与局限

DO模型涵盖了从表面到表面辐射到燃烧问题中参与性辐射的整个光学厚度范围。它还允许解决半透明壁面上的辐射问题。对于典型的角度离散化，计算成本适中，内存需求也较为适中。

当前的实现限于灰体辐射或使用灰带模型的非灰体辐射。使用精细角度离散化解决问题的计算可能较为密集。

Ansys Fluent中的非灰体实现适用于参与介质，其光谱吸收系数$a_{\lambda }$在光谱带上呈阶梯式变化，但在带内平滑变化。例如，玻璃表现出这种带状行为。当前的实现不模拟二氧化碳或水蒸气等气体的行为，这些气体在特定的波数上吸收和发射能量[447]（第1083页）。非灰体气体辐射的建模仍然是一个发展中的领域。然而，一些研究人员[181]（第1067页）已经使用灰带模型通过将每个带内的吸收系数近似为常数来模拟气体行为。如果需要，可以在Ansys Fluent中以这种方式使用该实现。

Ansys Fluent中的非灰体实现与所有可以使用DO模型灰体实现的模型兼容。因此，可以包括散射、各向异性、半透明介质和颗粒效应。然而，非灰体实现假设每个波长带内的吸收系数是恒定的。无法使用加权灰气体模型（WSGGM）来指定每个带内的吸收系数。该实现允许指定壁面的光谱发射率。发射率在每个带内被假定为恒定的。

在使用DO辐射模型时，您应注意以下限制：

• DO模型不支持与颗粒（流体-固体）欧拉多相流一起使用。
• DO/能量耦合方法不支持多相模型。
• 非共形接口在带有GPU的加速DO模型中不受支持。有关加速DO模型的更多信息，请参阅《Fluent用户指南》中的“加速离散坐标（DO）辐射计算”。

5.3.1.5 S2S模型的优势与限制

表面到表面（S2S）辐射模型适用于模拟无参与介质的封闭辐射传递（例如，航天器热排斥系统、太阳能收集系统、辐射空间加热器和汽车引擎盖冷却系统）。在这些情况下，参与辐射的方法可能并不总是高效。与DTRM和DO辐射模型相比，尽管视角因子计算本身是CPU密集型的，但S2S模型每次迭代的耗时更短。当发射/吸收表面是多面体单元的多边形面时，视角因子计算的增加时间将尤为明显。

使用S2S辐射模型时，您应注意以下限制：

• S2S模型假设所有表面都是漫反射。

• 实现假设为灰色辐射。

• 随着表面面数的增加，存储和内存需求迅速增加。尽管可以通过使用表面面簇来最小化这一点，但如果使用面对面基来计算视角因子，CPU时间将与使用的簇数无关。

• S2S模型不能用于模拟参与辐射问题。

• 如果您的模型包含对称或周期性边界条件，则不能使用带有Hemicube视角因子方法的S2S模型。

• 使用Cluster to Cluster和Ray Tracing视因子计算的S2S模型不支持周期性非共形界面。

• S2S模型不支持辐射边界区域上的悬挂节点或悬挂节点自适应。

• S2S模型不支持半透明边界。

• 当启用聚类时，视因子文件无法在混合的Windows-Linux平台上写入。

5.3.1.6 MC模型的优势与局限

MC模型能够解决从光学薄（透明）区域到光学厚（扩散）区域的问题，如燃烧。它允许您计算准精确解。虽然与其他可用模型相比，MC模型更为准确，但其计算成本更高。

在使用MC辐射模型时，您应注意以下局限性：

• 对于蒙特卡洛模型，所有感兴趣的物理量都计算为表面或体积平均值。

• 以下显著特性/模型与蒙特卡洛模型支持：

• 支持基于一对一自动配对方法的非共形界面网格，如使用容错网格划分（FTM）工作流程生成的网格。

• 半透明壁面完全不支持壳传导，且在边界源指定的非透明壁面上也不支持，详见MC模型的非透明壁面部分。

• 在使用蒙特卡洛模型时，对称平面和周期边界被视为镜面表面。

• 瞬态。

• 热交换器模型。

• 欧拉-欧拉多相模型（VOF、混合、欧拉模型）。注意：

假定多相的辐射场是均匀的，并且仅求解单一辐射场（不是每相一个）。辐射体材料的性质被假定为各相值的体积分数加权平均。如果多于一个相是透明的，这使得解对网格非常敏感。不透明的相应采用高吸收系数建模。

对于具有小液滴尺寸的分散相（与连续形态不同），不包括来自这些小液滴的散射效应。一般来说，当分散相尺寸相对于网格尺寸变小时，这种方法的准确性会降低。

• 以下功能目前不支持蒙特卡洛模型：

• 2D案例。

• 旋转/移动/重叠网格。

• 切割单元网格。

• 网格中的悬挂节点。

• 薄壁（例如，作为挡板）。

• DPM（离散相模型）。

• 欧拉-拉格朗日多相模型。

• 多孔介质（或NETM模型）。

• 燃烧PDF输运。

• 流动边界/开口的辐射边界源。

• 两个区域之间具有内部边界的两个区域都必须参与辐射。

• 不透明壁面上的辐射边界源不可用各向同性辐射通量选项。

• 具有边界源和壳传导的不透明壁面（如果两者都启用，则禁用壳传导）。

• 具有壳传导的半透明壁面，参见MC模型的不透明壁面。

• 网格自适应不支持蒙特卡洛模型。

5.3.2 辐射传输方程

在位置 $\overrightarrow{r}$ 沿方向 $\overrightarrow{s}$ 的吸收、发射和散射介质的辐射传输方程（RTE）为

$$\frac{dI\left(\overrightarrow{r},\overrightarrow{s}\right)}{ds}+\left(a+{\sigma }_s\right)I\left(\overrightarrow{r},\overrightarrow{s}\right)=a{n}^2\frac{\sigma T^4}{\pi }+\frac{{\sigma }_s}{4\pi }{\int }_0^{4\pi }I\left(\overrightarrow{r},{\overrightarrow{s}}^{\prime }\right)\Phi \left(\overrightarrow{s}\cdot {\overrightarrow{s}}^{\prime }\right)d{\Omega }^{\prime }\text{\hspace{1em}(5.56)}$$

以下是翻译后的中文文本：

$\overrightarrow{r}=$ 位置矢量

$\overrightarrow{s}=$ 方向矢量

${\overrightarrow{s}}^{\prime }=$ 散射方向矢量

$s=$ 路径长度

$a=$ 吸收系数

$n=$ 折射率

${\sigma }_s=$ 散射系数

$\sigma =$ 斯特藩-玻尔兹曼常数 $\left(5.67\times {10}^{-8}\mathrm{W}/{\mathrm{m}}^2-{\mathrm{K}}^4\right)$

$I=$ 辐射强度，取决于位置 $\left(\overrightarrow{r}\right)$ 和方向 $\left(\overrightarrow{s}\right)$

$T=$局部温度

$\Phi =$相位函数

${\Omega }^{\prime }=$立体角

$\left(a+{\sigma }_s\right)s$ 是介质的光学厚度或不透明度。在考虑半透明介质中的辐射时，折射率 $n$ 非常重要。图5.1：辐射传热（第189页）展示了辐射传热的过程。

图5.1：辐射传热

DTRM、P-1、Rosseland、DO 和 MC 辐射模型需要吸收系数 $a$ 作为输入。$a$ 和散射系数 ${\sigma }_s$ 可以是常数，$a$ 也可以是局部 $H_{2}O$ 和 $C{O}_2$ 浓度、路径长度和总压力的函数。Ansys Fluent 提供了加权灰气体模型（WSGGM）来计算可变吸收系数。详情请参见《燃烧流中的辐射》（第217页）。DO 和 MC 实现可以模拟半透明介质中的辐射。对于这类问题，必须提供介质的折射率 $n$ 作为计算的一部分。Rosseland 模型也需要你输入折射率，或者使用默认值 1。

P-1 和 DO 辐射模型针对混合物材料进行求解。混合物的辐射特性，如吸收系数、折射率和散射系数，是基于各相辐射特性的体积分数加权平均计算得出的。

在使用多孔介质模型结合辐射模型的模拟中，能量计算中辐射热流和辐射热源的贡献会根据局部孔隙度进行缩放。需要注意的是，Ansys Fluent 中多孔介质与辐射相互作用的模型处理严格来说仅对非常接近或等于 1.0 的局部流体孔隙度值有效。

5.3.3 P-1 辐射模型理论

P-1 辐射模型是更一般的 P-N 模型的最简单情况，后者基于将辐射强度 $I$ 展开成球谐函数的正交级数 [106]（第 1063 页），[596]（第 1091 页）。本节提供关于 P-1 模型所用方程的详细信息。有关模型设置的信息，请参阅用户指南中的“使用辐射模型”部分。

5.3.3.1 P-1 模型方程

如上所述，P-1 辐射模型是 P-N 模型的最简单情况。在模拟灰体辐射时，如果仅使用级数中的四个项，则可以得到以下关于辐射通量 $q_r$ 的方程：

$$q_r=-\frac{1}{3\left(a+{\sigma }_s\right)-C{\sigma }_s}\nabla G\text{\hspace{1em}(5.57)}$$

其中，$a$ 为吸收系数，${\sigma }_s$ 为散射系数，$G$ 为入射辐射，$C$ 为线性各向异性相函数系数，具体描述如下。引入该参数后，

$$\Gamma =\frac{1}{\left(3\left(a+{\sigma }_s\right)-C{\sigma }_s\right)}\text{\hspace{1em}(5.58)}$$

方程5.57（第190页）简化为

$$q_r=-\Gamma \nabla G\text{\hspace{1em}(5.59)}$$

$G$ 的输运方程为

$$\nabla \cdot \left(\Gamma \nabla G\right)-aG+4a{n}^2\sigma T^4=S_G\text{\hspace{1em}(5.60)}$$

其中，$n$ 是介质的折射率，$\sigma$ 是斯特凡-玻尔兹曼常数，$S_G$ 是用户定义的辐射源。当 P-1 模型激活时，Ansys Fluent 通过求解此方程来确定局部入射辐射。

将方程 5.59（第 190 页）和方程 5.60（第 190 页）结合，得到以下方程：

$$-\nabla \cdot q_r=aG-4a{n}^2\sigma T^4\text{\hspace{1em}(5.61)}$$

(- \nabla \cdot {q}_{r}) 的表达式可以直接代入能量方程，以考虑由于辐射产生的热源（或热汇）。

Ansys Fluent 还支持使用灰带模型进行非灰辐射的建模。对于非灰辐射，方程 5.60（第 190 页）被改写为：

$$\nabla \cdot \left({\Gamma }_{\lambda }\nabla G_{\lambda }\right)-a_{\lambda }{G}_{\lambda }+4a_{\lambda }{n}^2\sigma T^4=S_{G\lambda }\text{\hspace{1em}(5.62)}$$

其中，$G_{\lambda }$ 表示光谱入射辐射，$a_{\lambda }$ 是光谱吸收系数，$n$ 是介质的折射率，$S_{G\lambda }$ 为用户定义的源项，$\sigma$ 是斯特藩-玻尔兹曼常数。${\Gamma }_{\lambda }$ 定义为：

$${\Gamma }_{\lambda }=\frac{1}{\left(3\left(a_{\lambda }+{\sigma }_{s\lambda }\right)-C{\sigma }_{s\lambda }\right)}\text{\hspace{1em}(5.63)}$$

其中，${\sigma }_{s\lambda }$ 是光谱散射系数，而 $C$ 是线性各向异性相函数系数。

波长 ${\lambda }_1$ 和 ${\lambda }_2$ 之间的光谱黑体发射 $\left(G_{b\lambda }\right)$ 表示为

$$G_{b\lambda }=4\left[F\left(0\to n{\lambda }_{2}T\right)-F\left(0\to n{\lambda }_{1}T\right)\right]\sigma T^4\text{\hspace{1em}(5.64)}$$

其中，$F\left(0\to n\lambda T\right)$ 表示在折射率为 $n$ 的介质中，温度为 $T$ 的黑体在波长从 0 到 $\lambda$ 的区间内发射的辐射能量份额。${\lambda }_2$ 和 ${\lambda }_1$ 分别是该波段的上限和下限波长。

光谱辐射通量的计算方法如下：

$$q_{\lambda }=-{\Gamma }_{\lambda }\nabla G_{\lambda }\text{\hspace{1em}(5.65)}$$

能量方程中的辐射源项表示为

$$-\nabla q_r=\sum _{\text{All Bands }}-\nabla q_{r,\lambda }=\sum _{\text{All Bands }}{a}_{\lambda }\left(G_{\lambda }-n^2{G}_{b\lambda }\right)\text{\hspace{1em}(5.66)}$$

5.3.3.2 各向异性散射

P-1 辐射模型包含了对各向异性散射进行建模的能力。Ansys Fluent 通过使用线性各向异性散射相函数来模拟各向异性散射：

$$\Phi \left({\overrightarrow{s}}^{\prime }\cdot \overrightarrow{s}\right)=1+C{\overrightarrow{s}}^{\prime }\cdot \overrightarrow{s}\text{\hspace{1em}(5.67)}$$

以下是翻译后的中文文本：

$\overrightarrow{s}=$散射方向的单位向量

${\overrightarrow{s}}^{\prime }=$入射辐射方向的单位向量

$C=$线性各向异性相函数系数，这是流体的一种特性

$C$的取值范围从-1到1。正值表示更多的辐射能量向前散射而非向后，负值则意味着更多的辐射能量向后散射而非向前。零值定义了各向同性散射（即在所有方向上散射的概率相等），这是Ansys Fluent中的默认设置。只有在确信问题中材料的各向异性散射行为时，才应修改默认值。

5.3.3.3 P-1模型中的颗粒效应

当您的Ansys Fluent模型包含分散的第二相颗粒时，您可以在P-1辐射模型中考虑颗粒的影响。请注意，当存在颗粒时，Ansys Fluent会忽略气相中的散射。也就是说，公式5.68（第191页）假设所有散射都由颗粒引起。

对于包含吸收、发射和散射颗粒的灰度吸收、发射和散射介质，入射辐射的传输方程可以写为：

$$\nabla \cdot \left(\Gamma \nabla G\right)+4\pi \left(a{n}^2\frac{\sigma T^4}{\pi }+E_p\right)-\left(a+a_p\right)G=0\text{\hspace{1em}(5.68)}$$

其中，$E_p$ 表示颗粒的等效发射量，$a_p$ 为等效吸收系数，$n$ 是介质的折射率。这些参数定义如下：

$$E_p=\underset{V\to 0}{\lim }\sum _{n=1}^N{\epsilon }_{pn}{A}_{pn}\frac{\sigma T_{pn}^4}{\pi V}\text{\hspace{1em}(5.69)}$$

以及

$$a_p=\underset{V\to 0}{\lim }\sum _{n=1}^N{\epsilon }_{pn}\frac{A_{pn}}{V}\text{\hspace{1em}(5.70)}$$

在公式5.69（第191页）和公式5.70（第192页）中，${\epsilon }_{pn}$、$A_{pn}$和$T_{pn}$分别代表粒子$n$的发射率、投影面积和温度。求和是对体积$V$中的$N$个粒子进行的。这些量在Ansys Fluent的粒子追踪过程中计算。

粒子$n$的投影面积$A_{pn}$定义为

$$A_{pn}=\frac{\pi d_{pn}^2}{4}\text{\hspace{1em}(5.71)}$$

其中，$d_{pn}$ 表示第 $n^{\text{th }}$ 个颗粒的直径。

方程 5.68（第 191 页）中的量 $\Gamma$ 定义为

$$\Gamma =\frac{1}{3\left(a+a_p+{\sigma }_p\right)}\text{\hspace{1em}(5.72)}$$

在粒子追踪过程中，计算等效粒子散射因子，并将其定义为

$${\sigma }_p=\underset{V\to 0}{\lim }\sum _{n=1}^N\left(1-f_{pn}\right)\left(1-{\epsilon }_{pn}\right)\frac{A_{pn}}{V}\text{\hspace{1em}(5.73)}$$

在此，$f_{pn}$ 是与第 $n^{\text{th}}$ 粒子相关的散射因子。

粒子辐射产生的热源（或热汇）被纳入能量方程如下：

$$-\nabla \cdot q_r=-4\pi \left(a{n}^2\frac{\sigma T^4}{\pi }+E_p\right)+\left(a+a_p\right)G\text{\hspace{1em}(5.74)}$$

5.3.3.4 壁面P-1模型的边界条件处理

在模拟灰体辐射时，为了得到入射辐射方程的边界条件，需要计算外向法向矢量$\overrightarrow{n}$与方程5.59（第190页）的点积：

$$q_r\cdot \overrightarrow{n}=-\Gamma \nabla G\cdot \overrightarrow{n}\text{\hspace{1em}(5.75)}$$

$$q_{r,w}=-\Gamma \frac{\partial G}{\partial n}\text{\hspace{1em}(5.76)}$$

因此，入射辐射的通量 ( G ) 在墙面上等于 (- {q}_{r, w})。墙体的辐射热通量是通过以下边界条件计算的：

$$I_w\left(\overrightarrow{r},\overrightarrow{s}\right)=f_w\left(\overrightarrow{r},\overrightarrow{s}\right)\text{\hspace{1em}(5.77)}$$

$$f_w\left(\overrightarrow{r},\overrightarrow{s}\right)={ϵ}_w\frac{n^2\sigma T_w^4}{\pi }+{\rho }_{w}I\left(\overrightarrow{r},-\overrightarrow{s}\right)\text{\hspace{1em}(5.78)}$$

其中，${\rho }_w$ 表示壁面反射率。随后，采用 Marshak 边界条件来消除角向依赖性 [503]（第 1086 页）：

$${\int }_0^{2\pi }{I}_w\left(\overrightarrow{r},\overrightarrow{s}\right)\overrightarrow{n}\cdot \overrightarrow{s}d\Omega ={\int }_0^{2\pi }{f}_w\left(\overrightarrow{r},\overrightarrow{s}\right)\overrightarrow{n}\cdot \overrightarrow{s}d\Omega \text{\hspace{1em}(5.79)}$$

将公式5.77（第192页）和公式5.78（第192页）代入公式5.79（第193页），并进行积分运算，得到

$$q_{r,w}=-\frac{4\pi {\epsilon }_w\frac{n^2\sigma T_w^4}{\pi }-\left(1-{\rho }_w\right)G_w}{2\left(1+{\rho }_w\right)}\text{\hspace{1em}(5.80)}$$

假设墙壁为漫反射灰表面，则有 ${\rho }_w=1-{\epsilon }_w$，此时方程 5.80（第 193 页）变为：

$$q_{r,w}=-\frac{{\epsilon }_w}{2\left(2-{\epsilon }_w\right)}\left(4n^2\sigma T_w^4-G_w\right)\text{\hspace{1em}(5.81)}$$

方程5.81（第193页）用于计算能量方程和入射辐射方程边界条件中的$q_{r,w}$。

在使用灰带模型时，壁面处的通量可以表示如下（假设壁面为漫反射表面）：

$$q_{\lambda ,w}=-\frac{{\epsilon }_{\lambda ,w}}{2\left(2-{\epsilon }_{\lambda ,w}\right)}\left(4n^2\left[F\left(0\to n{\lambda }_{2}T\right)-F\left(0\to n{\lambda }_{1}T\right)\right]\sigma T^4-G_{\lambda ,w}\right)\text{\hspace{1em}(5.82)}$$

其中，${\epsilon }_{\lambda ,w}$ 是壁面发射率，$q_{\lambda ,w}$ 是壁面处的光谱辐射通量，$G_{\lambda ,w}$ 是壁面处的光谱入射辐射。

5.3.3.5 P-1 模型在流动入口和出口的边界条件处理

流动入口和出口处的净辐射热通量计算方式与上述壁面相同。除非您选择重新定义此边界处理，否则 Ansys Fluent 默认所有流动入口和出口的发射率为 1.0（黑体吸收）。

Ansys Fluent 提供了一个选项，允许您在入口和出口处为辐射和对流使用不同的温度。当入口或出口外部的温度与封闭体内的温度有显著差异时，这可能非常有用。有关详细信息，请参阅《用户指南》中的“定义辐射边界条件”。

5.3.4 Rosseland 辐射模型理论

Rosseland 或辐射扩散近似在介质光学厚度较大时有效 $\left(\left(a+{\sigma }_s\right)L\gg 1\right)$，建议在光学厚度大于 3 的问题中使用。它可以从 P-1 模型方程中通过一些近似推导出来。本节提供 Rosseland 模型中使用的方程的详细信息。有关设置模型的信息，请参阅《用户指南》中的“使用辐射模型”。

5.3.4.1 Rosseland 模型方程

与 P-1 模型一样，灰色介质中的辐射热通量矢量可以由方程 5.59（第 190 页）近似表示：

$$q_r=-\Gamma \nabla G\text{\hspace{1em}(5.83)}$$

其中，$\Gamma$ 由方程 5.58（第 190 页）给出。

Rosseland 辐射模型与 P-1 模型不同之处在于，Rosseland 模型假设强度为气体温度下的黑体强度。（P-1 模型实际上计算了 $G$ 的输运方程。）因此，$G=\frac{4\sigma }{n^2}{T}^4$，其中 $n$ 是折射率。将这个 $G$ 值代入方程 5.83（第 194 页）得到

$$q_r=-16\sigma \Gamma n^2{T}^3\nabla T\text{\hspace{1em}(5.84)}$$

既然辐射热流的形式与傅里叶导热定律相同，我们就可以将其表达为：

$$q=q_c+q_r\text{\hspace{1em}(5.85)}$$

$$q=-\left(k+k_r\right)\nabla T\text{\hspace{1em}(5.86)}$$

$$k_r=16\sigma \Gamma n^2{T}^3\text{\hspace{1em}(5.87)}$$

其中，$k$ 表示热导率，而 $k_r$ 则是辐射热导率。方程 5.85（第194页）被用于能量方程中，以计算温度场。

5.3.4.2 各向异性散射

Rosseland 模型允许各向异性散射，采用了与 P-1 模型（第191页）在各向异性散射部分描述的相同相函数（方程 5.67，第191页）。

5.3.4.3 壁面边界条件处理

由于扩散近似在靠近壁面处不再有效，因此需要使用温度滑移边界条件。壁面边界处的辐射热流 $q_{r,w}$ 通过滑移系数 $\psi$ 来定义：

$$q_{r,w}=-\frac{\sigma \left(T_w^4-T_g^4\right)}{\psi }\text{\hspace{1em}(5.88)}$$

其中，$T_w$ 表示壁面温度，$T_g$ 表示壁面处气体的温度，而滑移系数 $\psi$ 则通过拟合[596]（第1091页）中给出的图表曲线来近似。

$$\psi =\{\begin{array}{cc}1/2& N_w<0.01\\ \frac{2x^3+3x^2-12x+7}{54}& 0.01\le N_w\le 10\\ 0& N_w>10\end{array}\text{\hspace{1em}(5.89)}$$

其中，$N_w$ 表示壁面处的导热至辐射参数：

$$N_w=\frac{k\left(a+{\sigma }_s\right)}{4\sigma T_w^3}\text{\hspace{1em}(5.90)}$$

(5.90)

其中 $x={\log }_{10}{N}_w$。

5.3.4.4 流动入口和出口的边界条件处理

对于Rosseland模型，流动入口和出口不需要特殊处理。这些边界处的辐射热流可以使用公式5.85（第194页）来确定。

5.3.5 离散传递辐射模型（DTRM）理论

DTRM的主要假设是，表面元素在一定范围内的立体角内离开的辐射可以用单条射线近似。本节提供DTRM中使用的方程的详细信息。有关设置模型的信息，请参阅用户指南中的“设置DTRM”。

5.3.5.1 DTRM方程

辐射强度 $dI$ 沿路径 $ds$ 的变化方程可以写为

$$\frac{dI}{ds}+aI=\frac{a\sigma T^4}{\pi }\text{\hspace{1em}(5.91)}$$

其中

$a=$ 气体吸收系数

$I=$ 强度

$T=$ 气体局部温度

$\sigma =$ 斯特藩-玻尔兹曼常数 $5.669\times 10^{-8}W/({\mathrm{m}}^2\cdot {\mathrm{K}}^4)$

在此，假设折射率为单位值。DTRM 沿从边界面发出的系列射线积分方程 5.91（第 195 页）。如果 $a$ 沿射线恒定，则 $I\left(s\right)$ 可以估计为 $$I\left(s\right)=\frac{\sigma T^4}{\pi }\left(1-e^{-as}\right)+I_0{e}^{-as}\text{\hspace{1em}(5.92)}$$

其中 $I_0$ 是增量路径起点的辐射强度，由适当的边界条件确定（参见下面的边界条件描述）。然后通过累加穿过流体控制体积的每条射线路径上的强度变化来计算流体中的辐射能量源。

DTRM 中使用的“射线追踪”技术可以在不进行显式视角因子计算的情况下预测表面间的辐射热传递。模型的准确性主要受追踪射线数量和计算网格的限制。

5.3.5.2 射线追踪

在进行流体流动计算之前，光线路径会被计算并存储起来。在每个辐射面，光线会以离散的极角和方位角值发射（参见图5.2：定义点P周围半球立体角的角θ和φ（第196页））。为了覆盖辐射半球，θ从0变化到$\frac{\pi }{2}$，φ从0变化到$2\pi$。然后，每条光线会被追踪以确定它所截取的控制体积以及在每个控制体积内的长度。这些信息随后会被存储在辐射文件中，该文件必须在流体流动计算开始之前读入。

图5.2：定义点P周围半球立体角的角θ和φ

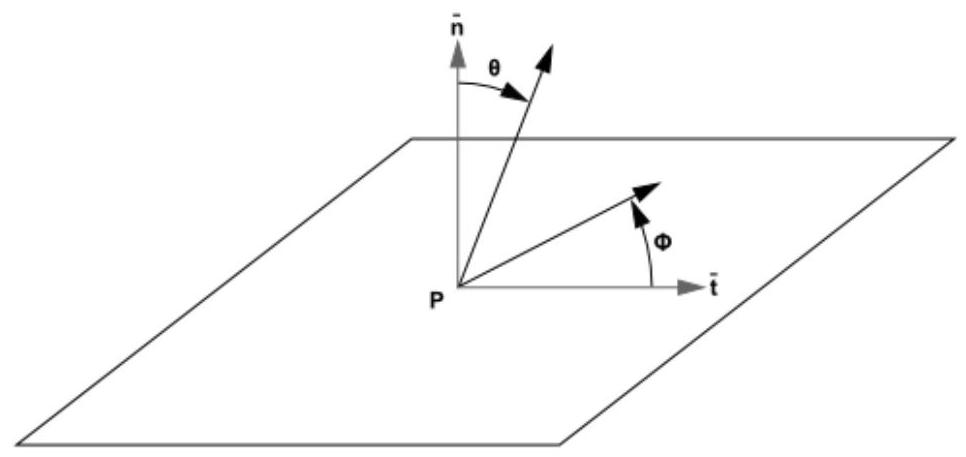
5.3.5.3 聚类

当需要从太多表面追踪光线并且光线穿越太多体积时，DTRM的计算成本非常高。为了减少计算时间，通过将表面和单元聚类成表面和体积“聚类”，减少了辐射表面和吸收单元的数量。体积聚类的形成是从一个单元开始，简单地添加其邻居及其邻居，直到收集到每个体积聚类的指定单元数量。类似地，表面聚类是通过从一个面开始，添加其邻居及其邻居，直到收集到每个表面聚类的指定面数量来形成的。

入射辐射通量 $q_{i{n}^{\prime }}$ 以及体积源项分别针对表面和体积簇进行计算。随后，这些数值被分配到簇中的各个面和单元上，以计算壁面和单元的温度。由于辐射源项具有高度非线性（与温度的四次方成正比），因此在计算表面和体积簇的平均温度时必须十分谨慎，并确保将通量和源项合理地分配给构成簇的面和单元。

表面和体积簇的温度通过面积和体积加权平均获得，具体如以下方程所示： $$T_{sc}={\left(\frac{\sum _f{A}_f{T}_f^4}{\sum A_f}\right)}^{1/4}\text{\hspace{1em}(5.93)}$$

$$T_{vc}={\left(\frac{\sum _c{V}_c{T}_c^4}{\sum V_c}\right)}^{1/4}\text{\hspace{1em}(5.94)}$$

其中，$T_{sc}$ 和 $T_{vc}$ 分别表示表面和体积簇的温度，$A_f$ 和 $T_f$ 是面 $f$ 的面积和温度，$V_c$ 和 $T_c$ 是单元 $c$ 的体积和温度。求和运算是对表面簇的所有面和体积簇的所有单元进行的。

5.3.5.4 壁面处DTRM边界条件的处理

辐射强度接近壁面上的某一点时，通过积分得到入射辐射热流密度 $q_{in}$，即 $$q_{in}={\int }_{\overrightarrow{s}\cdot \overrightarrow{n}>0}{I}_{in}\overrightarrow{s}\cdot \overrightarrow{n}d\Omega \text{\hspace{1em}(5.95)}$$

其中，$\Omega$ 是半球立体角，$I_{in}$ 是入射光线的强度，$\overrightarrow{s}$ 是光线方向向量，$\overrightarrow{n}$ 是向外指向的法线。表面净辐射热流密度 $q_{\text{out}}$ 则计算为 $q_{\text{in}}$ 的反射部分与表面发射功率之和： $$q_{out}=\left(1-{\epsilon }_w\right)q_{in}+{\epsilon }_w\sigma T_w^4\text{\hspace{1em}(5.96)}$$

其中，$T_w$ 是表面 $P$ 处的表面温度，${\epsilon }_w$ 是墙体发射率，您可以将其作为边界条件输入。Ansys Fluent 在预测墙体表面温度时，会考虑辐射热流（公式 5.96，第 197 页）。公式 5.96（第 197 页）还为从点 $P$ 发出的射线的辐射强度 $I_0$ 提供了表面边界条件，即 $$I_0=\frac{q_{\text{out }}}{\pi }\text{\hspace{1em}(5.97)}$$

5.3.5.5 流动入口和出口处的 DTRM 边界条件处理

流动入口和出口处的净辐射热流计算方式与上述墙体相同。除非您选择重新定义此边界处理，否则 Ansys Fluent 假定所有流动入口和出口的发射率为 1.0（黑体吸收）。

Ansys Fluent 提供了一个选项，允许您在入口和出口处使用不同的温度进行辐射和对流。当入口或出口外的温度与封闭体内的温度有较大差异时，这可能非常有用。详细信息请参阅用户指南中的“定义辐射边界条件”。

5.3.6 离散坐标（DO）辐射模型理论

离散坐标 (DO) 辐射模型为有限数量的离散立体角求解辐射传递方程 (RTE)，每个立体角与固定在全局笛卡尔坐标系 $\left(x,y,z\right)$ 中的向量方向 $\overrightarrow{s}$ 相关联。您可以控制角离散的精细程度，类似于选择 DTRM 的光线数量。然而，与 DTRM 不同，DO 模型不执行光线追踪。相反，DO 模型将方程 5.56（第 188 页）转换为空间坐标 $\left(x,y,z\right)$ 中辐射强度的传输方程。DO 模型为每个方向 $\overrightarrow{s}$ 求解尽可能多的传输方程。求解方法与用于流体流动和能量方程的方法相同。

Ansys Fluent 中有两种 DO 模型实现：解耦和（能量）耦合。解耦实现本质上是顺序的，并使用称为有限体积方案的 DO 模型的保守变体 [110]（第 1063 页），[538]（第 1088 页），以及其对非结构化网格的扩展 [466]（第 1084 页）。在解耦情况下，能量和辐射强度方程逐个求解，假设其他变量的当前值。

或者，在耦合坐标方法（或 COMET）[415]（第 1081 页）中，每个单元格的离散能量和强度方程同时求解，假设空间邻居是已知的。

使用耦合方法的优点是它加快了涉及高光学厚度或高散射系数的应用。当使用顺序方法时，此类应用会大幅减慢收敛速度。有关设置模型的信息，请参阅用户指南中的设置 DO 模型。

5.3.6.1 DO 模型方程

DO模型将辐射传输方程（RTE）在方向$\overrightarrow{s}$上视为场方程。因此，方程5.56（第188页）可以写成： $$\begin{array}{rl}\nabla \cdot (I(\vec{r},\vec{s})\vec{s})+(a+{\sigma }_s)I(\vec{r},\vec{s})& =a{n}^2\frac{\sigma T^4}{\pi }\\ & +\frac{{\sigma }_s}{4\pi }{\int }_0^{4\pi }I(\vec{r},{\vec{s}}^{{}^{\prime }})\Phi (\vec{s}\cdot {\vec{s}}^{{}^{\prime }})d{\Omega }^{{}^{\prime }}\end{array}\text{\hspace{1em}(5.98)}$$

Ansys Fluent还允许使用灰带模型对非灰辐射进行建模。光谱强度$I_{\lambda }\left(\overrightarrow{r},\overrightarrow{s}\right)$的RTE可以写成[[448]（第1083页）方程9.22]： $$\begin{array}{rl}\nabla \cdot \left(I_{\lambda }\right(\vec{r},\vec{s}\left)\vec{s}\right)+(a_{\lambda }+{\sigma }_s)I_{\lambda }(\vec{r},\vec{s})& =a_{\lambda }{I}_{b\lambda }\\ & +\frac{{\sigma }_s}{4\pi }{\int }_0^{4\pi }{I}_{\lambda }(\vec{r},{\vec{s}}^{{}^{\prime }})\Phi (\vec{s}\cdot {\vec{s}}^{{}^{\prime }})d{\Omega }^{{}^{\prime }}\end{array}\text{\hspace{1em}(5.99)}$$

这里$\lambda$是波长，$a_{\lambda }$是光谱吸收系数，$I_{b\lambda }$是根据普朗克函数给出的黑体强度。散射系数、散射相函数和折射率$n$被假定为与波长无关。

非灰度离散坐标(DO)实现方法将辐射光谱划分为$N$个波长带，这些波长带不需要连续或范围相等。波长间隔由用户提供，对应真空中的值$\left(n=1\right)$。对每个波长间隔内的辐射传输方程(RTE)进行积分，得到波长带$\Delta \lambda$中包含的辐射能量$I_{\lambda }\Delta \lambda$的传输方程。假设每个波长带内的行为是灰度的。单位立体角内波长带中的黑体发射量可以写成 $$\left[F\left(0\to n{\lambda }_{2}T\right)-F\left(0\to n{\lambda }_{1}T\right)\right]n^2\frac{\sigma T^4}{\pi }\text{\hspace{1em}(5.100)}$$

其中$F\left(0\to n\lambda T\right)$是黑体在温度$T$下，在折射率为$n$的介质中，从0到$\lambda$波长间隔内发射的辐射能量份额[447]（第1083页）。${\lambda }_2$和${\lambda }_1$是波长带的边界。

在位置$\overrightarrow{r}$处，沿方向$\overrightarrow{s}$的总强度$I\left(\overrightarrow{r},\overrightarrow{s}\right)$通过以下公式计算 $$I\left(\overrightarrow{r},\overrightarrow{s}\right)=\sum _k{I}_{{\lambda }_k}\left(\overrightarrow{r},\overrightarrow{s}\right)\Delta {\lambda }_k\text{\hspace{1em}(5.101)}$$

其中求和是对波长带进行的。

非灰度DO模型的边界条件是按波长带应用的。波长带内的处理与灰度DO模型相同。

5.3.6.2 能量耦合与DO模型

在单元格中能量与辐射强度的耦合（也称为COMET）[415]（第1081页）加速了辐射传热有限体积方案的收敛。这种方法显著改善了光学厚度大于10的应用中的收敛性，这在玻璃熔化应用中通常会遇到。当散射显著时，这一特性具有优势，因为它导致了方向性辐射强度之间的强耦合。在Ansys Fluent中，通过在辐射模型对话框中为DO模型启用DO/能量耦合选项来实现这一DO模型实施。耦合方法的离散能量方程如下所示。

当能量方程在控制体积$i$上积分时，得到离散能量方程： $$\sum _{j=1}^N{\mu }_{ij}^T{T}_j-{\beta }_i^T{T}_i={\alpha }_i^T\sum _{k=1}^L{I}_i^k{\omega }_k-S_i^T+S_i^h\text{\hspace{1em}(5.102)}$$

其中 $${\alpha }_i^T=\kappa \Delta V_i$$

$${\beta }_i^T=16\kappa \sigma T_i^{\ast 3}\Delta V_i$$

$$S_i^T=12\kappa \sigma T_i^{\ast 4}\Delta V_i$$

$\kappa =$ 吸收系数

$\Delta V$ 控制体积

系数 ${\mu }_{ij}^r$ 和源项 $S_i^h$ 是由于对对流和扩散项以及非辐射源项的离散化产生的。

结合方程 5.98（第 198 页）的离散形式和能量方程 5.102（第 199 页）的离散形式，得到 [415]（第 1081 页）： $${\overrightarrow{P}}_i{\overrightarrow{q}}_i+{\overrightarrow{r}}_i=0\text{\hspace{1em}(5.103)}$$

其中 $${\overrightarrow{q}}_i=\left[\begin{array}{c}{I}_i^1\\ I_i^2\\ ⋮\\ ⋮\\ I_i^L\\ T_i\end{array}\right]\text{\hspace{1em}(5.104)}$$

$${\overrightarrow{P}}_i=\left[\begin{array}{ccc}{M}_{ii}^1+{\eta }_i^{11}+{\gamma }_i^1{\omega }_1& {\eta }_i^{12}+{\gamma }_i^1{\omega }_2& \dots {\beta }_i^1\\ {\eta }_i^{21}+{\gamma }_i^2{\omega }_1& M_{ii}^2+{\eta }_i^{22}+{\gamma }_i^2{\omega }_2& \dots {\beta }_i^2\\ ⋮& & \\ -{\alpha }_i^T{\omega }_1& -{\alpha }_i^T{\omega }_2& \dots M_{ii}^T\end{array}\right]\text{\hspace{1em}(5.105)}$$

$${\overrightarrow{r}}_i=\left[\begin{array}{c}\sum _{j=1,i\ne j}^N{\mu }_{ij}^l{I}_j^l-S_i^1-S_i^B\\ ⋮\\ ⋮\\ \sum _{j=1,i\ne j}^N{\mu }_{ij}^T{T}_j+S_i^T+S_i^h\end{array}\right]\text{\hspace{1em}(5.106)}$$

5.3.6.2.1 DO/能量耦合的局限性

在某些情况下，不建议或无法使用DO/能量耦合，或者它与某些模型不兼容：

• 对于能量与定向辐射强度耦合较弱的情况，不建议使用DO/能量耦合。这可能导致耦合方法的收敛速度比顺序方法慢。

• 在求解焓方程而非温度方程时，无法使用DO/能量耦合。具体来说，DO/能量耦合与非预混或部分预混燃烧模型不兼容。

要了解如何应用DO/能量耦合，请参阅用户指南中的“设置DO模型”部分。

5.3.6.3 角离散化和像素化

在任何空间位置，角空间 $4\pi$ 的每个八分象限被离散化为 $N_{\theta }\times N_{\phi }$ 个控制角，其范围为 ${\omega }_i$。角度 $\theta$ 和 $\phi$ 分别是极角和方位角，相对于全局笛卡尔坐标系 $\left(x,y,z\right)$ 进行测量，如图5.3所示：角坐标系（第200页）。控制角的 $\theta$ 和 $\phi$ 范围，即 $\Delta \theta$ 和 $\Delta \phi$，是恒定的。在二维计算中，由于对称性，仅求解四个八分象限，总共为 $4N_{\theta }{N}_{\phi }$ 个方向。在三维计算中，总共求解 $8N_{\theta }{N}_{\phi }$ 个方向。对于非灰模型，每个波段求解 $4N_{\theta }{N}_{\phi }$ 或 $8N_{\theta }{N}_{\phi }$ 个方程。

图5.3：角坐标系

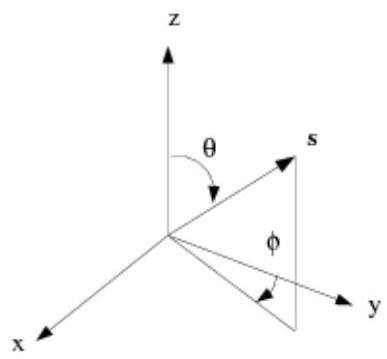
使用笛卡尔网格时，可以将全局角离散化与控制体面边缘对齐，如图5.4所示：无控制角悬垂的面（第201页）。然而，对于通用的非结构化网格，控制体面通常不会与全局角离散化对齐，如图5.5所示：有控制角悬垂的面（第201页），这导致了控制角悬垂的问题[466]（第1084页）。

图5.4：无控制角悬垂的面

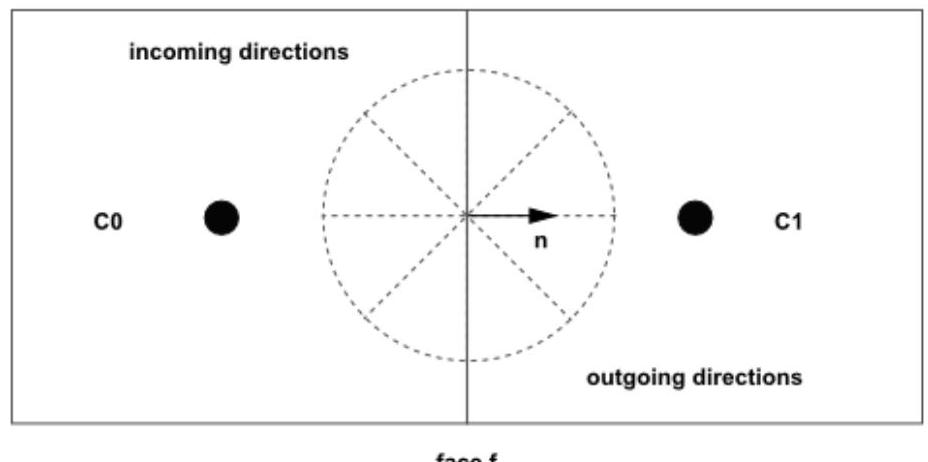
图5.5：有控制角悬垂的面

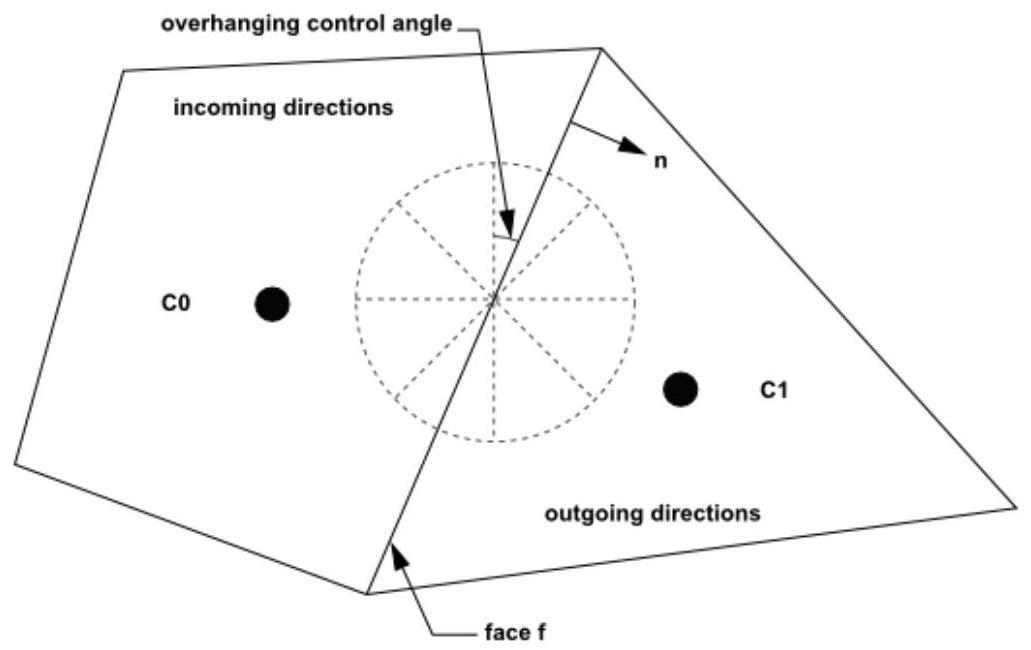
本质上，控制角可以跨越控制体面，使得它们部分朝向面内，部分朝向面外。图5.6：有控制角悬垂的面（3D）（第202页）展示了一个具有控制角悬垂的3D示例。

图5.6：有控制角悬垂的面（3D）

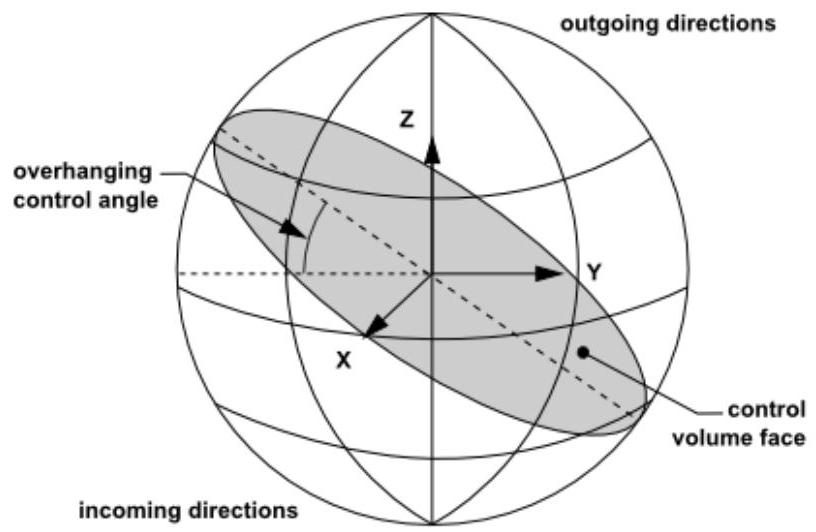
控制体面以任意角度切割代表角空间的球体。交线是一个大圆。控制角悬垂也可能由于反射和折射而发生。在这些情况下，正确计算悬垂部分非常重要。这是通过使用像素化[466]（第1084页）来实现的。

每个悬垂的控制角被分成$N_{{\theta }_p}\times N_{{\phi }_p}$个像素，如图5.7所示：控制角的像素化（第202页）。

图5.7：控制角的像素化

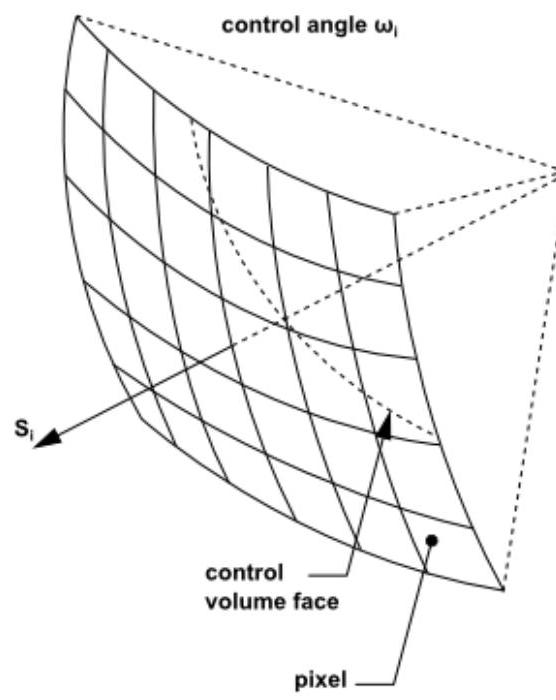
每个像素中包含的能量随后被视为入射或出射到表面。因此，悬垂的影响可以在像素分辨率内得到考虑。Ansys Fluent允许您选择像素分辨率。对于涉及灰漫辐射的问题，默认的$1\times 1$像素化通常已足够。对于涉及对称、周期性、镜面或半透明边界的问题，建议使用$3\times 3$的像素化。然而，您应该意识到增加像素化会增加计算成本。

5.3.6.4 各向异性散射

Ansys Fluent中的DO实现允许使用多种散射相函数。您可以选择各向同性相函数、线性各向异性相函数、Delta-Eddington相函数或用户定义的相函数。线性各向异性相函数在公式5.67（第191页）中描述。Delta-Eddington函数的形式如下： $$\Phi \left(\overrightarrow{s}\cdot {\overrightarrow{s}}^{\prime }\right)=2f\delta \left(1-\overrightarrow{s}\cdot {\overrightarrow{s}}^{\prime }\right)+\left(1-f\right)\left(1+C\overrightarrow{s}\cdot {\overrightarrow{s}}^{\prime }\right)\text{\hspace{1em}(5.106)}$$ 其中，$f$是前向散射因子，$\delta \left(\overrightarrow{s}\cdot {\overrightarrow{s}}^{\prime }\right)$是狄拉克δ函数。$f$项本质上取消了一部分出射散射；因此，对于$f=1$，Delta-Eddington相函数将导致强度表现得好像完全没有散射一样。$C$是不对称因子。当使用Delta-Eddington相函数时，您需要指定$f$和$C$的值。

当使用用户自定义函数来指定散射相函数时，Ansys Fluent 假定相函数的形式为 $$\Phi \left(\overrightarrow{s}\cdot {\overrightarrow{s}}^{{}^{\prime }}\right)=2f\delta \left(1-\overrightarrow{s}\cdot {\overrightarrow{s}}^{{}^{\prime }}\right)+\left(1-f\right){\Phi }^{\ast }\left(\overrightarrow{s}\cdot {\overrightarrow{s}}^{{}^{\prime }}\right)\text{\hspace{1em}(5.108)}$$

用户自定义函数将指定 ${\Phi }^{\ast }$ 和前向散射因子 $f$。

适用于灰体辐射的散射相函数也可用于非灰体辐射。然而，散射能量被限制在同一波段内。

5.3.6.5 DO 模型中的颗粒效应

DO 模型允许您包括离散第二相颗粒对辐射的影响。在这种情况下，Ansys Fluent 将忽略气体中所有其他散射源。

颗粒相的贡献在辐射传递方程（RTE）中表现为： $$\begin{array}{rl}\nabla \cdot (I\vec{s})+(a+a_p+{\sigma }_p)I(\vec{r},\vec{s})& =a{n}^2\frac{\sigma T^4}{\pi }+E_p\\ & +\frac{{\sigma }_p}{4\pi }{\int }_0^{4\pi }I(\vec{r},{\vec{s}}^{{}^{\prime }})\Phi (\vec{s}\cdot {\vec{s}}^{{}^{\prime }})d{\Omega }^{{}^{\prime }}\end{array}\text{\hspace{1em}(5.109)}$$

其中 $a_p$ 是由于颗粒存在而产生的等效吸收系数，由公式 5.70（第 192 页）给出。等效发射 $E_p$ 由公式 5.69（第 191 页）给出。在散射项中使用由公式 5.73（第 192 页）定义的等效颗粒散射因子 ${\sigma }_p$。

对于非灰体辐射，辐射计算中包括了颗粒相在各个波长带内的吸收、发射和散射。颗粒的发射和吸收项也被包含在能量方程中。

5.3.6.6 不透明壁面上的边界和单元区域条件处理

离散坐标辐射模型允许指定域内的不透明壁面（两侧均有相邻的流体或固体区域），或域外的不透明壁面（仅一侧有相邻的流体或固体区域）。如果计算灰体辐射，则不透明壁面被视为灰体；如果使用非灰体DO模型，则被视为非灰体。

图5.8：Ansys Fluent中的不透明壁面上的DO辐射（第204页）展示了一个不透明壁面上辐射的示意图。

图5.8：不透明壁面上的DO辐射

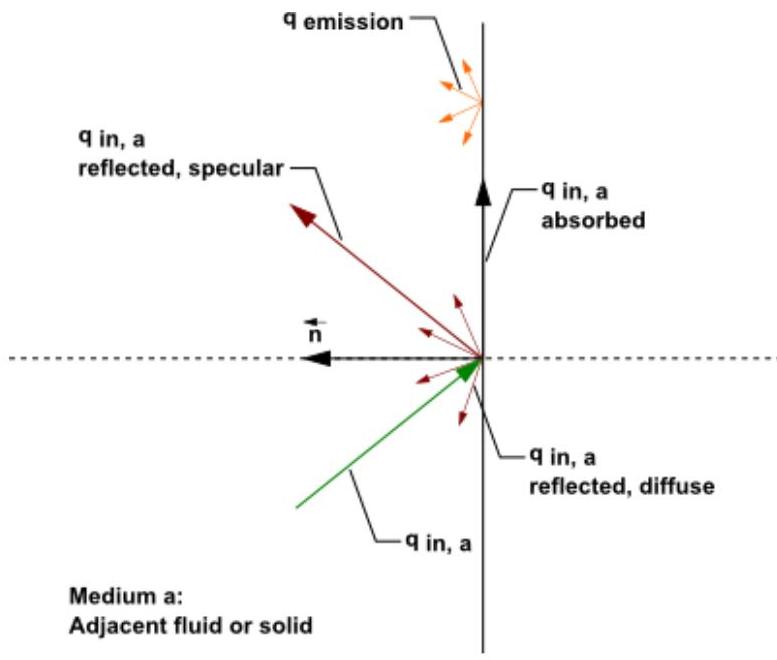
图5.8中的图示显示了不透明壁面a侧的入射辐射$q_{in,a}$。根据您作为边界条件指定的壁面a侧的漫反射分数$f_d$，部分辐射能量会被漫反射和镜面反射。

如图5.8所示，部分入射辐射在壁面表面被吸收，部分辐射从壁面表面发射。壁面表面吸收的入射辐射量和发射回的辐射量取决于该表面的发射率和漫反射分数。对于非灰体DO模型，您必须为每个波长带指定内部发射率。辐射不会通过不透明壁面传输。

撞击不透明墙壁的辐射能量可以被反射回周围介质并被墙壁吸收。反射的辐射可以是漫反射和/或镜面反射，这取决于漫反射分数 $f_d$。如果 $q_{in}$ 是入射到不透明墙壁的辐射能量量，那么 Ansys Fluent 会为不透明墙壁计算以下通用量：

• 墙壁表面的发射能量 $=n^2{\epsilon }_w\sigma T_w^4$

• 漫反射能量 $=f_d\left(1-{\epsilon }_w\right)q_{in}$

• 镜面反射能量 $=\left(1-f_d\right)\left(1-{\epsilon }_w\right)q_{in}$

• 墙壁表面的吸收能量 $={\epsilon }_w{q}_{in}$

其中 $f_d$ 是漫反射分数，$n$ 是相邻介质的折射率，${\epsilon }_w$ 是墙壁发射率，$\sigma$ 是斯特藩-玻尔兹曼常数，$T_w$ 是墙壁温度。

请注意，尽管 Ansys Fluent 在计算辐射量时使用发射率，但在后处理中不可用。墙壁表面的吸收假设吸收率等于发射率。对于纯漫反射墙壁，$f_d$ 等于 1，没有镜面反射能量。类似地，对于纯镜面反射墙壁，$f_d$ 等于 0，没有漫反射能量。介于 0 和 1 之间的漫反射分数将导致部分漫反射和部分反射能量。

5.3.6.6.1 灰漫反射墙壁

对于灰漫反射辐射，入射到墙壁的辐射热流 $q_{i{n}^{\prime }}$ 是

表面离开的净辐射通量由下式给出： $$q_{in}=-{\int }_{4\pi }{I}_{in}\overrightarrow{s}\cdot \overrightarrow{n}d\Omega ,\overrightarrow{s}\cdot \overrightarrow{n}<0\text{\hspace{1em}(5.110)}$$

$$q_{out}=\left(1-{\epsilon }_w\right)q_{in}+n^2{\epsilon }_w\sigma T_w^4\text{\hspace{1em}(5.111)}$$

其中

$n=$ 靠近墙体介质的折射率

${\epsilon }_w=$ 墙体发射率

$\sigma =$ 斯特藩-玻尔兹曼常数

$T_w=$ 墙体温度

此方程对于发射率为0的镜面辐射同样有效。

对于所有从墙体出射的方向$\overrightarrow{s}$，边界强度由下式给出： $$I_0=\frac{q_{\text{out }}}{\pi }\text{\hspace{1em}(5.112)}$$

5.3.6.6.2 非灰体漫反射墙

存在一组特殊的方程，专门适用于非灰体漫反射不透明墙体。这些方程假设墙体表面的吸收率等于发射率。对于非灰体漫反射辐射，在波段$\Delta \lambda$内到达墙体的入射辐射热流$q_{in,\lambda }$为： $$q_{in,\lambda }=\Delta \lambda {\int }_{\overrightarrow{s}\cdot \overrightarrow{n}>0}{I}_{in,\lambda }\overrightarrow{s}\cdot \overrightarrow{n}d\Omega \text{\hspace{1em}(5.113)}$$

在波段$\Delta \lambda$内离开表面的净辐射热流由下式给出： $$q_{\text{out },\lambda }=\left(1-{\epsilon }_{w\lambda }\right)q_{\text{in },\lambda }+{\epsilon }_{w\lambda }\left[F\left(0\to n{\lambda }_2{T}_w\right)-F\left(0\to n{\lambda }_1{T}_w\right)\right]n^2\sigma T_w^4\text{\hspace{1em}(5.114)}$$

其中，${\epsilon }_{w\lambda }$ 表示在该波段内的壁面发射率。$F\left(n,\lambda ,T\right)$ 提供了普朗克分布函数，这定义了每个辐射波段的辐射发射率作为源表面温度的函数。在波段 $\Delta \lambda$ 内的所有出射方向 $\overrightarrow{s}$ 在壁面处的边界强度由下式给出： $$I_{0\lambda }=\frac{q_{\text{out },\lambda }}{\pi \Delta \lambda }\text{\hspace{1em}(5.115)}$$

5.3.6.7 半透明壁面的单元区域和边界条件处理

Ansys Fluent 允许为 DO 模型指定内部和外部半透明壁面。对于内部半透明壁面，入射辐射可以穿过壁面并传输到相邻介质（可能还会发生折射），可以反射回周围介质，并通过壁厚被吸收。透射和反射可以是漫反射和/或镜面反射。您需要为所有透射和反射的辐射指定漫反射分数；其余部分则按镜面反射处理。对于外部半透明壁面，边界壁面上可能有两种辐射源：来自计算域外部的辐照光束和来自相邻流体或固体区域单元的入射辐射。

对于非灰体辐射，半透明壁面边界条件是按波段逐一应用的。一个波段内的辐射能量传输、反射和折射方式与灰体情况相同；不同波段之间的辐射能量不会发生传输、反射或折射。

默认情况下，DO 方程会在所有流体区域中求解，但不会在任何固体区域中求解。因此，如果您有一个与薄壁相邻的固体区域，您需要在 Solid 对话框中将该固体区域指定为参与辐射，作为边界条件设置的一部分。

重要提示：

如果您对半透明介质内部的详细温度分布感兴趣，那么您需要将半透明壁面建模为具有相邻流体区域的固体区域，并将固体视为半透明介质。这一点将在后续章节中讨论。

5.3.6.7.1 半透明内壁

图 5.9：DO 辐射在半透明内壁上的示意图（第 207 页）展示了一个在 Ansys Fluent 中被视为半透明且厚度为零的内（双侧）壁面。由 $q_{in,a}$ 表示的入射辐射能量可以穿过半透明壁面，当且仅当相邻的流体或固体单元区域参与辐射时，从而允许辐射耦合。当一个壁面被指定为半透明时，辐射耦合就会设置。请注意，默认情况下，辐射不会耦合，您需要通过在 Wall 对话框（位于 Radiation 标签下）中将边界条件类型更改为半透明来显式指定内壁的辐射耦合。

图 5.9：DO 辐射在半透明内壁上的示意图

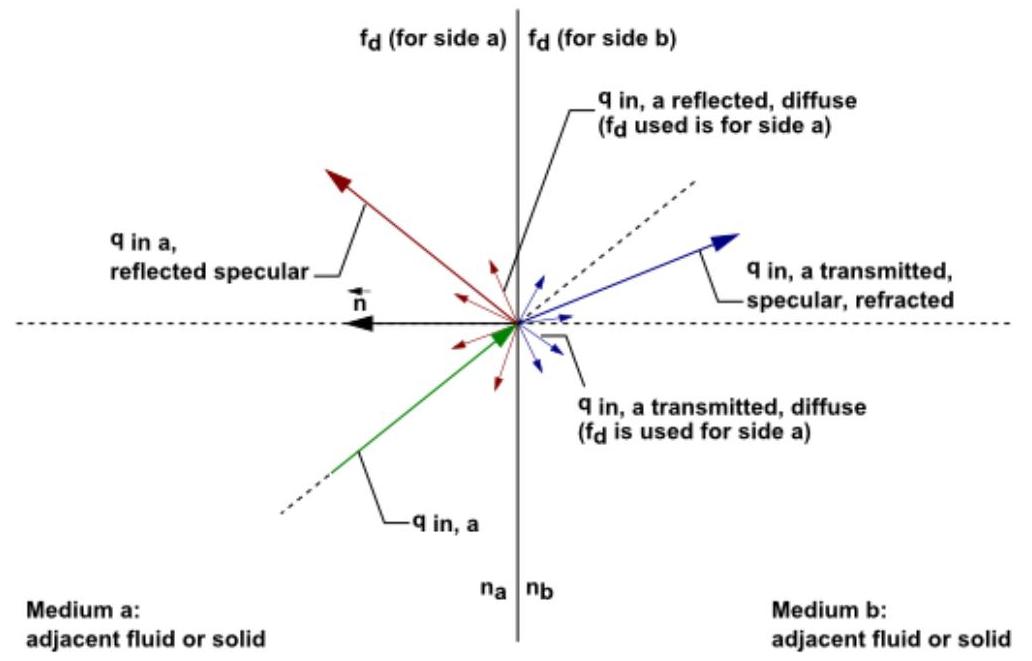
透过半透明壁面传输的入射辐射能可以以镜面方式和漫反射方式传输。如果代表介质$a$的流体区域的折射率$n_a$与介质$b$的折射率$n_b$不同，辐射也可以在内部壁面上反射回周围介质。反射的辐射可以以镜面方式和漫反射方式反射。透射和反射的漫反射辐射与镜面辐射的比例取决于壁面的漫反射分数。纯漫反射和纯镜面透射及反射在半透明壁面上的特殊情况将在以下章节中介绍。注意：

对于零厚度壁面的情况，壁面材料的折射率对折射/反射没有影响，只考虑相邻介质的折射率。

如果半透明壁面具有厚度，那么厚度和吸收系数决定了“薄”壁面的吸收率。如果壁面厚度或吸收系数设置为0，那么壁面没有吸收性。尽管入射辐射可以在具有厚度的半透明壁面中被吸收，但默认情况下，吸收的辐射通量不会影响能量方程，这可能导致能量不平衡，并可能产生意外的温度场。例外情况是使用壳传导（仅在3D中可用）。使用壳传导时，能量和辐射之间存在完全对应关系。如果预计壁面会有显著的吸收/发射，那么在实际操作中，最好用实体单元明确地模拟厚度。Ansys Fluent不包括来自半透明壁面表面的发射（由于定义的内部发射率），除非定义了温度边界条件。

5.3.6.7.2 镜面半透明墙

考虑半透明墙的特殊情况，当漫反射分数 $f_d$ 等于 0 时，半透明墙上所有透射和反射的辐射能均为纯镜面反射。

图 5.10：两种半透明介质界面处的辐射反射和折射（第 208 页）显示了一条从折射率为 $n_a$ 的半透明介质 $a$ 向折射率为 $n_b$ 的半透明介质 $b$ 沿方向 $\overrightarrow{s}$ 传播的光线。界面 $a$ 侧面向介质 $a$；类似地，界面 $b$ 侧面向介质 $b$。界面法线 $\overrightarrow{n}$ 假设指向 $a$ 侧。我们区分界面 $a$ 侧在方向 $\overrightarrow{s}$ 上的强度 $I_a\left(\overrightarrow{s}\right)$ 和界面 $b$ 侧相应的量 $I_b\left(\overrightarrow{s}\right)$。

图 5.10：两种半透明介质界面处的辐射反射和折射

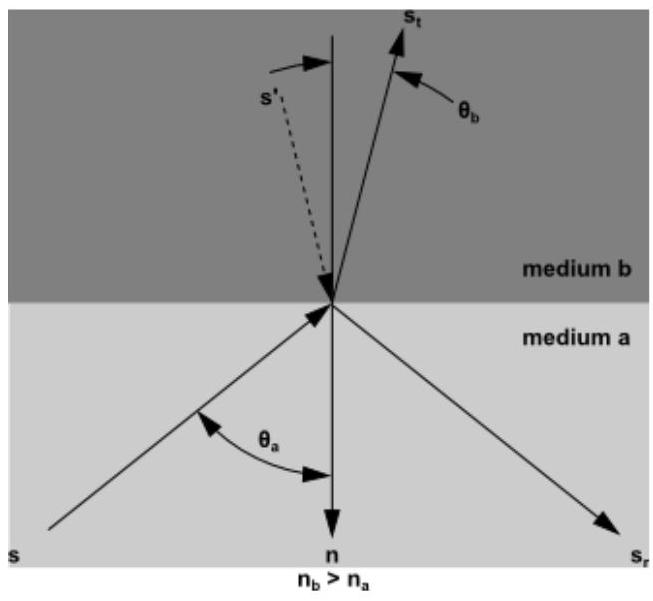
入射到界面的一部分能量被反射，其余部分被透射。反射是镜面的，因此反射辐射的方向由下式给出： $${\overrightarrow{s}}_r=\overrightarrow{s}-2\left(\overrightarrow{s}\cdot \overrightarrow{n}\right)\overrightarrow{n}\text{\hspace{1em}(5.116)}$$

从介质 $a$ 到介质 $b$ 透射的辐射会发生折射。透射能量的方向 ${\overrightarrow{s}}_t$ 由斯涅尔定律给出： $$\sin {\theta }_b=\frac{n_a}{n_b}\sin {\theta }_a\text{\hspace{1em}(5.117)}$$

其中，${\theta }_a$ 是入射角，${\theta }_b$ 是透射角，如图5.10所示：两半透明介质界面处的辐射反射和折射（第208页）。我们还定义了方向 $${\overrightarrow{s}}^{\prime }={\overrightarrow{s}}_t-2\left({\overrightarrow{s}}_t\cdot \overrightarrow{n}\right)\overrightarrow{n}\text{\hspace{1em}(5.118)}$$ 如图5.10所示：两半透明介质界面处的辐射反射和折射（第208页）。界面在侧$a$ [447]（第1083页）的反射率 $$r_a\left(\overrightarrow{s}\right)=\frac{1}{2}{\left(\frac{n_a\cos {\theta }_b-n_b\cos {\theta }_a}{n_a\cos {\theta }_b+n_b\cos {\theta }_a}\right)}^2+\frac{1}{2}{\left(\frac{n_a\cos {\theta }_a-n_b\cos {\theta }_b}{n_a\cos {\theta }_a+n_b\cos {\theta }_b}\right)}^2\text{\hspace{1em}(5.119)}$$ 表示从$\overrightarrow{s}$转移到${\overrightarrow{s}}_r$的入射能量的一部分。

界面侧$a$在出射方向${\overrightarrow{s}}_r$的边界强度$I_{w,a}\left({\overrightarrow{s}}_r\right)$由入射辐射的反射分量和来自侧$b$的透射决定。因此 $$I_{w,a}\left({\overrightarrow{s}}_r\right)=r_a\left(\overrightarrow{s}\right)I_{w,a}\left(\overrightarrow{s}\right)+{\tau }_b\left({\overrightarrow{s}}^{\prime }\right)I_{w,b}\left({\overrightarrow{s}}^{\prime }\right)\text{\hspace{1em}(5.120)}$$

其中，${\tau }_b\left({\overrightarrow{s}}^{\prime }\right)$ 表示在方向 ${\overrightarrow{s}}^{\prime }$ 上界面侧 $b$ 的透射率。类似地，界面侧 $b$ 在方向 ${\overrightarrow{s}}_t$ 上的出射强度 $I_{w,b}\left({\overrightarrow{s}}_t\right)$ 由以下公式给出： $$I_{w,b}\left({\overrightarrow{s}}_t\right)=r_b\left({\overrightarrow{s}}^{\prime }\right)I_{w,b}\left({\overrightarrow{s}}^{\prime }\right)+{\tau }_a\left(\overrightarrow{s}\right)I_{w,a}\left(\overrightarrow{s}\right)\text{\hspace{1em}(5.121)}$$

对于 $n_a<n_b$ 的情况，从介质 $a$ 传输到介质 $b$ 的入射立体角 $2\pi$ 内的能量必须折射进入一个顶角为 ${\theta }_c$ 的锥形区域（参见图 5.11：临界角 $\theta \mathrm{c}$ (第 209 页)），其中

$${\theta }_c={\sin }^{-1}\frac{n_a}{n_b}\text{\hspace{1em}(5.122)}$$

图5.11：临界角 ${\theta }_c$

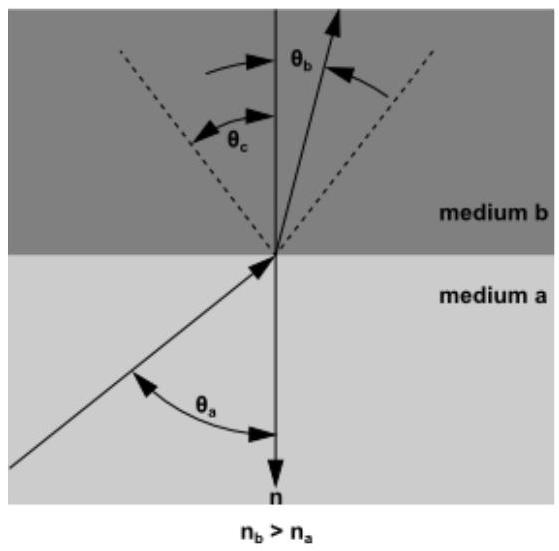
同样地，当辐射能量从介质 $b$ 向介质 $a$ 传输时，在顶角为 ${\theta }_c$ 的圆锥内，其透射分量会被折射到 $2\pi$ 的出射立体角内。对于入射角大于 ${\theta }_c$ 的情况，会发生全内反射，所有入射能量都会镜面反射回介质 $b$。上述方程可以应用于图5.9所示的一般情况：内部半透明墙的DO辐射（第207页）。

当介质 $b$ 位于域外，例如外部半透明墙的情况（图5.12：外部半透明墙的DO辐照（第211页）），$I_{w,b}\left({\overrightarrow{s}}^{\prime }\right)$ 在方程5.120（第209页）中作为边界条件输入的一部分给出。您需要以辐照通量的幅值、光束方向和应用辐射通量的立体角来提供这个入射辐照通量。请注意，外部介质的折射率假定为1。

5.3.6.7.3 漫射半透明墙

考虑半透明墙的特殊情况，当漫射分数 $f_d$ 等于1时，半透明墙上透射和反射的辐射能量完全是漫射的。

在许多工程问题中，半透明界面可能是一个漫反射体。对于这种情况，界面反射率 ( r\left( \overrightarrow{s}\right) ) 被假定为与 (\overrightarrow{s}) 无关，并且等于半球平均值 ( r_d )。对于 ( n = \frac{n_a}{n_b} > 1 )，( r_{d, a} ) 和 ( r_{d, b} ) 由 [597]（第1091页）给出：

[ r_{d, a} = 1 - \frac{\left( 1 - r_{d, b}\right) }{n^2} \tag{5.123} ]

$$\begin{array}{rl}{r}_{d,b=}& \frac{1}{2}+\frac{\left(3n+1\right)\left(n-1\right)}{6{\left(n+1\right)}^2}+\frac{n^2{\left(n^2-1\right)}^2}{{\left(n^2+1\right)}^3}\ln \left(\frac{n-1}{n+1}\right)\\ & -\frac{2n^3\left(n^2+2n-1\right)}{\left(n^2+1\right)\left(n^4-1\right)}+\frac{8n^4\left(n^4+1\right)}{\left(n^2+1\right){\left(n^4-1\right)}^2}\ln \left(n\right)\end{array}\text{\hspace{1em}(124)}$$

界面侧边$a$上所有出射方向的边界强度由下式给出： $$I_{w,a}=\frac{r_{d,a}{q}_{in,a}+{\tau }_{d,b}{q}_{in,b}}{\pi }\text{\hspace{1em}(5.125)}$$

同样地，对于侧边$b$， $$I_{w,b}=\frac{r_{d,b}{q}_{in,b}+{\tau }_{d,a}{q}_{in,a}}{\pi }\text{\hspace{1em}(5.126)}$$

其中 $$q_{in,a}=-{\int }_{4\pi }{I}_{w,a}\overrightarrow{s}\cdot \overrightarrow{n}d\Omega ,\overrightarrow{s}\cdot \overrightarrow{n}<0\text{\hspace{1em}(5.127)}$$

$$q_{in,b}={\int }_{4\pi }{I}_{w,b}\overrightarrow{s}\cdot \overrightarrow{n}d\Omega ,\overrightarrow{s}\cdot \overrightarrow{n}\ge 0\text{\hspace{1em}(5.128)}$$

当中介介质 $b$ 位于计算域外部时，例如外部半透明墙体的情况（图 5.12：外部半透明墙体的 DO 辐照（第 211 页）），$q_{in,b}$ 作为边界条件输入的一部分给出。您需要提供此入射辐照通量的大小、光束方向以及应用辐射通量的立体角。请注意，假设外部介质的折射率为 1。

5.3.6.7.4 部分漫反射半透明墙体

当您为半透明墙体输入的漫反射分数 $f_d$ 介于 0 和 1 之间时，该墙体为部分漫反射和部分镜面反射。在这种情况下，Ansys Fluent 会将漫反射和镜面反射组件的反射和透射辐射通量贡献纳入定义方程中。

5.3.6.7.5 半透明外墙

图 5.12：外部半透明墙体的 DO 辐照（第 211 页）展示了辐照光束 $q_{\text{irrad }}$ 应用于具有零厚度和非零吸收系数的材料属性的外部半透明墙体的一般情况。有关墙体厚度对半透明墙体辐射效应的影响，请参阅上一节。

图 5.12：外部半透明墙体的 DO 辐照

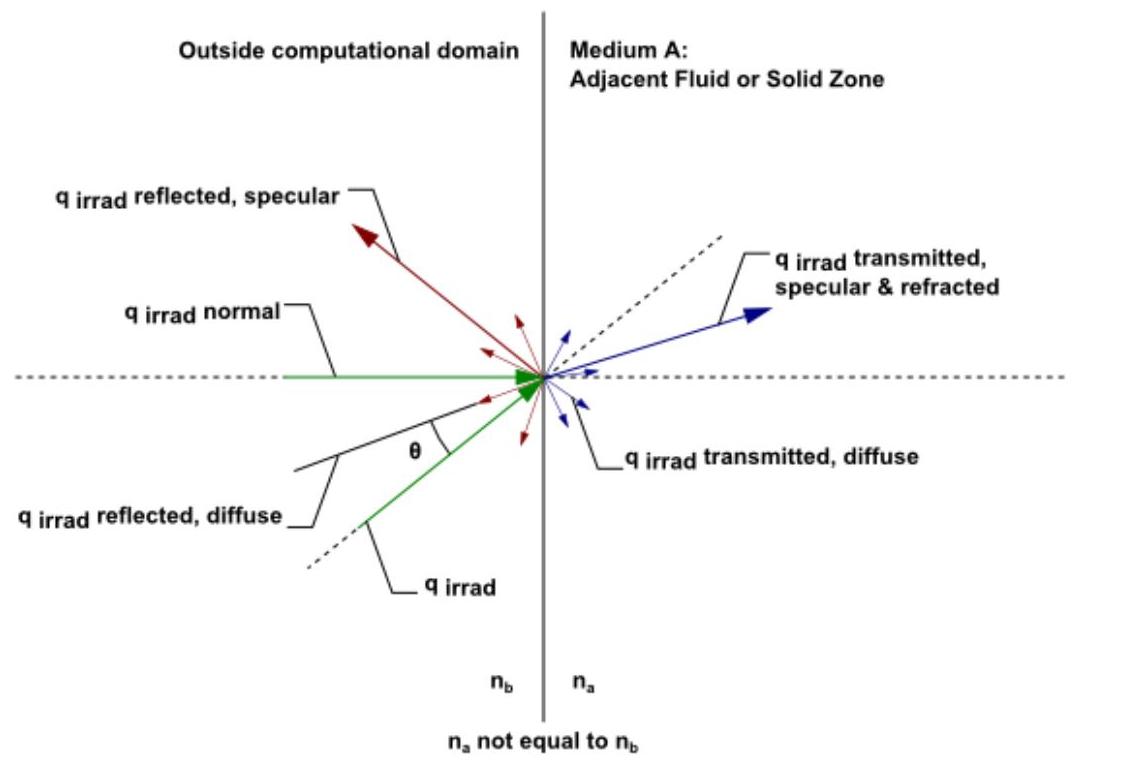
辐射通量从计算域外部穿过半透明壁面（图5.12：外部半透明壁面的DO辐射（第211页））进入相邻的流体或固体介质a。根据您作为边界条件输入的折射指数和漫反射分数，透射辐射可以发生折射（弯曲）并镜面和漫反射。请注意，当壁面的折射指数$\left(n_b\right)$不等于1时，会出现$q_{\text{irrad }}$的反射分量，如所示。

在“热”选项卡中选择混合或辐射壁边界条件时，除了$q_{\text{irrad }}$之外，还会施加一个额外的通量。Ansys Fluent会计算半透明壁面上的这个外部通量。

$$Q_{\text{ext }}={\epsilon }_{\text{external }}\sigma T_{\text{rad }}^4\text{\hspace{1em}(5.129)}$$

进入上述能量域的比例取决于所考虑的半透明墙体的透射率。请注意，这一能量是分布在立体角上的（即，类似于漫反射成分的处理方式）。

入射辐射也可能发生在室外的半透明墙体上。有关详细信息，请参阅之前关于室内墙体的讨论，因为辐射效应是相同的。

辐照光束由您提供的强度、光束方向和光束宽度定义。辐照强度以入射辐射热流密度$\left(W/m^2\right)$的形式指定。光束宽度指定为辐照分布的立体角（即，光束的$\theta$和$\phi$范围）。Ansys Fluent中的默认光束宽度为$1e$ -6度，适用于准直光束辐射。光束方向由立体角中心的矢量定义。如果您在墙体边界条件对话框中选择了“应用与光束平行的直接辐照”功能，那么您需要为辐照提供$q_{\text{irrad }}$（图5.12：外部半透明墙体的DO辐照（第211页）），Ansys Fluent会计算并使用表面法向通量$q_{\text{irrad, normal }}$进行辐射计算。如果未选中此功能，则Fluent会自动应用您指定的源$q_{\text{irrad }}$，使其垂直于边界，从而$q_{\text{irrad }}=$ $q_{irrad,normal}$。

图5.13：外部辐照光束的光束宽度和方向（第212页）展示了辐照光束方向和光束宽度的示意图。您在半透明墙体的边界条件中提供这些输入（以及辐照强度）。

图 5.13：外照射光束的宽度与方向

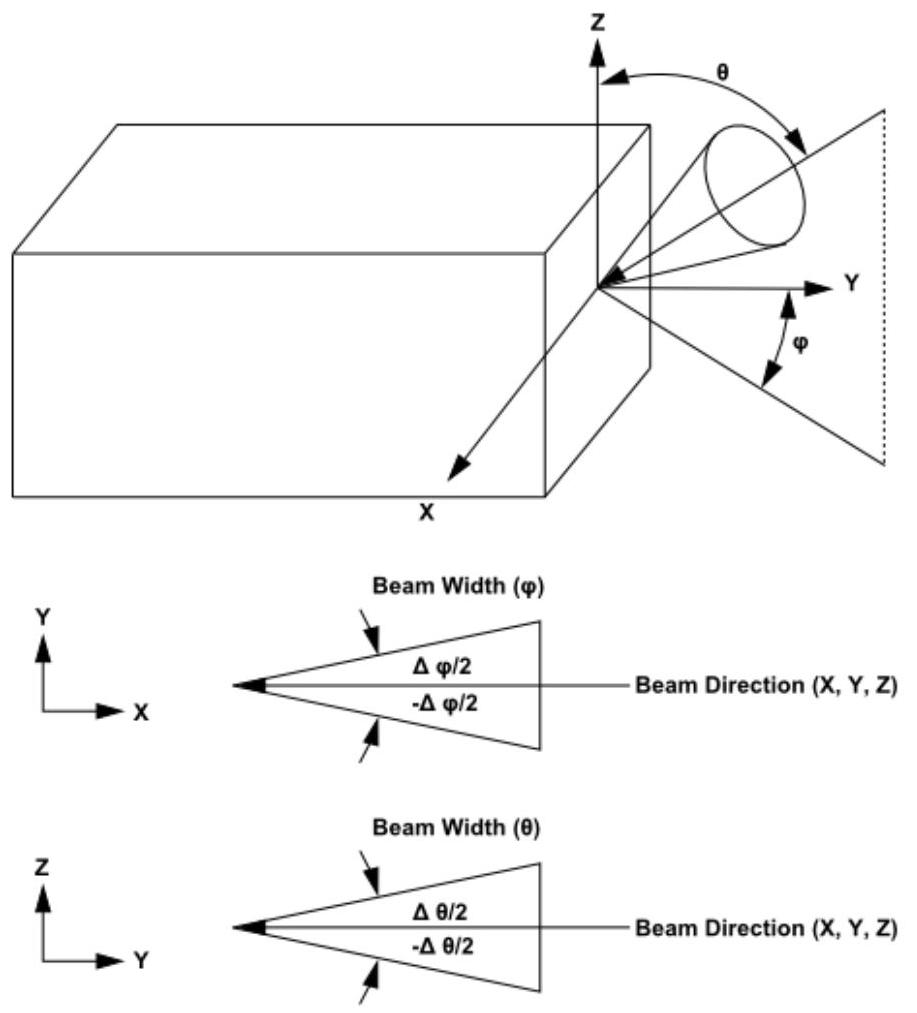
照射光束可根据特定流体或固体区域材料的折射率，在中介a中发生折射。

5.3.6.7.6 限制

在壳传导不活跃的情况下，仅有限支持吸收和发射半透明薄壁的功能。在参与性固体材料中存在显著辐射发射或吸收的情况下，例如玻璃窗对长波辐射的吸收，使用半透明薄壁可能导致数值解中预测出不合理的温度。在三维模型中，可通过激活相应薄壁的壳传导选项来克服这一问题。否则，在可能的情况下，建议通过在壁厚方向上使用一个或多个单元层来明确表示固体壁厚。

5.3.6.7.7 固体半透明介质

离散坐标辐射模型允许您将具有两侧相邻流体或固体区域的固体区域模拟为“半透明”介质。这是通过在边界条件设置中指定固体区域参与辐射来实现的。将固体区域模拟为半透明介质，可以让您获得半透明区域内部的详细温度分布，因为Ansys Fluent在每个单元基础上求解固体能量方程，并提供热结果。然而，默认情况下，DO方程在流体区域中求解，而不是在任何固体区域中。因此，您需要在边界条件设置中，在$\mathbf{Solid}$对话框中指定固体区域参与辐射。

5.3.6.8 镜面壁和对称边界的边界条件处理

在镜面壁和对称边界处，与入射方向$\overrightarrow{s}$对应的反射光线${\overrightarrow{s}}_r$的方向由公式5.116（第208页）给出。此外，

$$I_w\left({\overrightarrow{s}}_r\right)=I_w\left(\overrightarrow{s}\right)\text{\hspace{1em}(5.130)}$$

5.3.6.9 周期性边界的边界条件处理

在使用旋转周期性边界时，采用像素化处理以确保辐射能在周期面和阴影面之间正确传递至关重要。建议像素化范围在 $3\times 3$ 至 $10\times 10$ 之间。

5.3.6.10 流动入口和出口的边界条件处理

对于不透明流动入口和出口，处理方法详见《流动入口和出口的DTRM边界条件处理》(第197页)。

对于透明流动入口和出口，边界行为类似于外部半透明壁面，然而，辐照通量从计算域外通过透明流动边界进入相邻流体区域，过程中不会发生反射、吸收或折射。详细信息请参阅《半透明外部壁面》(第211页)。

5.3.7 表面到表面(S2S)辐射模型理论

表面到表面辐射模型可用于考虑灰-漫射表面封闭体内的辐射交换。两个表面之间的能量交换部分取决于它们的尺寸、分离距离和方向。这些参数通过一个称为“视角因子”的几何函数来考虑。

S2S模型的主要假设是任何辐射的吸收、发射或散射都可以忽略不计；因此，只需考虑“表面到表面”的辐射进行分析。

有关模型设置的信息，请参阅用户指南中的《设置S2S模型》。

5.3.7.1 灰-漫射辐射

Ansys Fluent 中的 S2S 辐射模型假设表面为灰体且漫反射。灰体表面的发射率和吸收率与波长无关。此外，根据基尔霍夫定律 [447]（第 1083 页），发射率等于吸收率 $\left(\epsilon =\alpha \right)$。对于漫反射表面，反射率与出射（或入射）方向无关。

灰体-漫反射模型正是 Ansys Fluent 所采用的模型。如前所述，对于感兴趣的应用，表面间辐射能量的交换实际上不受分隔它们的中介物质的影响。因此，根据灰体模型，如果有一定量的辐射能量 $\left(E\right)$ 入射到某一表面上，一部分 $\left(\rho E\right)$ 被反射，一部分 $\left(\alpha E\right)$ 被吸收，还有一部分 $\left(\tau E\right)$ 被透射。由于在大多数应用中，相关表面对红外光谱中的热辐射是不透明的，因此这些表面可以被视为不透明。因此，透射率可以忽略不计。由此，根据能量守恒定律，得出 $\alpha +\rho =1$，因为 $\alpha =\epsilon$（发射率），且 $\rho =1-\epsilon$。

5.3.7.2 S2S 模型方程

从给定表面离开的能量通量由直接发射的能量和反射的能量组成。反射能量通量取决于来自周围环境的入射能量通量，这可以用离开所有其他表面的能量通量来表示。从表面 $k$ 离开的能量为 $$q_{\text{out },k}={\epsilon }_k\sigma T_k^4+{\rho }_k{q}_{\text{in },k}\text{\hspace{1em}(5.131)}$$

其中，$q_{\text{out},k}$ 是离开表面的能量通量，${\epsilon }_k$ 是发射率，$\sigma$ 是斯特藩-玻尔兹曼常数，而 $q_{\text{in},k}$ 是从周围环境入射到表面的能量通量。

从一个表面到另一个表面的入射能量量是表面间“视角因子”$F_{jk}$ 的直接函数。视角因子 $F_{jk}$ 是离开表面 $j$ 的能量中入射到表面 $k$ 的部分。计算视角因子时所用的表面可以是网格面，或者是（仅限于三维情况）面的集群；关于集群的详细信息，请参见第215页的“集群与视角因子”。入射能量通量 $q_{\text{in},k}$ 可以用离开所有其他表面的能量通量来表示： $$A_k{q}_{\text{in},k}=\sum _{j=1}^N{A}_j{q}_{\text{out},j}{F}_{jk}\text{\hspace{1em}(5.132)}$$

其中，$A_k$ 是表面 $k$ 的面积，$F_{jk}$ 是表面 $k$ 和表面 $j$ 之间的视角因子。对于 $N$ 个表面，利用视角因子的互易关系可以得到： $$A_j{F}_{jk}=A_k{F}_{kj}\text{对于}j=1,2,3,\dots N\text{\hspace{1em}(5.133)}$$

因此，

$$q_{in,k}=\sum _{j=1}^N{F}_{kj}{q}_{\text{out },j}\text{\hspace{1em}(5.134)}$$

因此，

$$q_{\text{out },k}={\epsilon }_k\sigma T_k^4+{\rho }_k\sum _{j=1}^N{F}_{kj}{q}_{\text{out },j}\text{\hspace{1em}(5.135)}$$

可以写作：

$$J_k=E_k+{\rho }_k\sum _{j=1}^N{F}_{kj}{J}_j\text{\hspace{1em}(5.136)}$$

其中，$J_k$表示表面$k$发出的能量（或辐射度），而$E_k$表示表面$k$的发射功率。这表示了$N$个方程，可以重新排列成矩阵形式。

$$KJ=E\text{\hspace{1em}(5.137)}$$

其中，$K$ 是一个 $N\times N$ 的矩阵，$J$ 是辐射度向量，而 $E$ 是发射功率向量。

方程 5.137（第 215 页）被称为辐射度矩阵方程。两个有限表面 $i$ 和 $j$ 之间的视角因子由以下公式给出：

$$F_{ij}=\frac{1}{A_i}{\iint }_{A_i{A}_j}\frac{\cos {\theta }_i\cos {\theta }_j}{\pi r^2}{\delta }_{ij}d{A}_{i}d{A}_j\text{\hspace{1em}(5.138)}$$

其中，${\delta }_{ij}$ 由 $d{A}_j$ 对 $d{A}_i$ 的可视性决定。如果 $d{A}_j$ 对 $d{A}_i$ 可见，则 ${\delta }_{ij}=1$，否则为 0。

5.3.7.3 聚类

在计算大量表面的辐射和视因子时，S2S 辐射模型的计算成本非常高。为了减少计算时间和存储需求，通过创建表面“聚类”来减少表面的数量。表面聚类的生成从某个面开始，逐步添加其邻居及其邻居，直到收集到指定数量的面为止。

5.3.7.3.1 聚类和视因子

默认情况下，视因子是基于面对面计算的，其中仅有限地使用了聚类。边界面作为视因子计算的表面，然后通过取聚类内面视因子的面积加权平均值来获得聚类视因子。

对于三维情况，您可以选择使用聚类对聚类的基础来代替面与面的基础，这可以减少计算成本和存储需求。在这种方法中，Ansys Fluent 内部通过将每个聚类中非多面体单元的所有面组合来创建多边形面，并将其用作视因子计算的表面。.s2s 文件将包含聚类本身的连接信息，而不是聚类中单个面的信息，并且写入的较粗糙的多面体网格需要的磁盘空间更少。请注意，由于以下原因，使用聚类对聚类基础可能会影响准确性：

• 在计算视角因子时，假定簇是平面的，尽管它们可能并非完全平面。这种差异会降低准确性，特别是当表面变得更加凸/凹，以及边界区域的每个表面簇的面数增加时。

• 作为半立方体算法的一部分，将面分割成子面的选项（这会增加准确性）在簇到簇的基础上是不可用的。

5.3.7.3.2 簇和辐射度

辐射度 $J$ 是针对表面簇计算的。然后，这些值被分配到簇中的各个面，以计算墙体温度。由于辐射源项高度非线性（与温度的四次方成比例），必须小心计算表面簇的平均温度，并在构成簇的面之间适当分配通量和源项。

表面簇的温度通过面积平均获得，如下式所示： $$T_{sc}={\left(\frac{\sum _f{A}_f{T}_f^4}{\sum A_f}\right)}^{1/4}\text{\hspace{1em}(5.139)}$$ 其中 $T_{sc}$ 是表面簇的温度，$A_f$ 和 $T_f$ 分别是面 $f$ 的面积和温度。求和是对一个表面簇的所有面进行的。

5.3.8 蒙特卡罗（MC）辐射模型理论

蒙特卡罗辐射模型模拟了感兴趣系统的底层过程，即光子与其环境之间的物理相互作用。从光子源中选择一个光子，并跟踪它在系统中的路径，直到其权重降至某个最小值以下，此时该光子“消亡”。每当光子经历一个“事件”（例如，表面交点、散射或吸收）时，感兴趣的物理量都会更新。这个过程生成该光子在系统中的完整“历史”。为了获得系统中感兴趣物理量的良好估计，需要生成许多光子历史。光子源是根据发射辐射选择的（即“采样”），对于非灰模型，每个频带都是独立处理的。

本节提供了MC模型中使用的方程的详细信息。有关设置模型的信息，请参阅用户指南中的“设置MC模型”。

5.3.8.1 MC模型方程

对于辐射传递方程（RTE），蒙特卡罗模型假设强度与光子的微分角通量成正比，并将辐射场视为光子气体。对于这种气体，$a$ 是在给定频率下光子被吸收的概率每单位长度。因此，平均辐射强度 $I$ 与光子在单位体积 $\overrightarrow{r}$ 中单位时间内行进的距离成正比。

类似地，光谱辐射热流 $q_{in}$ 与光子在 $\overrightarrow{r}$ 处的表面入射率成正比，因为体积吸收与光子吸收率成正比。

通过跟踪典型选择的光子并在每个体积单元中记录行进距离，可以获得平均总强度。

通过跟踪典型选择的光子并在每个体积单元中计算距离乘以吸收系数，您可以获得平均总吸收强度。

通过跟踪典型选择的光子并在每个体积单元中计算距离乘以散射系数，您可以获得平均总散射强度。

同时，通过统计入射到表面的光子数量及其乘以发射率，您可以获得平均总辐射通量和平均吸收通量。

请注意，不需要对光谱进行离散化，因为对于传热计算，微分量通常并不重要。只要光谱（多波段）选择得当，蒙特卡洛统计会自动对光谱进行积分。非灰DO模型的边界条件是基于波段应用的。在波段内的处理与灰DO模型相同。

5.3.8.1.1 蒙特卡洛解的精度

蒙特卡洛辐射模型以随机方式生成光子，因此如果目标历史记录数相对较少，将产生斑点状结果。增加目标历史记录数会产生更平滑、更准确的结果，但代价是计算量更大。

5.3.8.2 MC模型的边界条件处理

边界处理与灰辐射的DO模型类似。更多详情，请参阅关于DO模型边界条件处理的章节。

注意：

不支持具有边界源和壳传导的外部壁（如果同时启用两者，则禁用壳传导）。

5.3.9 燃烧流中的辐射

5.3.9.1 灰气体加权和模型

加权灰气体总和模型（WSGGM）是在过于简化的灰气体模型和考虑特定吸收带的完整模型之间的一种合理折中。WSGGM的基本假设是，在距离$s$上的总发射率可以表示为

$$\epsilon =\sum _{i=0}^I{a}_{\epsilon ,i}\left(T\right)\left(1-e^{-{\kappa }_{i}ps}\right)\text{\hspace{1em}(5.140)}$$

其中，$a_{\epsilon ,i}$ 是第 $i^{\text{th}}$ 个虚构灰气的发射率加权因子，括号内的量是第 $i^{\text{th}}$ 个虚构灰气的发射率，${\kappa }_i$ 是第 $i^{\text{th}}$ 个灰气的吸收系数，$p$ 是所有吸收气体的分压总和，$s$ 是路径长度。对于 $a_{\epsilon ,i}$ 和 ${\kappa }_i$，Ansys Fluent 使用从 [121]（第 1064 页）和 [611]（第 1092 页）获得的值。这些值取决于气体成分，而 $a_{\epsilon ,i}$ 还取决于温度。当总压力不等于 $1\mathrm{atm}$ 时，使用 ${\kappa }_i$ 的缩放规则（参见公式 5.147（第 219 页））。

对于 $i=0$，吸收系数被赋予零值，以考虑高吸收光谱区域之间的光谱窗口（$\left(\sum _{i=1}^l{a}_{\epsilon ,i}<1\right)$），而 $i=0$ 的加权因子从 [611]（第 1092 页）评估得出： $$a_{\epsilon ,0}=1-\sum _{i=1}^I{a}_{\epsilon ,i}\text{\hspace{1em}(5.141)}$$

$a_{\epsilon ,i}$ 的温度依赖性可以用任何函数近似，但最常见的近似是 $$a_{\epsilon ,i}=\sum _{j=1}^J{b}_{\epsilon ,i,j}{T}^{j-1}\text{\hspace{1em}(5.142)}$$

其中，$b_{\epsilon ,i,j}$ 是发射率气体温度多项式系数。系数 $b_{\epsilon ,i,j}$ 和 ${\kappa }_i$ 是通过将公式 5.140（第 217 页）拟合到实验获得的总体发射率表来估计的 [121]（第 1064 页），[138]（第 1064 页），[611]（第 1092 页）。

壁面辐射的吸收率 $\alpha$ 可以采用类似方法近似计算 [611]（第1092页），但为了简化问题，我们假设 $\epsilon =\alpha$ [446]（第1083页）。除非介质光学厚度极小且壁面温度与气体温度相差较大，否则这一假设是合理的。

由于系数 $b_{\epsilon ,i,j}$ 和 ${\kappa }_i$ 是 $ps$ 和 $T$ 的缓慢变化函数，因此可以假设它们在较宽的参数范围内保持恒定。在 [611]（第1092页）中，针对不同相对压力下的 ${\mathrm{CO}}_2$ 和 ${\mathrm{H}}_2\mathrm{O}$ 蒸气，假设总压力 $p_T$ 为 $1\mathrm{atm}$，给出了这些恒定系数的值。[611]（第1092页）中显示的系数值在 $0.001\le ps\le 10.0\mathrm{atm}$ - $\mathrm{m}$ 和 $600\le T\le 2400\mathrm{K}$ 范围内有效。对于 $T>2400\mathrm{K}$，使用 [121]（第1064页）建议的系数值。如果对所有 $i$ 都有 ${\kappa }_{i}ps\ll 1$，则方程 5.140（第217页）简化为 $$\epsilon =\sum _{i=0}^I{a}_{\epsilon ,i}{\kappa }_{i}ps\text{\hspace{1em}(5.143)}$$

将方程 5.143（第218页）与吸收系数为 $a$ 的灰体模型进行比较，可以看出在 WSGGM 中，辐射强度在距离 $s$ 上的变化与吸收系数为 $$a=\sum _{i=0}^I{a}_{\epsilon ,i}{\kappa }_{i}p\text{\hspace{1em}(5.144)}$$ 的灰体模型完全相同，且该系数不依赖于 $s$。在一般情况下，$a$ 的估计值为 $$a=-\frac{\ln \left(1-\epsilon \right)}{S}\text{\hspace{1em}(5.145)}$$

在Ansys Fluent中，WSGGM的发射率$\epsilon$是根据公式5.140（第217页）计算的。定义中的$a$（公式5.145，第218页）取决于$s$，反映了分子气体中热辐射吸收的非灰性质。在Ansys Fluent中，当$s\le {10}^{-4}\mathrm{m}$时使用公式5.144（第218页），而对于$s>{10}^{-4}\mathrm{m}$的情况，则使用公式5.145（第218页）。需要注意的是，当$s\approx {10}^{-4}\mathrm{m}$时，公式5.144（第218页）和公式5.145（第218页）预测的$a$值实际上是相同的（因为在小$s$的极限情况下，公式5.145（第218页）简化为公式5.144（第218页））。

Ansys Fluent允许你将$s$设置为平均光束长度。你可以指定平均光束长度，或者让Ansys Fluent根据Siegel [596]（第1091页）的以下公式计算： $$s=3.6\frac{V}{A}\text{\hspace{1em}(5.146)}$$ 其中$V$是流体体积，$A$是流体边界（壁面、入口、出口；不包括对称面）的总表面积。

有关为WSGGM设置属性的详细信息，请参阅用户指南中的“Inputs for a Composition-Dependent Absorption Coefficient”部分。

重要提示：WSGGM是在灰度方法中实现的。如果将WSGGM与非灰度模型一起使用，吸收系数将在所有波段中相同。使用DEFINE_GRAY_BAND_ABS_COEFF可以按波段或按灰度气体更改吸收系数。

5.3.9.1.1 当总（静态）气体压力不等于1 atm时

如上所述，WSGGM假设总（静态）气体压力$p_{tot}$等于1 atm。在$p_{\text{tot}}$不等于1的情况下（例如，高温燃烧），根据[158]（第1066页）中提出的缩放规则进行修正。当$p_{tot}<0.9\mathrm{atm}$或$p_{\text{tot }}>1.1\mathrm{atm}$时，方程5.140（第217页）和方程5.144（第218页）中的${\kappa }_i$值会重新缩放： $${\kappa }_i\to {\kappa }_i{p}_{\text{tot }}^m\text{\hspace{1em}(5.147)}$$ 其中$m$是一个无量纲值，来源于[158]（第1066页），取决于吸收气体的分压和温度$T$，以及$p_{\text{tot}}$。

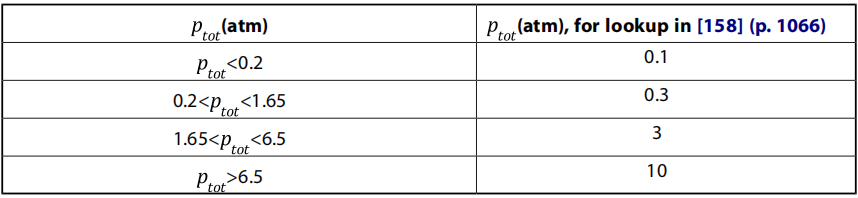
需要注意的是，压力缩放指数$m$是根据$p_{\text{tot}}$确定的，具体如下：

表5.1：压力修正因子查找值

5.3.9.2 煤烟对吸收系数的影响

当计算煤烟形成时，Ansys Fluent可以考虑煤烟浓度对辐射吸收系数的影响。广义煤烟模型通过确定煤烟的有效吸收系数来估计煤烟对辐射传热的影响。煤烟和吸收（辐射）气体混合物的吸收系数则计算为纯气体和纯煤烟吸收系数的总和： $$a_{s+g}=a_g+a_s\text{\hspace{1em}(5.148)}$$

其中，$a_g$ 是无烟气体的吸收系数（从 WSGGM 获得）， $$a_s=b_1{\rho }_g{Y}_{\text{soot }}\left[1+b_T\left(T-2000\right)\right]\text{\hspace{1em}(5.149)}$$

其中 $$b_1=1232.4{\mathrm{m}}^2/\mathrm{kg}$$ 和 $$b_T\approx 4.8\times {10}^{-4}{\mathrm{K}}^{-1}$$

${\rho }_g$ 是气体混合密度，单位为 $kg/m^3$，$Y_{\text{soot }}$ 是烟尘质量分数。

系数 $b_1$ 和 $b_T$ 是通过拟合公式 5.149（第 220 页）得到的，数据基于 Taylor-Foster 近似 [648]（第 1094 页）和基于 Smith 等人近似 [611]（第 1092 页）的数据 [572]（第 1090 页）。

有关包含烟尘辐射相互作用效应的信息，请参阅用户指南中的辐射属性及使用烟尘模型部分。

5.3.9.3 颗粒对吸收系数的影响

Ansys Fluent 还可以包括离散相颗粒对辐射吸收系数的影响，前提是您使用的是 P-1 或 DO 模型。当 P-1 或 DO 模型处于活动状态时，可以启用颗粒的辐射吸收。然后，颗粒的发射率、反射率和散射效应将包含在辐射传热计算中。有关离散相辐射属性输入的更多详细信息，请参阅用户指南中的设置离散相材料属性部分。

5.3.10 选择辐射模型

对于某些问题，某个辐射模型可能比其他模型更合适。在决定使用哪个辐射模型时，请考虑以下因素：

• 光学厚度：光学厚度 $aL$ 是判断在你的问题中应使用哪种模型的一个良好指标。这里，$L$ 是你问题域的一个适当长度尺度。例如，对于燃烧室内的流动，$L$ 是燃烧室的直径。如果 $aL\gg 1$，你最好的选择是 P-1 和 Rosseland 模型。通常情况下，P-1 模型应用于光学厚度 $>1$ 的情况。对于光学厚度 $>3$，Rosseland 模型更经济高效。对于高光学厚度的情况，建议为 DO 模型使用二阶离散化方案。DTRM、DO 和 MC 模型适用于全范围的光学厚度，但使用成本显著更高。因此，如果问题允许，应使用“厚极限”模型，即 P-1 和 Rosseland。对于光学薄的问题（$aL$ <1），仅 DTRM、DO 和 MC 模型适用。

• 散射和发射率：P-1、Rosseland 和 DO 模型考虑了散射，而 DTRM 则忽略了它。由于 Rosseland 模型在壁面使用温度滑移条件，因此对壁面发射率不敏感。

• 颗粒效应：只有 P-1 和 DO 模型考虑了气体与颗粒之间的辐射交换（参见公式 5.68（第 191 页））。

• 半透明壁（内部和外部）：DO 和 MC 模型允许你模拟各种类型的半透明壁（例如，玻璃）。MC 模型确实允许在耦合壁的情况下使用半透明边界条件。

• 镜面壁：DO 和 MC 模型允许镜面反射（例如，无尘镜）。

• 部分镜面壁：DO 和 MC 模型允许部分镜面反射（例如，有尘镜）。

• 非灰体辐射：只有 P-1、DO 和 MC 模型允许您使用灰带模型计算非灰体辐射。

• 局部热源：在存在局部热源的问题中，P-1 模型可能会过高估计辐射通量。DO 模型可能最适合计算此类情况的辐射，尽管具有足够多射线的 DTRM 也是可以接受的。

• 非参与介质中的封闭辐射传递：表面到表面（S2S）模型适用于此类问题。原则上，与参与介质一起使用的辐射模型也可以用于计算表面到表面辐射，但它们并不总是高效的。

5.3.10.1 外部辐射

如果您需要考虑物理模型外部的辐射热传递，可以在模型中包含外部辐射边界条件（详细信息请参阅用户指南中的“墙壁上的热边界条件”）。如果您不关心域内的辐射，可以在不激活任何辐射模型的情况下使用此边界条件。