ANSYS FLUENT使用基于控制体积的技术(有限体积法)将一般标量输运方程转换为可进行数值求解的代数方程。这种方法包括对每个控制体积内的输运方程进行积分,得到离散的代数方程,该方程在控制体积的基础上表达守恒定律。
以标量的瞬态输运方程为例说明控制方程的离散化。对于任意控制体,以积分形式写成下面的形式: 式中,为密度;为速度向量;为面积向量;为扩散系数;为的梯度;为单位体积的的源项。
公式(1)被应用到计算域中的每个控制体上(如下图所示)以得到离散方程。
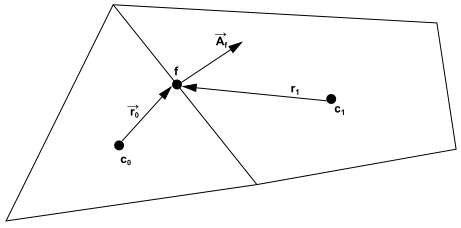
离散方程为: 式中,为封闭网格单元的面数;为通过面的对流量;为网格面的面积向量;为网格面上变量的梯度;为网格体积。
23.2.1 求解线性系统
离散的标量输运方程(式2)包含网格中心处的未知标量变量以及周围相邻网格中的未知值。一般来说,这个方程关于这些变量是非线性的。式2的线性化形式可以写为: 式中,下标表示相邻的网格;及分别为及的线性系数。
每个网格的相邻网格数量取决于网格拓扑,但通常等于包围网格的面数(边界网格除外)。
可以为将计算区域中的每个网格写入类似的方程。这形成了一组具有稀疏系数矩阵的代数方程组。对于标量方程, Fluent使用点隐式(Gauss-Seidel)线性方程求解器和代数多重网格(AMG)方法来求解此线性系统。