多参考系中的流动

涉及多个运动部件的问题无法采用单参考系方法进行模拟。对于这类问题，必须将模型分解为多个流体/固体单元区域，各区域之间由界面边界分隔。包含运动组件的区域可使用运动参考系方程（运动参考系的方程 (第21页)）求解，而静止区域则可采用静止坐标系方程求解。在Fluent中，处理这些界面处方程的方式支持两种方法：

多运动参考系
- 多参考系模型（MRF）（参见《多参考系模型》第24页）
- 混合平面模型（MPM）（参见《混合平面模型》第28页）
滑移网格模型（SMM）

MRF和混合平面方法均为稳态近似，主要区别在于界面条件的处理方式。这些方法将在下文中讨论。而滑移网格模型方法则由于网格随时间运动的特性，本质上是不稳定的。该方法在《使用滑动和动态网格的流动》第35页中讨论。

MRF模型[399]（第1080页）可能是处理多区域问题的两种方法中最简单的一种。它是一种稳态近似，其中各个单元区域可以被赋予不同的旋转和/或平移速度。每个运动单元区域的流动通过运动参考系方程求解。（详细内容请参见“运动参考系中的流动”（第21页））。如果该区域是静止的 $(ω = 0)$ ，方程简化为静止形式。在单元区域之间的界面处，执行局部参考系变换，以便使用一个区域的流动变量来计算相邻区域边界处的通量。MRF界面公式的具体讨论将在“MRF界面公式”（第26页）中进行更详细的阐述。

需要注意的是，MRF方法并未考虑运动区域相对于相邻区域（可能也在运动或静止）的相对运动；计算时网格保持固定。这类似于将运动部件的运动冻结在特定位置，并观察该位置下的瞬时流场。因此，MRF常被称为“冻结转子法”。

尽管MRF方法显然是一种近似处理，但它能为许多应用提供合理的流动模型。例如，在涡轮机械应用中，当转子和定子之间的相互作用较弱且流动在运动与静止区域的交界处相对简单时，可以使用MRF模型。在搅拌槽中，由于叶轮与挡板间的相互作用较弱，不存在大规模瞬态效应，因此也可以采用MRF模型进行模拟。

MRF模型的另一个潜在应用是计算流场，该流场可作为瞬态滑移网格计算的初始条件。这样就无需进行启动计算。然而，如果需要实际模拟强转子-定子相互作用中可能出现的瞬态现象，则不应使用多参考系模型，而应仅使用滑移网格模型（参见用户指南中的“使用滑动和动态网格模拟流动”部分）。

2.3.1.2. 示例

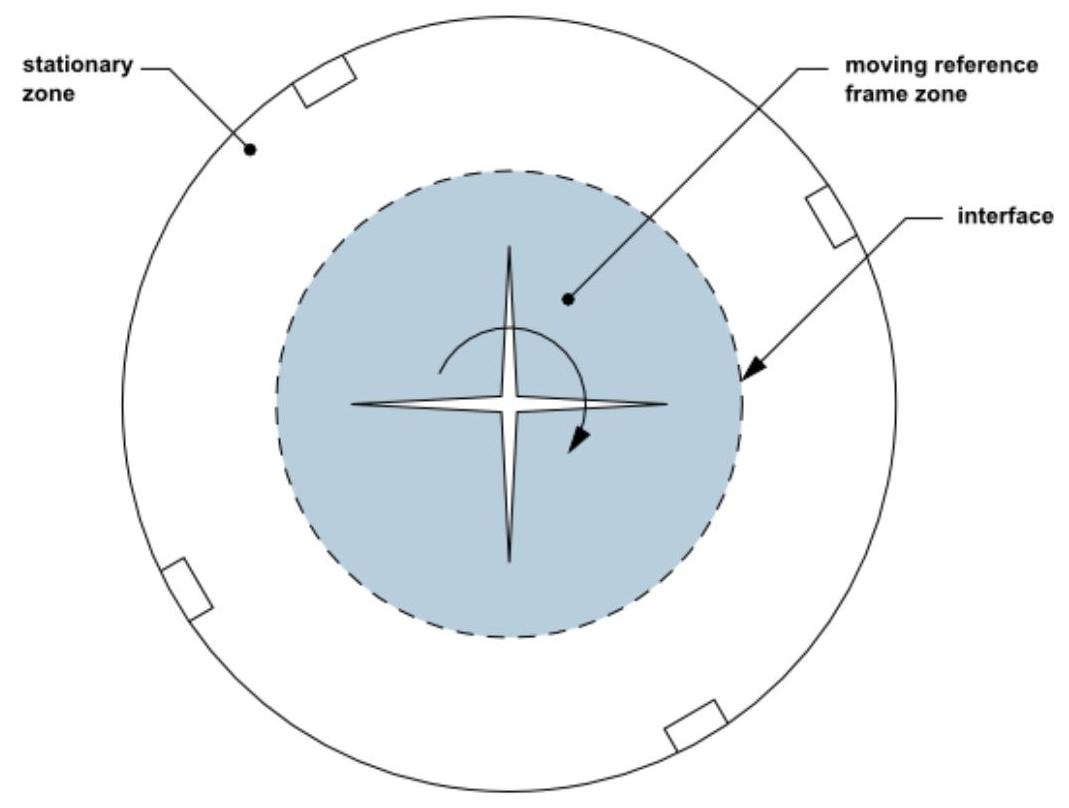
对于配备单个叶轮的混合罐，可以定义一个运动参考系来包含叶轮及其周围的流动，同时对叶轮区域外的流动使用固定参考系。图2.4展示了这种配置的示例：带有单个旋转叶轮的几何结构（第25页）。（虚线表示两个参考系之间的界面。）假设在两个参考系的界面处为稳态流动条件，即界面上每个参考系的速度必须相同（以绝对值表示）。网格不运动。

图2.4：带有单个旋转叶轮的几何结构

您还可以构建一个包含多个运动参考系的问题模型。图2.5：带有两个旋转叶轮的几何结构（第26页）展示了一个包含两个并排旋转叶轮的几何体。此问题将采用三个参考系进行模拟：固定在两个叶轮区域外部的静止参考系，以及分别为两个叶轮设定的两个独立运动参考系。（如前所述，虚线表示各参考系之间的界面。）

图2.5：带有两个旋转叶轮的几何结构

2.3.1.3 MRF交界面公式

应用于交界面（Interface）的MRF公式取决于所使用的速度公式。针对每种情况的具体方法将在下文讨论。需要注意的是，交界面处理适用于速度和速度梯度，因为这些矢量随参考系的改变而变化。标量如温度、压力、密度、湍流动能等，不需要特殊处理，因此可以在本地直接传递而不做任何更改。

注意：Fluent 使用的界面公式未考虑不同法向（相对于界面）的单元区域速度。您应指定相邻两个单元区域的运动方式，使得界面法向速度差为零。

2.3.1.3.1. 界面处理：相对速度公式

在Fluent的MRF模型实现中，计算域被划分为多个子域，每个子域可能相对于实验室（惯性）坐标系进行旋转和/或平移。每个子域中的控制方程是相对于该子域的参考系书写的。因此，静止和运动子域中的流动由连续性和动量方程（第2页）控制，而运动子域中的流动则由运动参考系的方程（第21页）控制。

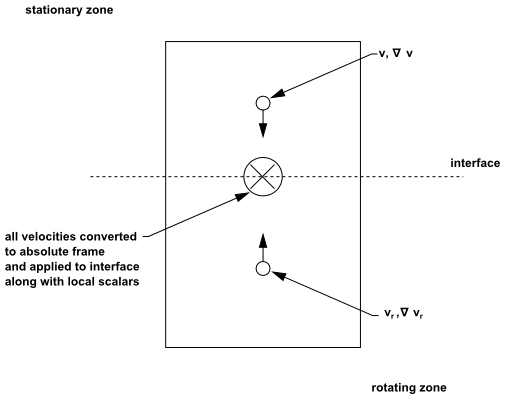
在两个子域的交界处，一个子域中控制方程的扩散项及其他项需要相邻子域的速度值（参见图2.6：MRF模型的界面处理（第27页））。Fluent强制绝对速度 $v$ 的连续性，以确保所考虑子域正确获取相邻子域的速度值。（这种方法与混合平面模型中所述的方法不同（第28页），后者采用周向平均技术。）

当采用相对速度公式时，每个子域内的速度是相对于该子域的运动计算的。通过方程2.15（第27页）将速度和速度梯度从运动参考系转换到绝对惯性系。

图2.6：MRF模型的界面处理

对于一个平移速度 $v_{t}$ ，我们有

$v = v_{r} + (ω \times r) + v_{t} (2.15)$

从公式2.15（第27页）可以看出，绝对速度矢量的梯度可以表示为

$\nabla v = \nabla v_{r} + \nabla (ω \times r) (2.16)$

请注意，像密度、静压、静温、组分质量分数等标量数据，都是直接从相邻单元格中局部获取的。

2.3.1.3.2. 界面处理：绝对速度公式

使用绝对速度公式时，每个子域的控制方程是相对于该子域的参考系书写的，但速度存储在绝对坐标系中。因此，两个子域之间的界面不需要特殊变换。同样，标量值从相邻单元局部确定。

2.3.2 混合平面模型

在Fluent中，混合平面模型（Mixing Plane Model）为模拟具有一个或多个相对运动区域的流场提供了一种替代多参考系模型和滑移网格模型的方法。本节简要概述了该模型及其局限性列表。

2.3.2.1. 概述

如《多重参考系模型》（第24页）中所讨论的，当相邻运动/静止区域界面处的流动近乎均匀（“混合完毕”）时，MRF模型适用。如果该界面处的流动不均匀，MRF模型可能无法提供物理上有意义的解决方案。在这种情况下，滑移网格模型（参见用户指南中的“使用滑动和动态网格模拟流动”）可能是合适的，但在许多情况下采用滑移网格并不实际。例如，在多级涡轮机械中，如果每排叶片数量不同，则需要大量叶片通道以保持周向周期性。此外，滑移网格计算必然是不稳定的，因此为了达到最终的时间周期性解需要显著更多的计算资源。对于那些不适合使用滑移网格模型的情形，混合平面模型可以作为一种经济有效的替代方案。

在混合平面方法中，每个流体区域被视为稳态问题。来自相邻区域的流动场数据作为边界条件传递，这些条件在混合平面接口处进行空间平均或“混合”处理。这种混合消除了由于通道间流动场的周向变化（例如尾迹、激波、分离流）引起的任何非定常性，从而得到一个稳态结果。尽管混合平面模型存在固有的简化，但其得到的解仍能提供时间平均流动场的合理近似。

2.3.2.2 转子和定子域

考虑图2.7（轴向转子-定子相互作用示意图，展示混合平面概念）（第29页）和图2.8（径向转子-定子相互作用示意图，展示混合平面概念）（第29页）所示的涡轮机械级。每个叶片通道包含周期性边界。图2.7展示了轴流式机器中单级的恒定径向平面，而图2.8则显示了混流设备中的恒定 $θ$ 平面。在每种情况下，该级由两个流动域组成：旋转于规定角速度的转子域，随后是静止的定子域。转子和定子的顺序是任意的（即，转子位于定子下游的情况同样有效）。

图2.7：轴向转子-定子相互作用（示意图展示混合平面概念）

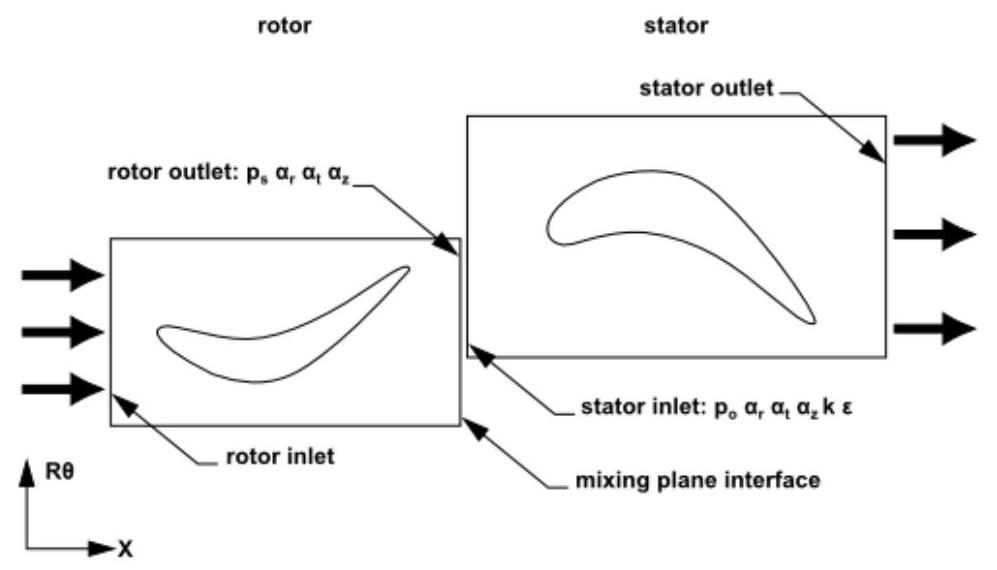
图2.8：径向转子-定子相互作用（示意图展示混合面概念）

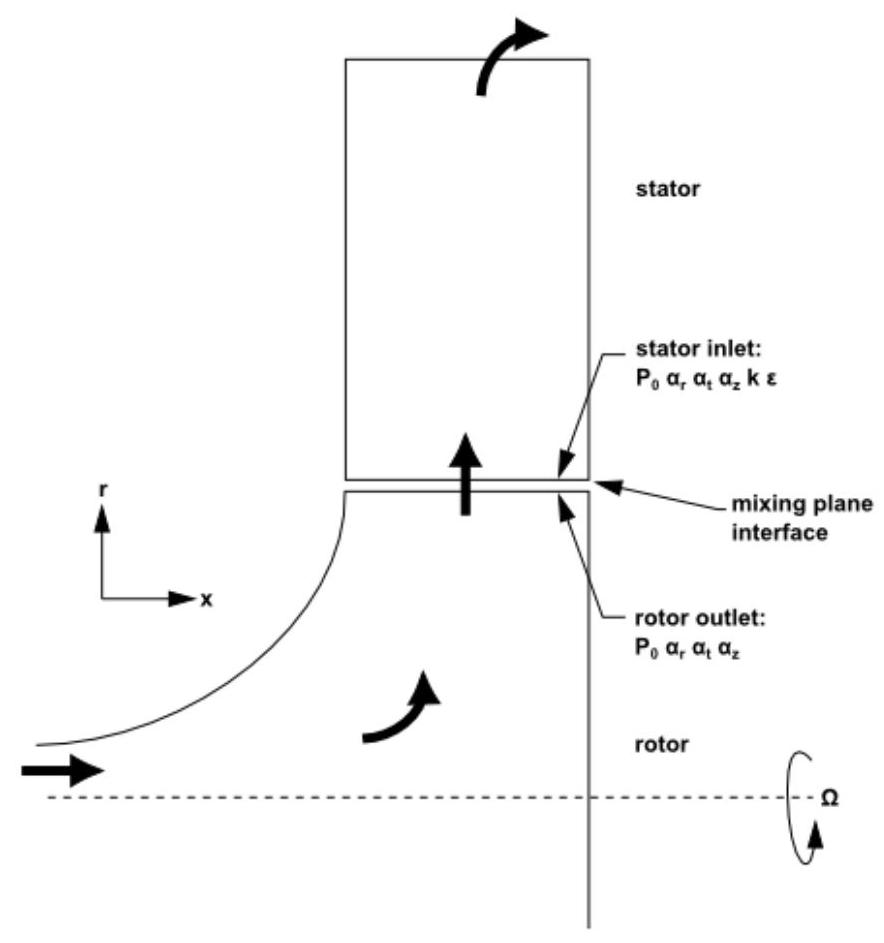
在数值模拟中，每个区域将由一个独立的网格表示。这些区域之间的流动信息将在混合平面接口处耦合（如图2.7：轴向转子-定子相互作用（说明混合平面概念的示意图）（第29页）和图2.8：径向转子-定子相互作用（说明混合平面概念的示意图）（第29页）所示），使用混合平面模型实现。请注意，您可以这种方式耦合任意数量的流体区域；例如，四个叶片通道可以通过三个混合平面进行耦合。

重要提示：请注意，定子和转子通道是独立的单元区域，各自具有自己的入口和出口边界。您可以将此系统视为一组为每个叶片通道设置的SRF模型，通过混合平面模型提供的边界条件进行耦合。

2.3.2.3. 混合平面概念

混合平面概念的核心思想是将每个流体区域视为稳态问题进行求解。在规定的迭代间隔内，混合平面接口处的流动数据会在静子出口和转子入口边界上沿周向进行平均处理。Fluent提供了三种平均方法供选择：面积加权平均、质量平均和混合输出平均。通过在指定的径向或轴向位置执行周向平均，可以定义边界条件流动变量的“轮廓”。这些轮廓——根据混合平面的方向，可能是轴向或径向坐标的函数——随后用于更新混合平面接口两侧区域的边界条件。如图2.7所示的轴向转子-静子相互作用（示意图展示混合平面概念）（第29页）和图2.8所示的径向转子-静子相互作用（示意图展示混合平面概念）（第29页）中，计算了转子出口处的总压 $(p_{0})$ 、径向、切向和轴向上当地流动角的方向余弦 $(α_{r}, α_{t}, α_{z})$ 、总温 $(T_{0})$ 、湍流动能 $(k)$ 以及湍流耗散率 $(ε)$ 的平均值轮廓，并据此更新静子入口的边界条件。同样地，计算了静子入口处的静压 $(p_{s})$ 及相应方向余弦后作为转子出口的边界条件使用。

如上所述，在混合面接口传递轮廓的前提是已在该接口定义了特定的边界条件类型。将上游出口边界区域与下游入口边界区域相耦合的操作称为“混合面配对”。要在Fluent中创建混合面配对，边界区域必须属于以下类型：

Upstream	Downstream
pressure outlet	pressure inlet
pressure outlet	velocity inlet
pressure outlet	mass-flow inlet

关于设置混合平面的具体指导，请参阅用户指南中的“设置传统混合平面模型”部分。

2.3.2.4. 选择平均方法

在混合平面模型中提供了三种轮廓平均方法：

面积平均法
质量平均法
混合输出平均法

2.3.2.4.1. 区域平均法

区域平均法是默认的平均方法，其定义如下：

$\overset{ˉ}{f} = \frac{1}{A} \int_{A} fd A (2.17)$

重要提示：通过面积平均获得的压力和温度可能无法准确代表流体的动量和能量。

2.3.2.4.2. 质量加权平均

质量加权平均的计算公式为

$\overset{ˉ}{f} = \frac{1}{m ˙} \int_{A} f ρ V \cdot n d A (2.18)$

其中

$\overset{m}{˙} = \int_{A} ρ V \cdot n d A (2.19)$

此方法相较于面积平均法能更好地反映总量。若混合平面存在严重逆流，可能会引发收敛问题。因此，为了保证解的稳定性，建议先采用面积平均启动计算，待逆流消失后再切换至质量平均。

重要提示：多相流中无法使用质量平均。

2.3.2.4.3. 混合输出平均法

混合输出平均法基于质量、动量和能量的守恒原理推导而来：

$F = \int_{A} ρ (V \cdot \overset{n}{^}) d A M_{1} = \int_{A} ρ (V \cdot \overset{n}{^}) u d A + \int_{A} P (\overset{e}{^}_{x} \cdot \overset{n}{^}) d A M_{2} = \int_{A} ρ (V \cdot \overset{n}{^}) v d A + \int_{A} P (\overset{e}{^}_{y} \cdot \overset{n}{^}) d A M_{3} = \int_{A} ρ (V \cdot \overset{n}{^}) w d A + \int_{A} P (\overset{e}{^}_{z} \cdot \overset{n}{^}) d A E = \frac{γ R}{( γ - 1 )} \int_{A} ρ (V \cdot \overset{n}{^}) T d A + \frac{1}{2} \int_{A} ρ (V \cdot \overset{n}{^}) (u^{2} + v^{2} + w^{2}) d A (2.20)$ 由于基于守恒原则，混合平均被认为能更好地代表流动情况，因为它反映了与流动轮廓不均匀性相关的损失。然而，与质量加权平均法类似，当混合平面存在严重逆流时，可能会出现收敛困难。因此，最佳做法是先采用面积平均启动求解过程，待逆流消失后再切换到混合平均。

混合平均假设流体为具有常数定压比热的可压缩理想气体 $C_{p}$ 。

重要提示：多相流情况下无法使用混合平均方法。

2.3.2.5. Fluent混合平面算法

Fluent的基本混合平面算法可以描述如下：

更新静子和转子域中的流场解。
在静子出口和转子入口边界处平均流体属性，获取用于更新边界条件的轮廓。
将这些轮廓传递到静子出口和转子入口所需的边界条件输入中。
重复步骤1-3直至收敛。

重要提示：注意，为了防止解的发散（尤其是在计算初期），可能需要对边界条件值的变化进行欠松弛处理。Fluent允许您控制混合平面变量的欠松弛程度。

2.3.2.6. 质量守恒

需要注意的是，如果混合平面由压力出口和压力入口对表示，上述算法不会严格保持通过混合平面的质量流量守恒。相反，如果你使用压力出口和质量流量入口对，Fluent将强制实现混合平面上的质量守恒。基本技术包括计算上游区域（压力出口）的质量流量，并调整应用于质量流量入口的质量通量分布，使得下游的质量流量与上游匹配。这种调整在每次迭代中都会进行，从而确保在整个计算过程中严格保持质量流量的守恒。

重要提示：请注意，由于在这种情况下固定了质量流量，因此混合平面上的总压会有跳跃。与流场其他地方的总压变化相比，这种跳跃的幅度通常较小。

2.3.2.7. 旋流守恒

默认情况下，Fluent在混合平面处不保持旋流守恒。对于扭矩转换器等应用，作用在组件上的扭矩总和应为零，因此在混合平面处强制执行旋流守恒至关重要，这在Fluent中作为模拟选项提供。确保旋流守恒很重要，因为否则会在混合平面接口处存在切向动量的源或汇。

考虑一个包含静止或运动部件（例如泵叶轮或涡轮叶片）的控制体积。利用流体力学中的动量矩方程可以证明，对于稳态流动，

$T = \iint_{S} r v_{θ} ρ v \cdot n d S (2.21)$

其中， $T$ 表示流体作用在部件上的扭矩， $r$ 是从旋转轴到径向的距离， $v_{θ}$ 是绝对切向速度， $v$ 是总的绝对速度，而 $S$ 是边界表面。（乘积 $r v_{θ}$ 被称为旋度。）

对于一个具有明确进出口边界的周向周期性域，方程2.21（第33页）变为

$T = \int \int_{outlet} r v_{θ} ρ v \cdot n d S + \int \int_{inlet} r v_{θ} ρ v \cdot n d S (2.22)$

其中，“inlet”和“outlet”分别表示进口和出口边界表面。

现在考虑混合平面接口具有有限的轴向厚度。将方程2.22（第33页）应用于该区域，并注意到在厚度收缩至零的极限情况下，扭矩应消失，方程变为：

$\int downstream \int r v_{θ} ρ v \cdot n d S = \int upstream \int r v_{θ} ρ v \cdot n d S (2.23)$

上游和下游分别指混合面接口的上游侧和下游侧。需要注意的是，公式2.23（第33页）适用于混合面接口的全区域（360度）。

公式2.23（第33页）提供了一种合理的方法来确定切向速度分量。即，Fluent计算出一个切向速度分布图，然后均匀调整该分布以满足旋流积分条件。需要注意的是，在混合面上插值切向（及径向）速度分量分布不会影响质量守恒，因为这些速度分量与用于计算质量通量的面向法线速度正交。

2.3.2.8.总焓守恒

默认情况下，Fluent在混合平面处不保持总焓守恒。对于某些应用，混合平面处的总焓守恒非常理想，因为效率等全局参数直接与叶片排或级间的总焓变化相关。这在Fluent中作为模拟选项提供。

确保总焓守恒的过程简单地涉及调整下游总温分布，使得积分后的总焓与上游积分后的总焓相匹配。对于多相流，质量、旋流和焓的守恒针对每个相进行计算。然而，对于欧拉多相模型，由于不允许质量流量入口，上述量的守恒不会发生。

2.3.1.多参考系模型

2.3.1.1.概述