对于选定的表面,您可以计算并报告等熵效率和多变效率的值。有关支持的表面和可用于效率计算的工具的信息,请参阅《Fluent用户指南》中的效率计算部分。有关Ansys Fluent如何计算效率值的信息,请参阅以下部分:
- 25.5.1. 等熵效率
- 25.5.2. 多变效率
25.5.1 等熵效率
由于流体动力学和热力学在整个系统中的损失,任何设备的效率都不可能是完美的。这些损失表现为实际值与如果过程完全等熵时预期值之间的差异。考虑图25.2所示的T-s图上绘制的过程:压缩和膨胀过程的T-s图(第1049页)。
图25.2:压缩和膨胀过程的T-s图
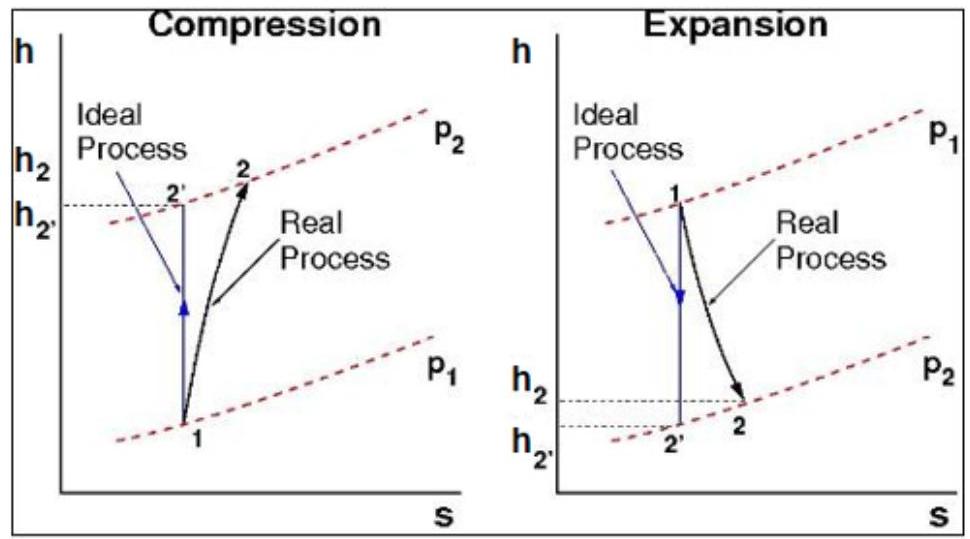
对于任一过程,有三种效率计算选项:总至总、总至静态和静态至静态。
对于膨胀过程(例如,在蒸汽涡轮机中),这些选项由以下比率定义:
其中, 和 分别是点1和点2处的总焓的质量平均值,而 是点2处静焓的质量平均值。此外,还需要等熵总焓 和等熵静焓 。它们根据状态方程进行评估:
在压缩过程中(例如在气体压缩机中),比率方程25.40(第1049页)、方程25.41(第1049页)和方程25.42(第1049页)被反转并表述为:
其中,熵 默认取点1处的质量平均值, 是点2处静压的面积平均值,而 是点2处总压的质量流量平均值。
总到总和总到静态选项对于那些对流体做功(例如,泵或压缩机)或从流体中提取功(例如,涡轮机)的设备最为有用。静态到静态选项则适用于评估那些不对流体做功的设备(例如,扩散器和喷嘴)中的损失。
25.5.2 多变效率
等熵效率有一个显著的缺点,即无法将流体动力学损失与总损失(流体动力学 + 热力学)分开。这意味着即使流体动力学质量相似,具有不同压力比的设备也会有不同的等熵效率。例如,两个压力比不同的压缩机,高压比压缩机由于热力学损失会有较低的等熵效率。这一特性可能使得比较不同压缩机设计变得困难。类似的论点也适用于涡轮机设计。
为了克服这一缺点,过程所假设的“理想”路径不必是等熵的。相反,可以通过沿着恒定效率线来评估多变效率。Aungier [31](第1058页)讨论了如何在T-s图上通过以下方程近似表示恒定效率路径:
这个方程可以重新排列,得到以下两个关系式:
沿此路径的熵变通过积分最后一个表达式来评估:
重新整理这个表达式,我们便能得出沿指定路径的常数A的值:
要评估多变效率,需沿由路径方程定义的替代路径计算多变焓变。我们从第二定律开始:
项代表多变功或焓变,这是我们需要求解的内容。首先,我们利用公式 25.49(第 1050 页)来替换 项,得到:
沿着多方路径对这一方程进行积分,得到:
多变焓可以通过简单地省略减去 来从多变焓变化 中获得。此外,代入 A 可以得到多变总焓 的最终形式:
多变静焓 是通过将点 2 处的总参数替换为静态参数来评估的:
在公式25.40(第1049页)至25.42(第1049页)以及公式25.45(第1050页)至25.47(第1050页)中,使用和替代和,即可评估相应的多变效率值。