本节介绍裂隙模型的理论基础。相关信息可在以下章节中找到：

10.3.1. 概述

10.3.2. 局限性

10.3.3. 裂隙模型理论

有关使用裂隙模型的信息，请参阅用户指南中的“使用裂隙模型”部分。

10.3.1. 概述

Ansys Fluent 中实现的裂隙模型是一种基于 Namazian 和 Heywood [470]（第 1084 页）以及 Roberts 和 Matthews [558]（第 1089 页）提出的模型的零维环流模型。该模型主要针对缸内特定流动，更具体地说，是直喷式（DI）柴油发动机，因此仅适用于时间相关的模拟。

该模型从相邻两个边界的单元中获取质量、动量和能量，并考虑活塞裂隙体积中的质量储存。使用裂隙模型需要详细的环和活塞几何信息，通常是围绕发动机缸径的环包。图 10.3：裂隙模型几何（活塞）（第 428 页）至图 10.5：裂隙模型“网络”表示（第 428 页）展示了一个示例表示。

图 10.3：裂隙模型几何（活塞）

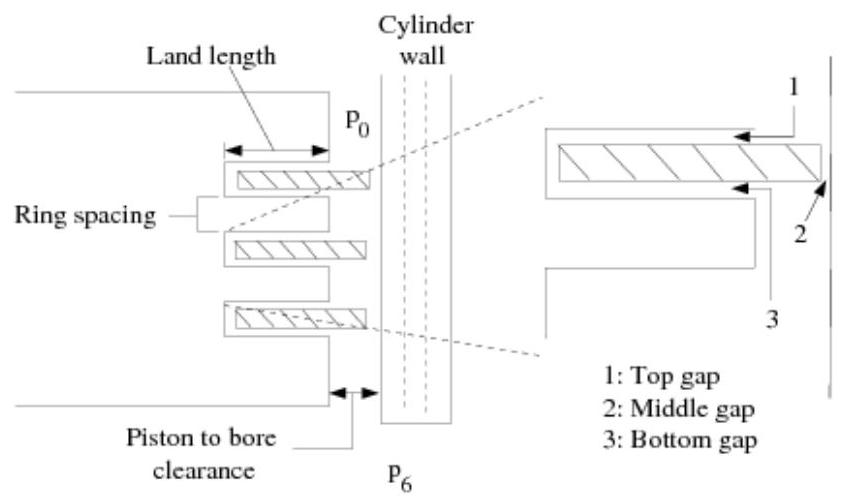
图 10.4：裂隙模型几何（环）

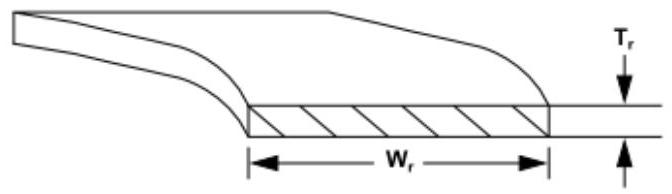
图 10.5：裂隙模型“网络”表示

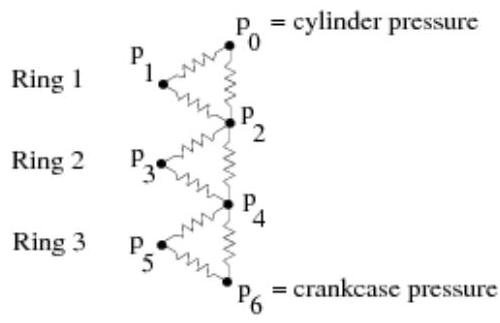
10.3.1.1. 模型参数

• 活塞与缸径间隙是指活塞与缸径之间的距离。典型值在火花点火发动机（SI）中为 2 至 5 密尔（80 至 120 微米），在某些柴油发动机（DI）中为 4 至 7 密尔（100 至 240 微米）。

• 环厚度是图 10.4：裂隙模型几何（环）（第 428 页）中的变量 $T_r$。典型值在 SI 发动机中为 1 至 3 毫米，在 DI 发动机中为 2 至 4 毫米。

• 环宽是指图10.4中裂隙模型几何（环）（第428页）中的变量$W_r$。对于$\mathrm{SI}$发动机，典型值范围为3至$3.5\mathrm{mm}$，而对于$\mathrm{DI}$柴油发动机，则为4至$6\mathrm{mm}$。

• 环间距是指一个环槽底部与下一个环槽顶部之间的距离。对于$\mathrm{SI}$发动机，环间距的典型值为3至$5\mathrm{mm}$，而对于$\mathrm{DI}$柴油发动机，则为4至$8\mathrm{mm}$。

• 环槽长度是指环槽的深度（即活塞上的切口）；总是比环的宽度深约$1\mathrm{mm}$。对于$\mathrm{SI}$发动机，典型值为4至$4.5\mathrm{mm}$，而对于DI柴油发动机，则为5至$7\mathrm{mm}$。

• 顶部间隙是指环槽与环顶部之间的间隙（40至$80\mu \mathrm{m}$）。

• 中部间隙是指环与缸孔之间的距离（10至$40\mu \mathrm{m}$）。

• 底部间隙是指环槽与环底部之间的间隙（40至$80\mu \mathrm{m}$）。

• 共享边界和泄漏壁是指大多数缸内模拟中的活塞（例如，wall-8）和气缸壁（例如，wa11.1）。与活塞顶部和气缸壁共享边界的单元格被定义为裂隙单元格。

环带组是密封活塞在气缸孔内的那组环。当阀门关闭时（例如，在四冲程循环发动机的压缩冲程期间），活塞在气缸内向上移动，气缸内的压力升高，流动开始通过环。环带组中的压力分布是通过假设完全发展的可压缩流通过环与活塞之间的空间，或者环与气缸壁之间的阻塞可压缩流来建模的。

由于环带组中的温度是固定的且几何形状已知，一旦计算出压力分布，就可以使用理想气体状态方程找到每个体积中的质量。在Ansys Fluent解决方案的每个离散步骤中，也计算了环带组总体质量流出的量（即，通过指定最后一个环的流动）。

10.3.2. 限制

缝隙模型的限制在于它是零维的、瞬态的，并且目前仅限于共享边界的两个线程。

使用零维方法是因为难以准确预测缝隙中组分的横向扩散。如果在模拟中组分的横向扩散很重要，例如当直喷发动机中的喷雾羽流靠近边界且净质量流进入缝隙时，建议在Ansys Fluent中使用非共形网格模拟完整的多维缝隙几何。此外，这种方法不具体追踪个别组分，因为任何个别组分都会立即分布在整个环带组中。从缝隙进入域的质量流被假定具有与质量流入的单元相同的组成。

裂隙流动方程的制定本质上是非定常的，并使用Ansys Fluent的刚性方程求解器进行求解。对于存在泄漏流动的稳态问题，可以通过将瞬态问题运行至稳态来解决。当前裂隙模型的额外限制在于仅允许单一裂隙存在，并且仅有一条线可以发生泄漏。虽然可以在模拟过程中设定活塞环位置，但并未显式考虑活塞环的动态特性。

在这种情况下，裂隙模型求解是一个刚性的初值边界问题。随着活塞环裂隙间压力差增大以及整个活塞环组压力差增大，刚性也随之增加。因此，如果时间步长开始时初始条件与解相距甚远，常微分方程（ODE）求解器可能无法成功积分这些方程。解决此问题的一种方法是减小流动时间步长进行多次迭代。另一种解决方案是使用更接近于时间步长结束时解的初始条件开始计算。

10.3.3. 裂隙模型理论

Ansys Fluent通过假设活塞与活塞环上下表面之间为层流可压缩流动，以及假设活塞环与气缸壁之间为孔口流动，来求解裂隙几何形状中的质量守恒方程。通过活塞环端隙的质量流方程形式如下：

$${\dot{m}}_{ij}=C_d{A}_{ij}\rho c{\eta }_{ij}\text{\hspace{1em}(10.13)}$$

其中，$C_d$ 是流量系数，$A_{ij}$ 是间隙面积，$\rho$ 是气体密度，$c$ 是当地声速，而 ${\eta }_{ij}$ 是一个由以下公式给出的压缩因子。

$${\eta }_{ij}=\{\begin{array}{cc}\frac{2}{\gamma -1}{\left[{\left(\frac{p_i}{p_j}\right)}^{\frac{2}{\gamma }}-{\left(\frac{p_i}{p_j}\right)}^{\frac{2}{\gamma }}\right]}^{0.5}& \frac{p_i}{p_j}>0.52\\ {\left(\frac{2}{\gamma -1}\right)}^{\frac{\gamma +1}{2\left(\gamma -1\right)}}& \frac{p_i}{p_j}\le 0.52\end{array}\text{\hspace{1em}(10.14)}$$

其中，$\gamma$ 是比热比，$p_i$ 是上游压力，$p_j$ 是下游压力。通过活塞环顶部和底部面（即进入和离开活塞环后方体积）的质量流量的方程式为：

$${\dot{m}}_{ij}=\frac{h_{ij}^2\left(p_i^2-p_j^2\right)A_{ij}}{24W_r{\mu }_{gas}RT}\text{\hspace{1em}(10.15)}$$

其中，$h_{ij}$ 表示间隙的横截面积，$W_r$ 是气体流动环的宽度，${\mu }_{\text{gas }}$ 为局部气体粘度，$T$ 是气体温度，$R$ 为普适气体常数。针对一组三个环的方程系统形式如下：

$$\frac{d{p}_{{}_1}}{dt}=\frac{p_{{}_1}}{m_1}\left({\dot{m}}_{01}-{\dot{m}}_{12}\right)\text{\hspace{1em}(10.16)}$$

$$\frac{d{p}_2}{dt}=\frac{p_2}{m_2}\left({\dot{m}}_{02}+{\dot{m}}_{12}-{\dot{m}}_{23}-{\dot{m}}_{24}\right)\text{\hspace{1em}(10.17)}$$

$$\frac{d{p}_3}{dt}=\frac{p_3}{m_3}\left({\dot{m}}_{23}-{\dot{m}}_{34}\right)\text{\hspace{1em}(10.18)}$$

$$\frac{d{p}_{{}_4}}{dt}=\frac{p_{{}_4}}{m_4}\left({\dot{m}}_{24}+{\dot{m}}_{34}-{\dot{m}}_{45}-{\dot{m}}_{46}\right)\text{\hspace{1em}(10.19)}$$

$$\frac{d{p}_{{}_5}}{dt}=\frac{p_{{}_5}}{m_5}\left({\dot{m}}_{45}-{\dot{m}}_{56}\right)\text{\hspace{1em}(10.20)}$$

其中，$p_0$ 表示缝隙单元内的平均压力，而 $p_6$ 则是从文本界面输入的曲轴箱压力。对于数值上相邻的区域（例如，0-1、1-2、2-3等），其质量流量的表达式由方程10.15（第430页）给出；而对于间隔两个整数的区域（例如，$0-2,2-4,4-6$），其质量流量的表达式则由方程10.13（第430页）和方程10.14（第430页）提供。因此，为了求解环组方程，需要 $2n_r-1$ 个方程，其中 $n_r$ 代表模拟中环的数量。