壁面-颗粒反弹模型理论

对于非旋转粒子，Ansys Fluent 提供了一个模型，该模型考虑了由于与壁面发生非弹性碰撞而导致的能量损失。粒子根据恢复系数定义，在与相关边界碰撞后，其动量发生变化并反弹离开壁面。（参见图12.2：壁面处的粒子反射（第492页）。）

图12.2 壁面处的粒子反射

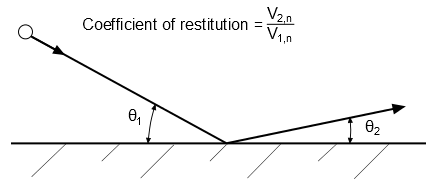
法向恢复系数定义了粒子在与边界碰撞后，在垂直于壁面方向上保留的动量大小[642]：

$e_{n} = \frac{V _{2, n}}{V _{1, n}} (12.193)$

其中， $V_{n}$ 表示粒子垂直于壁面的速度，下标 1 和 2 分别表示碰撞前和碰撞后的状态。类似地，切向恢复系数 $e_{t}$ 定义了粒子在沿壁面切线方向上保留的动量。

对于旋转粒子，Ansys Fluent 提供了一个模型，用于估算粒子从壁面反弹后的速度，该模型由 Tsuji 等人提出 [660]（第 1095 页）。该模型基于经典力学（参见图 12.3：粒子-壁面碰撞力），并考虑了由于非弹性碰撞和摩擦引起的能量损失。

图 12.3 粒子-壁面碰撞力

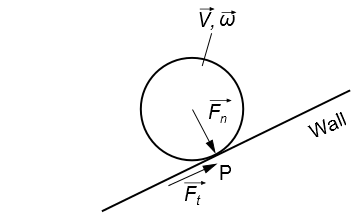
在此模型中，粒子和壁面接触的时间被分为两个阶段：压缩阶段和恢复阶段。方程系统根据粒子是否在压缩阶段内停止滑动来定义。

粘附碰撞

如果在压缩阶段内粒子停止滑动，则以下条件成立：

$F_{t} \leq μ F_{n} (12.194)$

方程 (12.194)（第 493 页）中相等的极限情况对应于库仑摩擦定律（方程 (12.505)（第 580 页）），其中切向力 $F_{t}$ 与法向力 $F_{n}$ 成正比，比例系数为摩擦系数 $μ$ 。

粒子在与墙壁碰撞前后的动量方程如下：

$m_{p} (V_{n} - V_{n}^{0}) m_{p} (V_{t} - V_{t}^{0}) I_{p} (ω_{n} - ω_{n}^{0}) I_{p} (ω_{t} - ω_{t}^{0}) = - J_{n} = - J_{t} = M_{n} = M_{t} = - r \times J_{t} (12.195)$

其中，

$m_{p}$ 和 $I_{p}$ 分别代表粒子的质量和转动惯量（后者假设粒子为球形）。

$M$ 是相对于质心的扭矩。

$V$ 和 $ω$ 分别表示粒子的线速度和角速度。

$J$ 是动量。

$r$ 是粒子的半径。

上标 0 表示粒子在与墙碰撞前的速度。

下标 $n$ 和 $t$ 分别表示变量的法向和切向分量。

恢复系数 $e_{n}$ 定义为碰撞前后法向动量之比。如果粒子在反弹过程中质量保持不变，恢复系数可以简化为碰撞前后粒子法向速度之比：

$e_{n} = \frac{J _{n}}{J _{n}^{0}} = - \frac{V _{n}}{V _{n}^{0}} (12.196)$

碰撞过程中，壁面法向的角动量不受影响，即 $M_{n} = 0$ 。这导致了粒子角速度的静态（不变）特性：

$ω_{n} = ω_{n}^{0} (12.197)$

对于粘附性冲击，可以定义以下在粒子与壁面接触点的速度边界条件：

$V_{t}^{p} = V_{t} + r \times ω_{t} = 0 (12.198)$

其中上标 $p$ 表示碰撞过程中接触点的颗粒速度（参见图 12.3：颗粒-壁面碰撞力（第 493 页））。

对于给定的边界条件，可以通过求解方程 12.195（第 493 页）来计算碰撞后的速度 $V$ 和 $ω$ 。

滑动冲击

如果切向力超过摩擦力（即方程 12.194（第 493 页）中的不等式不成立），颗粒在压缩期间不会停止滑动。颗粒的线速度和角速度在运动学上不相关，碰撞后的速度可以直接从各自的动力学方程中估算。方程 12.196（第 494 页）和方程 12.197（第 494 页）仍然有效。切向动量的变化可以使用方程 12.194（第 493 页）定义如下：

$m_{p} (V_{t} - V_{t}^{0}) = \int_{t 1}^{t 0} F_{t} d t = \int_{t 1}^{t 0} - μ F_{n} ε_{t} d t (12.199)$

其中，

$ε_{t} = sign (V_{t}) (12.200)$

其中，sign 是符号函数，对于正值返回 +1，对于负值返回 -1。注意：

当启用粒子旋转时，切向恢复系数（壁面边界条件对话框的 DPM 标签）不被考虑。粒子从壁面反弹后的切向线速度是粒子碰撞前线速度 $V$ 和角速度 $ω$ 的函数。

有关如何使用粒子旋转模型的信息，请参阅 Fluent 用户指南中的 Particle Rotation。

12.7.1 粗糙壁面模型

粗糙壁面模型可以更真实地捕捉分散流在受限几何体中的行为，例如旋风分离器和管道系统。关于粒子-壁面相互作用的研究表明，大颗粒或重颗粒的运动受表面粗糙度的强烈影响。

Ansys Fluent 中使用的粗糙壁面模型基于 [617]（第 1092 页）和 [189]（第 1067 页）中的理论发现。在粒子-壁面碰撞的时刻，壁面被替换为在粒子-壁面接触点处与虚拟粗糙壁面相切的表面。

图 12.4：粗糙壁面上的粒子-壁面相互作用

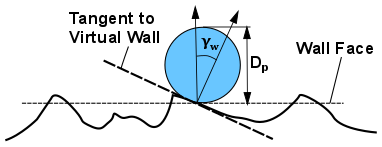
倾斜角 $γ_{w}$ （即壁面法向量与虚拟壁面相切表面的法向量之间的角度），是根据统计表面粗糙度参数和当前粒子直径计算得出的。

图 12.5：壁面粗糙度参数（第 495 页）说明了如何估计表面粗糙度参数。有关工业中使用的统计表面粗糙度参数的详细信息，请参阅 ISO 4287。

图 12.5：壁面粗糙度参数

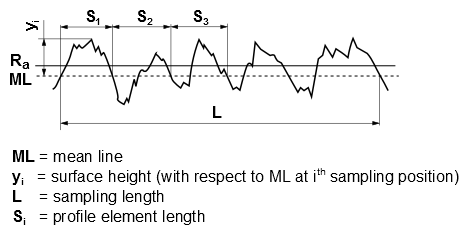
ML = 平均线

$y_{i} =$ 表面高度（相对于第 $i^{th}$ 采样位置的 ML）

$L =$ 采样长度

壁面粗糙度参数如下：

壁面平均粗糙度 $R_{a}$ :

$R_{a} = \frac{1}{L} \int_{0}^{L} ∣ y (x) ∣ d x$

粗糙度结构 $R_{q}$ 的标准差：

$R_{q} = \frac{1}{L} \int_{0}^{L} y^{2} (x) d x$

采样长度内平均轮廓元素宽度/间距 $R S_{m}$ ：

$R S_{m} = \frac{1}{p} i = 1 \sum p S_{i}$

其中， $p$ 表示在采样长度 $L$ 内的轮廓元素数量。

倾斜角 $γ_{w}$ 从均值为 $0^{\circ}$ 、标准差为 $Δ γ$ 的高斯分布中采样得到。

高斯分布的虚拟墙角标准差估计如下：

$Δ γ = {arctan (2 R_{q} / R S_{m}) arctan (2 R_{a} / R S_{m}) if D_{p} < \frac{R S _{m}}{s i n ( a r c t a n ( 2 R _{a} / R S _{m} ) )} otherwise (12.201)$

其中，

$Δ γ =$ 高斯分布虚拟墙角度的标准差

$D_{p} = particle diameter$

该模型考虑了“阴影效应”[617]（第1092页），即如果粒子速度矢量（碰撞前）与虚拟墙法向矢量之间的角度大于 $π /2$ 弧度，粒子无法与虚拟墙发生物理碰撞。

一旦通过其法向矢量定义了新的虚拟墙，就使用公式12.193（第492页）至公式 $12.200$ （第494页）来计算反射粒子相对于虚拟墙的反弹速度。