本节内容由以下部分组成:
- 14.4.1 概述
- 14.4.2 混合模型的局限性
- 14.4.3 连续性方程
- 14.4.4 动量方程
- 14.4.4 动量方程
- 14.4.5 能量方程
- 14.4.6 相对(滑移)速度与漂移速度
- 14.4.7 次要相的体积分数方程
- 14.4.8 颗粒属性
- 14.4.9 颗粒温度
- 14.4.9 颗粒温度
- 14.4.10 固体压力
- 14.4.11 界面面积浓度
- 14.4.12 流动状态建模
14.4.1 概述
混合模型是一种简化的多相模型,可用于多种方式。它可以用于模拟各相以不同速度移动的多相流,但假设在短的空间长度尺度上局部平衡。它也可以用于模拟具有强烈耦合且各相以相同速度移动的均质多相流。
混合模型可以通过求解混合物的动量、连续性和能量方程,次要相的体积分数方程以及相对速度的代数表达式来模拟 相(流体或颗粒)。典型应用包括沉降、旋风分离器、低载荷的颗粒负载流动以及气体体积分数保持较低的气泡流动。
在几种情况下,混合模型是完整欧拉多相模型的良好替代品。当存在颗粒相的广泛分布或相间定律未知或其可靠性可质疑时,完整的多相模型可能不切实际。像混合模型这样的简化模型可以在解决比完整多相模型更少的变量的情况下表现得与完整多相模型一样好。
混合模型允许您选择颗粒相并计算所有颗粒相的性质。这适用于液固流动。
14.4.2 混合模型的局限性
Ansys Fluent 中的混合模型具有以下局限性:
-
必须使用基于压力的求解器。混合模型在基于密度的求解器中不可用。
-
当使用混合模型时,不要模拟具有指定质量流率的流向周期性流动。
-
不要在混合模型中同时模拟固化和熔化过程。
-
不要将相对公式与MRF(多参考系)和混合模型结合使用(参见用户指南中的限制)。
-
混合模型不允许无粘流动。
-
当结合混合模型使用DPM(离散相模型)跟踪颗粒时,不能选择共享内存方法(离散相模型的并行处理)。(请注意,使用消息传递或混合方法可以使所有多相流模型与DPM模型兼容。)
混合模型与VOF模型类似,都采用单一流体方法。它在两个方面与VOF模型不同:
-
混合模型允许各相相互渗透。因此,控制体积的体积分数和可以在0到1之间取任意值,具体取决于相和相所占据的空间。
-
混合模型允许各相以不同速度移动,使用滑移速度的概念。(请注意,也可以假设各相以相同速度移动,此时混合模型简化为一个均质多相模型。)
-
混合模型与非预混、部分预混和预混燃烧模型不兼容。
混合模型解决了混合物的连续性方程、混合物的动量方程、混合物的能量方程以及次要相的体积分数方程,还包括相对速度的代数表达式(如果各相以不同速度运动)。
14.4.3 连续性方程
混合物的连续性方程为
其中, 表示质量平均速度:
以及 是混合物的密度:
表示相 的体积分数。
14.4.4 动量方程
混合物的动量方程可以通过将所有相的单独动量方程相加得到。它可以表示为
其中, 表示相的数量, 是体力, 是混合物的粘度:
是次相 的漂移速度:
14.4.5 能量方程
混合物的能量方程具有以下形式:
其中, 表示相 中物种 的焓, 表示相 中物种 的扩散通量,而 则是通过以下方式计算的有效导热系数:
其中,是根据所使用的湍流模型定义的湍流热导率。
方程14.125(第643页)右侧的前三项分别表示由于传导、物种扩散和粘性耗散引起的能量传递。最后一项包括您定义的体积热源,但不包括由有限速率体积或表面反应产生的热源,因为如“反应引起的能量源”(第174页)所述,物种生成焓已经包含在总焓计算中。
在方程14.125中,
对于可压缩相,,而对于不可压缩相,,其中是相的显焓。
14.4.6 相对(滑移)速度与漂移速度
相对速度(也称为滑移速度)定义为次相相对于主相的速度:
任意相(记作)的质量分数定义如下:
漂移速度与相对速度之间通过以下表达式相联系:
其中 表示相 相对于相 的速度。
Ansys Fluent 的混合模型采用了代数滑移公式。代数滑移混合模型的基本假设是,为了规定相对速度的代数关系,应在短的空间长度尺度上达到相之间的局部平衡。根据 Manninen 等人 [411](第 1080 页),相对速度的形式如下:
其中, 表示颗粒松弛时间。
表示次相 的粒子(或液滴或气泡)的直径, 是次相粒子的加速度。默认的曳力函数 取自 Schiller 和 Naumann [577](第 1090 页):
加速度 的形式为
最简单的代数滑移公式是所谓的漂移通量模型,其中颗粒的加速度由重力和/或离心力给出,并且颗粒松弛时间被修改以考虑其他颗粒的存在。
在湍流流动中,相对速度应包含由于分散相动量方程中出现的分散而产生的扩散项。Ansys Fluent将这种分散添加到相对速度中:
其中, 是一个设定为0.75的普朗特/施密特数,而 是湍流扩散系数。该扩散系数根据连续分散的脉动速度相关性计算得出。
其中, 表示受交叉轨迹效应影响的能量湍流涡流时间尺度与颗粒松弛时间之间的时间比率,,而 。
在解决具有滑移速度的混合多相计算时,您可以直接规定阻力函数的公式。以下选项可供选择:
-
Schiller-Naumann(默认公式) -
Morsi-Alexander -
symmetric -
Grace et al. -
Tomiyama et al. -
universal drag laws -
constant -
user-defined
有关这些阻力函数及其公式的更多信息,请参阅《相间交换系数》(第667页),以及《用户指南》中关于如何启用它们的说明。
请注意,如果未解决滑移速度,混合模型将简化为均质多相模型。此外,混合模型可以通过用户定义的函数进行定制,以使用除代数滑移方法之外的公式来计算滑移速度。详情请参阅《Fluent定制手册》。
14.4.7 次要相的体积分数方程
从次要相 的连续性方程中,可以得到次要相 的体积分数方程:
14.4.8 颗粒属性
由于颗粒浓度是计算混合物有效粘度的重要因素,我们可以利用颗粒粘度来获取悬浮液的粘度值。体积加权平均的粘度现在将包含由于颗粒平移和碰撞引起的动量交换产生的剪切粘度。
碰撞部分和动能部分,以及可选的摩擦部分,被加总以得到固体剪切粘度:
参见固体压力(第694页)以了解用于颗粒流动中的常数定义。
14.4.8.1. 碰撞粘度
剪切粘度的碰撞部分被建模为[205](第1068页),[640](第1094页)。
14.4.8.2 动力粘度
Ansys Fluent 提供了两种动力粘度的表达式。
默认的表达式来自 Syamlal 等人 [640](第 1094 页):
以下可选表达式来自Gidaspow等人[205](第1068页),亦可供使用:
14.4.9 颗粒温度
黏度需要指定第 种固体相的颗粒温度。在此,我们采用颗粒温度输运方程的代数形式。这仅适用于稠密流化床,前提是颗粒能量的产生与耗散处于平衡状态,可以忽略对流项和扩散项。
哪里
碰撞能量耗散率表示由于颗粒间碰撞,在第种固体相中能量耗散的速率。此项由Lun等人[397](第1080页)推导的表达式表示。
颗粒速度随机波动动能从第固体相向第流体或固体相的传递,由 [205] (第1068页)表示:
Ansys Fluent 提供了以下选项来求解颗粒温度:
代数形式(默认选项)
这是通过忽略传输方程(公式14.143,第646页)[640](第1094页)中的对流和扩散得到的。
恒定颗粒温度
这在非常密集的情况下非常有用,此时随机波动很小。
颗粒温度UDF
14.4.10 固体压力
总非过滤固体压力被计算并包含在混合物动量方程中:
其中, 在颗粒流部分的公式 14.349(第 695 页)中给出。
14.4.11 界面面积浓度
界面面积浓度定义为两相之间单位混合体积的界面面积。这是预测通过相间界面的质量、动量和能量传递的重要参数。当使用带有非颗粒次相的混合多相模型时,你可以让 Ansys Fluent 通过以下方式之一计算界面面积:
-
使用界面面积浓度的输运方程,如输运方程模型(第 647 页)中所述。这允许气泡直径的分布以及聚并/破裂效应。
-
使用一个指定的气泡直径与界面面积密度之间的代数关系。更多信息请参见代数模型(第 651 页)。
基于输运方程的界面面积浓度(IAC)模型(输运方程模型(第 647 页))和代数模型(代数模型(第 651 页))之间的主要区别在于,代数模型假设界面是球形的,而 IAC 模型可以通过求解一个输运方程直接预测界面面积浓度。
14.4.11.1 基于输运方程的模型
在两相流系统中,一个是离散的(颗粒),另一个是连续的,离散相或颗粒的大小及其分布会由于生长(相间质量传递)、压力变化引起的膨胀、聚并、破裂和/或成核机制而迅速改变。人口平衡模型(见人口平衡模型(第 783 页))理想地捕捉了这一现象,但由于需要使用矩方法或更多(如果使用离散方法)求解几个输运方程,计算成本较高。界面面积浓度模型针对当前阶段的液体中的气泡流,每个次相使用一个输运方程。
界面面积浓度输运方程可以表述为:
其中, 是界面面积浓度 , 是气体体积分数。方程 14.147(第 647 页)右侧的前两项表示由于可压缩性和质量传递(相变)导致的气泡膨胀。 是每单位混合体积进入气相的质量传递速率 。 和 分别是由于随机碰撞和尾流卷吸引起的聚并汇项。 是由于湍流冲击引起的破碎源项。
对于界面面积浓度的这些源项和汇项,存在两组模型,即 Hibiki-Ishii 模型 [244](第 1071 页)和 Ishii-Kim 模型 [306](第 1075 页),[272](第 1072 页),这些模型基于 Ishii 等人的工作 [244](第 1071 页),[306](第 1075 页)。根据他们的研究,相互作用的机制可以总结为五个类别:
- 由于湍流驱动的随机碰撞引起的聚并。
- 由于湍流涡流冲击引起的破碎。
- 由于尾流卷吸引起的聚并。
- 从大帽泡上剥离小气泡。
- 由于气泡表面流动不稳定引起的大帽泡破碎。
在 Ansys Fluent 中,只考虑前三种效应。
14.4.11.1.1. Hibiki-Ishii 模型
其中,、 和 分别代表颗粒/气泡碰撞频率、碰撞后的聚并效率以及单位混合物体积内的颗粒数量。颗粒/气泡的平均尺寸 假设按以下方式计算:
以及
其中,、 和 分别表示初级相颗粒/气泡与湍流涡旋之间的碰撞频率、冲击导致的破碎效率以及单位混合体积内的湍流涡旋数量。在公式14.151(第648页)中,
实验可调系数如下所示:
请注意,基于实验数据,Ansys Fluent使用的值与Hibiki和Ishii [244](第1071页)提出的不同。如果您希望针对您的案例修改此值,请联系Ansys技术支持以了解如何自定义您的设置。
形状因子对于球形颗粒/气泡设定为6,而为。在Hibiki-Ishii公式中,没有针对的模型。
14.4.11.1.2. Ishii-Kim模型
(14.153)
其中,平均气泡波动速度 由 给出。气泡终端速度 是气泡直径和局部时间平均空隙率的函数。
其中, 表示流体相的分子粘度, 代表重力加速度, 则是界面张力。在该模型中,当韦伯数 小于临界韦伯数 时,破碎率等于零,即 。所使用的系数如下所示 [272](第1072页):
重要提示:目前,该模型仅适用于两相流动状态,其中一相为气体,另一相为液体,即适用于鼓泡塔应用。然而,您始终可以使用 UDF(用户定义函数)来包含您自己的相界面积浓度模型,这些模型可以应用于其他流动状态。
详细信息请参阅 Fluent 定制手册。
14.4.11.1.3 Yao-Morel 模型
体积相界面积是在计算相间交换力(如动量、质量和热量传递)时出现的重要量。在 Ansys Fluent 中,已经实现了 Hibiki 和 Ishii 模型([244](第 1071 页))以及 Ishii 和 Kim 模型(Hibiki-Ishii 模型(第 648 页)),用于具有整体质量传递的鼓泡流。这些模型的扩展存在。这将包括基于 Yao 和 Morel [722](第 1099 页)在核沸腾应用方面的工作,对壁面异质质量传递效果的建模。体积相界面积输运方程 14.147(第 647 页)包含一个成核项以及聚结和破碎模型。Yao 和 Morel [722](第 1099 页)将聚结项建模如下:
其中,和分别表示气泡自由移动时间和合并作用时间,为气泡数密度,为合并效率,因子1/2则是为了避免在相同气泡对之间重复计数。上述方程的最终表达式为:
其中, 为临界韦伯数,系数取值为 、、, 代表韦伯数, 是从 k-epsilon 湍流模型中获得的耗散率, 是一个修正因子,定义为 ,而 是堆积极限。关于公式 14.147(第 647 页),由于随机碰撞和尾流卷吸引起的聚并沉降项如下:
断裂项,如Yao和Morel [722](第1099页)所建模的,是
其中, 和 分别表示断裂的自由行进时间和相互作用时间, 则为断裂效率。上述方程的最终表达形式为:
此处,系数取值为 和 。
关于公式 14.147(第 647 页),由于湍流冲击引起的 破碎源项形式为
在考虑受热壁面处泡核沸腾引起的源项时,应在方程14.147(第647页)中加入一个新项。该项的形式为:
其中, 表示成核气泡的直径, 表示成核点密度, 表示气泡频率。这些参数可以与壁面沸腾模型中描述的沸腾模型相联系,详见《壁面沸腾模型》(第733页)。气泡脱离频率由公式14.514(第735页)给出,成核点密度由公式14.515(第735页)给出,而气泡脱离直径则由公式14.518(第736页)、公式14.519(第736页)或公式14.520(第736页)给出。
如需了解如何应用此模型,请参阅用户指南中“通过输运方程定义界面面积浓度”部分。
14.4.11.2 代数模型
代数模型源自球形气泡或液滴的表面积与体积比,即 :
其中, 表示气泡或液滴的直径。尽管代数模型基于气泡或液滴呈球形的假设推导得出,但在输运方程模型中,界面面积密度 的单位与 相同。当使用非颗粒次相的混合多相流模型时,您可以让 Ansys Fluent 通过以下方式之一计算界面面积:
- 对称模型(默认)
对称模型对相 和相 进行对称处理。相 和相 可以是连续相或分散相。相间面积密度计算如下:
其中, 和 分别表示相 和相 的体积分数,而 则是通过以下方式计算的特征长度尺度:
- 如果相 是分散相:
- 如果两个相态 和 都处于分散状态:
- 粒子模型
对于具有体积分数 的分散相 ,粒子模型估计界面面积密度 为
- 梯度模型
梯度模型与对称模型不同之处在于,它将相界面处的梯度作为界面长度尺度引入。该模型通常用于自由表面问题。在Ansys Fluent中,提供了两种版本的梯度模型:
- 纯梯度模型
若连续相和分散相之间存在自由表面,则界面面积密度计算如下:
对于具有两个以上相的分散-分散系统,相 和相 的界面面积密度表示为:
- 梯度对称模型
梯度对称模型根据自由表面位置计算界面面积密度,具体如下。如果 指定限制(默认值为1e-6),则使用对称模型方程14.167(第651页)计算界面面积密度。否则,界面面积密度设为零。
- 用户自定义
请参阅 Fluent 定制手册中的 DEFINE_EXCHANGE_PROPERTY。
14.4.12 流动状态建模
虽然代数滑移模型仅支持低斯托克斯数范围内的微小界面,但广义流动状态框架通过特殊的数值方法有效地处理了小规模和大规模界面以及状态转换。这对于涉及多种流动状态的多相应用的准确模拟非常重要,例如自由表面流动、泡状流动和液滴流动。有关如何使用流动状态建模的更多信息,请参阅 Fluent 用户指南中的使用流动状态建模部分。
广义流动状态框架区分三种不同的流动状态(即泡状流动、液滴流动和自由表面流动),并具有以下显著特点:
-
根据相态形态和相态状态定义流动状态。
-
基于流动状态检测标准的混合形态指定。
-
支持多个连续相和分散相。
-
针对不同相对形态的不同方法和默认设置。
-
通过代数界面面积密度(AIAD)方法以及平滑和滤波技术进行状态检测。
-
能够使用用户定义函数进行流动状态建模。
-
基于流动状态的体积分数离散化。
在流动状态建模中,表示流体连通性的相态形态分为以下几类:
- 连续
如果相态在流动域中占据一个连通区域,则该相态形态被归类为连续的。
- 分散
如果某一相态在流动域中占据不连续的区域,则该相态的形态被归类为分散态。
- 混合态
混合态形态是一种动态形态,可以根据流动状态检测标准表现为连续态或分散态。
当以下情况发生时,可以观察到混合态相态形态:
-
相态形态在空间和/或时间上变化,但没有真正的流动状态转变。
-
在气泡流、液滴流和自由表面流之间存在状态转变。
图14.7:无状态转变的混合态相态形态(第654页)展示了一个两相流的例子,其中空气呈现混合态形态,而水呈现连续态形态。在流体域中没有发生状态转变。
图14.7:无状态转变的混合态相态形态
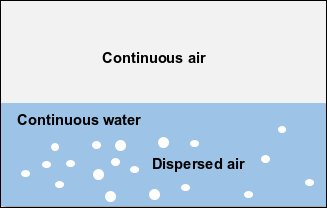
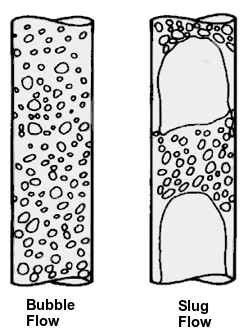
图14.8:有状态转变的混合态相态形态(第654页)展示了一个两相流中状态转变的例子,其中空气表现为混合态,而水可以表现为连续态或混合态。流动状态可能在气泡流和柱塞流之间转变。
图14.8:有状态转变的混合态相态形态
无论是相态(液体或气体)还是相态形态(连续态或分散态),对于完全定义流动状态(如自由表面流、气泡流和液滴流)都是至关重要的。
表14.2:流动状态定义(第654页)展示了基于相态形态和相态状态的不同流动状态的可能定义。
表14.2:流动状态定义
| 流动状态分类 | 相态形态 + 相态状态 |
|---|---|
| 自由表面流 | 连续液体/连续液体 连续液体/连续气体 |
| 泡状流 | 连续液体/分散气体 |
| 液滴流 | 连续气体/分散液体 连续液体/分散液体 |
14.4.12.1 混合形态的相对相互作用
对于具有相索引 和 的一对相,可能存在以下相对相互作用:
- 混合-混合
- 连续-混合
- 混合-分散
每种相对相互作用的详细信息如下所示。
- 混合-混合相对相互作用
混合-混合相对可能的相互作用如下图所示。
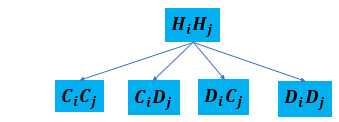
此处, 连续状态, 分散状态, 混合状态。
在上图中,
是两种相均表现为连续状态的相互作用(如自由表面流的情况)。这种相互作用将进一步称为 。
是相 表现为连续状态,相 表现为分散状态的相互作用(如泡状流或液滴流,取决于相态状态)。这种相互作用将进一步称为 。
表示的是相 作为分散相,相 作为连续相的相互作用(例如在液滴流或气泡流中,具体取决于相的状态)。这种相互作用将进一步简称为 。
表示的是两相均作为分散相的相互作用(例如在颗粒-颗粒相互作用中,这种情况仅可能发生在多于两相的流动中)。这种相互作用将进一步简称为 。
根据流动状态检测标准,计算混合因子以识别满足以下约束条件的各种流动状态:
其中, 为混合因子,下标代表如上所述的不同流动状态。
随后,面积密度可按如下方式进行混合:
其中, 表示自由表面流动的面积密度, 和 分别表示泡沫流动和液滴流动的面积密度,而 表示颗粒-颗粒流动的面积密度。
对于采用混合-混合相对的代数滑移速度模型,滑移速度的一般形式可以表示为:
对于连续-连续相的相互作用,通过施加零阻力来迫使相 和相 的速度相等,即 ,这相当于存在无限大的阻力。
对于分散-分散相的相互作用,
对于连续-分散或分散-连续相互作用,滑移速度由方程14.131(第644页)和方程14.135(第644页)指定。
- 连续-混合相对相互作用
当相 为连续相,相 为混合相时,可能的连续-混合相对相互作用如下图所示。
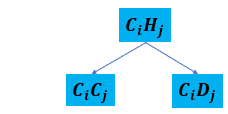
在这种情况下,,且 。
- 混合-分散相对相互作用
当相 为混合相,相 为分散相时,可能的连续-分散相对相互作用如下图所示。
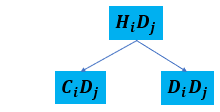
在这种情况下, 且 。
14.4.12.2 流动模式混合的代数界面面积密度方法
Ansys Fluent 使用了由 Thomas Höhne 等人 [254](第1071页)提出的代数界面面积密度方法的自定义变体来进行流动模式检测。在该方法中,使用了多种余弦函数来计算流动模式检测的混合因子。
对于相 和相 的一对相,权重函数 和 基于体积分数定义如下:
其中:
在上述方程中:
和 分别表示相 和相 的体积分数
和 分别表示相 和相 的临界体积分数。默认值:0.3
中间过渡区域的体积分数宽度。默认值:0.05 。
图 14.9:权重函数 和 (第 658 页)(改编自 [254](第 1071 页))展示了权重函数 和 随体积分数变化的图表。
图 14.9:权重函数 和
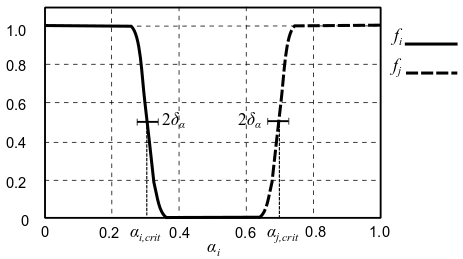
基于体积分数梯度的相边界权重函数 表示为:
其中:
在公式14.183(第658页)中, 是用于定义中间过渡宽度的临界梯度的一部分(默认值:0.1)。
在公式14.182(第658页)中, 是用于确定自由表面流动界面宽度的单元编号,而 则表示为单元尺寸:
图14.10:加权函数 (第659页)(改编自[254](第1071页))展示了在相分数临界梯度 上的加权函数 。
图14.10:加权函数
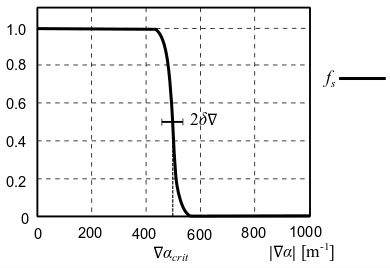
为了通过体积分数及其梯度的标准来检测相边界,使用了相边界的加权函数 :
流动状态混合因子随后计算如下:
以下是翻译成中文的文本:
在哪里