Ansys Fluent 允许您在DPM（离散相模型）功能中使用离散元方法（DEM）。要使用DEM模型，请参阅用户指南中的“使用DEM模型进行碰撞建模”部分。

离散元方法适用于模拟颗粒物质（如碎石、煤、任何材料的珠子）。这类模拟的特点是颗粒体积分数高，颗粒间的相互作用非常重要。需要注意的是，颗粒与流体流动的相互作用可能重要，也可能不重要。典型应用包括：

• 料斗
• 提升管
• 填充床
• 流化床
• 气力输送

12.15.1 理论

DPM功能允许您将移动颗粒模拟为移动质量点，其中使用抽象方法表示颗粒的形状和体积。需要注意的是，忽略了颗粒周围流动的细节（例如，涡流脱落、流动分离、边界层）。利用牛顿第二定律，描述颗粒运动的常微分方程表示如下：

$$m\frac{d\vec{\nu }}{dt}={\vec{F}}_{\mathrm{drag}}+{\vec{F}}_{\mathrm{pressure}}+{\vec{F}}_{\mathrm{virtua}{\mathrm{l}}_{\mathrm{m}}\mathrm{ass}}+{\vec{F}}_{\mathrm{gravitation}}+{\vec{F}}_{\mathrm{other}}\text{\hspace{1em}(12.489)}$$

(12.489)

$$\frac{dx}{dt}=\overrightarrow{v}$$

DEM 实现基于 Cundall 和 Strack [126]（第 1064 页）的工作，并考虑了由颗粒碰撞产生的力（即所谓的“软球”方法）。这些力随后通过公式 12.489（第 577 页）中的 ${\overrightarrow{F}}_{\text{other }}$ 项输入。颗粒碰撞力由变形决定，变形量通过球对之间的重叠（参见图 12.27：用球表示的颗粒（第 577 页））或球与边界之间的重叠来测量。公式 12.489（第 577 页）在时间上进行积分，以捕捉颗粒间的相互作用，使用由材料刚度决定的时间尺度进行积分。

图 12.27：用球表示的颗粒

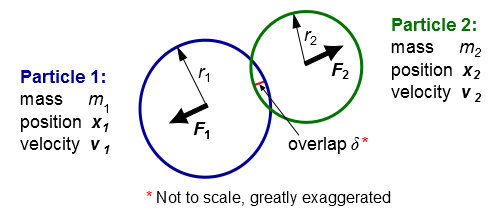
• 未按比例绘制，明显夸大

以下碰撞力定律可供选择：

• 弹簧
• 弹簧-阻尼器
• 赫兹
• 赫兹-阻尼器
• 摩擦
• 滚动摩擦

对于给定的碰撞对，法向接触力的弹簧常数大小至少应满足以下条件：对于该碰撞对中最大的颗粒以及最高的相对速度，弹簧常数应足够高，使得两个碰撞颗粒的反弹重叠量相对于颗粒直径不会太大。您可以使用以下公式估算弹簧常数 $k$ 的值：

$$k=\frac{\pi v^2}{3{\epsilon }_D^2}D\rho$$

其中，$D$ 表示颗粒直径，$\rho$ 是颗粒的质量密度，$v$ 是两个碰撞颗粒之间的相对速度，而 ${\epsilon }_D$ 是允许重叠的直径分数。碰撞时间尺度

被评估为 $\pi \sqrt{\frac{m}{k}}$，这里 $m$ 是颗粒质量（定义为 $\frac{\rho D^3\pi }{6}$）

12.15.1.1 弹簧碰撞定律

对于线性弹簧碰撞定律，定义一个从颗粒1指向颗粒2的单位向量 $\left({\overrightarrow{e}}_{12}\right)$：

$${\overrightarrow{e}}_{12}=\left(x_2-x_1\right)/\Vert \begin{array}{c}{x}_2-x_1\end{array}\Vert$$

其中，$x_1$ 和 $x_2$ 分别表示粒子1和粒子2的位置。

重叠量 $\delta$（在接触期间小于零）定义如下：

$$\delta =\Vert \begin{array}{c}{x}_2-x_1\end{array}\Vert -\left(r_1+r_2\right)$$

其中，$r_1$ 和 $r_2$ 分别表示粒子1和粒子2的半径。

接着，利用你定义的弹簧常数$K$（该值必须大于零）来计算作用在粒子1上的力 $\left({\overrightarrow{F}}_1\right)$：

$${\overrightarrow{F}}_1=K\delta {\overrightarrow{e}}_{12}$$

根据牛顿第三定律，粒子2所受的力$\left({\overrightarrow{F}}_2\right)$为：

$${\overrightarrow{F}}_2=-{\overrightarrow{F}}_1$$

(12.495)

注意，${\overrightarrow{F}}_1$ 的方向是远离粒子2的，因为在接触时 $\delta$ 小于零。

12.15.1.2 弹簧-阻尼碰撞定律

弹簧-阻尼碰撞定律是一种线性弹簧力定律，如前所述，增加了以下描述的阻尼项。

对于弹簧-阻尼碰撞定律，您需要像在弹簧碰撞定律中那样定义一个弹簧常数 $K$，并加上阻尼项的恢复系数 $\left(\eta \right)$。请注意，$0<\eta \le 1$。

在准备进行力计算时，会评估以下表达式：

$$f_{\text{loss }}=\sqrt{{\pi }^2+{\ln }^2\eta }$$

(12.496)

$${\text{m}}_{\text{12}}\text{=}\frac{{\text{m}}_{\text{1}}{\text{m}}_{\text{2}}}{{\text{m}}_{\text{1}}+{\text{m}}_{\text{2}}}$$

(12.497)

$$t_{\mathrm{coll}}=f_{\mathrm{loss}}\sqrt{\frac{m_{12}}{K}}$$

(12.498)

$$\gamma =-2\frac{m_{12}\ln \eta }{t_{\text{coll }}}$$

（12.499）

$${\overrightarrow{v}}_{12}={\overrightarrow{v}}_2-{\overrightarrow{v}}_1$$

其中，$f_{\text{loss }}$ 是损失因子，$m_1$ 和 $m_2$ 分别是粒子1和粒子2的质量，$m_{12}$ 是所谓的“约化质量”，$t_{\text{coll }}$ 是碰撞时间尺度，${\overrightarrow{v}}_1$ 和 ${\overrightarrow{v}}_2$ 分别是粒子1和粒子2的速度，${\overrightarrow{v}}_{12}$ 是相对速度，而 $\gamma$ 是阻尼系数。注意 $\gamma \ge 0$，因为 $\ln \eta \le 0$。

利用上述表达式，可以计算作用在粒子1上的力为：

$${\overrightarrow{F}}_1=\left(K\delta +\gamma \left({\overrightarrow{v}}_{12}\cdot {\overrightarrow{e}}_{12}\right)\right){\overrightarrow{e}}_{12}$$

(12.501)

$\overrightarrow{F_2}$ 的计算使用公式 12.495（第578页）。

12.15.1.3 赫兹碰撞定律

赫兹碰撞定律[240]（第1071页）是一种非线性碰撞定律。采用与“弹簧碰撞定律”部分（第578页）相同的符号表示，粒子1上的力可以描述为：

$${\overrightarrow{F}}_1=K_H{\delta }^{3/2}{\overrightarrow{e}}_{12}$$

(12.502)

在此，常数 $K_H$ 是根据两个碰撞粒子的各自杨氏模量 $E_1$ 和 $E_2$ 以及它们的泊松比 $v_1$ 和 $v_2$ 计算得出的：

$$K_H=\frac{4}{3}\frac{E_1{E}_2}{E_2\left(1-v_1^2\right)+E_1\left(1-v_2^2\right)}\sqrt{\frac{r_1{r}_2}{r_1+r_2}}$$

(12.503)

杨氏模量以帕斯卡为单位，通常在1吉帕到几百吉帕的范围内。泊松比是一个无量纲常数，范围在-1到0.5之间。

$\overrightarrow{F_2}$ 是根据公式12.495（第578页）计算得出的。

12.15.1.4 赫兹-阻尼碰撞定律

赫兹-阻尼碰撞定律是一种非线性碰撞力定律，如赫兹碰撞定律部分（第579页）所述，增加了与线性弹簧-阻尼碰撞定律（见弹簧-阻尼碰撞定律部分，第578页）中相同的阻尼项。也就是说，公式12.502（第579页）被修改如下：

$${\overrightarrow{F}}_1=\left(K_H{\delta }^{3/2}+\gamma \left({\overrightarrow{v}}_{12}\cdot {\overrightarrow{e}}_{12}\right)\right){\overrightarrow{e}}_{12}$$

$\overrightarrow{F_2}$ 是利用方程 12.495（第 578 页）计算得出的。

12.15.1.5 摩擦碰撞定律

摩擦碰撞定律基于库仑摩擦力 $\left(F_{\text{friction }}\right)$ 的方程：

$$F_{\text{friction }}=\mu F_{\text{normal }}$$

(12.505)

其中，$\mu$ 是摩擦系数，$F_{\mathrm{normal}}$ 是垂直于表面力的幅值。摩擦力的方向与相对切向运动相反，并且是否抑制相对切向运动取决于以下因素：

• 切向动量的大小

• 其他切向力的大小（例如，来自重力和阻力的切向分量）

摩擦系数是相对切向速度幅值 $\left(v_{\mathrm{rt}}\right)$ 的函数：

• $v_r\le v_{\text{glide }}$ :

$$-\mu \left(v_r\right)={\mu }_{\text{stick }}+\left({\mu }_{\text{stick }}-{\mu }_{\text{glide }}\right)\left(v_r/v_{\text{glide }}-2.0\right)\left(v_r/v_{\text{glide }}\right)$$

$$\text{-}{v}_{\text{glide }}<v_r\le v_{\text{limit }}\text{:}$$

$$-\mu \left(v_r\right)={\mu }_{\text{glide }}$$

$$\text{-}{v}_r>v_{\text{limit }}\text{:}$$

$$-v_{\text{ratio }}=\frac{\left(v_r-v_{\text{limit }}\right)}{{\text{ slope }}_{\text{limit }}}$$

$$-{\mu }_{\text{ratio }}=\frac{{\mu }_{\text{glide }}}{{\mu }_{\text{limit }}}$$

$$-\mu \left(v_r\right)={\mu }_{\text{glide }}\frac{1+v_{\text{ratio }}}{1+{\mu }_{\text{ratio }}{v}_{\text{ratio }}}$$

${\mu }_{\text{stick }}$ 是粘滞摩擦系数

${\mu }_{\text{glide }}$ 是滑动摩擦系数

${\mu }_{\text{limit }}$ 是高速极限摩擦系数

$v_{\text{glide }}$ 是滑动速度 - 对于较低速度，$\mu$ 以二次插值方式在 ${\mu }_{\text{stick }}$ 和 ${\mu }_{\text{glide }}$ 之间变化

$v_{\text{limit }}$ 是极限速度 - 对于较高速度，$\mu \left(v_r\right)$ 趋近于 ${\mu }_{\text{limit }}$

${\text{slope}}_{\text{limit }}$ 是一个参数，决定 $\mu \left(v_r\right)$ 趋近于 ${\mu }_{\text{limit }}$ 的速度

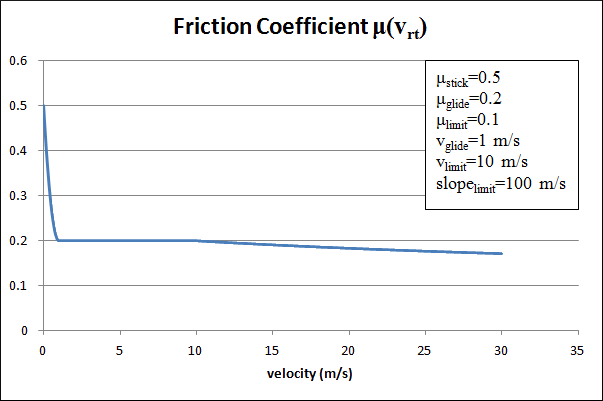
关于 $\mu \left(v_{\mathrm{rt}}\right)$ 的图表示例，请参见图 12.28：摩擦系数图表示例（第 581 页）。

图 12.28：摩擦系数图表示例

12.15.1.6 DEM 滚动摩擦碰撞定律

滚动摩擦碰撞定律是基于库仑摩擦方程 $\left(F_{\text{rolling }}\right)$ 的摩擦碰撞定律（摩擦碰撞定律（第 580 页））的扩展。

$$F_{\text{rolling }}={\mu }_{\text{rolling }}{F}_{\text{normal }}$$

(12.506)

其中，${\mu }_{\text{rolling }}$ 是滚动摩擦系数，而 $F_{\text{normal }}$ 是垂直于颗粒表面或从一个颗粒中心指向另一个颗粒中心的力的幅值。滚动摩擦力 ${\overrightarrow{F}}_{\text{rolling }}$ 仅作用于颗粒与颗粒或颗粒与壁面接触点的局部扭矩上。这种力可能会也可能不会抑制相对角速度，具体取决于相对扭矩的大小。

12.15.1.7 DEM 颗粒包

对于典型应用，单独追踪所有颗粒的计算成本是高昂的。因此，离散元方法的处理方式与 DPM 类似，即将相似的颗粒分成颗粒包，然后通过追踪单个代表性颗粒来确定每个颗粒包的位置。DEM 方法与 DPM 的区别如下：

• 在 DEM 计算碰撞时使用的质量是整个颗粒包的质量，而不仅仅是单个代表性颗粒的质量。

• DEM 颗粒包的半径是这样一个球的半径，其体积等于整个颗粒包的质量除以颗粒密度。

12.15.1.8 笛卡尔碰撞网格

在评估颗粒包之间的碰撞时，直接进行涉及所有颗粒包的力评估成本过高。考虑一下，对于 $N$ 个颗粒包，需要评估的

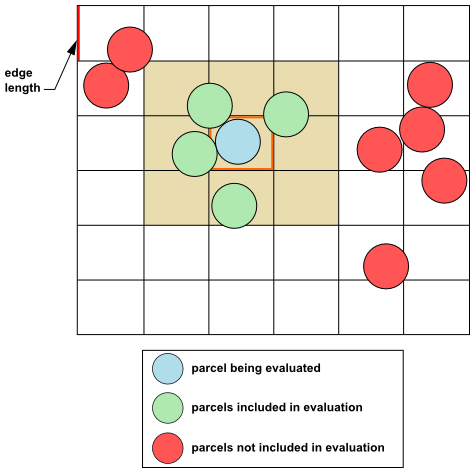
每次时间步长都需要检查的次数大约是 $N^2$。为了解决这个问题，采用了一种几何方法：通过一个合适的笛卡尔网格（网格单元的边长是最大颗粒直径的倍数）将域分割，然后仅对位于相邻网格单元中的颗粒进行力评估，因为碰撞网格中更远的单元中的颗粒事先已知是不可及的。参见图 12.29：颗粒的力评估（第 582 页）以获得图示说明。

图 12.29：颗粒的力评估