在多个工业流体流动应用中,存在具有尺寸分布的次级相。颗粒的尺寸分布,包括固体颗粒、气泡或液滴,可以在多相系统中的传输和化学反应过程中演变。这种演变过程可以是诸如成核、生长、分散、溶解、聚集和破裂等不同现象的组合,从而产生分散体。因此,在涉及尺寸分布的多相流中,除了动量、质量和能量平衡外,还需要一个平衡方程来描述颗粒群的变化。这种平衡通常被称为群体平衡。群体平衡适用的案例包括结晶、气相或液相中的沉淀反应、气泡柱、气体分散、喷雾、流化床聚合、造粒、液-液乳化和分离以及气溶胶流动。
本章节描述了Ansys Fluent中可用的群体平衡模型的理论基础。本章内容组织如下:
14.9.1 简介
为了利用这一建模概念,引入了一个数密度函数来描述颗粒群。借助颗粒属性(例如,颗粒大小、孔隙度、组成等),可以区分群体中的不同颗粒并描述它们的行为。
Ansys Fluent提供了三种求解群体平衡方程的方法:离散群体平衡法、标准矩方法和正交矩方法。
- 14.9.1.1 离散方法
- 14.9.1.2 非均匀离散方法
- 14.9.1.3 标准矩方法
- 14.9.1.4 正交矩方法
14.9.1.1 离散方法
在离散方法中,颗粒群被离散化为有限数量的粒径区间。这种方法的优点在于可以直接计算颗粒粒径分布(PSD)。当颗粒尺寸范围已知且不超过两到三个数量级时,这种方法尤为适用。在这种情况下,可以用相对较少的粒径区间对颗粒群进行离散化,并计算与流体动力学耦合的粒径分布。离散方法的缺点是,如果需要大量的区间,计算成本会很高。
14.9.1.2 非均匀离散方法
现有均匀离散方法的一个局限性在于,所有区间都被分配给相同的次相,因此以相同的相动量进行平流。这对于模型中大颗粒和小颗粒由于不同的动量场而可能发生分离的情况是不适用的。非均匀离散方法通过允许将区间组以不同的相速度进行平流,克服了这一局限。因此,当激活非均匀离散模型时,群体平衡模型可以应用于多个次相。
离散区间分数 的一般输运方程可以写为:
由于在均匀离散方法中,所有箱子都属于同一相,因此在发生破裂和团聚的情况下,该相的净质量源为零,可以表示为:
如图14.16所示(第785页),均匀离散方法中所有箱子都以相同的相速度进行平流。相比之下,图14.17所示(第785页)的非均匀离散方法允许将箱子分配给多个相。在这里,每个相有个箱子,分布在个相上,总共是个箱子。箱子和分别以相速度等进行平流。由于给定相中的箱子可以通过破碎或团聚迁移到另一个相,因此任何给定相中箱子源的总和不一定等于零,从而为该相创造了一个净质量源。
给定相的净质量源可以表示为属于该相的箱子源的总和。
对于断裂和聚结,所有相源的总和为零。
与同质离散模型也颇为相似。
重要提示:非均匀离散方法目前仅限于破碎和聚结过程。
图14.16:均匀离散方法
各箱子通过破碎和聚结相互作用
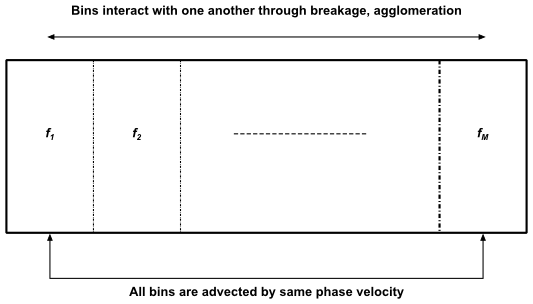
所有箱子以相同的相速度平流
图14.17:非均匀离散方法
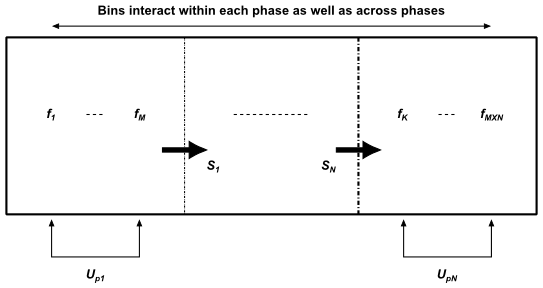
14.9.1.3 矩方法标准方法
矩方法标准方法(SMM)是离散群体平衡方法的一种高效替代方案。在这种方法中,群体平衡方程被转化为一组关于分布矩的输运方程。第 矩是通过在整个粒子空间内对粒子属性提升到第 次幂的数密度进行积分来定义的。通常只需要求解少数几个矩方程,通常是三到六个。这相比于离散方法可能显著减少了需要求解的方程数量。除了计算优势外,当不需要整个分布而只需要某些平均和总量来表示粒子分布时,SMM方法非常有用。通常,零阶矩表示总数密度,二阶矩表示单位体积的总表面积,三阶矩表示总质量密度。
在SMM方法中,不对尺寸分布做任何假设,并且矩方程以封闭形式表述,仅涉及矩本身的函数。然而,这种精确的封闭要求构成了严重限制,因为聚结(常数聚结核除外)和破碎现象不能写成矩的函数。
14.9.1.4 矩的正交方法
矩量配方法(QMOM)在计算成本方面与SMM具有类似的优势,但用近似闭包取代了SMM所需的精确闭包。这使得QMOM能够广泛应用于各种场景,没有任何限制。
14.9.2 群体平衡模型理论
本章概述了用于Ansys Fluent中预测颗粒生长和成核的方法的理论和控制方程。
- 14.9.2.1 颗粒状态向量
- 14.9.2.2 群体平衡方程(PBE)
- 14.9.2.3 求解方法
- 14.9.2.4 群体平衡统计
14.9.2.1 颗粒状态向量
颗粒状态向量由一组“外部坐标”(表示颗粒的空间位置)和“内部坐标”(可能包括颗粒大小、成分和温度)来表征。基于这些坐标,可以假设一个数密度函数 ,其中 。因此,在无穷小体积 中的颗粒平均数量为 。相比之下,连续相状态向量由 给出。
整个系统中的颗粒总数为
物理空间中的局域平均数密度(即单位体积内的粒子总数)由以下公式给出:
所有颗粒的总体积分数由以下公式给出:
其中, 表示处于状态 的粒子的体积。
14.9.2.2 群体平衡方程(PBE)
假设 代表粒子体积,那么数量密度函数的传输方程可表示为
边界条件和初始条件设定如下:
其中, 表示成核速率,单位是粒子数每立方米每秒。
14.9.2.2.1 粒子生长
基于粒子体积的生长速率,记作 ,其单位为立方米每秒,定义为
基于颗粒直径(或长度)的增长率定义为
单个粒子的体积 ( V ) 被定义为 ( K_v L^3 ),因此 ( G_v ) 与 ( G ) 之间的关系是
单个颗粒的表面积 定义为 。因此,对于立方体或球体,。
重要提示:
-
在颗粒溶解的情况下,由于颗粒体积的减小,颗粒体积增长率是负的。
-
在由于密度(压力)变化导致的气泡膨胀情况下,方程 14.697(第 787 页)中的增长率 是气泡体积膨胀的速率。
考虑 为一个体积为 且密度为 的气泡的质量,
对于常数 (无质量转移的气泡膨胀),,因此
在 Mills 的论文 [443](第1082页)中可以找到更详细的解释。
14.9.2.2.2 由于破碎和聚集导致的颗粒生成与消亡
颗粒的生成和消亡是由于破碎和聚集过程引起的。破碎过程的例子包括结晶器中的晶体断裂和泡罩塔中由于液体湍流引起的气泡破碎。同样,聚集可以由结晶器中的颗粒团聚和泡罩塔反应器中的气泡合并引起。
请注意,在 FLUENT 群体平衡模型中,所有的破碎和聚集事件都被建模为二元的,除了广义破碎核。
14.9.2.2.2.1 破碎
破碎速率表达式,或称为核 [400](第1080页),被表示为
其中
破碎频率;即,体积为 的颗粒在单位时间内破碎的分数
概率密度函数(PDF),表示从体积 破碎成体积为 的颗粒的概率
破碎因子,用于校准破碎核
体积为 的颗粒因破碎而产生的出生率由以下公式给出:
在单位时间内,体积为 的粒子中,有 个粒子发生破碎,产生 个新粒子,其中比例为 的粒子体积为 。这里, 表示每个母粒子破碎后产生的子粒子数量(例如,二元破碎产生两个粒子)。
由于破碎导致的体积为 的粒子的死亡率由以下公式给出:
PDF 也被称为颗粒破碎分布函数,或子颗粒大小分布。虽然已经提出了几种破碎分布函数的形式,但必须满足以下物理约束:归一化的破碎颗粒数量总和必须为1,碎片的质量总和必须等于原始颗粒的质量,并且形成的碎片数量必须正确表示。
数学上,这些约束可以写成如下形式:
- 对于归一化条件:
- 质量守恒
对于二元断裂, 相对于 是对称的;也就是说,
以下是Ansys Fluent中可用于计算破碎频率的模型列表:
-
常数值
-
Luo模型
-
Lehr模型
-
Ghadiri模型
-
Laakkonen模型
-
Liao模型
-
用户自定义模型
Ansys Fluent提供了以下模型用于计算破碎概率密度函数(PDF):
-
抛物线PDF
-
Laakkonen PDF
-
多破碎碎片通用PDF
-
用户自定义模型
破碎频率模型以及抛物线和通用PDF将在后续章节中详细描述。
14.9.2.2.2.2 Luo和Lehr破碎核
Luo和Lehr模型是综合核模型,涵盖了破碎频率和破碎颗粒的PDF。
其一般形式是对撞击直径为(及体积为)的颗粒的涡流大小进行积分。积分是在无量纲涡流大小 = / 上进行的。一般形式为
参数如表14.4所示:Luo模型参数(第790页)和表14.5:Lehr模型参数(第790页)。
表14.4:Luo模型参数
| m | |||
|---|---|---|---|
| 11/3 | 其中 | -1/3 | |
详细符号说明请参见 Luo [400](第 1080 页)。
表 14.5:Lehr 模型参数
| 13/3 | -2/3 |
其中, 通过图形用户界面输入。参见 Lehr [353](第 1077 页)。
14.9.2.2.2.3 Ghadiri 破碎核
与 Luo 和 Lehr 模型相反,Ghadiri 模型 [201](第 1068 页),[460](第 1083 页)仅用于模拟固体颗粒的破碎频率。您需要指定概率密度函数(PDF)模型来定义子代分布。
破碎频率 定义为:
其中, 表示颗粒速度, 表示破碎前的颗粒直径。破碎常数 决定了每秒钟有多少母颗粒发生破碎的总体规模。这一常数取决于具体情况,并与颗粒的特性成正比:
其中, 表示颗粒密度, 为颗粒的弹性模量, 则是界面能。请注意,您可能需要调整 ,例如通过与基准实验校准来进行调整。
14.9.2.2.2.4 Laakkonen 破碎核
Laakkonen 破碎核表示为破碎频率 与子代概率密度函数 的乘积,其中
其中, 表示液相涡流耗散率, 为表面张力, 是液体密度, 是气体密度, 为母粒子直径, 是液体粘度。
常数 , 和 。
子粒径分布函数(daughter PDF)由以下公式给出:
其中, 和 分别表示子颗粒和母颗粒的体积。该模型是广泛使用的 Luo 模型的有用替代方案,因为它具有简单的子颗粒概率密度函数表达式,因此需要显著较少的计算工作量。
14.9.2.2.2.5 Liao 破碎核函数
在流动液体中的气泡会受到应力 ,该应力会使气泡变形,一旦应力超过表面张力的恢复效应 ,气泡最终会破碎,如图 14.18 所示:气泡破碎(第 791 页)(改编自 [369](第 1078 页))。
图 14.18:气泡破碎

基于 Martínez-Bazán 等人的工作 [416](第 1081 页),Liao [369](第 1078 页)提出将尺寸为 的气泡的破碎频率定义为应力 和临界应力 的关系如下:
其中, 表示子气泡的直径。
结合破碎方法用于根据能量准则和力准则来确定临界应力。对于二元破碎,即气泡 分裂成两个气泡 和 时, 可以表示为:
能量约束 由断裂过程中表面能的增加所决定:
其中, 表示气泡的表面能量,而气泡 的大小则是根据气泡 和 的大小计算得出的,具体如下:
力约束 由最小子气泡的毛细力决定:
其中, 是表面张力系数。
破坏应力 导致气泡破裂,这是由气泡表面上的速度梯度引起的。在湍流中,速度变化可能由多种机制引起,例如湍流脉动、平均流动中的速度梯度、湍流涡旋和界面阻力 [369](第 1078 页),如图 14.19 所示:湍流中的气泡破碎机制(第 792 页)(改编自 [369](第 1078 页))。
图 14.19:湍流中的气泡破碎机制
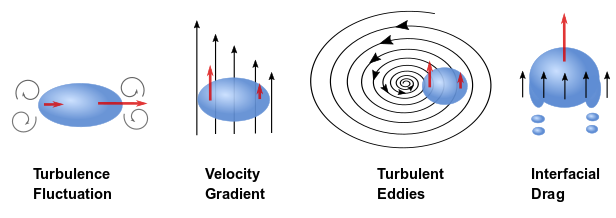
这些破碎机制的应力表示为:
- 由湍流速度脉动引起的惯性力:
- 由于主流流速梯度引起的粘性剪切力:
其中, 是液体密度, 是液体相中的湍流耗散率, 是Kolmogorov微尺度。
其中, 表示液体的动力粘度, 则是体相中的剪切应变率。
- 由涡流中速度梯度引起的粘性剪切力:
其中, 表示最小涡流中流动的特征应变率。
- 界面阻力(或摩擦):
其中, 和 分别表示气泡 的终端速度和阻力系数。
常数 、、 和 用于考虑不同机制引起的破坏应力估计中的不确定性。系数默认(并由 Liao [369] (第 1078 页) 推荐)值为:,以及 。
14.9.2.2.2.6 抛物线型概率密度函数 (PDF)
破碎概率密度函数 (PDF) 包含了由破碎事件形成的碎片的概率信息。它提供了颗粒的数量以及从破碎中可能得到的大小分布。Ansys Fluent 中实现的抛物线型 PDF 形式使您能够定义破碎 PDF,从而...
其中, 和 分别表示子颗粒和母颗粒的体积。形状因子 的取值不同,颗粒破碎分布函数的形状也会表现出不同的行为。例如,若 ,颗粒破碎呈现均匀分布。若 ,则得到一个凹形抛物线,意味着获得大小不均的碎片比均等大小的碎片更为可能。相反,对于 的情况,则更倾向于获得均等大小的碎片。超出 0 到 3 范围的值是不允许的,因为概率密度函数(PDF)不能取负值。
需要注意的是,方程 14.724(第 793 页)中定义的 PDF 关于 对称。
14.9.2.2.2.7 广义 PDF
Ansys Fluent 中实现的广义 PDF 形式使您能够模拟多个破碎碎片(即大于两个),并指定子分布的形式(例如,均匀分布、等尺寸、磨损、幂律、抛物线、二元贝塔分布)。该模型既可应用于离散方法,也可用于 QMOM。
考虑到自相似公式 [539](第 1088 页),其中相似性 是子颗粒与母颗粒大小的比值(即 ),那么广义 PDF 可表示为
其中, 是自相似的女儿分布 [141](第1065页)。 的第 阶矩,记作 ,
哪里
随后,数量守恒和质量守恒的条件可以表述为
[141](第1065页)的广义形式可以表示为
其中,可以是0或1,分别表示由1个或2个项组成。对于每个项,是权重因子,是子颗粒的平均数量,和是指数,而是beta函数。在方程14.730(第794页)中,对参数施加了以下约束:
为了展示如何将广义PDF转换为表示适当的子分布,请考虑以下表格中所示的表达式:
表14.6:子分布
| 类型 | |
|---|---|
| 等大小 [321] (p. 1075) | |
| 磨损 [321] (p. 1075) | |
| 幂律 [674] (p. 1096) | |
| 抛物线 -a [674] (p. 1096) | |
| 奥斯汀 [34] (p. 1059) | |
| 二元贝塔 -a [259] (p. 1072) | |
| 二元贝塔 -b [420] (p. 1081) | |
| 均匀 [674] (p. 1096) |
表14.7:女儿分布(续)
| 类型 | 约束条件 | |
|---|---|---|
| 等大小 [321] (p. 1075) | p | |
| 磨损 [321] (p. 1075) | 2 | |
| 幂律 [674] (p. 1096) | ||
| 抛物线 -a [674] (p. 1096) | ||
| 奥斯汀 [34] (p. 1059) | ||
| 二元贝塔 -a [259] (p. 1072) | 2 | N/A |
| 二元贝塔 -b [420] (p. 1081) | 2 | |
| 均匀 [674] (p. 1096) |
在表14.6:子分布(第795页)中, 是狄拉克δ函数, 是权重系数,而 和 是用户定义的参数。
通过使用表14.8:广义形式中子分布的值(第796页)所示的数值,广义形式可以表示表14.6:子分布(第795页)中的子分布。
表14.8:广义形式中子分布的值
| 类型 | w0 | w1 | 约束条件 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 等尺寸 | 1 | 0 | 00* | N/A | N/A | N/A | N/A | ||
| 损耗 | 0.5 | 2 | 1 | 0.5 | 2 | 1 | |||
| 幂律 | 1 | 1 | N/A | N/A | N/A | N/A | |||
| 抛物线 | 1 | 2 | N/A | N/A | N/A | N/A | |||
| 奥斯汀 | w | 1 | 1 | ; | |||||
| 二元贝塔 ** | 1 | 2 | N/A | N/A | N/A | N/A | |||
| 均匀分布 | 1 | 1 | N/A | N/A | N/A | N/A |
(*) 你可以通过使用一个非常大的数字来近似无穷大,例如 1e20。
(**) 当 时,Binary Beta -a 是 Binary Beta -b 的一个特例。
重要提示:请注意,对于 Ansys Fluent 中广义形式的 PDF 实现,您只需输入 和 的值,其余的值 和 ) 将自动计算。
14.9.2.2.2.8. Martinez-Bazan 破碎核
Martinez-Bazan 破碎频率 [416](第 1081 页)通常用于模拟搅拌槽反应器中的气泡破碎。该核提供了一个基于湍流应力和表面张力局部值的气泡破碎速率的现象学表达式。破碎速率表示为:
最大稳定气泡直径 由以下公式给出:
在上述方程中,
和 实验确定的常数
母泡直径
湍流耗散率
表面张力
液体密度
14.9.2.2.2.9 倒U形概率密度函数
大多数气泡破碎的子分布概率密度函数(PDFs)假设了一个对称的U形分布,其中等尺寸子气泡的破碎概率最小。尽管这种子分布函数在许多应用中效果良好,但[416](第1081页)中还提出了一种替代的倒U形分布,与U形分布相反,等尺寸子气泡的形成概率被假设为最大。在Ansys Fluent中,这一分布实现如下:
其中,,,,而的定义见破裂部分(第788页)。
14.9.2.2.2.10. 聚合
聚合核函数[400](第1080页)表示为
其中, 是一个用于校准聚合核的聚合因子。
聚合核的单位是 ,有时被定义为两个量的乘积:
-
体积为 的粒子与体积为 的粒子之间的碰撞频率
-
“聚合效率”(即体积为 的粒子与体积为 的粒子聚合的概率)。
体积为 的粒子因聚合而产生的生成速率由下式给出:
体积为 的粒子与体积为 的粒子聚集,形成体积为 的粒子。因子 的引入是为了避免对每个碰撞事件进行重复计数。
体积为 的粒子因聚集导致的消亡速率由以下公式给出:
重要提示:破碎和聚结核函数取决于物理应用的性质。例如,在气液分散体系中,这些核函数是局部液相湍流耗散率的函数。
以下是Ansys Fluent中可用的聚结函数列表:
-
常数 -
Luo模型 -
自由分子模型 -
湍流模型 -
Prince和Blanch模型 -
Liao模型 -
用户自定义模型
Luo模型、自由分子模型、湍流模型、Prince和Blanch模型以及Liao模型的聚结函数将在后续章节中详细描述。
14.9.2.2.2.11.Luo聚结核函数
对于Luo模型[398](第1080页),一般的聚结核函数定义为由于体积为和的颗粒二元碰撞而形成的颗粒体积速率:
其中, 表示碰撞频率,而 则是碰撞导致聚结的概率。碰撞频率的定义如下:
其中, 表示直径为 和 的两个粒子之间的特征碰撞速度。
以下文本的中文翻译:
聚合概率的表达式为:
其中, 是一个数量级为1的常数,, 和 分别表示主相和次相的密度,而韦伯数定义为
14.9.2.2.2.12 自由分子聚集核
真实粒子以频率(或核)聚集和破碎,这些频率(或核)具有复杂的依赖关系,涉及粒子的内部坐标 [584](第1090页)。特别是,非常小的粒子(例如,直径可达 )由于布朗运动引起的碰撞而聚集。在这种情况下,碰撞频率与粒子大小有关,通常采用以下核函数:
其中, 是玻尔兹曼常数, 是绝对温度, 是悬浮流体的粘度, 和 分别是粒子 和 的直径(或长度)。这个核函数也被称为布朗核或邻位核。
14.9.2.2.2.13 湍流聚合核
在混合过程中,机械能被提供给流体。这种能量在流体中产生湍流。湍流产生涡旋,进而有助于能量耗散。能量从最大的涡旋传递到最小的涡旋,在其中通过粘性相互作用耗散。最小的涡旋的尺寸是科尔莫戈罗夫微尺度,,它表示为运动粘度和湍流动能耗散率的函数:
在湍流流场中,聚集可以通过两种机制发生:
-
粘性子范围机制:当颗粒小于科尔莫戈罗夫微尺度 时,适用此机制。
-
惯性子范围机制:当颗粒大于科尔莫戈罗夫微尺度时,适用此机制。在这种情况下,颗粒具有独立的速率。
对于粘性子范围,颗粒碰撞受涡流内局部剪切的影响。根据萨夫曼和特纳 [564](第1089页)的工作,碰撞率表示为,
其中, 是一个预因子,考虑了湍流碰撞的捕获效率系数,而 是剪切速率:
在惯性子区,颗粒大于最小的涡流,因此它们受到流场中速度波动的影响而被拖拽。在这种情况下,聚并速率采用Abrahamson模型[6](第1057页)来表达。
其中,表示粒子的均方速度。
湍流碰撞的经验捕获效率系数描述了碰撞粒子之间的水动力和吸引相互作用。Higashitani等人[245](第1071页)提出了以下关系:
其中, 表示黏性力与范德华力之间的比值。
其中, 为哈梅克常数,是颗粒材料的函数,而 则为变形速率。
14.9.2.2.2.14 Prince和Blanch聚合核
Prince和Blanch的聚合模型[535](第1088页)假设两个气泡的聚合过程分为三个步骤:
-
气泡碰撞,其间夹带少量液体。
-
分离气泡的液膜排液,直至达到临界厚度。
-
液膜破裂,气泡合并成一个大气泡。
此聚合核通过两个气泡的碰撞速率以及与聚合所需时间相关的碰撞效率来建模。
碰撞效率通过比较聚并所需时间 ( t_{ij} ) 与碰撞过程中实际接触时间 ( \tau_{ij} ) 来进行建模:
其中:
及:
在公式14.756(第800页)和公式14.757(第801页)中, 表示液体密度, 代表表面张力, 是初始膜厚度, 是破裂发生时的临界膜厚度, 表示液体的湍流涡流耗散,而 则是定义为等效半径的参数:
其中, 和 分别表示气泡 和 的半径。
湍流对碰撞频率的贡献被建模为:
碰撞粒子横截面积的定义如下:
湍流速度由以下公式给出:
是一个校准因子,用于调整湍流贡献。
浮力对碰撞频率的贡献计算方式如下:
其中:
而 是浮力的校准因子。
在公式 14.760(第 801 页)、公式 14.761(第 801 页)和公式 14.763(第 801 页)中, 和 分别是气泡 和 的直径, 是重力加速度。
目前忽略了剪切对碰撞频率的贡献(公式 14.754(第 800 页)中的 )。
14.9.2.2.2.15 廖氏聚合核
聚结发生在两个或多个流体颗粒碰撞时。这可能由于多种原因发生,如湍流、涡流捕获、平均流动中的速度梯度、体积力以及尾流卷吸等,如图 14.20 所示:湍流中的气泡碰撞(第 802 页)(改编自 [369](第 1078 页))。
图 14.20:湍流中的气泡碰撞
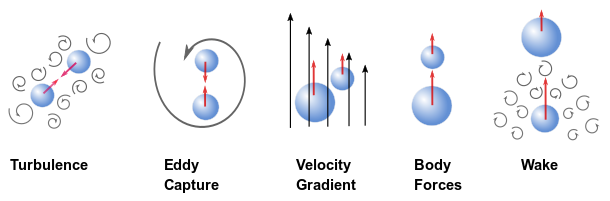
假设所有聚结机制的累积贡献,廖 [369](第 1078 页)提出了一种计算两个体积分别为 和 的气泡之间二元碰撞总聚结频率 的公式。
其中, 表示气泡填充极限,而 是其最大值。当气泡相的局部体积分数接近最大填充极限 时,气泡合并速率无限增大。
由于气泡间的碰撞可能导致合并或反弹,因此使用合并效率(或概率)。合并频率 表示为碰撞频率 与每次碰撞事件效率 的乘积:
类似于动力气体理论,碰撞频率 ( h ) 近似为两个粒子在单位时间内扫过的体积:
其中, 表示两气泡间的相对速度,而 则为碰撞的有效横截面积。
对于由湍流波动引起的随机气泡碰撞,其有效横截面积为:
其中, 和 分别代表气泡 和 的直径。
气泡 和 之间的相对速度估计如下:
其中, 是在距离 上的湍流速度,具体由以下公式给出:
其中, 表示液相中的湍流动能耗散率。
对于由湍流引起的碰撞,气泡 与气泡 之间的聚并频率 可表示为:
其中, 是一个常数,而 是在惯性碰撞区域中的聚并效率。方程 14.770(第 803 页)适用于远大于 Kolmogorov 长度尺度的气泡。
当考虑浮力效应时,只有在向上流动中,较快的气泡从下方接近较慢的气泡时,才会发生碰撞。聚并频率 被建模为:
其中, 是一个常数,而 和 分别表示气泡 和气泡 的终端速度。有效聚并效率 的计算公式如下:
其中, 是 Kolmogorov 长度尺度。
惯性碰撞的聚并效率 表示为:
系数 的默认值为 5.0,
其中, 表示液体密度, 代表表面张力系数,而
粘性碰撞的聚并效率 表示为:
其中, 是液体的动力粘度, 是哈梅克常数,表示宏观物体间范德华相互作用的强度, 是流体在最小涡流中的特征应变速率。对于空气-水界面,其值近似为 。
在剪切诱导的碰撞中,气泡只能从高速度侧沿着主流速度方向与它跟随的另一个气泡发生碰撞。由速度梯度引起的气泡 和气泡 之间的合并频率 表示为:
其中, 是一个常数, 是整体流动的剪切应变率,而 由方程 14.772(第 803 页)定义。
对于远小于 Kolmogorov 微尺度的气泡,其碰撞被认为是受粘性力控制的。聚并频率 被建模为:
其中, 是一个常数。它可以从 Kolmogorov 尺度推导得出:
当一个直径大于临界尺寸的气泡在液体中移动时,它会在其后方的液体相中产生尾流。位于前导气泡尾流区域内的跟随气泡可以被加速并达到前导气泡。尾流裹挟的聚并效率被建模为:
其中, 是一个常数, 和 分别是气泡 和 的终端速度,而 和 分别是气泡 和 的阻力系数。气泡 的混合函数 定义为:
临界直径 的计算公式如下:
其中 是气体密度。
常数 、、、 和 用于考虑在不同条件下相对速度估计的不确定性。Liao [369](第1078页)建议将这些系数设置为1.0,这也是Ansys Fluent中的默认设置。
14.9.2.2.3 粒子成核生成
根据应用的不同,粒子可能会由于主要相中分子的转移而自发成核。例如,在溶液结晶过程中,第一步是相分离或“新生”新晶体。在沸腾应用中,第一个蒸汽泡的产生是一个成核过程,称为核沸腾。
成核速率通过边界条件定义,如公式14.698(第787页)所示。
14.9.2.3 求解方法
如前所述,Ansys Fluent 中的人口平衡方程可以通过四种不同的方法求解:离散方法、非均匀离散方法、标准矩方法(SMM)和四阶矩方法(QMOM)。对于每种方法,Ansys Fluent 的实现仅限于对应于粒子大小的单一内部坐标。以下小节描述了每种方法的理论背景,并列出了它们的优缺点。
14.9.2.3.1 离散方法和非均匀离散方法
14.9.2.3.2 标准矩方法(SMM)
14.9.2.3.3 四阶矩方法(QMOM)
14.9.2.3.4 直接四阶矩方法(DQMOM)
14.9.2.3.1 离散方法和非均匀离散方法
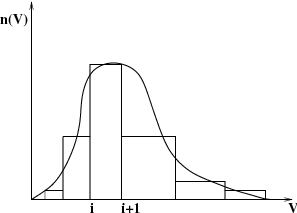
离散方法(也称为分类或分段方法)由Hounslow [256](第1071页)、Litster [384](第1079页)和Ramkrishna [539](第1088页)开发。该方法基于将连续的颗粒尺寸分布(PSD)表示为一组离散的尺寸类别或区间,如图14.21所示:离散方法表示的颗粒尺寸分布(第805页)。这种方法的优点在于其稳健的数值计算和直接给出PSD的能力。缺点是需要预先定义区间,并且可能需要大量的类别。
非均匀离散方法的求解方法基于离散方法,因此共享许多相同的基本原理。
图14.21:离散方法表示的颗粒尺寸分布
14.9.2.3.1.1 数值方法
在Ansys Fluent中,PBE以颗粒尺寸的体积分数形式编写:
其中, 表示次相的密度, 表示颗粒尺寸 的体积分数,定义为
以下是翻译成中文的文本:
在哪里
而 表示粒径为 的颗粒体积。在 Ansys Fluent 中,引入了一个称为 的分数作为解变量,这个分数被定义为
其中, 表示次级相的总体积分数。
成核速率 出现在描述最小尺寸 的体积分数的离散化方程中。符号 表示这个特定项,即 ,仅在最小颗粒尺寸的情况下出现在方程 14.783(第 805 页)中。
生长速率,如方程 14.783(第 805 页)[256](第 1071 页)所示,其离散化如下:
体积坐标被离散化为 [256](第 1071 页),其中 ,并被称为“比率因子”。
粒子的生成和消亡率定义如下:
其中,,
表示由粒子 和 聚集形成的粒子体积,其定义如下:
以下文本的中文翻译:
如果 大于或等于最大颗粒尺寸 ,那么对类别 的贡献为
重要提示:请注意,对于最小的颗粒类别,不存在破碎现象。
14.9.2.3.1.2 离散方法的破碎公式
Ansys Fluent 中离散方法的默认破碎公式基于 Hagesather 方法 [224](第 1070 页)。在该方法中,破碎源被分配到相应的尺寸区间,同时保持质量和数量密度不变。当相邻区间尺寸比可以表示为 ,其中 时,第 个区间()的源项可以表示为
这里
Ramkrishna [326](第1076页)提供了一种更为严谨的数学表达方式,其中破碎率被表示为...
哪里
Ramkrishna公式可能由于所需积分点数量庞大而计算较慢。然而,对于简单的形式,积分可以相对容易地进行。Hagesather公式所需的积分点较少,通过适当选择分箱大小,其与Ramkrishna公式的精度差异可以得到校正。
重要提示:为了保持计算时间合理,当Luo模型与Ramkrishna公式结合使用时,采用体积平均值来表示湍流涡流耗散。
注意:非均匀离散相应用Hagesather公式。
14.9.2.3.2 标准矩方法(SMM)
SMM由Randolph和Larson提出[540](第1088页),是求解PBE的另一种方法。其优点在于降低了问题的维度,并且求解低阶矩的传输方程相对简单。缺点是只有在恒定聚集和尺寸无关增长的情况下才能实现右侧的精确闭合,并且无法进行破碎建模。然而,通过QMOM(参见第809页的矩量法(QMOM))克服了闭合约束。
14.9.2.3.2.1 数值方法
SMM方法基于对PBE关于内部坐标(在此情况下为颗粒尺寸)取矩。
定义矩为
假设颗粒持续增长,其传输方程可以表示为:
此处
表示指定的时刻数量,而 则是成核速率。生长项被定义为
以下文本翻译成中文为:而持续增长则表现为
公式14.802可以通过以下方法推导出:
并反转积分顺序。基于这些矩量,可以推导出描述粒子群体总体特性的参数。
这些特性与混合悬浮液每单位体积中固态颗粒的总数、长度、面积和体积有关。通常使用索特平均直径 作为平均粒径。
为了封闭方程 14.801(第 808 页),需要用正在求解的矩来表示方程 14.802(第 808 页)至方程 14.805(第 808 页)中的量。为此,一种方法是假设与粒径无关的破碎和聚集核,以及其他简化,如对项 进行泰勒级数展开。或者,可以假设粒度分布(PSD)的轮廓,以便可以对方程 14.802(第 808 页)至方程 14.805(第 808 页)进行积分,并用正在求解的矩来表示。
在 Ansys Fluent 中,通过限制 SMM 应用于粒径无关生长和恒定聚集核的情况,实现了精确封闭。
14.9.2.3.3 矩量法(QMOM)
矩量法(QMOM)由 McGraw [422](第 1081 页)首次提出,用于模拟气溶胶演化和凝聚问题。Marchisio 等人 [413](第 1081 页)的应用表明,该方法需要相对较少的标量方程来跟踪人口矩,且误差较小。
当需要聚集量而不是精确的 PSD 时,QMOM 提供了一种有吸引力的离散方法替代方案。其优点是变量较少(通常只有六个或八个矩),并且动态计算尺寸区间。缺点是可能没有足够的横坐标来描述 PSD,并且求解乘积差分算法可能耗时较长。
14.9.2.3.3.1 数值方法
正交多项式序列的确定基于与(即颗粒尺寸分布)正交的原理。若正交近似的横坐标为阶数为的多项式的节点,则该正交近似即为所求。
如果 是一个次数为 或更小的多项式 [140](第1065页),则该方法是精确的。在其他情况下, 越接近一个多项式,近似就越准确。
计算正交近似的一种直接方法是利用其通过矩的定义:
阶数为 的正交逼近由其 个权重 和 个横坐标 定义,并且可以通过其前 个矩 来计算,方法是根据矩 写出多项式的递归关系。一旦这种关系以矩阵形式写出,就很容易证明多项式的根对应于雅可比矩阵 [534](第 1088 页)的特征值。此过程称为矩逆算法,它使用乘积差算法 [213](第 1069 页)或惠勒算法 [705](第 1098 页)。一旦知道了权重和横坐标,就可以计算由于聚结和断裂产生的源项,从而可以求解矩的输运方程。
应用公式 14.813(第 809 页)和公式 14.814(第 810 页),公式 14.801(第 808 页)中的产生和消亡项可以重写为
从理论上讲,在使用QMOM时,对破碎和聚结核函数的表达没有任何限制。
成核速率的定义方式与SMM相同。QMOM的生长速率由方程14.806(第808页)定义并表示为
14.9.2.3.4 直接矩量法(DQMOM)
DQMOM方程通过矩传递方法从基本数密度函数方程推导而来,类似于QMOM。不同之处在于,DQMOM假设每个积分点占据一个独立的流场,而QMOM假设所有积分点在同一流场中移动。这一差异使得DQMOM能够预测由于颗粒相互作用引起的颗粒分选。
在此DQMOM实现中,必须指定四个相:一个主相和三个次相,即DQMOM相。与QMOM相比,对于一个具有三个积分点的系统,DQMOM方法仅需要三个额外的方程来求解颗粒的有效长度,但每个DQMOM相的体积分数方程有额外的源项。在Ansys Fluent中,考虑了三种颗粒相互作用:生长、聚集和破碎。未考虑成核。
14.9.2.3.4.1 数值方法
描述一个经历聚集、破碎和生长的多分散颗粒系统的DQMOM方程可以写成如下形式(DQMOM公式的详细信息可以在[169](第1066页)中找到):
其中, 和 分别代表体积分数和颗粒相的有效长度。 表示单位体积内的颗粒数量,而 是在第 个积分点处的生长速率。至于 和 ,则可以通过使用 个积分点对颗粒数密度输运方程进行矩变换后得到的线性系统来计算。该线性系统可以用矩阵形式表示为
定义的 系数矩阵 如下:
未知向量 是一个由 个元素组成的向量,其定义如下:
方程14.822(第811页)右侧为仅涉及聚并和破碎现象的已知源项。生长项直接在方程14.820(第811页)和方程14.821(第811页)中考虑。目前,成核现象尚未纳入考虑。
第 阶矩的源项 定义为
当正交点 的横坐标不同时,矩阵 是良定义的,并且可以求得方程 14.822(第 811 页)的唯一解。否则,矩阵 不是满秩的,无法求逆以找到 的唯一解。Ansys Fluent 采用的解决方法是使用扰动技术。例如,对于当前的三个正交点系统,扰动技术会向横坐标添加一个小的值,以确保矩阵 是满秩的。需要注意的是,扰动技术仅用于矩阵 的定义,并未对公式 14.827(第 811 页)的源项向量进行任何修改。因此,由聚并和破碎产生的权重和总体源项均不受扰动方法的影响。模拟测试发现,扰动方法可以稳定公式 14.822(第 811 页)的解,并减少那些横坐标值过于接近的两相的物理上不切实际的巨大源项。然而,对于横坐标 与其他两相明显不同的相,该技术影响甚微。
14.9.2.4 群体平衡统计
以下部分介绍在使用群体平衡模型时有用的统计概念。
- 14.9.2.4.1 从矩重建颗粒尺寸分布
- 14.9.2.4.2 对数正态分布
14.9.2.4.1 从矩重建颗粒尺寸分布
给定一组矩,可以根据湍流火焰的“统计上最可能”分布 [529](第 1087 页)获得最可能的 PSD,该分布由 Baldyga 和 Orciuch [39](第 1059 页)针对结晶问题进行了调整。
数密度函数 表示为
第 阶矩的方程现表述为
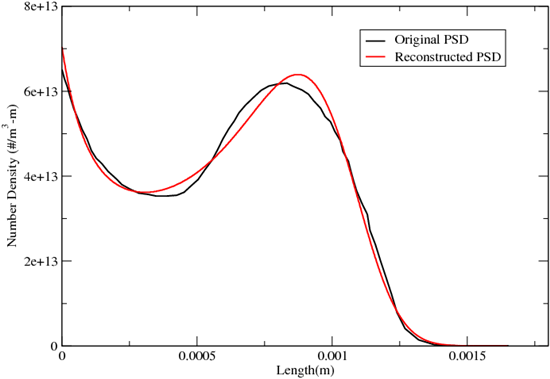
给定 个矩,可以通过全局收敛的牛顿-拉夫森方法找到系数 ,从而重建粒径分布(例如,图 14.22:粒径分布的重建(第 813 页))。
图 14.22:粒径分布的重建
14.9.2.4.2 对数正态分布
在使用任一种离散人口平衡方法时,您可以选择通过指定对数正态分布来设定速度进口处的尺寸分布。
粒径 作为变量的数量密度 的对数正态分布可以表示为:
其中, 和 分别是该分布的位置参数和尺度参数,可以表示为
和 分别为均值和标准差,并在初始化分仓分数时按对数正态分布的边界条件中给出,具体参见“初始化分仓分数时采用对数正态分布”部分。