以下章节介绍了预测的理论背景。关于在Fluent中使用模型的信息,请参阅用户指南中的“使用NOx模型”部分。
- 9.1.1. 概述
- 9.1.2. NOx传输的控制方程
- 9.1.3. 热力NOx的形成
- 9.1.4. 瞬发NOx的形成
- 9.1.5. 燃料NOx的形成
- 9.1.6. 由中间体N2O形成的NOx
- 9.1.7. 通过再燃减少NOx
- 9.1.8. 通过选择性非催化还原(SNCR)减少NOx
- 9.1.9. 湍流流动中的NOx形成
9.1.1 概述
排放主要由一氧化氮组成,较少程度上还包括二氧化氮和一氧化二氮。是光化学烟雾的前体物,对酸雨形成有贡献,并导致臭氧层损耗。因此,是一种污染物。Fluent的模型提供了一个工具,用以理解产生的来源,并辅助设计控制措施。
9.1.1.1 Fluent中的NOx建模
Fluent的模型具备模拟热力、瞬发和燃料形成的能力,以及由于再燃在燃烧系统中消耗的能力。它采用了英国利兹大学燃料与能源系开发的速率模型,以及来自公开文献的模型。通过试剂注入,如选择性非催化还原(SNCR)进行的减少,可以在Fluent中进行建模,同时还集成了一个中间体模型。
为了预测排放量,Fluent会求解一氧化氮(NO)浓度的传输方程。当存在燃料来源时,Fluent还会求解中间物种的额外传输方程。如果激活了中间模型,则会求解一个关于的附加传输方程。传输方程是基于给定的流动场和燃烧解决方案来求解的。换句话说,是从燃烧模拟中进行后处理的。因此,显而易见,准确的燃烧解决方案成为预测的前提条件。例如,当火焰温度约为时,每增加温度,热的生成量就会翻倍。必须非常小心地提供准确的燃烧模型热物理数据和边界条件输入。必须采用适当的湍流、化学、辐射及其他子模型。
要现实一点,你只能期待结果与输入数据和选定的物理模型一样准确。在大多数情况下,的变化趋势可以被准确预测,但的具体数量无法精确确定。准确预测参数趋势可以减少实验室测试的数量,允许研究更多的设计变化,缩短设计周期,并降低产品开发成本。这正是Fluent模型的力量所在,实际上也是CFD整体的力量所在。
9.1.1.2 火焰中的NOx形成与减少
在火焰中,的形成和减少是一个复杂的过程,涉及多种化学反应和物理机制。以下是一些关键点:
-
热形成:这是由于高温下氮气和氧气反应生成NO。火焰温度越高,热的生成量越大。
-
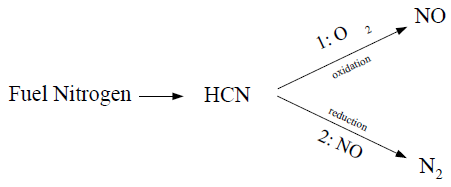
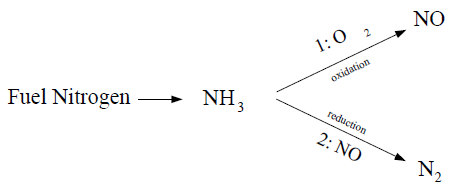
燃料形成:当燃料中含有氮元素时,这些氮元素会在燃烧过程中转化为NO。这通常涉及中间物种如HCN和NH3的反应。
-
快速形成:在富燃料条件下,碳氢化合物与氮气反应生成NO。
-
中间模型:是一种中间产物,可以进一步转化为NO。激活此模型可以更准确地模拟的形成过程。
-
减少机制:在某些条件下,火焰中的NO可以被还原为氮气。这通常涉及还原性物质如碳氢化合物和一氧化碳的反应。
为了准确模拟火焰中的形成和减少,需要考虑上述所有因素,并提供准确的输入数据和物理模型。Fluent提供了强大的工具来处理这些复杂性,从而帮助工程师优化燃烧过程,减少排放。
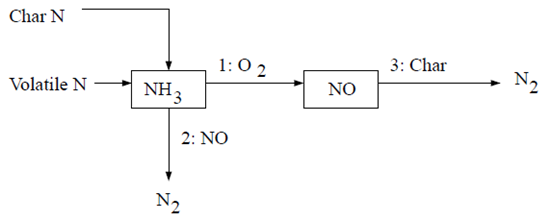
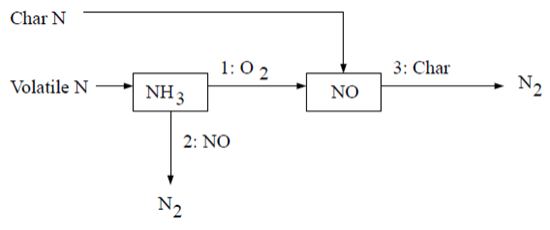
在层流火焰以及湍流火焰中的分子层面,的形成可归因于四种不同的化学动力学过程:热力形成、瞬时形成、燃料形成以及中间体。热力是由燃烧空气中存在的大气氮氧化而成。瞬时是在火焰前端的高速反应中产生。燃料则是由燃料中所含氮的氧化作用产生。在高压和富氧条件下,也可能通过分子氮经由形成。再燃和选择性非催化还原(SNCR)机制通过分别考虑NO与碳氢化合物和氨的反应,来减少总的生成。
重要提示:模型不能与预混燃烧模型同时使用。
9.1.2 NOx传输的控制方程
Fluent求解NO物种的质量传输方程,考虑了NO及相关物种的对流、扩散、生成和消耗。这种方法完全基于质量守恒的基本原理。在欧拉参考系中编写的控制方程中,通过对流项包含了机制中的停留时间效应(拉格朗日参考系概念)。对于热力和瞬时机制,仅需要NO物种的传输方程:
如《燃料NOx生成》(第371页)中所讨论的,燃料的生成机制更为复杂。追踪含氮中间物种的过程至关重要。Fluent除了求解物种的输运方程外,还会针对、或物种求解相应的输运方程:
其中,、、 和 分别表示气相中 、、 和 的质量分数,而 是有效扩散系数。接下来,我们将针对不同的 机理,确定源项 、、 和 。
9.1.3 热力型NOx的形成
热力型的形成由一组高度依赖温度的化学反应决定,这些反应被称为扩展Zeldovich机制。主导热力型从分子氮形成的主要是以下反应:
第三种反应已被证明有助于热力型的形成,特别是在近化学计量条件和富燃料混合物中:
9.1.3.1 热力型NOx反应速率
这些反应的速率常数已在众多实验研究中测量[68](第1060页),[186](第1067页),[450](第1083页),并且这些研究获得的数据已由Baulch等人[48](第1059页)和Hanson与Salimian [234](第1070页)进行了关键性评估。在模型中使用的方程9.5(第365页)- 方程9.7(第365页)的速率系数表达式如下所示。这些表达式是基于Hanson和Salimian [234](第1070页)的评估选择的。
在上面的表达式中,、和分别是正反应速率常数,对应于方程9.5(第365页)至方程9.7(第365页),而、和则是相应的逆反应速率常数。所有这些速率常数的单位均为m³/mol-s。
通过方程9.5(第365页)至方程9.7(第365页)中的反应生成NO的净速率为
所有浓度的单位均为 。
为了计算 和 的生成速率,需要 、 和 的浓度。
9.1.3.2 关于[N]的准稳态假设
的生成速率仅在高温(大于)下显著,因为固定氮需要打破强三键(提供941 kJ/mol的解离能)。这一效应通过反应方程式9.5(第365页)的高活化能表示,使其成为扩展Zeldovich机理的速率限制步骤。然而,原子氧化的活化能较小。当有足够的氧气时,如在贫燃火焰中,自由氮原子的消耗速率与其生成速率相等,因此可以建立准稳态。这一假设在大多数燃烧情况下有效,除非在极端富燃燃烧条件下。因此,NO的生成速率变为...
9.1.3.3 热力型NOx温度敏感性
从方程9.9(第366页)可以清楚地看出,NO的生成速率会随着氧气浓度的增加而增加。同时,热力型NO的形成似乎高度依赖于温度,但与燃料类型无关。事实上,根据由描述的极限速率,在超过的温度下,每增加,热力型的生成速率就会翻倍。
9.1.3.4 解耦热力型NOx计算
为了求解方程9.9(第366页),除了稳定物种(即)的浓度外,还需要O原子和自由基OH的浓度。根据Zeldovich的建议,可以通过假设温度、稳定物种、O原子和OH自由基的平衡值,将热力型的形成机制与主要燃烧过程解耦。然而,观察发现,自由基浓度(特别是O原子)比它们的平衡水平更为丰富。在层流甲烷-空气燃烧过程中,部分平衡O原子对形成速率的影响已被研究[445](第1082页)。这些研究结果表明,在假设平衡O原子浓度的情况下,火焰区域内的排放水平可能会被低估高达。
9.1.3.5 确定O原子浓度的方法
关于工业湍流火焰中自由基浓度的详细研究甚少,但已有研究[151](第1065页)证实了湍流扩散火焰中这一现象的存在。目前,关于部分平衡对湍流火焰中生成速率的影响尚无定论。Peters和Donnerhack [515](第1087页)提出,部分平衡自由基至多能导致热力型增加25%,而流体动力学对生成速率起主导作用。Bilger和Beck [60](第1060页)则认为,在湍流扩散火焰中,氧原子过量对生成速率的影响至关重要。
为克服这种潜在的不准确性,一种方法是将扩展的Zeldovich机理与包含众多反应、物种和步骤的详细烃类燃烧机理相结合。这种方法曾用于研究目的[440](第1082页)。然而,此类方法的高计算成本限制了它们在湍流反应流动中的应用。
为了确定氧自由基的浓度,Fluent提供了以下三种方法:平衡法、部分平衡法以及预测浓度法。
9.1.3.5.1 方法1:平衡法
热生成速率的动态过程远比主要碳氢化合物氧化速率缓慢,因此大部分热是在燃烧完成后形成的。因此,热的生成过程通常可以与主要燃烧反应机制解耦,并且可以通过假设燃烧反应达到平衡来计算的生成速率。采用这种方法,热生成速率的计算得到了显著简化。在较高火焰温度下,由于自由基过量的重要性降低,平衡假设得以成立[150](第1065页)。根据Westenberg[704](第1098页)的研究,平衡氧原子浓度可以通过以下表达式获得:
考虑到,该表达式变为
其中 以开尔文为单位。
9.1.3.5.2 方法2:部分平衡法
相较于方法1,我们可以通过考虑 解离-重组过程中的第三体反应来改进该方法:
于是,公式 9.11(第 367 页)被以下表达式所取代 [693](第 1097 页):
这通常会导致更高的部分氧原子浓度。
9.1.3.5.3 方法3:预测氧原子法
当使用高级化学模型(如非预混模型中的火焰子模型)能够很好地预测氧原子浓度时,[0]可以直接取自局部氧物种的质量分数。
9.1.3.6 确定OH自由基浓度的方法
Fluent采用三种方法之一来确定OH自由基浓度:从热力学NOx计算中排除OH,部分平衡法,以及使用预测的OH浓度。
9.1.3.6.1 方法1:排除OH法
在此方法中,通过以下观察,假设扩展Zeldovich机制中的第三个反应(公式9.7,第365页)可以忽略不计:
这种假设在贫燃料条件下是成立的,并且在大多数情况下也是一个合理的假设。
9.1.3.6.2 方法2:部分平衡法
在这种方法中,扩展Zeldovich机理中第三个反应(公式9.7,第365页)中的OH浓度由以下文献给出:[49](第1059页),[703](第1098页):
9.1.3.6.3 方法三:预测OH法
与预测法类似,当使用火焰面模型等高级化学模型能够很好地预测自由基浓度时,可以直接从局部物种的质量分数中获取。
9.1.3.7. 总结
总结来说,热力型的生成速率由公式9.9(第366页)预测。公式9.9(第366页)所需的氧原子浓度,在平衡假设下通过公式9.11(第367页)计算,在部分平衡假设下通过公式9.13(第367页)计算,或者直接使用局部氧物种的质量分数。您将在问题设置阶段做出选择。就NO的输运方程(公式9.1,第364页)而言,由于热力型机制产生的NO源项为
其中, 表示 NO 的分子量(单位:kg/mol),而 则根据方程 9.9(第 366 页)计算得出。
9.1.4 瞬时NOx生成
众所周知,在碳氢燃料的燃烧过程中, 的生成速率可能超过直接氧化氮分子(即热力型 )所产生的速率。
9.1.4.1 瞬时NOx的燃烧环境
导致 生成的第二种机制首先由 Fenimore [171](第1066页)识别出来,并被称为“瞬时 ”。有充分证据表明,在某些燃烧环境中,如低温、富燃料条件下以及停留时间较短的情况下,瞬时 可以大量形成。表面燃烧器、分级燃烧系统和燃气轮机都能创造这样的条件 [41](第1059页)。
目前,瞬时 对固定燃烧器总 的贡献较小。然而,随着采用新策略(燃烧器设计或炉膛几何形状的修改)将 排放降低到极低水平,瞬时 的相对重要性预计会增加。
9.1.4.2 瞬时NOx的生成机理
瞬时 在富燃火焰中最常见。其实际生成涉及一系列复杂的反应和多种可能的中间物种。目前公认的生成路径如下:
一些由燃料碎片产生的物种被认为是碳氢火焰中瞬时的来源(例如,、、、),但主要贡献来自于(见方程9.16,第369页)和。
这些反应的产物可能会导致胺类和氰化合物的形成,这些化合物随后通过类似于燃料氮氧化过程中发生的反应,进一步反应生成NO,例如:
9.1.4.3 瞬时NOx生成因素
瞬时的生成与单位体积内碳原子的数量成正比,且与母体烃的种类无关。HCN的生成量随烃自由基浓度的增加而增加,而烃自由基浓度又随当量比的增加而增加。随着当量比的增加,瞬时的产生首先增加,然后达到峰值,最后由于氧气的不足而减少。
9.1.4.4 主要反应
方程9.16(第369页)描述的反应至关重要。最近的研究[576](第1090页)表明,与峰值位置的概率密度分布相比,峰值位置的概率密度分布显示出紧密的对应关系,这表明火焰基部的大部分是通过反应生成的瞬时。假设方程9.16(第369页)描述的反应控制了瞬时的生成速率。
9.1.4.5 建模策略
然而,上述反应的速率数据存在不确定性。从方程9.16(第369页)至方程9.20(第369页)描述的反应中可以得出,预测火焰中瞬时的形成需要将动力学与实际的烃类燃烧机理相结合。烃类燃烧机理涉及许多步骤,如前所述,其计算极为复杂且成本高昂。在当前的模型中,采用了De Soete[139](第1065页)推导出的全局动力学参数。De Soete将总形成速率的实验值与通过数值积分计算出的和形成速率的经验总反应速率进行了比较。他表明,总体的瞬时形成速率可以通过以下表达式预测:
在火焰的初期阶段,在燃料富集条件下迅速形成时,氧浓度较高,氮自由基几乎仅形成而非氮气。因此,迅速的生成速率将大致等于整体迅速的生成速率:
对于乙烯()-空气火焰,
为 , 是氧反应级数, 是通用气体常数, 是压力(均采用 单位)。研究发现,瞬时 生成的速率对氮和燃料浓度是一级反应,但氧反应级数 取决于实验条件。
9.1.4.6 多数碳氢燃料的反应速率
方程 9.24(第 370 页)通过与 Backmier 等人 [35](第 1059 页)获得的实验数据对比进行了测试,涵盖了不同混合物和燃料类型。预测结果显示,在富燃料条件下和高碳氢燃料情况下,模型性能显著下降。为了减少这一误差并在所有条件下准确预测瞬时 ,利用现有实验数据对 De Soete 模型进行了修正。开发了一个修正因子 ,它考虑了燃料类型(即碳原子数)和气体烷烃的空气-燃料比的影响。方程 9.24(第 370 页)现在变为
从而使得由于瞬时机理产生的源项得以
在上述方程中,
(9.29)
为 303474.125 J/mol, 是烃燃料分子中碳原子的数量, 是当量比。修正因子是针对实验数据的曲线拟合,适用于脂肪烷烃类烃燃料 以及当量比在 0.6 到 1.6 之间的情况。对于超出此范围的值,应使用适当的极限值。 和 的值是在英国利兹大学燃料与能源系开发的。
此处,当量比的概念指的是火焰的整体当量比,而不是流动域中任何空间变化的量。在具有多个燃烧器的复杂几何结构中,这可能导致 的指定存在一些不确定性。然而,由于瞬时 对总 排放的贡献通常非常小,因此结果不太可能受到显著偏差。
9.1.4.7 氧反应级数
氧反应级数取决于火焰条件。根据 De Soete [139](第 1065 页),氧反应级数与火焰中的氧摩尔分数唯一相关:
9.1.5 燃料型NOx生成
9.1.5.1 燃料结合氮
众所周知,液体或固体化石燃料中含有的含氮有机化合物可以在燃烧过程中贡献总的形成。这种燃料氮对于残余燃料油和煤来说是一个特别重要的氮氧化物排放源,它们通常含有按重量计算的的氮。研究表明,重质燃料油中的大部分氮以杂环形式存在,并且认为煤中的氮组分与此类似[285](第1073页)。据信,吡啶、喹啉和胺类杂环结构是重要的。
9.1.5.2 反应途径
燃料氮转化为的程度取决于局部燃烧特性和氮结合化合物的初始浓度。当燃料液滴或颗粒在挥发阶段受热时,含氮的燃料结合化合物会释放到气相中。在反应区中,通过这些化合物(苯胺、吡啶、吡咯等)的热分解,可以形成、、、和等自由基,并转化为。上述自由基(即次级中间氮化合物)受到双重竞争反应路径的影响。这一化学机制已经
受到多次详细调查[441](第1082页)。尽管导致燃料形成和破坏的途径仍不完全清楚,但不同研究者似乎在简化的模型上达成了一致:

最近的调查[257](第1071页)显示,如果燃料氮以芳香或环状形式存在,氢氰酸似乎是主要产物。然而,当燃料氮以脂肪族胺的形式存在时,氨成为燃料氮转化的主要产物。
在Fluent的模型中,气态、液态和煤燃料的排放源分别考虑。含氮中间体被归类为、或两者的组合。在求解传输方程(方程9.1(第364页)和方程9.2(第365页)或方程9.3(第365页))后,确定了不同燃料类型的源项、和。以下讨论涉及燃料源项以及中间体和的源项和。热机制和瞬时机制的贡献已在前面章节中讨论。
9.1.5.3 气体和液体燃料的燃料NOx
气体和液体燃料的燃料机制基于不同的物理原理,但化学反应途径相同。
9.1.5.3.1 中间体氢氰酸(HCN)的燃料NOx
当HCN用作中间物种时:
传输方程中的源项可以写成如下形式:
9.1.5.3.1.1 气体燃料中的HCN生成
HCN的生成速率等同于燃料的燃烧速率:
其中
HCN 的源项
燃料的平均极限反应速率
燃料中氮的质量分数
燃料的平均极限反应速率 是根据 Magnussen 燃烧模型计算得出的,因此只有在使用广义有限速率模型时,气态燃料 选项才可用。
9.1.5.3.1.2 液态燃料中的 HCN 生成
HCN 的生成速率相当于通过液滴蒸发将燃料释放到气相中的速率:
其中:
HCN 的源项
液体滴流向气体释放燃料的速率
燃料中氮的质量分数
单元体积
9.1.5.3.1.3 HCN 消耗
上述机理中反应 (1) 和 (2) 对 HCN 的消耗速率,无论是气体燃料还是液体燃料,均相同,由 De Soete [139] (第 1065 页) 给出。
HCN 的转化率
瞬时温度 (K)
摩尔分数
氧反应级数 根据第 9.30 方程(第 371 页)计算得出。
由于摩尔分数与质量分数通过各组分 及混合物 的分子量相关联,
9.1.5.3.1.4 输运方程中的HCN来源
如方程9.31(第372页)所示,HCN的质量消耗率是按以下方式计算的。
, 反应1和反应2中HCN的消耗速率,单位分别为
压力(Pa)
平均温度(K)
普适气体常数
9.1.5.3.1.5 传输方程中的NOx来源
在反应1中生成,在反应2中被破坏。方程9.32(第373页)的来源
对于气体燃料和液体燃料是相同的,并且评估如下:
9.1.5.3.2 中间氨(NH3)产生的燃料NOx
当使用作为中间物种时:
传输方程中的源项可以写成如下形式:
9.1.5.3.2.1 气体燃料中NH3的生成
的生成速率等同于燃料的燃烧速率:
其中
氨源项
燃料的平均极限反应速率
燃料中氮的质量分数
燃料的平均极限反应速率 是根据 Magnussen 燃烧模型计算的,因此只有在使用广义有限速率模型时,气态燃料 选项才可用。
9.1.5.3.2.2 液态燃料中的 NH3 生成
的生成速率相当于通过液滴蒸发将燃料释放到气相中的速率:
其中
氨源项
从液滴释放到气体的燃料速率
燃料中氮的质量分数
单元体积
9.1.5.3.2.3 NH3 消耗
上述机理中反应 (1) 和 (2) 的 消耗速率对于气态和液态燃料是相同的,并由 De Soete [139] (p. 1065) 给出:
其中
氨的转化速率
瞬时温度 (K)
摩尔分数
氧反应级数 根据方程 9.30 (p. 371) 计算。
由于摩尔分数通过物种的分子量 和混合物的分子量 与质量分数相关, 可以使用方程 9.37 (p. 374) 计算。
9.1.5.3.2.4 输运方程中的 NH3 源项
方程 9.42 (p. 375) 中出现的 质量消耗速率计算为
其中
分别为反应1和反应2中的消耗速率
9.1.5.3.2.5 传输方程中的NOx来源
在反应1中生成,但在反应2中被破坏。方程9.43(第375页)的来源
对于气体燃料和液体燃料是相同的,并且评估如下:
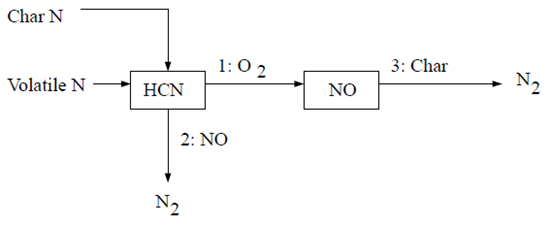
9.1.5.3.3 煤中的燃料NOx
9.1.5.3.3.1 焦炭和挥发物中的氮
对于煤,假设燃料氮分布在挥发物和焦炭之间。由于没有理由认为N在挥发物和焦炭之间均匀分布,因此应分别指定挥发物和焦炭中N的比例。
当使用作为中间物种时,包括了两种煤的燃料机制。当使用作为中间物种时,也包括了两种煤的燃料机制,类似于通过HCN计算煤的产生。假设燃料氮分布在挥发物和焦炭之间。
9.1.5.3.3.2 煤燃料NOx方案A
第一种HCN机制假设所有焦炭N转化为HCN,然后部分转化为NO [613](第1092页)。反应途径描述如下:
在第一种方案中,所有焦炭结合的氮转化为HCN。因此,
其中
炭烧失率
炭中氮的质量分数
单元体积
9.1.5.3.3.3 煤燃料NOx方案B
第二种HCN机理假设所有炭氮直接转化为NO [387](第1079页)。反应途径描述如下:
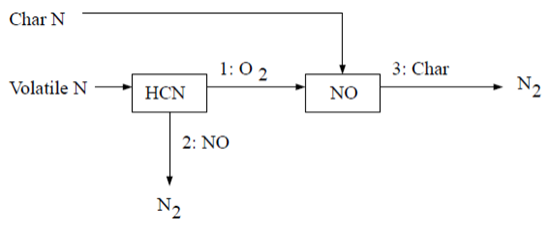
根据Lockwood [387](第1079页),炭氮直接以NO的形式释放到气相中,主要是作为氧化炭氮原子的解吸产物。如果采用这种方法,则
9.1.5.3.3.4 HCN方案选择
第二种HCN机制往往比第一种产生更多的排放。然而,通常很难说哪一种表现更优。
传输方程的源项为
、、 和 的来源已在先前描述。因此,只需考虑异相反应源 、焦炭 源 以及 HCN 生成源 。
9.1.5.3.3.5 焦炭表面 NOx 的还原
焦炭表面 NO 的异相还原反应已根据以下模型进行模拟 [360](第 1078 页):
其中
NO 还原速率
平均 NO 分压(atm)
平均温度(K)
分压 是使用道尔顿定律计算的:
由于反应3导致的NO消耗速率则为
BET 比表面积
颗粒浓度
NO 消耗量
9.1.5.3.3.5.1 BET 比表面积
涉及煤焦的非均相反应主要是一个吸附过程,其速率与孔隙表面积直接成正比。孔隙表面积也被称为 BET 比表面积,这一名称源自开创吸附理论的研究者(Brunauer, Emmett, 和 Teller [85] (p. 1061))。对于商用吸附剂,孔隙(BET)比表面积范围从 100,000 到 200 万 m²/kg,具体取决于微观结构。对于煤,BET 比表面积通常为 ,这在 Fluent 中作为默认值使用。总的 来源是挥发分贡献 和煤焦贡献 的组合:
9.1.5.3.3.5.2 挥发分中的 HCN
挥发分中 HCN 的来源与挥发分释放速率相关: 其中
从煤颗粒进入气相的挥发分源
挥发分中氮的质量分数
与煤焦结合氮相关的源项计算取决于燃料 方案的选择。
9.1.5.3.3.6 煤燃料 NOx 方案 C
第一种 机制假设所有煤焦 转化为 ,然后部分转化为 NO [613] (p. 1092)。反应路径描述如下:
在此方案中,所有煤焦结合氮转化为 。因此,
其中
煤粉燃尽速率
煤粉中氮的质量分数
单元体积
9.1.5.3.3.7 煤燃料NOx方案D
第二种机理假设所有煤粉中的氮直接转化为[387](第1079页)。反应途径描述如下:
根据Lockwood[387](第1079页),煤粉中的氮直接以NO的形式释放到气相中,主要是作为氧化煤粉氮原子的脱附产物。如果采用这种方法,则
9.1.5.3.3.8 氨方案选择
第二种机理往往比第一种产生更多的排放。然而,通常很难说哪一种表现更优。
传输方程的源项为
已知源贡献 、、、、 和 的描述。因此,只需考虑 的生产源 。
的整体生产源是挥发物贡献 和
焦炭贡献 的组合:
9.1.5.3.3.8.1 挥发物中的NH3
挥发物中 的来源与挥发物释放速率有关: 其中
从煤颗粒进入气相的挥发物源(kg/s)
挥发物中氮的质量分数
单元体积
与焦炭结合的氮相关的源的计算取决于燃料 方案的选择。
9.1.5.3.4 HCN和NH3中间体的燃料氮分配
在某些情况下,尤其是当燃料为固体时,在足够高的温度下 [472](第1084页), 和 都可以作为中间体生成。特别是,低阶(褐煤)煤已显示出比 水平高出10倍的 产量,而高阶(烟煤)煤仅显示出 HCN 的产量 [471](第1084页)。Winter 等人 [715](第1098页)的研究表明,对于烟煤,使用 分配比为 9:1 时,与仅指定单一中间物种相比, 预测结果更接近测量值。另一方面,Liu 和 Gibbs [386](第1079页)对木质生物质(松木片)的研究表明,由于燃料的较年轻年龄,建议的 比率为 1:9。
综上所述,上述工作强调了能够明确指出燃料氮的一部分将同时转化为和中间体的重要性。在Fluent中,每当或作为生成的中间体时,都可以使用燃料氮分配功能,尽管它主要适用于煤和生物质等固体燃料。和的反应路径和源项在之前的章节中已有描述。
9.1.6 通过中间体N2O形成的NOx
Melte和Pratt [426](第1081页)提出了第一个通过分子氮()经由一氧化二氮()形成的中间机制。氮气主要作为燃烧和稀释空气的组成部分进入燃烧系统。在有利的条件下,即高压和富氧条件下,这一中间机制可以贡献高达90%的燃烧过程中形成的。这使得它在燃气轮机和压缩点火发动机等工业应用中尤为重要。由于这些设备在越来越低的温度下运行以防止通过热机制形成,因此中间机制的相对重要性正在增加。据观察,在这些系统中形成的约30%的主要与中间机制有关。
中间体机制在无焰模式操作的系统中也可能具有重要性(例如,稀释燃烧、无焰燃烧、无焰氧化和FLOX系统)。在无焰模式下,燃料和氧气在惰性气体中高度稀释,使得燃烧反应和产生的热量释放发生在扩散区域。因此,避免了温度的急剧升高,从而防止了热力型的生成。研究表明,中间体机制可能贡献了无焰模式下形成的的约,其余部分可归因于快速型机制。通过多位研究者的间接观察和理论推测,已经认识到形成的相关性,这些研究涉及多种燃烧系统[40](第1059页),[122](第1064页),[207](第1068页),[632](第1093页),[641](第1094页)。
9.1.6.1 N2O - 中间体NOx机制
该机制的最简单形式[426](第1081页)考虑了两个可逆的基本反应:
在这里, 是一个通用的第三体。由于第一个反应涉及第三体,因此该机理在高压下更为有利。两个反应都涉及氧自由基 O,这使得该机理在富氧条件下更为有利。虽然并不总是合理,但通常假设自由基 O 原子仅来自分子氧的解离,
根据动力学速率定律,通过 中间体机理形成 的速率为
要解方程 9.68(第 382 页),您需要先计算 [O] 和 。
通常假设 处于准稳态(即 ),这意味着
方程 9.68(第 382 页)- 方程 9.69(第 382 页)的系统可以在已知 、 和 的浓度,方程 9.65(第 382 页)和方程 9.66(第 382 页)的动力学速率常数,以及方程 9.67(第 382 页)的平衡常数的情况下,求解 形成的速率。方程 9.66(第 382 页)中 NO 的出现意味着 机理与热 机理(以及其他 机理)的耦合。
在上面的表达式中,和分别是方程9.65(第382页)和方程9.66(第382页)的正向速率常数,而和是相应的逆向速率常数。、和的单位是,而的单位是。
9.1.7 NOx通过重燃减少
为公用锅炉设计复杂的燃烧系统,基于空气和燃料分级技术,涉及许多参数及其相互依赖性。这些参数包括局部化学计量比、温度和化学浓度场、停留时间分布、速度场和混合模式。成功应用炉内还原技术需要以最佳方式控制这些参数,以避免影响锅炉性能。在1990年代中期,描述分级燃烧系统再燃区NOx破坏动力学的全局模型开始出现。以下介绍其中两个模型。
9.1.7.1 瞬时方法
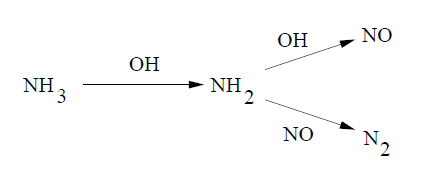
瞬时再燃机制是一种途径,通过该途径,与烃类反应并随后被还原。一般而言:
Fluent为模拟了三种再燃反应:
重要提示:如果温度超出此范围,NO reburn将不会被计算。
这些反应的速率常数取自Bowman [72](第1061页),单位为 /摩尔:
由于再燃导致的NO消耗速率可表示为:
在NO传输方程中,再燃机制的源项可以计算为:
重要提示:为了计算由于再燃导致的NO消耗速率,Fluent将从燃烧计算的物种质量分数结果中获取、和的浓度。使用此方法时,您必须确保在问题定义中包含物种、和。
9.1.7.2 部分平衡方法
部分平衡方法是基于Kandamby等人提出的模型[289](第1073页),[21](第1058页)。该模型在De Soete的全球模型[139](第1065页)中增加了一个还原路径,该模型描述了粉煤火焰中的形成/破坏机制。额外的还原路径考虑了在富燃料再燃区中通过自由基对的破坏(参见图9.1:带有额外还原路径的De Soete全球NOx机制(第384页))。
图9.1:带有额外还原路径的De Soete全球NOx机制
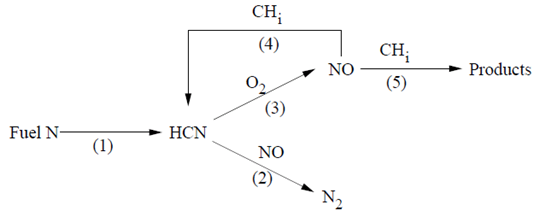
该模型可以与涡流耗散燃烧模型结合使用,并且不需要指定自由基浓度,因为它们是基于自由基的部分平衡计算的。再燃燃料本身可以是、、或的等效物。如何确定这种等效燃料尚有争议,一个近似的指导原则是考虑燃料本身的比。研究人员为再燃模型中的CH自由基部分平衡开发了一个乘积常数,以降低HCN和NO的速率。该值是通过预测一些存在实验数据的测试案例的值获得的。
9.1.7.2.1 NOx还原机制
在富燃料的再燃区,HCN的氧化受到抑制,而主燃烧区形成的NO量则通过从到的还原反应减少。然而,NO浓度也可能因与自由基的反应而降低,这些自由基在再燃区中有大量存在。以下被认为是通过自由基还原的最重要反应:
这些反应可以通过在图9.1中加入路径(4)和(5)来整体描述:De Soete的全球NOx机制,增加了还原路径(第384页),分别导致和次要中间氮自由基的形成。假设甲烷是再燃气体,那么全球NO还原速率可以表示为
在哪里
因此,由于再燃反应,HCN和NO输运方程的额外源项由以下公式给出:
为了评估速率常数 、 和 以及因子 和 ,需要做出某些假设。对于碳氢化合物扩散火焰,可以合理地认为以下反应集处于部分平衡状态:
因此,速率常数可以计算为
其中,、和是方程9.76(第385页)至方程9.78(第385页)的速率常数。方程9.83(第385页)至方程9.86(第385页)的正向和反向速率常数分别为至和至。此外,假设,因为在碳氢化合物扩散火焰的火焰后区域,H自由基的浓度已被观察到与的浓度处于同一数量级。最后,通过考虑反应 部分平衡,来估计自由基的浓度,从而得出关系式 不同等效燃料类型的速率常数、和的值以阿伦尼乌斯形式在表9.1:不同再燃燃料的速率常数(第386页)[357](第1077页)中给出。所有速率常数的单位为 /mol-s,所有值的单位为J/mol。
表9.1:不同再燃燃料的速率常数
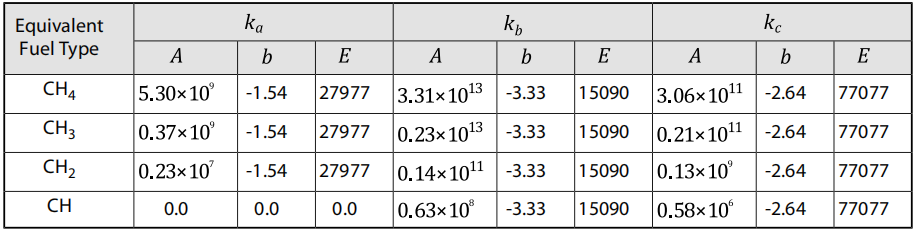
对于方程9.87(第386页),
9.1.8 SNCR脱硝技术
选择性非催化还原法(SNCR)是一种通过向炉内喷射选择性还原剂(如氨或尿素)来减少燃烧过程中排放的方法,该方法最早由Lyon [403](第1080页)描述。在炉内,这些还原剂能与烟气中的反应生成。然而,还原剂也可能被氧化形成。随着温度的升高,还原反应的选择性降低[439](第1082页),而引发反应的速率同时增加。这限制了SNCR过程只能在狭窄的温度区间内进行,即所谓的“温度窗口”,该区间的低温极限由停留时间决定。
9.1.8.1 氨喷射
多位研究者通过大量的基本反应对这一过程进行了建模。Fenimore [172](第1066页)基于实验测量提出了一种简单的经验模型,但该模型被发现不适用于实际应用。Ostberg和Dam-Johansen [501](第1086页)提出了一种两步方案,如图9.2所示:SNCR过程的简化反应机理(第387页),这是一个单一的引发步骤,随后是两个并行的反应路径:一个导致NO减少,另一个导致NO形成。
在4%体积氧气的条件下,Brouwer等人[82](第1061页)的工作估计了NO和NH₃的反应级数,以及方程9.88(第387页)和方程9.89(第387页)的经验速率常数kr和kox。研究发现,NO的反应级数对于方程9.88(第387页)为1,而NH₃的反应级数对于这两个反应均为1。因此,在4%体积氧气的条件下,针对NO和NH₃的反应速率提出了以下表达式:
速率常数 和 的单位是 ,它们被定义为
其中,,。
此模型已被证明能在煤粉燃烧和流化床燃烧应用中对SNCR过程做出合理的预测。该模型还能捕捉到对SNCR影响最大的参数,包括注入位置的烟气温度、在相关温度区间的停留时间、与的摩尔比以及可燃添加剂的影响。此模型在最佳温度以上对NO减少的过高估计量与Miller和Bowman的详细动力学模型[439](第1082页)相似。
重要提示:SNCR过程在火焰中存在作为燃料N中间体的时自然发生。因此,即使SNCR模型未激活且没有试剂注入,自然SNCR过程仍可能在火焰中发生。SNCR可能发生的温度范围或“窗口”为。如果您希望在不使用自然SNCR过程的情况下建模您的案例,请联系您的支持工程师以获取如何停用它的信息。
9.1.8.2 尿素注入
作为SNCR过程的试剂,尿素与注入氨类似,并已成功用于电站燃烧器以减少NO排放。然而,氨和尿素这两种试剂作为减少剂都有主要限制。有效性的狭窄温度“窗口”和混合限制是处理大型燃烧器时的难题。作为减少剂使用尿素而非氨的优势在于试剂的储存和处理更为简便。
使用尿素的SNCR过程结合了Thermal DeNOx(使用氨的SNCR)和RAPRENOx(使用氰尿酸的SNCR,在加热下升华并分解为异氰酸),因为尿素很可能分解为氨和异氰酸[439](第1082页)。
使用尿素的SNCR过程的一个问题是,HNCO的缓慢衰减以及导致和的反应途径,可能会显著增加除NO以外的污染物的排放。尿素似乎涉及大量含碳污染物的排放,如CO和HNCO。
此外,一些实验观察[560](第1089页)显示,与Thermal DeNOx过程相比,在还原剂中氮与进料中NO的比值相同的情况下,使用尿素的SNCR在较窄的温度窗口内有效,该窗口向更高温度偏移,其中定义为还原剂中氮与进料中NO的比值。增加值的效果是提高减排效率,而增加浓度的效果取决于温度。
这里描述的模型由Brouwer等人提出[82](第1061页),是一个七步简化动力学机制。Brouwer等人[82](第1061页)假设尿素的分解是瞬时的,并且1摩尔尿素产生1.1摩尔和0.9摩尔。Rota等人[560](第1089页)提出了一个有限速率的两步机制,用于尿素分解为氨和HNCO。
七步简化机制在表9.2中给出:使用尿素的SNCR的七步简化机制(第388页),两步尿素分解机制在表9.3中给出:两步尿素分解过程(第389页)。
表9.2:用于SNCR的七步简化机理与尿素
| Reaction | A | b | E |
|---|---|---|---|
| 4.24E+02 | 5.30 | 349937.06 | |
| 3.500E-01 | 7.65 | 524487.005 | |
| 2.400E+08 | 0.85 | 284637.8 | |
| 1.000E+07 | 0.00 | -1632.4815 | |
| 1.000E+07 | 0.00 | 0 | |
| 2.000E+06 | 0.00 | 41858.5 | |
| 6.900E+17 | -2.5 | 271075.646 |
表9.3:尿素的两步分解过程
| Reaction | A | b | E |
|---|---|---|---|
| 1.27E+04 | 0 | 65048.109 | |
| 6.13E+04 | 0 | 87819.133 |
其中,表9.2:用于SNCR的七步简化机理与尿素(第388页)和表9.3:尿素的两步分解过程(第389页)使用了国际单位制。
9.1.8.3 尿素、HNCO和NCO的传输方程
当采用尿素喷射的SNCR模型时,除了常规的传输方程外,Fluent还求解以下三个关于尿素、HNCO和NCO物种的额外质量传输方程。
其中, 和 分别表示气相中尿素、HNCO 和 NCO 的质量分数。源项 和 根据表 9.2:SNCR 七步简化机理(第 388 页)和表 9.3:尿素两步分解过程(第 389 页)中给出的速率方程以及由于试剂注入产生的额外源项来确定。这些额外源项将在下文进行确定。输运方程中的源项可以写成如下形式:
除了上述三种物种的源项外,还需要确定 、 和 的额外源项,具体如下,这些源项应添加到先前由于燃料 计算的源项中:
第 种物质的源项 由表 9.2 和表 9.3 中的速率方程确定:
- 表 9.2:SNCR 与尿素的七步简化机理(第 388 页)
- 表 9.3:尿素分解的两步过程(第 389 页)
9.1.8.4 由于试剂喷射导致的尿素生成
尿素生成速率等同于试剂通过液滴蒸发释放到气相中的速率: 其中, 是试剂从液滴释放到气相中的速率(kg/s), 是单元体积(m³)。
9.1.8.5 由于试剂喷射导致的 NH3 生成
如果尿素分解模型设置为用户指定选项,则 NH3 生成速率与试剂通过液滴蒸发释放到气相中的速率成正比: 其中, 是试剂从液滴释放到气相中的速率(kg/s), 是尿素分解产生的 NH3/HNCO 混合物中 NH3 的摩尔分数, 是单元体积(m³)。
9.1.8.6 由于试剂喷射导致的 HNCO 生成
如果尿素分解模型设置为用户指定选项,则 HNCO 生成速率与试剂通过液滴蒸发释放到气相中的速率成正比: 其中, 是试剂从液滴释放到气相中的速率(kg/s), 是尿素分解产生的 NH3/HNCO 混合物中 HNCO 的摩尔分数, 是单元体积(m³)。
重要提示:氨和异氰酸(HNCO)的摩尔转换分数(MCF)是通过用户指定的物种值确定的,例如,如果一摩尔尿素分解成1.1摩尔氨和0.9摩尔异氰酸,那么MCF_NH3 = 0.55,MCF_HNCO = 0.45。当使用用户指定的尿素分解选项时,S_pl,CO(NH2)2 = 0。
然而,尿素分解的默认选项是通过表9.3(第389页)中给出的限速反应的两步尿素分解过程进行的,相应的源项也据此计算。在这种情况下,S_pl,NH3和S_pl,HNCO的值均为零。
9.1.9 湍流中的NOx生成
前述关于NOx生成和破坏的动力学机制均来自实验室实验,使用层流预混火焰或冲击管研究,其中分子扩散条件定义明确。然而,在任何实际燃烧系统中,流动都是高度湍流的。湍流混合过程导致温度和物种浓度随时间波动,这将影响火焰的特性。
NOx生成速率、温度和物种浓度之间的关系高度非线性。因此,如果在任何模型中使用时间平均的组成和温度来预测平均NOx生成速率,将会产生显著误差。必须通过考虑描述时间变化的概率密度函数来考虑温度和组成的波动。
9.1.9.1 湍流-化学相互作用模型
在湍流燃烧计算中,Fluent求解密度加权时间平均的Navier-Stokes方程,用于温度、速度和物种浓度或平均混合分数和方差。为了计算NO浓度,必须在域中的每个点使用平均流动场信息计算时间平均的NO生成速率。
模拟平均湍流反应率的方法可以基于矩方法[714](第1098页)或概率密度函数(PDF)技术[279](第1073页)。Fluent采用PDF方法。
重要提示:此处描述的PDF方法仅适用于传输方程。前述的燃烧模拟可以使用Magnussen和Hjertager的广义有限速率化学模型、非预混或部分预混燃烧模型。有关这些模型的详细信息,请参阅物种传输和有限速率化学(第237页)、非预混燃烧(第295页)和部分预混燃烧(第343页)。
9.1.9.2 PDF方法
PDF方法在湍流流动的理论描述中已被证明非常有用[280](第1073页)。在Fluent的模型中,使用关于归一化温度、物种质量分数或两者的组合的单变量或联合变量PDF来预测排放。如果使用非预混或部分预混燃烧模型来模拟燃烧,则还可以使用关于混合分数的一变量或两变量PDF。构建PDF所需的独立变量的平均值是从传输方程的解中获得的。
9.1.9.3 平均反应率的一般表达式
平均湍流反应率可以用瞬时反应率和各种变量的单变量或联合PDF来描述。一般而言,
其中是温度和/或存在的各种物种浓度。是概率密度函数(PDF)。
9.1.9.4 Fluent中使用的平均反应率
PDF 用于对 NO 的瞬时生成速率(例如,公式 9.15(第 368 页))进行加权,并在适当范围内进行积分以获得平均湍流反应速率。因此我们有
或者,对于两个变量
其中 是 的平均湍流生成速率, 是 NO 的瞬时摩尔生成速率, 是瞬时密度,而 和 是变量 以及相关情况下 的概率密度函数(PDF)。对于 或 的源项,同样适用此处理方法。
公式 9.105(第 392 页)或公式 9.106(第 392 页)必须在每个节点和每次迭代时进行积分。对于以温度为变量的 PDF,积分的上下限由燃烧解中的温度最小值和最大值决定(注意,最大温度的计算有几种选项,如用户指南中设置湍流参数所述)。对于以混合分数为变量的 PDF,公式 9.105(第 392 页)或公式 9.106(第 392 页)中的积分限由查找表中的值确定。
9.1.9.5 统计独立性
在双变量 PDF 的情况下,进一步假设变量 和 是统计独立的,因此 可以表示为
9.1.9.6 Beta PDF 选项
Fluent 可以将 视为适用于燃烧计算的二阶 beta 函数 [231](第 1070 页),[444](第 1082 页)。beta 函数的方程为 其中 是 Gamma 函数,而 和 取决于所讨论数量的平均值 及其方差 :
Beta 函数要求独立变量 的取值范围在 0 到 1 之间。因此,诸如温度之类的场变量必须进行归一化处理。有关在使用单混合分数模型和双混合分数模型时如何使用 Beta PDF 的信息,请参阅用户指南中的“设置湍流参数”部分。
9.1.9.7 高斯 PDF 选项
Fluent 还可以假设 呈现出在尾部带有 delta 函数的截断高斯形式。
高斯 PDF 的累积密度函数 可以用误差函数表示如下:
其中 是误差函数, 是感兴趣的量, 和 分别是 的均值和方差。误差函数可以用不完全伽马函数 表示:
9.1.9.8 方差计算方法
场变量(温度和物种质量分数)的方差 可以在燃烧计算或污染物后处理阶段通过求解以下输运方程来计算: 其中常数 和 分别取值 和 2.0。
需要注意的是,上述方差输运方程仅用于温度方差的计算。求解额外的方程可能在计算上较为耗时,因此对于 预测的后处理处理来说,可能并不是首选方案。
除了方差输运方程外,Fluent 还提供了一种代数方法来计算 。这是一种近似方法,假设方差的生产和耗散相等,具体如下: 方括号中的项是独立变量的耗散率。当代数方法用于构建包含多个变量(如方程 9.107(第 392 页)中的温度-物种 PDF)的 PDF 时,代数方法是首选。当湍流化学相互作用模式为温度-物种时,物种方差通过代数方法计算,而温度方差可以通过代数方法或使用输运方程来计算。
对于以混合分数为变量的 PDF,混合分数方差已经作为基本燃烧计算的一部分进行了求解,因此无需额外计算 。