在非预混燃烧中，燃料和氧化剂以不同的流进入反应区。这与预混系统形成对比，预混系统中反应物在燃烧前已在分子层面混合。非预混燃烧的例子包括粉煤炉、柴油内燃机和池火。

在某些假设下，热化学可以简化为一个单一参数：混合分数。混合分数，记作 $f$，是源自燃料流的物质质量分数。换句话说，它是在所有组分中（如 $({\mathrm{CO}}_2,{\mathrm{H}}_2\mathrm{O},{\mathrm{O}}_2$ 等）燃烧和未燃烧的燃料流元素（C、H 等）的局部质量分数。这种方法优雅之处在于化学反应中元素是守恒的。因此，混合分数是一个守恒的标量量，其控制输运方程没有源项。燃烧简化为混合问题，避免了闭合非线性平均反应速率的困难。一旦混合，化学反应可以被建模为化学平衡状态，使用平衡模型；接近化学平衡状态，使用稳态扩散小火焰模型；或显著偏离化学平衡状态，使用非稳态扩散小火焰模型。

更多关于使用非预混燃烧模型的信息，请参阅用户指南中的“建模非预混燃烧”部分。非预混燃烧模型的理论信息将在以下章节中介绍：

• 8.1.1. 简介
• 8.1.2. 非预混燃烧与混合分数理论
• 8.1.3. 使用非预混模型时的限制与特殊情况
• 8.1.4. 扩散小火焰模型理论
• 8.1.5. 稳态扩散小火焰模型理论
• 8.1.6. 非稳态扩散小火焰模型理论

8.1.1 简介

非预混模型涉及求解一个或两个守恒标量（混合分数）的输运方程。不直接求解单个组分的方程，而是从预测的混合分数场中推导出组分浓度。热化学计算预处理后，在Ansys Fluent中以表格形式供查询。湍流与化学反应的相互作用通过假设形状的概率密度函数（PDF）来考虑。

8.1.2 非预混燃烧与混合分数理论

以下部分介绍了非预混燃烧和混合分数理论的相关信息：

• 8.1.2.1. 混合分数理论
• 8.1.2.2. 湍流-化学相互作用模型
• 8.1.2.3. 非预混模型的非绝热扩展
• 8.1.2.4. 化学反应表格化

8.1.2.1 混合分数理论

8.1.2.1.1 混合分数的定义

非预混模型方法的基础是，在一定简化假设下，流体的瞬时热化学状态与一个称为混合分数的守恒标量有关，记为$f$。混合分数可以用原子质量分数表示为[601]（第1092页）：

$$f=\frac{Z_i-Z_{i,ox}}{Z_{i,\text{ fuel }}-Z_{i,ox}}\text{\hspace{1em}(8.1)}$$

其中，$Z_i$ 表示元素 $i$ 的元素质量分数。下标 ox 表示氧化剂流入口处的值，下标 fuel 表示燃料流入口处的值。如果所有组分的扩散系数都相等，那么对于所有元素，方程 8.1（第 296 页）都是相同的，混合分数的定义也是唯一的。因此，混合分数就是源自燃料流的元素质量分数。

如果包含次级流（另一种燃料或氧化剂，或非反应流），则燃料和次级混合分数分别简单地表示燃料流和次级流的元素质量分数。系统中所有三个混合分数（燃料、次级流和氧化剂）的总和始终等于 1：

$$f_{\text{fuel }}+f_{\text{sec }}+f_{\text{ox }}=1\text{\hspace{1em}(8.2)}$$

这表明，在混合分数空间中，只有位于平面ABC上的点是有效的（如图8.1：混合分数关系（燃料、次级流和氧化剂）（第297页）所示）。因此，两个混合分数$f_{\text{fuel}}$和$f_{\text{sec}}$不能独立变化；它们的值只有在图8.1：混合分数关系（燃料、次级流和氧化剂）（第297页）所示的三角形OBC内时才有效。

图8.1：混合分数关系（燃料、次级流和氧化剂）

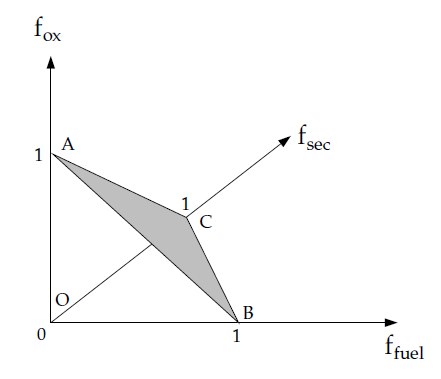
图8.2：混合分数关系（燃料、次级流和归一化次级混合分数）

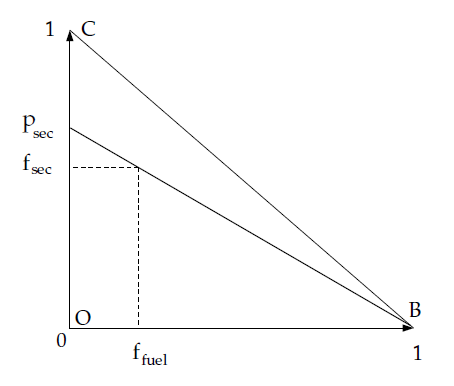
Ansys Fluent将三角形OBC离散化，如图8.2：混合分数关系（燃料、次级流和归一化次级混合分数）（第297页）所示。本质上，主混合分数$f_{\text{fuel}}$允许在零到一之间变化，如同单混合分数情况，而次级混合分数则位于具有以下方程的直线上：

$$f_{\text{sec }}=p_{\text{sec }}\times \left(1-f_{\text{fuel }}\right)\text{\hspace{1em}(8.3)}$$

其中，$p_{sec}$ 是归一化的次级混合分数，表示在次级混合分数轴上某直线交点的值。需要注意的是，与 $f_{sec}$ 不同，$p_{sec}$ 的取值范围始终在零和一之间，不受 $f_{\text{fuel }}$ 值的影响。

归一化次级混合分数 $p_{sec}$ 的一个重要特性是它假定与燃料混合分数 $f_{\text{fuel }}$ 统计独立。请注意，与 $f_{\text{sec }}$ 不同，$p_{\text{sec }}$ 不是一个守恒标量。这种归一化的混合分数定义 $p_{sec}$，在 Ansys Fluent 中提示次级混合分数时被普遍使用，除非在定义次级燃料流的富限时，此时使用的是 $f_{sec}$。

8.1.2.1.2 混合分数的输运方程

在假设各组分扩散系数相等的情况下，组分方程可以简化为一个关于混合分数 $f$ 的方程。由于化学反应中元素守恒，组分方程中的反应源项相互抵消，因此 $f$ 是一个守恒量。尽管对于层流流动，等扩散系数假设存在问题，但对于湍流流动而言，通常是可接受的，因为在湍流中湍流对流远超过分子扩散。Favre 平均（密度加权平均）的混合分数方程为：

$$\frac{\partial }{\partial t}\left(\rho \bar{f}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\bar{f}\right)=\nabla \cdot \left(\left(\frac{k_l}{C_p}+\frac{{\mu }_t}{{\sigma }_t}\right)\nabla \bar{f}\right)+S_m+S_{\text{user }}\text{\hspace{1em}(8.4)}$$

其中，$k_l$ 是混合物的层流热导率，$C_p$ 是混合物的比热容，${\sigma }_t$ 是普朗特数，${\mu }_t$ 是湍流粘度，$S_m$ 是由于液体燃料液滴或反应颗粒（例如煤）向气相转移质量而产生的源项，$S_{\text{user }}$ 是用户定义的任何源项。

除了求解Favre平均混合分数外，Ansys Fluent还求解混合分数方差的守恒方程，$\overline{f^{\prime 2}}$ [283]（第1073页）：

$$\frac{\partial }{\partial t}\left(\rho \overline{f^2}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overline{f^2}\right)=\nabla \cdot \left(\left(\frac{k_l}{C_p}+\frac{{\mu }_t}{{\sigma }_t}\right)\nabla \overline{f^2}\right)+C_g{\mu }_t\cdot {\left(\nabla \overline{f}\right)}^2-C_d\rho \frac{\epsilon }{k}\overline{f^2}+S_{user}\text{\hspace{1em}(8.5)}$$

其中，$k$ 表示湍流动能，而 $f^{\prime }=f-\bar{f}$。常数 ${\sigma }_t$、$C_g$ 和 $C_d$ 的默认值分别为 $0.85$、$2.86$ 和 2.0。

混合分数方差用于描述湍流-化学相互作用的封闭模型中（参见湍流-化学相互作用建模（第301页））。

对于双混合分数问题，$\overline{f_{\text{fuel }}}$ 和 $\overline{f_{\text{fuel }}^{\prime 2}}$ 是通过将 $\overline{f_{\text{fuel }}}$ 替换为 $\bar{f}$ 并将 $\overline{f_{\text{fuel }}^{{}^{\prime }2}}$ 替换为 $\overline{f^{{}^{\prime }2}}$ 从方程8.4（第298页）和方程8.5（第298页）中获得的。$\overline{f_{\text{sec }}}$ 是通过将 $\overline{f_{sec}}$ 替换为 $\bar{f}$ 从方程8.4（第298页）中获得的。然后使用方程8.3（第298页）计算 $\overline{p_{sec}}$，并通过将 $\overline{p_{sec}}$ 替换为 $\bar{f}$ 求解方程8.5（第298页）来获得 $\overline{p_{sec}^{\prime 2}}$。在第一近似中，$\overline{p_{sec}}$ 和 $\overline{f_{sec}}$ 的方差对 $\overline{f_{fuel}}$ 相对不敏感，因此 $\overline{p_{sec}^{\prime 2}}$ 的方程基本上与 $\overline{f_{sec}^{\prime 2}}$ 相同。

重要提示：当次级流的流量相对于总流量较小时，$\overline{p_{sec}^{\prime 2}}$ 而不是 $\overline{f_{sec}^{\prime 2}}$ 的方程是有效的。

8.1.2.1.3 LES 的非预混模型

对于大涡模拟，不针对混合分数方差求解输运方程，而是将其建模为...

$$\overline{f^{\prime 2}}=C_{\text{var }}{L}_s^2{\left|\nabla \bar{f}\right|}^2\text{\hspace{1em}(8.6)}$$

其中

$C_{\text{var }}=$ 常数

$L_s=$ 亚网格长度尺度（参见公式 4.307 (第121页)）

常数 $C_{var}$ 在粘性对话框中启用动态应力选项时会动态计算，否则使用固定值（默认值为0.5）。

如果启用了动态标量通量选项，湍流Sc $({\sigma }_t$ 在公式 8.4 (第298页)中) 会动态计算。

8.1.2.1.4 结合 SBES 湍流模型的非预混模型

在使用 SBES 湍流模型时，域中存在明显可辨的 RANS 和 LES 区域。当从 RANS 过渡到 LES 或反之时，使用公式 8.5 (第298页) 计算的 RANS 公式中的混合分数方差和使用公式 8.6 (第299页) 建模的 LES 公式中的混合分数方差不会恢复相同的行为。为了确保 RANS 和 LES 模型之间的过渡一致，在 RANS 区域使用混合分数方差的输运方程，而在 LES 区域使用代数公式。两者的混合方式与湍流粘度（公式 4.297 (第117页)）相同。SBES 的混合分数方差建模如下：

$$\overline{f^{\prime 2}}=\overline{f_{RANS}^{\prime 2}}{f}_{SDES}+\left(1-f_{SDES}\right)\overline{f_{LES}^{\prime 2}}\text{\hspace{1em}(8.7)}$$

8.1.2.1.5 混合分数与当量比

混合分数的定义可以与反应系统的常见度量联系起来理解。考虑一个简单的燃烧系统，涉及燃料流（F）、氧化剂流（O）和产物流（P），在化学计量条件下符号化表示为

$$F+rO\to \left(1+r\right)P\text{\hspace{1em}(8.8)}$$

其中，$r$ 是以质量为基础的空气与燃料比。将当量比表示为 $\varphi$，其中

$$\varphi =\frac{{\left(\text{ fuel }/\text{ air }\right)}_{\text{actual }}}{{\left(\text{ fuel }/\text{ air }\right)}_{\text{stoichiometric }}}\text{\hspace{1em}(8.9)}$$

在更普遍的混合条件下，方程8.8（第299页）中的反应可以表示为：

$$\varphi F+rO\to \left(\varphi +r\right)P\text{\hspace{1em}(8.10)}$$

观察该方程的左侧，我们可以推断出整个系统的混合分数为

$$f=\frac{\varphi }{\varphi +r}\text{\hspace{1em}(8.11)}$$

方程8.11（第300页）允许在化学计量条件下（$\varphi =1$）或富燃料条件下（例如，$\varphi >1$），或贫燃料条件下（例如，$\varphi <1$）计算混合分数。

8.1.2.1.6 混合分数与组分质量分数、密度和温度的关系

混合分数建模方法的优势在于，化学反应被简化为一个或两个守恒的混合分数。在化学平衡假设下，所有热化学标量（组分分数、密度和温度）都与混合分数唯一相关。

对于绝热系统中的单一混合分数，质量分数、密度和温度的瞬时值仅取决于瞬时混合分数$f$：

$${\varphi }_i={\varphi }_i\left(f\right)\text{\hspace{1em}(8.12)}$$

若包含次级流，瞬时值将取决于瞬时燃料混合分数 $f_{\text{fuel }}$ 以及次级部分分数 $p_{sec}$：

$${\varphi }_i={\varphi }_i\left(f_{\text{fuel }},p_{\text{sec }}\right)\text{\hspace{1em}(8.13)}$$

在公式8.12（第300页）和公式8.13（第300页）中，${\varphi }_i$ 表示瞬时的组分质量分数、密度或温度。对于非绝热系统，热量的损失/增益效应被参数化处理。

$${\varphi }_i={\varphi }_i\left(f,H\right)\text{\hspace{1em}(8.14)}$$

对于单一混合分数系统，其中 $H$ 表示瞬时焓（见方程 5.8，第 173 页）。

如果包含次级流，

$${\varphi }_i={\varphi }_i\left(f_{\text{fuel }},p_{\text{sec }},H\right)\text{\hspace{1em}(8.15)}$$

非绝热流动的例子包括存在辐射的系统、通过壁面的热传递、向/从离散相粒子或液滴的热传递，以及具有不同温度的多个入口。

关于这类非绝热系统中混合分数方法的更多细节，请参阅《非绝热扩展的非预混模型》（第305页）。

在许多反应系统中，燃烧并不处于化学平衡状态。Ansys Fluent提供了几种模拟化学非平衡的方法，包括有限速率法（参见《反应建模的广义有限速率公式》（第243页））、EDC（参见《涡耗散概念（EDC）模型》（第249页））和PDF输运（参见《成分PDF输运》（第276页））模型，这些模型可以结合详细的化学动力学机制。

在非预混燃烧模型中，有三种方法模拟化学非平衡。第一种是使用平衡模型中的富燃极限（RFL）选项，其中富区被模拟为纯燃料和较贫的平衡燃烧混合物的混合但未燃烧的混合物（参见《用户指南》中的启用富燃极限（RFL）选项）。第二种方法是稳态扩散小火焰模型，其中可以模拟由于湍流引起的扩散小火焰拉伸导致的化学非平衡。第三种方法是瞬态扩散小火焰模型，其中可以模拟远离化学平衡的缓慢形成的产品组分。有关Ansys Fluent中稳态和瞬态扩散小火焰模型的详细信息，请参阅《扩散小火焰模型理论》（第319页）和《瞬态扩散小火焰模型理论》（第327页）。

8.1.2.2 湍流-化学相互作用的建模

方程8.12（第300页）至方程8.15（第300页）描述了在化学平衡假设下，混合分数与组分分数、密度和温度之间的瞬时关系。然而，Ansys Fluent对湍流反应流的预测关注的是这些波动标量的平均值的预测。这些平均值与瞬时值之间的关系取决于湍流-化学相互作用模型。当使用非预混模型时，Ansys Fluent采用假设形状的概率密度函数（PDF）方法作为其封闭模型。本节将描述假设形状PDF封闭模型。

8.1.2.2.1 概率密度函数的描述

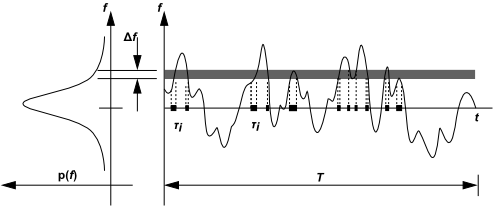
概率密度函数，记作 $p\left(f\right)$，可以理解为流体在状态 $f$ 附近花费的时间比例。图8.3：概率密度函数的图形描述（第302页）绘制了流场中某点混合分数的时间轨迹（右侧）以及 $f$ 的概率密度函数（左侧）。图中右侧绘制的 $f$ 的波动值在标记为 $\Delta f$ 的范围内花费了一定比例的时间。左侧绘制的 $p\left(f\right)$ 取值使得在其曲线下的带状区域 $\Delta f$ 内的面积等于 $f$ 在该范围内花费的时间比例。用数学表达式表示为：

$$p\left(f\right)\Delta f=\underset{T\to \infty }{\lim }\frac{1}{T}\sum _i{\tau }_i\text{\hspace{1em}(8.16)}$$

其中，$T$ 是时间尺度，${\tau }_i$ 是 $f$ 在 $\Delta f$ 频带内所花费的时间。函数 $p\left(f\right)$ 的形状取决于 $f$ 中湍流波动的性质。实际上，$p\left(f\right)$ 是未知的，通常被建模为一个数学函数，该函数近似于实验观察到的实际概率密度函数（PDF）形状。

图 8.3：概率密度函数的图形描述

8.1.2.2.2 从瞬时混合分数推导平均标量值

描述湍流流动中 $f$ 时间波动的概率密度函数 $p\left(f\right)$，可用于计算依赖于 $f$ 的变量的平均值。在绝热系统中，可以计算密度加权平均的组分质量分数和温度，如下所示：

$${\bar{\varphi }}_i={\int }_0^{1}p\left(f\right){\varphi }_i\left(f\right)df\text{\hspace{1em}(8.17)}$$

针对单一混合分数系统。当存在次级流时，平均值的计算方式如下：

$${\bar{\varphi }}_i={\int }_0^1{\int }_0^1{p}_1\left(f_{\text{fuel }}\right)p_2\left(p_{\text{sec }}\right){\varphi }_i\left(f_{\text{fuel }},p_{\text{sec }}\right)d{f}_{\text{fuel }}d{p}_{\text{sec }}\text{\hspace{1em}(8.18)}$$

其中，$p_1$ 表示 $f_{\text{fuel }}$ 的概率密度函数（PDF），而 $p_2$ 则是 $p_{\text{sec }}$ 的PDF。在此，假定 $f_{\text{fuel }}$ 和 $p_{\text{sec}}$ 统计独立，因此有 $p\left(f_{\text{fuel }},p_{\text{sec}}\right)=p_1\left(f_{\text{fuel }}\right)p_2\left(p_{\text{sec}}\right)$。

同样地，平均时间平均流体密度 $\bar{\rho }$ 也可以计算得到。

$$\frac{1}{\bar{\rho }}={\int }_0^1\frac{p\left(f\right)}{\rho \left(f\right)}df\text{\hspace{1em}(8.19)}$$

对于单一混合分数系统，以及

$$\frac{1}{\bar{\rho }}={\int }_0^1{\int }_0^1\frac{p_1\left(f_{\text{fuel }}\right)p_2\left(p_{\text{sec }}\right)}{\rho \left(f_{\text{fuel }},p_{\text{sec }}\right)}d{f}_{\text{fuel }}d{p}_{\text{sec }}\text{\hspace{1em}(8.20)}$$

当存在次级流时，$\rho \left(f\right)$ 或 $\rho \left(f_{\text{fuel }},p_{\text{sec }}\right)$ 是利用理想气体定律方程中的瞬时组分质量分数和温度获得的瞬时密度。使用方程 8.17（第 302 页）和方程 8.19（第 302 页）（或方程 8.18（第 302 页）和方程 8.20（第 302 页）），只需指定函数 $p\left(f\right)$（或 $p_1\left(f_{\text{fuel }}\right)$ 和 $p_2\left(p_{sec}\right)$ ）的形状，即可确定流场中所有点的局部平均流体状态。

8.1.2.2.3 假设形状的概率密度函数（PDF）

假设的概率密度函数 $p\left(f\right)$ 的形状由 Ansys Fluent 中的两种数学函数之一描述：

• 双δ函数（仅适用于双混合分数情况）
• β函数（适用于单混合分数和双混合分数情况）

双δ函数是最容易计算的，而β函数最接近实验观察到的概率密度函数。该函数产生的形状仅取决于混合分数的平均值 $\bar{f}$ 及其方差 $\overline{f^{{}^{\prime }2}}$。以下是对每种函数的详细描述。

8.1.2.2.3.1 双δ函数概率密度函数

双δ函数定义为

$$p\left(f\right)=\{\begin{array}{cc}0.5,& f=\bar{f}-\sqrt{f^{{}^{\prime }2}}\\ 0.5,& f=\bar{f}+\sqrt{f^{{}^{\prime }2}}\\ 0,& \text{ elsewhere }\end{array}\text{\hspace{1em}(8.21)}$$

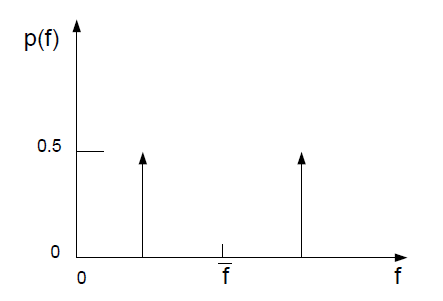
在 $f=1$ 和 $f=0$ 附近进行适当的边界限制。双δ函数的一个例子如图 8.4 所示：双δ函数PDF形状示例（第304页）。如上所述，双δ函数PDF非常易于计算，但由于它假设湍流流动中只存在两种状态，因此其准确性总是低于替代的β函数PDF。因此，它仅适用于两种混合分数的模拟，因为在这种情况下，计算成本的节省是显著的。

图 8.4：双δ函数PDF形状示例

8.1.2.2.3.2 β函数PDF

β函数PDF形状由以下关于 $\overline{f}$ 和 $\overline{f^{{}^{\prime }2}}$ 的函数给出：

$$p\left(f\right)=\frac{f^{\alpha -1}{\left(1-f\right)}^{\beta -1}}{\int f^{\alpha -1}{\left(1-f\right)}^{\beta -1}df}\text{\hspace{1em}(8.22)}$$

在哪里

$$\alpha =\bar{f}\left[\frac{\bar{f}\left(1-\bar{f}\right)}{{\bar{f}}^{{}^{\prime }2}}-1\right]\text{\hspace{1em}(8.23)}$$

以及

$$\beta =\left(1-\bar{f}\right)\left[\frac{\bar{f}\left(1-\bar{f}\right)}{\overline{f^{{}^{\prime }2}}}-1\right]\text{\hspace{1em}(8.24)}$$

重要的是，PDF形状 ( p(f) ) 仅是其前两个矩的函数，即平均混合分数 (\bar{f}) 和混合分数方差 (\overline{{f}^{\prime 2}})。因此，在给定Ansys Fluent对流场中每一点的 (\bar{f}) 和 (\overline{{f}^{\prime 2}}) 的预测（公式8.4（第298页）和公式8.5（第298页））后，可以计算假设的PDF形状并将其用作权重函数，以通过公式8.17（第302页）和公式8.19（第302页）（或者对于具有次级流的系统，使用公式8.18（第302页）和公式8.20（第302页））确定组分质量分数、密度和温度的平均值。

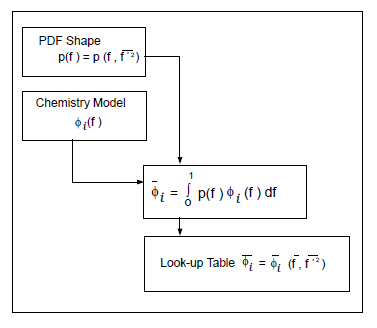
这种逻辑依赖关系在图8.5中以视觉方式展示：平均标量对平均混合分数、混合分数方差和化学模型的逻辑依赖（绝热、单混合分数系统）（第305页），适用于单混合分数。

图8.5：平均标量对平均混合分数、混合分数方差和化学模型的逻辑依赖（绝热、单混合分数系统）

8.1.2.3 非绝热扩展的非预混模型

许多反应系统涉及通过壁面边界、液滴和/或颗粒进行的热传递。在这样的流动中，局部热化学状态不再仅与 ( f ) 相关，还与焓 ( H ) 相关。系统焓影响化学平衡计算以及反应流的温度和组分。因此，在从混合分数计算标量时，必须考虑由于热损失引起的焓变化，如公式8.14（第300页）所示。

在这样的非绝热系统中，湍流波动应通过联合概率密度函数 $p\left(f,H\right)$ 来考虑。然而，对于大多数工程应用而言，计算 $p\left(f,H\right)$ 并不实际。通过假设焓波动与焓水平无关（即热损失对湍流焓波动影响不大），这个问题可以显著简化。在此假设下，$p\left(f,H\right)=p\left(f\right)\delta \left(H-\bar{H}\right)$，并且平均标量计算如下：

$$\overline{{\varphi }_i}={\int }_0^1{\varphi }_i\left(f,\bar{H}\right)p\left(f\right)df\text{\hspace{1em}(8.25)}$$

在非绝热系统中，确定 $\overline{{\varphi }_i}$ 需要求解平均焓的模型传输方程：

$$\frac{\partial }{\partial t}\left(\rho \bar{H}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\bar{H}\right)=\nabla \cdot \left(\frac{k_t}{c_p}\nabla \bar{H}\right)+S_h\text{\hspace{1em}(8.26)}$$

其中，$S_h$ 考虑了由于辐射、向壁面边界的热传递以及与分散相的热交换所引起的源项。

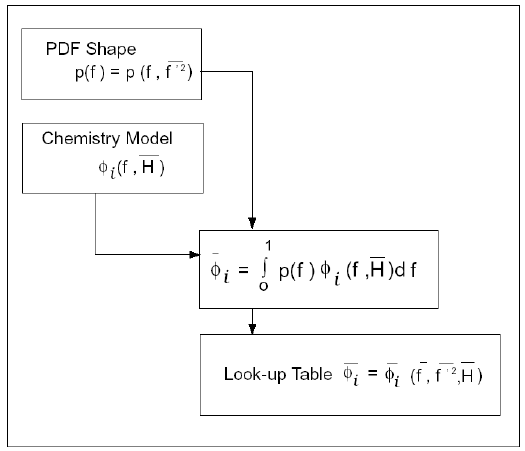
图 8.6：平均标量对平均混合分数、混合分数方差、平均焓以及化学模型的逻辑依赖关系（非绝热、单混合分数系统）（第306页）描述了平均标量值（组分质量分数、密度和温度）对Ansys Fluent在非绝热单混合分数系统中对$\overline{f}$、$\overline{f^{{}^{\prime }2}}$和$\overline{H}$预测的逻辑依赖关系。

图 8.6：平均标量对平均混合分数、混合分数方差、平均焓以及化学模型的逻辑依赖关系（非绝热、单混合分数系统）

当包含次级流时，平均值的计算基于...

$$\overline{{\varphi }_i}={\int }_0^1{\int }_0^1{\varphi }_i\left(f_{\text{fuel }},p_{\text{sec }},\bar{H}\right)p_1\left(f_{\text{fuel }}\right)p_2\left(p_{\text{sec }}\right)d{f}_{\text{fuel }}d{p}_{\text{sec }}\text{\hspace{1em}(8.27)}$$

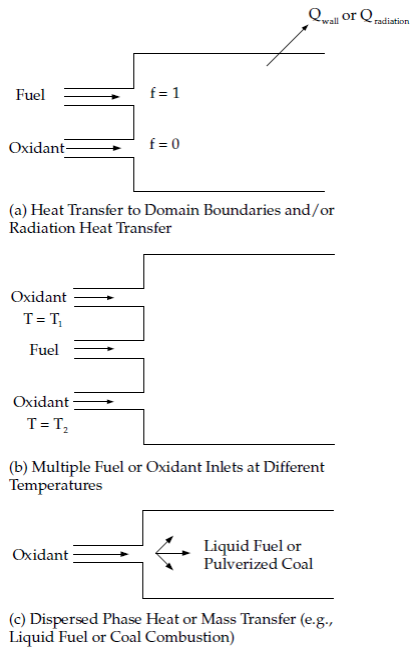
如上所述，在涉及向壁面传热的系统以及包含辐射的系统中，需要对PDF模型进行非绝热扩展。此外，在包含多个燃料或氧化剂入口且入口温度不同的系统中，也需要非绝热模型。最后，在含颗粒流动（例如液体燃料系统或煤燃烧系统）中，当这些流动包括向分散相的传热时，也需要非绝热模型。图8.7：需要非绝热非预混模型方法的反应系统（第307页）展示了几种必须包含PDF模型非绝热形式的系统。

图8.7：需要非绝热非预混模型方法的反应系统

8.1.2.4 化学反应表

8.1.2.4.1 绝热系统的查找表

对于一个平衡、绝热、单一混合分数的情况，平均温度、密度和组分分数仅是 $\bar{f}$ 和 $\overline{f^{{}^{\prime }2}}$ 的函数（见公式8.17（第302页）和公式8.22（第304页））。通过计算这些积分一次，将它们存储在查找表中，并在Ansys Fluent模拟期间检索它们，可以节省大量的计算时间。

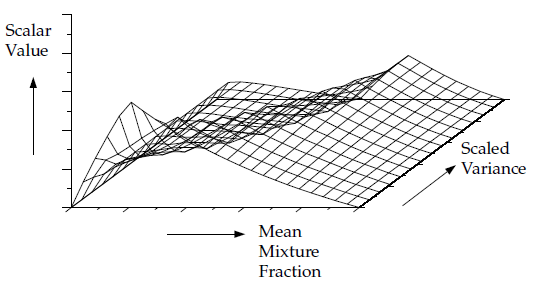
图8.8：绝热单混合分数系统中，标量（质量分数的平均值、密度或温度）作为平均混合分数和混合分数方差的函数的查找表可视化表示（第308页）展示了为单混合分数系统生成的查找表的概念。在给定Ansys Fluent在流场某点预测的$\bar{f}$和$\overline{f^{\prime 2}}$值的情况下，该点的质量分数、密度或温度的平均值$\left({\varphi }_i\right)$可以通过表插值获得。

图8.8：绝热单混合分数系统中，标量（质量分数的平均值、密度或温度）作为平均混合分数和混合分数方差的函数的查找表可视化表示（第308页）是方程8.17（第302页）积分结果的数学表示。每个感兴趣的标量（组分质量分数、密度和温度）都有一个这样的查找表。在绝热系统中，瞬时焓仅是瞬时混合分数的函数，因此，如图8.8：绝热单混合分数系统中，标量（质量分数的平均值、密度或温度）作为平均混合分数和混合分数方差的函数的查找表可视化表示（第308页）所示，只需要一个二维查找表。

图8.8：绝热单混合分数系统中，标量（质量分数的平均值、密度或温度）作为平均混合分数和混合分数方差的函数的查找表可视化表示

对于具有两个混合分数的系统，创建和插值四维查找表的计算成本较高。默认情况下，瞬时性质 ${\varphi }_i$ 以燃料混合分数 $f_{\text{fuel }}$ 和次级部分分数 $p_{\text{sec }}$ 为函数进行表格化（参见方程 8.13，第 300 页），而 PDF 积分（参见方程 8.15，第 300 页）则在运行时执行。图 8.9 展示了这种二维表的视觉表示：绝热双混合分数系统中标量 $\varphi \_1$ 随燃料混合分数和次级部分分数变化的查找表（第 309 页）。或者，也可以在模拟前创建 4D 查找表，并在运行时进行插值（参见用户指南中的“双混合分数模型的完整表格化”）。

图 8.9：绝热双混合分数系统中标量 $\varphi \_$ I 随燃料混合分数和次级部分分数变化的查找表视觉表示

8.1.2.4.2 非绝热系统的 3D 查找表

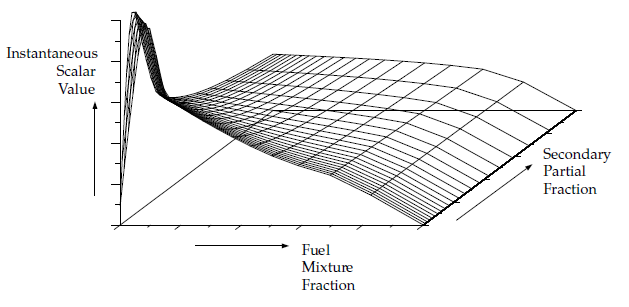
在非绝热系统中，焓值与混合分数之间并非线性关系，而是还依赖于壁面热传递和/或辐射。因此，对于系统中每一个可能的焓值，都需要一张查找表。对于单一混合分数系统，结果就是如图8.10所示的三维查找表：非绝热单一混合分数系统中，标量作为平均混合分数、混合分数方差及归一化热损失/增益函数的查找表可视化表示（第310页）。它由多层二维表格组成，每层对应一个归一化的热损失或增益。第一层对应系统最大热损失，最后一层对应系统最大热增益，而零热损失/增益层则对应绝热表。在绝热层与最大层之间插值得到的层对应热增益，而在绝热层与最小层之间插值得到的层对应热损失。

这个三维查找表使得Ansys Fluent能够根据计算出的$\bar{f},\overline{f^{{}^{\prime }2},}$和$\bar{H}$值，确定每种质量分数、密度和温度。图8.10中的三维表格（非绝热单一混合分数系统中，标量作为平均混合分数、混合分数方差及归一化热损失/增益函数的查找表可视化表示，第310页），实际上是方程8.25（第305页）中积分的可视化呈现。

图8.10：非绝热单一混合分数系统中，标量作为平均混合分数、混合分数方差及归一化热损失/增益函数的查找表可视化表示。

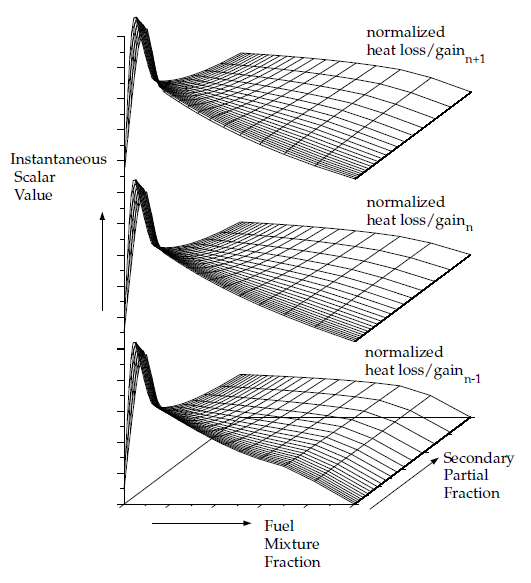
对于非绝热、双混合分数问题，制表和检索方程8.27（第306页）的成本非常高，因为需要五维表格。默认情况下，会创建由方程8.15（第300页）给出的瞬时状态关系的3D查找表。图8.11：非绝热双混合分数系统中作为燃料混合分数、次级部分分数和归一化热损失/增益函数的标量$\varphi \_1$的查找表的视觉表示（第311页）是方程8.15（第300页）的视觉表示。在Ansys Fluent解决方案期间，平均密度是通过在燃料和次级混合分数空间上对瞬时密度进行积分来计算的（参见方程8.27（第306页））。或者，可以在模拟前创建5D查找表，并在运行时进行插值（参见用户指南中的双混合分数模型的完整制表）。一次性预生成5D查找表的成本非常高，但是一旦构建完成，在Ansys Fluent解决方案期间对表进行插值通常比在运行时执行积分要快得多。这对于需要多次迭代或时间步才能收敛的大量单元格的情况尤其如此。

重要提示：请注意，在Ansys Fluent中，双混合分数案例的计算时间将远大于单混合分数问题。在选择双混合分数模型之前，应仔细考虑这一成本。此外，通常从已收敛的单混合分数解决方案开始进行双混合分数模拟是较为便捷的做法。

图8.11：标量 $\varphi$ _I 的查找表视觉表示，作为燃料混合分数和次级部分分数的函数，以及非绝热双混合分数系统中的归一化热损失/增益

8.1.2.4.3 通过自动网格细化生成查找表

Ansys Fluent 具备使用自动网格细化生成查找表的能力。自适应算法在所有表格维度中插入网格点，以确保表格变量（如平均温度、密度和组分质量分数）在连续网格点之间的变化以及它们斜率的变化小于用户指定的容差。自动网格细化的优势在于，表格量仅在变化迅速的区域得到解析。因此，与固定网格相比，将生成更准确和/或更小的 PDF 表格。

在使用自动网格细化时，表格点在用户指定的初始网格点数（默认值为15）的粗网格上计算。如果在点 $i$ 和其邻居 $i+1$ 之间，

$$\left|v_i-v_{i+1}\right|>{\epsilon }_v\left(v_{\max }-v_{\min }\right)\text{\hspace{1em}(8.28)}$$

其中，$v_i$ 表示网格点 $i$ 处的表格变量值，${\epsilon }_v$ 是用户指定的最大值变化率（默认值为0.25），而 $v_{\max }\left(v_{\min }\right)$ 则分别表示所有网格点上的最大（最小）表格值。

除了确保相邻表格点之间的值逐渐变化外，如果满足以下条件，还会添加一个网格点：

$$\left|s_i-s_{i+1}\right|>{\epsilon }_s\left(s_{\max }-s_{\min }\right)\text{\hspace{1em}(8.29)}$$

在任意点 $s_i$ 处，斜率定义为，

$$s_i=\frac{v_{i+1}-v_i}{{\phi }_{i+1}-{\phi }_i}\text{\hspace{1em}(8.30)}$$

在公式8.29（第312页）和公式8.30（第312页）中，${\epsilon }_s$ 是用户指定的最大斜率变化比（默认值为0.25），$s_{\max }\left(s_{\min }\right)$ 是所有网格点上的最大（最小）斜率，而 ${\phi }_i$ 是正在细化的独立网格变量的值（即平均混合分数、混合分数方差或平均焓）。

自动网格细化算法概述如下：首先在平均混合分数维度上创建一个具有指定初始网格点数的初始网格。然后，当两个网格点之间的表格平均温度变化、平均 $\mathrm{H}2$、$\mathrm{CO}$ 和 $\mathrm{OH}$ 摩尔分数变化，或三个网格点之间的斜率变化超过您在最大值/斜率变化比中指定的值时，将插入网格点。此过程重复进行，直到所有点满足指定的值和斜率变化要求，或超过最大网格点数。然后，此过程在混合分数方差维度上重复进行，该维度在平均化学计量混合分数处计算。最后，如果启用了非绝热选项，则在平均焓网格上重复此过程，该网格在平均化学计量混合分数和零混合分数方差处评估。

当使用稳态扩散小火焰面时，自动网格细化可以生成与扩散小火焰面中指定不同的平均混合分数网格点。对于这种情况，使用四阶多项式插值在插入的点上获得小火焰面解。

注意：

二阶插值选项比四阶插值更快，特别是对于高维度的表格，例如非绝热小火焰面。然而，使用二阶插值的欠解析表格可能导致收敛困难。因此，自动网格细化（AGR）选项在生成PDF表格时会最优地放置网格点。因此，通常应使用AGR，特别是对于二阶插值。

注意：

自动网格细化不适用于两个混合分数的情况。

有关用于生成查找表的输入参数的更多信息，请参阅用户指南中的“计算查找表”部分。

8.1.3 使用非预混模型的限制和特殊情况

有关使用非预混模型的限制和特殊情况的信息，请参阅以下部分：

8.1.3.1. 混合分数方法的限制

8.1.3.2. 使用非预混模型进行液体燃料或煤燃烧

8.1.3.3. 使用非预混模型与烟气再循环

8.1.3.4. 使用非预混模型与惰性模型

8.1.3.1 混合分数方法的限制

${\varphi }_i$（组分质量分数、密度或温度）对$f$（方程8.12（第300页）或方程8.14（第300页））的唯一依赖性要求反应系统满足以下条件：

• 化学系统必须是扩散类型，具有离散的燃料和氧化剂入口（喷雾燃烧和粉煤小火焰也可能属于此类）。

• 刘易斯数必须为单位值。（这意味着所有组分和焓的扩散系数相等，这在湍流流动中是一个很好的近似）。

• 当使用单一混合分数时，必须满足以下条件：

• 仅涉及一种类型的燃料。燃料可以是由反应组分的燃烧混合物组成（例如，90%的甲烷和10%的一氧化碳），并且可以包括多个燃料入口。多个燃料入口必须具有相同的组成；不允许有两个或更多燃料入口具有不同的燃料组成（例如，一个入口为甲烷，另一个入口为一氧化碳）。同样，在喷雾燃烧系统或涉及反应颗粒的系统中，只允许一种废气。

• 仅涉及一种类型的氧化剂。氧化剂可以由多种组分的混合物组成（例如，21%的氧气和79%的氮气），并且可以有多个氧化剂入口。然而，多个氧化剂入口必须具有相同的组成。不允许有两个或更多氧化剂入口具有不同的组成（例如，一个入口为空气，另一个入口为纯氧）。

• 当使用两种混合分数时，系统可以涉及三种流。有效的系统如下：

• 两种具有不同组成的燃料流和一种氧化剂流。每种燃料流可以由反应组分的混合物组成（例如，90%的甲烷和10%的一氧化碳）。可以包括每种燃料流的多个入口，但每个燃料入口必须具有两种定义组成中的一种（例如，一个入口为甲烷，另一个入口为一氧化碳）。

• 混合燃料系统，包括气-液、气-煤或液-煤燃料混合物与单一氧化剂。在气-煤或液-煤燃料混合系统中，煤的挥发分和焦炭可视为单一复合燃料流，而次级流可代表另一种燃料。或者，对于煤燃烧，挥发分和焦炭的气体被分别跟踪为不同的燃料流。

• 两种不同组成的氧化剂流和一个燃料流。每个氧化剂流可能由多种组分混合而成（例如，$21\%{\mathrm{O}}_2$ 和 $79\%{\mathrm{N}}_2$）。每个氧化剂流可以有多个入口，但每个入口必须具有两种定义组成中的一种（例如，一个空气入口和一个纯氧入口）。

• 一个燃料流、一个氧化剂流和一个不参与反应的次级流。

• 流动必须是湍流的。

需要强调的是，这些限制排除了直接使用非预混方法模拟预混燃烧的可能性。这是因为未燃烧的预混流远未达到化学平衡。然而，需要注意的是，扩展混合分数公式，即部分预混模型（参见部分预混燃烧（第343页）），可以应用于非预混（带有混合但未燃烧区域）以及部分预混小火焰。

图8.12：可以使用单个混合分数建模的化学系统（第315页）和图8.13：可以使用两个混合分数建模的化学系统配置（第316页）展示了Ansys Fluent中非预混模型可以处理的典型反应系统配置。图8.14：不能使用非预混模型建模的预混系统（第316页）展示了一个不能使用非预混模型建模的预混配置。

图 8.12：可使用单个混合分数建模的化学系统

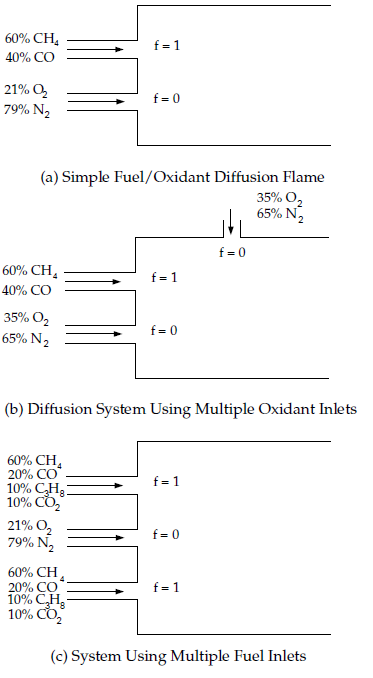
图 8.13：可使用两个混合分数建模的化学系统配置

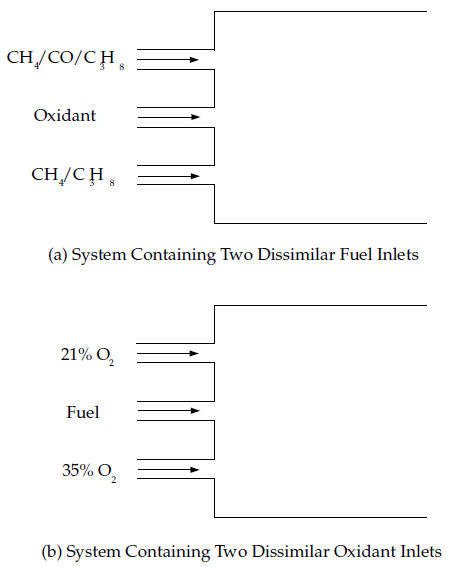
图 8.14：无法使用非预混模型建模的预混系统

8.1.3.2 使用非预混模型进行液体燃料或煤燃烧

如果您的 Ansys Fluent 模拟包括液滴和/或煤颗粒，您可以使用非预混模型。在这种情况下，燃料在计算域内以由分散相的蒸发、挥发分释放和焦炭燃烧定律决定的速率进入气相。对于煤，挥发分和焦炭产物可以定义为两种不同类型的燃料（使用两个混合分数）或作为单一复合排烟（使用一个混合分数），如用户指南中“使用非预混模型模拟煤燃烧”所述。

8.1.3.3 使用非预混模型与烟气再循环

在某些燃烧系统中，烟气再循环（FGR）用于降低小火焰温度并减少 NOx 排放。您可以在 Ansys Fluent 中使用非预混模型来模拟这种情况，方法是将一部分燃烧产物（烟气）从燃烧器的出口再循环回燃烧器入口。这种设置可以通过在 Fluent 中定义一个质量流入口来实现，该入口代表了再循环的烟气。在非预混模型中，再循环的烟气被视为额外的氧化剂源，其成分和温度会影响燃烧过程和最终的排放特性。

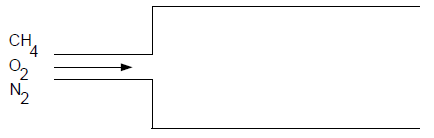
在使用非预混模型解决的大多数问题中，入口通常包含纯氧化剂或纯燃料（即 $f=0$ 或 $f=1$）。然而，如果某个入口的混合分数处于中间值（即 $0<f<1$），只要该入口代表完全反应后的混合物，你也可以将其纳入计算。这种情况在有烟气再循环时会出现，如图8.15所示：《使用非预混模型与烟气再循环》（第317页）。由于 $f$ 是一个守恒量，烟气再循环入口处的混合分数可以计算得出。

$${\dot{m}}_{\text{fuel }}+{\dot{m}}_{\text{recyc }}{f}_{\text{exit }}=\left({\dot{m}}_{\text{fuel }}+{\dot{m}}_{\text{ox }}+{\dot{m}}_{\text{recyc }}\right)f_{\text{exit }}\text{\hspace{1em}(8.31)}$$

或者

$$f_{\text{exit }}=\frac{{\dot{m}}_{\text{fuel }}}{{\dot{m}}_{\text{fuel }}+{\dot{m}}_{\text{ox }}}\text{\hspace{1em}(8.32)}$$

其中，$f_{\text{exit }}$ 表示出口混合分数（即烟气再循环入口处的混合分数），${\dot{m}}_{ox}$ 为氧化剂入口的质量流量，${\dot{m}}_{\text{fuel }}$ 为燃料入口的质量流量，${\dot{m}}_{\text{recyc }}$ 为再循环入口的质量流量。

若包含二次流，

$$f_{\text{fuel, exit }}=\frac{{\dot{m}}_{\text{fuel }}}{{\dot{m}}_{\text{fuel }}+{\dot{m}}_{\text{sec }}+{\dot{m}}_{\text{ox }}}\text{\hspace{1em}(8.33)}$$

以及

$$p_{\text{sec, exit }}=\frac{{\dot{m}}_{\text{sec }}}{{\dot{m}}_{\text{sec }}+{\dot{m}}_{\text{ox }}}\text{\hspace{1em}(8.34)}$$

图8.15：使用非预混模型与烟气再循环

8.1.3.4 结合惰性模型使用非预混模型

为了在不增加两个混合分数的情况下模拟稀释对燃烧的影响，Ansys Fluent允许在计算域中引入惰性流体。与次要混合分数不同，惰性物质不会与主要燃料和氧化剂发生化学平衡——相反，混合后其组成保持恒定。然而，惰性流体确实会影响解，因为它对混合物的焓、比热和密度有影响。惰性物质的守恒方程写为：

$$\frac{\partial \rho Y_I}{\partial t}+\nabla \cdot \left(\overrightarrow{v}\rho Y_I\right)=\nabla \cdot \left(\frac{{\mu }_l+{\mu }_t}{S{c}_t}\nabla \left(Y_I\right)\right)\text{\hspace{1em}(8.35)}$$

其中

$Y_I=$ 惰性流体示踪剂

$S{c}_t=$ 湍流Schmidt数

${\mu }_t=$ 湍流粘度

$\rho =$ 密度

公式8.35（第318页）没有源项或汇项，因为当假设惰性组分具有相同的湍流扩散系数时，问题简化为追踪一个守恒标量。

8.1.3.4.1 混合物组成

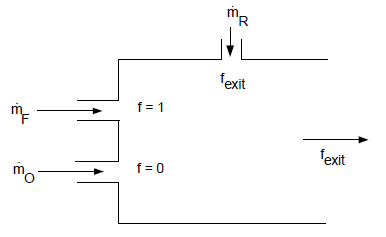
混合物属性根据单元内的混合物分数的平均值 $\left(\overline{f}\right)$ 和方差 $\left(\overline{f}\right)$、反应进度变量 $\left(c\text{, 当部分预混模型启用时}\right)$、单元焓 $(H\text{, 对于非绝热流动})$ 以及惰性示踪剂 $\left(Y_I\right)$ 计算。混合物被建模为惰性和活性组分的混合，但需要使用条件变量访问PDF表。条件化是必要的，以考虑惰性分数所占的体积，同时仍然能够通过简单的查找使用先前构建的表。用于访问PDF表的混合物分数平均值和混合物分数方差由以下公式给出：

$$\overline{f_I}=\frac{\bar{f}}{1-Y_I}\text{\hspace{1em}(8.36)}$$

$$f_I^{\prime 2}=\frac{\overline{f^{\prime 2}}}{{\left(1-Y_I\right)}^2}\text{\hspace{1em}(8.37)}$$

反应进度变量 ( c ) 未受条件限制，然而单元焓值必须经过条件化处理，以考虑惰性焓的影响。惰性焓和活性焓通过以下关系式获得：

$$H\left(T\right)=\left(1-Y_I\right)H^{pdf}\left(T\right)+Y_I{H}^I\left(T\right)\text{\hspace{1em}(8.38)}$$

其中，$H$ 是温度为 $T$ 的单元格的焓值，$H^{pdf}$ 是活性混合分数流的焓值，而 $H^I$ 是惰性流的焓值。这里假设惰性流和活性流的温度相同，但焓值不同。为了计算单元格中的温度，解方程 8.38（第 318 页）以求得温度和 $H^{pdf}$，从而得出能量在惰性流和活性流之间的分配。

惰性焓定义为

$$H^I\left(T\right)=\sum _{i=0}^{N_I}{Y}_i\left(h_i^0+{\int }_{T_0}^T{C}_{p_i}dT\right)\text{\hspace{1em}(8.39)}$$

其中，$Y_i$ 表示惰性流中组分 $i$ 的质量分数，$h_i^0$ 是组分 $i$ 的生成焓，$T_0$ 是参考温度，$C_{D_i}$ 是组分 $i$ 的比热容，而 $N_I$ 是惰性组分的数量。

惰性和PDF焓的定义在用户指南的公式42.11中有进一步说明。

8.1.3.4.1.1 物性计算

混合物的比热容通过以下方式将惰性和活性流混合来评估：

$$C_p\left(T\right)=\left(1-Y_I\right)C_p^{pdf}\left(T\right)+Y_I{C}_p^I\left(T\right)\text{\hspace{1em}(8.40)}$$

混合物的密度是通过对活性流和惰性流的密度进行调和平均计算得出的，这一计算过程根据惰性示踪剂的权重进行了加权处理。

$$\rho \left(T\right)={\left[\frac{\left(1-Y_I\right)}{{\rho }^{pdf}\left(T\right)}+\frac{Y_I}{{\rho }^I\left(T\right)}\right]}^{-1}\text{\hspace{1em}(8.41)}$$

在这里，惰性密度 $\left({\rho }^I\right)$ 是根据理想气体定律计算的。

有关如何设置惰性模型的信息，请参阅用户指南中的“设置惰性模型”部分。

8.1.4 扩散小火焰模型理论

以下各节介绍了小火焰模型信息：

8.1.4.1. 限制与假设

8.1.4.2. 小火焰概念

8.1.4.3. 小火焰生成

8.1.4.4. 小火焰导入

8.1.4.1 限制与假设

以下限制适用于 Ansys Fluent 中的所有扩散小火焰模型：

• 只能模拟单一混合分数；不允许使用双混合分数小火焰模型。

• 假设混合分数遵循 $\beta$ 函数 PDF，并且忽略标量耗散波动。

• 不能将基于经验的流与小火焰模型一起使用。

8.1.4.2 小火焰概念

8.1.4.2.1 概述

小火焰概念将湍流小火焰视为嵌入在湍流流场中的一组薄层流、局部一维小火焰结构集合 [77]（第 1061 页），[512]（第 1087 页），[513]（第 1087 页）（参见图 8.16：层流对流扩散小火焰（第 320 页））。

图 8.16：层流对流扩散小火焰

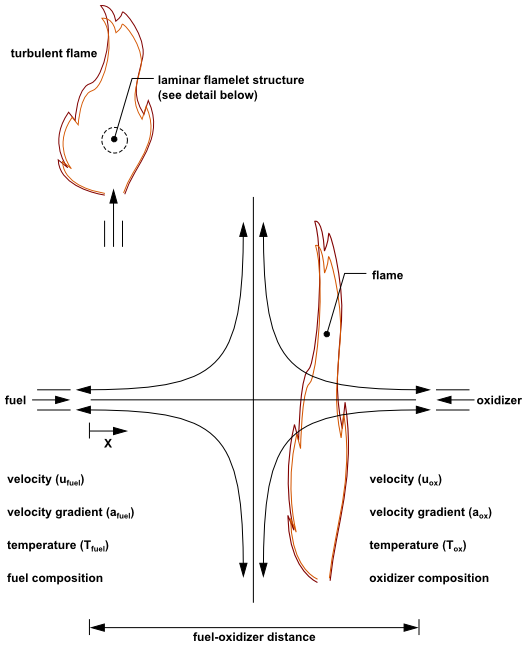
在湍流流动中用于表示小火焰的一种常见层流小火焰类型是对流扩散小火焰。这种几何形状由相对的轴对称燃料和氧化剂射流组成。随着射流间距的减小和/或射流速度的增加，小火焰受到应变并逐渐偏离化学平衡，最终被扑灭。

在层流逆流扩散小火焰实验中，可以测量组分质量分数和温度场，或者更常见的是进行计算。对于后者，存在自相似解，控制方程可以简化为沿着燃料和氧化剂射流轴向的一维形式，在此维度上可以经济地进行复杂的化学计算。

在层流逆流小火焰中，混合分数 $f$（参见混合分数的定义，第296页）从燃料射流处的单位值单调递减至氧化剂射流处的零值。如果将轴向上的组分质量分数和温度从物理空间映射到混合分数空间，它们可以由两个参数唯一描述：混合分数和应变率（或者等效地，标量耗散率 $\chi$，定义在方程8.43，第321页）。因此，化学反应被简化为完全由 $f$ 和 $\chi$ 这两个量描述。

将复杂的化学反应简化为两个变量，使得小火焰面计算可以预处理并存储在查找表中。通过预处理化学反应，计算成本大大降低。

关于逆流层流扩散小火焰的平衡方程、求解方法和示例计算，可以在多个参考文献中找到。Bray和Peters以及Dixon-Lewis的著作中提供了全面的综述和分析（参见文献[77]，第1061页；文献[143]，第1065页）。

8.1.4.2.2 应变率和标量耗散

对于逆流扩散小火焰面，可以定义一个特征应变率 $a_s=v/d$，其中 $v$ 是燃料和氧化剂射流的相对速度，$d$ 是射流喷嘴之间的距离。

为了量化偏离平衡的程度，使用标量耗散 $\chi$ 比使用应变率更为便捷。标量耗散定义为

$$\chi =2D{\left|\nabla f\right|}^2\text{\hspace{1em}(8.42)}$$

其中，$D$ 代表扩散系数。

需要注意的是，标量耗散率 $\chi$ 沿小火焰面轴线方向变化。对于逆流几何结构，小火焰面应变率 $a_s$ 可以通过以下关系与 $f$ 处于化学计量位置处的标量耗散率联系起来 [512]（第 1087 页）：

$${\chi }_{st}=\frac{a_s\exp \left(-2{\left[{\mathrm{erfc}}^{-1}\left(2f_{st}\right)\right]}^2\right)}{\pi }\text{\hspace{1em}(8.43)}$$

其中

${\chi }_{st}=$ 在 $f=f_{st}$ 处的标量耗散率

$a_s=$ 特征应变率

$f_{st}=$ 化学计量混合分数

$erf{c}^{-1}=$ 互补误差函数的逆函数

从物理角度来看，随着小火焰受到应变，反应区的宽度减小，而在化学计量位置 $f=f_{st}$ 处 $f$ 的梯度增加。瞬时化学计量标量耗散率 ${\chi }_{st}$ 被用作基本非平衡参数。它具有 $s^{-1}$ 的量纲，可以解释为特征扩散时间的倒数。在极限 ${\chi }_{st}\to 0$ 下，化学趋于平衡，而随着 ${\chi }_{st}$ 由于气动应变增加，非平衡程度增加。当 ${\chi }_{st}$ 超过临界值时，小火焰会发生局部熄灭。

8.1.4.2.3 在湍流小火焰中嵌入扩散小火焰面

湍流小火焰刷被建模为一系列离散的扩散小火焰面。由于对于绝热系统，扩散小火焰中的组分质量分数和温度完全由 $f$ 和 ${\chi }_{st}$ 参数化，因此湍流小火焰中的密度加权平均组分质量分数和温度可以通过 $f$ 和 ${\chi }_{st}$ 的PDF来确定，如下：

$$\bar{\varphi }=\iint \varphi \left(f,{\chi }_{st}\right)p\left(f,{\chi }_{st}\right)dfd{\chi }_{st}\text{\hspace{1em}(8.44)}$$

其中，$\varphi$ 表示组分质量分数和温度。

在 Ansys Fluent 中，假设 $f$ 和 ${\chi }_{st}$ 在统计上是独立的，因此联合概率密度函数 $p\left(f,{\chi }_{st}\right)$ 可以简化为 $p_f\left(f\right)p_{\chi }\left({\chi }_{st}\right)$。对于 $p_f$，假设其具有 $\beta$ 概率密度函数形状，并在 Ansys Fluent 中求解 $\bar{f}$ 和 $\overline{f^{\prime 2}}$ 的输运方程以确定 $p_f$。忽略 ${\chi }_{st}$ 的波动，因此 $\chi$ 的概率密度函数为 delta 函数：$p_{\chi }=\delta \left(\chi -\overline{{\chi }_{st}}\right)$。在 Ansys Fluent 中，第一个矩，即平均标量耗散率，$\overline{{\chi }_{st}}$，被建模为...

$$\overline{{\chi }_{st}}=\frac{C_{\chi }\overline{f^{{}^{\prime }2}}}{\tau }\text{\hspace{1em}(8.45)}$$

其中，$C_{\chi }$ 是一个常数，默认值为2，而 $\tau$ 是根据湍流模型计算得出的湍流时间尺度。例如，对于RANS湍流模型，

$$\tau =\frac{k}{\epsilon }\text{\hspace{1em}(8.46)}$$

对于非绝热稳态扩散小火焰，需要额外的焓参数。然而，在一定范围内对稳态扩散小火焰进行焓建模的计算成本过高，因此需要进行一些近似处理。假设系统的热量增益/损失对组分质量分数的影响可以忽略不计，并使用绝热质量分数 [62]（第1060页），[464]（第1084页）。然后，对于一系列平均焓增益/损失 $\bar{H}$，通过方程5.8（第173页）计算温度。因此，平均温度和密度PDF表增加了一个平均焓的维度。然而，对于标量耗散为零的情况，不应用恒定的绝热组分质量分数近似。这种情况由非绝热平衡解表示。对于 $\overline{{\chi }_{st}}=0$，组分质量分数被计算为 $\bar{f}$、$\overline{f^{{}^{\prime }2}}$ 和 $\bar{H}$ 的函数。

在Ansys Fluent中，您可以生成自己的扩散小火焰，或者导入由其他独立软件包计算的小火焰文件。这些独立代码包括OPPDIF [401]（第1080页），CFX-RIF [45]（第1059页），[46]（第1059页），[522]（第1087页）和RUN-1DL [516]（第1087页）。Ansys Fluent可以导入标准小火焰文件格式的小火焰文件。

生成和导入扩散小火焰的说明在“小火焰生成”（第323页）和“小火焰导入”（第323页）中提供。

8.1.4.3 小火焰生成

层流逆流扩散小火焰方程可以从物理空间（以$x$为自变量）转换到混合分数空间（以$f$为自变量）[523]（第1087页）。在Ansys Fluent中，解决的是一组简化的混合分数空间方程[522]（第1087页）。在此，针对各组分的质量分数$Y_i$，解算的是$N$个方程。

$$\rho \frac{\partial Y_i}{\partial t}=\frac{1}{2}\rho \chi \frac{{\partial }^2{Y}_i}{\partial f^2}+S_i\text{\hspace{1em}(8.47)}$$

以及一个关于温度的方程式：

$$\rho \frac{\partial T}{\partial t}=\frac{1}{2}\rho \chi \frac{{\partial }^{2}T}{\partial f^2}-\frac{1}{c_p}\sum _i{H}_i{S}_i+\frac{1}{2c_p}\rho \chi \left[\frac{\partial c_p}{\partial f}+\sum _i{c}_{p,i}\frac{\partial Y_i}{\partial f}\right]\frac{\partial T}{\partial f}\text{\hspace{1em}(8.48)}$$

方程8.47（第323页）和方程8.48（第323页）中的符号如下：$Y_i,T,\rho$ 和 $f$ 分别表示第 $i^{\text{th }}$ 种物质的组分质量分数、温度、密度和混合分数。$c_{p,i}$ 和 $c_p$ 分别表示第 $i^{\text{ th }}$ 种物质的比热容和混合物平均比热容。$S_i$ 表示第 $i^{\text{ th }}$ 种物质的反应速率，$H_i$ 表示第 $i^{\text{th }}$ 种物质的具体焓。

标量耗散率 $\chi$ 在小火焰带中必须进行建模。我们采用将方程8.43（第321页）扩展到变密度的方法[303]（第1074页），[523]（第1087页）：

$$\chi \left(f\right)=\frac{a_s}{4\pi }\frac{3{\left(\sqrt{{\rho }_{\infty }/\rho }+1\right)}^2}{2\sqrt{{\rho }_{\infty }/\rho }+1}\exp \left(-2{\left[{\mathrm{erfc}}^{-1}\left(2f\right)\right]}^2\right)\text{\hspace{1em}(8.49)}$$

其中，${\rho }_{\infty }$ 表示氧化剂流体的密度。

根据方程 8.49（第 323 页）给出的应变率定义，混合分数空间中的标量耗散可以表示为：

$$\chi \left(f\right)={\chi }_{st}\frac{\varphi \left(f,\rho \right)}{\varphi \left(f_{st},{\rho }_{st}\right)}\text{\hspace{1em}(8.50)}$$

其中，$f_{st}$ 是化学计量混合分数，${\rho }_{st}$ 是混合密度，而 ${\chi }_{st}$ 是在 $f=f_{st}$ 处的标量耗散率。${\chi }_{st}$ 是用户输入用于生成小火焰面的参数。$\varphi \left(f,\rho \right)$ 和 $\varphi \left(f_{st},{\rho }_{st}\right)$ 使用方程 8.49（第 323 页）进行评估。

8.1.4.4 小火焰面导入

Ansys Fluent 可以导入一个或多个小火焰面文件，将这些扩散小火焰面与假设形状的 PDF（参见方程 8.44（第 322 页））进行卷积，并构建查找表。小火焰面文件可以在 Ansys Fluent 中生成，也可以通过独立的计算机代码生成。

以下类型的小火焰面文件可以导入 Ansys Fluent：

• 由 CFX-RIF 代码 [45]（第 1059 页）、[46]（第 1059 页）、[522]（第 1087 页）生成的 ASCII 文件

• 用户指南中描述的扩散小火焰面建模的标准格式文件，以及 Peters 和 Rogg [516]（第 1087 页）中描述的标准格式文件

当扩散小火焰面在物理空间中生成时，组分和温度在一个空间维度上变化。然后，组分和温度必须从物理空间映射到混合分数空间。如果所有组分的扩散系数相等，则存在混合分数的唯一定义。然而，在存在差异扩散的情况下，混合分数可以有多种定义方式。

Ansys Fluent 通过以下方式之一计算沿扩散小火焰面的混合分数分布：

• 从文件中读取（仅限标准格式文件）

此选项适用于在混合分数空间中求解的扩散小火焰面。若选择此方法，Ansys Fluent将查找混合分数关键字$z$，如Peter和Roggs的工作[516]（第1087页）中所述，并获取相关数据。若Ansys Fluent在小火焰面文件中未找到混合分数数据，则将采用下述烃类公式方法。

• 烃类公式

依据Bilger等人的研究[61]（第1060页），混合分数的计算方式如下：

$$f=\frac{b-b_{ox}}{b_{\text{fuel }}-b_{ox}}\text{\hspace{1em}(8.51)}$$

以下文本的中文翻译：

$$b=2\frac{Y_C}{M_{w,C}}+0.5\frac{Y_H}{M_{w,H}}-\frac{Y_O}{M_{w,O}}\text{\hspace{1em}(8.52)}$$

$Y_C,Y_H$ 和 $Y_O$ 分别表示碳、氢和氧原子的质量分数，而 $M_{w,C},M_{w,H}$ 和 $M_{w,O}$ 则是它们的分子量。$b_{ox}$ 和 $b_{\text{fuel}}$ 分别表示在氧化剂入口和燃料入口处的 $b$ 值。

多重小火焰面数据集中的小火焰面轮廓应在施加的应变率上有所变化；组分和边界条件应保持一致。此外，建议从多重小火焰面数据集中排除熄灭的小火焰面。多重扩散小火焰面的格式如下：

• 标准格式：如果您有一组标准格式的小火焰面文件，可以一次性导入它们，Ansys Fluent 会在内部将它们合并成一个多重小火焰面文件。当您导入这组小火焰面文件时，Ansys Fluent 会搜索并计算 HEADER 关键字的出现次数，以确定文件中扩散小火焰面的数量。

• CFX-RIF 格式：CFX-RIF 小火焰面文件包含在不同应变率下的多个扩散小火焰面，且该文件不应手动修改。只能导入一个 CFX-RIF 小火焰面文件。

对于任一类型的文件，Ansys Fluent 将确定小火焰面轮廓的数量，并按应变率升序排列。对于在物理空间中生成的扩散小火焰面，您可以选择四种可用方法之一来计算混合分数。标量耗散将根据应变率使用公式 8.43（第 321 页）计算。

8.1.5 稳态扩散小火焰面模型理论

稳态小火焰片方法将湍流小火焰刷模拟为一系列离散的、稳态的层流小火焰，这些小火焰被称为扩散小火焰片。各个扩散小火焰片被假定具有与简单配置中的层流小火焰相同的结构，并通过实验或计算获得。使用详细的化学机理，Ansys Fluent能够计算非预混燃烧的层流对流扩散小火焰片。然后，这些扩散小火焰片通过统计PDF方法嵌入到湍流小火焰中。

扩散小火焰片方法的优势在于，可以将真实的化学动力学效应纳入湍流小火焰中。随后，化学反应可以预处理并表格化，从而大幅节省计算资源。然而，稳态扩散小火焰片模型仅限于模拟化学反应相对较快的燃烧过程。该模型假设小火焰对气动应变立即响应，因此无法捕捉如点火、熄灭和慢速化学反应（如NOx）等深度非平衡效应。

以下章节将严格介绍稳态扩散小火焰片模型的相关信息：

8.1.5.1. 概述

8.1.5.2. 多稳态小火焰片库

8.1.5.3. 稳态扩散小火焰片自动网格细化

8.1.5.4. 非绝热稳态扩散小火焰片

有关混合分数模型的常规信息，请参阅引言（第295页）。

8.1.5.1 概述

在扩散小火焰中，分子层面上的燃料和氧化剂会扩散到反应区。在那里，它们遇到高温和自由基并被点燃。反应区中产生更多的热量和自由基，其中一部分会扩散出去。在近平衡小火焰中，反应速率远快于扩散速率。然而，当小火焰被湍流拉伸和变形时，组分和温度梯度增加，自由基和热量更快地从小火焰中扩散出去。组分达到化学平衡的时间更少，局部非平衡程度增加。

稳态扩散小火焰模型适用于预测由于湍流引起的小火焰气动应变导致的化学非平衡。然而，假定化学反应对这种应变响应迅速，因此当应变松弛至零时，化学反应趋向于平衡。

当化学时间尺度与流体混合时间尺度相当时，组分可以被认为处于全局化学非平衡状态。此类情况包括NOx形成和低温$\mathrm{CO}$氧化。稳态扩散小火焰模型不适用于这种慢化学小火焰。相反，您可以使用以下模型之一来模拟慢化学：

• 非稳态扩散小火焰模型（参见非稳态扩散小火焰模型理论（第327页））

• NOx模型中的痕量组分假设（参见污染物形成（第363页））

• 层流有限速率模型（参见反应建模的广义有限速率公式（第243页）），其中忽略了湍流-化学相互作用。

• EDC模型（参见涡耗散概念（EDC）模型（第249页））

• PDF输运模型（参见成分PDF输运（第276页））。

8.1.5.2. 多稳态小火焰库

Ansys Fluent 能够在一定的应变率范围内生成多个稳态扩散小火焰，以适应多维模拟中变化的应变场。如果您指定的扩散小火焰数量大于一个，那么扩散小火焰将在标量耗散值处生成，这些值由方程8.53（第326页）确定。

$${\chi }_i=\{\begin{array}{cc}10{\chi }_{i-1}& \text{for}{\chi }_{i-1}<1s^{-1}\\ {\chi }_{i-1}+\Delta \chi & \text{for}{\chi }_{i-1}\ge 1s^{-1}\end{array}\text{\hspace{1em}(8.53)}$$

在指定的扩散小火焰最大数量范围内，$i$ 从 1 开始取值，${\chi }_0$ 是方程 8.50（第 323 页）中给出的化学计量混合分数 ${\chi }_{st}$ 处的初始标量耗散率，$\Delta \chi$ 是标量耗散步长。扩散小火焰的生成持续进行，直到达到最大小火焰数量或小火焰熄灭。熄灭的小火焰不包含在小火焰库中。

8.1.5.3 稳态扩散小火焰自动网格细化

默认情况下，一维小火焰网格通过在化学计量混合分数附近（近似为峰值温度位置）固定数量的点进行聚类离散化。Ansys Fluent 还提供了稳态扩散小火焰的自动网格细化选项，其中自适应算法插入网格点，使得相邻网格点之间的值变化以及斜率变化小于用户指定的容差。

使用自动网格细化时，在用户指定的小火焰中初始网格点数（默认 8 个）的粗网格上计算稳态解。收敛后，如果点 $i$ 与其邻居 $i+1$ 之间的变化超过一定阈值，则在点 $i$ 和 $i+1$ 之间插入一个新的网格点。

$$\left|v_i-v_{i+1}\right|>{\epsilon }_v\left(v_{\max }-v_{\min }\right)\text{\hspace{1em}(8.54)}$$

其中，$v_i$ 表示在网格点 $i$ 处的温度和组分质量分数的值，${\epsilon }_v$ 是用户指定的最大值变化率（默认值为 0.5），而 $v_{\max }\left(v_{\min }\right)$ 则表示所有网格点中的最大（最小）值。

此外，如果某个网格点满足以下条件，则会添加一个新的网格点：

$$\left|s_i-s_{i+1}\right|>{\epsilon }_s\left(s_{\max }-s_{\min }\right)\text{\hspace{1em}(8.55)}$$

斜率 $s_i$ 的定义如下：

$$s_i=\frac{v_{i+1}-v_i}{f_{i+1}-f_i}\text{\hspace{1em}(8.56)}$$

在公式8.55（第326页）和公式8.56（第326页）中，${\epsilon }_s$ 是用户指定的最大斜率变化比（默认值为0.5），$s_{\max }\left(s_{\min }\right)$ 是所有网格点上的最大（最小）斜率，而 $f_i$ 是网格点 $i$ 的混合分数值。

经过细化的小火焰层会重新收敛，细化过程会重复进行，直到不再有网格点被公式8.54（第326页）和公式8.55（第326页）添加，或者超过了用户指定的小火焰层中最大网格点数（默认值为64）。

8.1.5.4 非绝热稳态扩散小火焰层

对于非绝热稳态扩散小火焰层，Ansys Fluent 遵循 [62]（第1060页）和 [464]（第1084页）的方法，并假设小火焰层组分分布不受小火焰层的热量损失/增加影响。无需生成特殊的非绝热小火焰层分布，避免了非常繁琐的预处理步骤。此外，Ansys Fluent 与外部稳态扩散小火焰层生成包（例如，OPPDIF、CFX-RIF、RUN-1DL）的兼容性得以保留。该模型的缺点是未考虑热量损失对组分质量分数的影响，也未考虑热量损失对熄灭极限的影响。

扩散小火焰层生成后，小火焰层分布会与假设形状的PDF进行卷积，如公式8.44（第322页）所示，然后在Ansys Fluent中进行查找表化。非绝热PDF表具有以下维度：

$$\overline{T}\left(\overline{f},\overline{f^{{}^{\prime }2}},\overline{H},\overline{{\chi }_{st}}\right)$$

对于 $\chi =0$（即，平衡解），有 $\overline{Y_i}\left(\bar{f},\overline{f^{\prime 2}},\bar{H}\right)$。

$$\overline{Y_i}\left(\bar{f},\overline{f^{{}^{\prime }2}},\overline{{\chi }_{st}}\right)\text{for}\chi \ne 0$$

$$\overline{\rho }\left(\overline{f},\overline{f^{{}^{\prime }2}},\overline{H},\overline{{\chi }_{st}}\right)$$

在 Ansys Fluent 的求解过程中，求解了平均混合分数、混合分数方差和平均焓的方程。标量耗散场从湍流场和混合分数方差（公式 8.45，第 322 页）计算得出。单元格温度、密度和组分质量分数的平均值从 PDF 查找表中获得。

8.1.6 非稳态扩散小火焰模型理论

稳态扩散小火焰模型，如《扩散小火焰模型理论》（第 319 页）和《稳态扩散小火焰模型理论》（第 324 页）所述，模拟了由于湍流的应变效应导致的局部化学非平衡。在许多燃烧器中，出口处的应变较小，稳态扩散小火焰模型预测所有组分，包括像 NOx 这样的缓慢形成组分，都接近平衡，这通常是不准确的。这种不准确的原因在于小火焰时间尺度（标量耗散的倒数）与缓慢形成组分的时间尺度（自组分在燃烧器中混合后开始积累的停留时间）之间的差异。

Ansys Fluent 中的非稳态扩散小火焰模型可以比稳态扩散小火焰模型更准确地预测缓慢形成组分，如气体污染物或液体反应器中的产品产率。计算昂贵的化学动力学被简化为一维，并且该模型比在二维或三维中计算动力学的层流有限速率、EDC 或 PDF 传输模型显著更快。非稳态小火焰模型有两种变体，即欧拉非稳态小火焰模型（参见《欧拉非稳态层流小火焰模型》（第 328 页））和用于预测压缩点火发动机燃烧的柴油非稳态小火焰模型（参见《柴油非稳态层流小火焰模型》（第 330 页））。

以下各节详细介绍了与非稳态小火焰面模型相关的信息：

8.1.6.1. 欧拉非稳态层流小火焰面模型

8.1.6.2. 柴油非稳态层流小火焰面模型

8.1.6.3. 多重柴油非稳态小火焰面

8.1.6.4. 带小火焰面重置的多重柴油非稳态小火焰面

8.1.6.1 欧拉非稳态层流小火焰面模型

欧拉非稳态层流小火焰面模型可用于预测非化学平衡状态下缓慢形成的中间产物和最终产物。典型的缓慢形成组分包括气相污染物如NOx，以及液态反应器中的产物化合物。通过将化学计算简化为一维，可以在复杂的3D几何结构中经济地模拟具有多个组分和刚性反应的详细动力学。

该模型基于Barths等人[46]（第1059页）和Coelho与Peters[112]（第1063页）的工作，对稳态收敛流动场上的非稳态标记概率方程进行后处理。标记场表示在任意时间和空间点找到小火焰面的概率。为每个小火焰面求解一个概率标记输运方程。

在Ansys Fluent中，在开始非稳态小火焰面模拟之前，必须使用稳态扩散小火焰面模型（参见稳态扩散小火焰面模型理论（第324页））计算稳态流动解。由于非稳态小火焰面方程是在稳态小火焰面解上进行后处理的，因此忽略了非稳态小火焰面组分对流场的影响。

当启用多个小火焰面时，Ansys Fluent求解表示第$n^{\text{th}}$小火焰面燃料概率的欧拉输运方程$I_n$，如下所示：

$$\frac{\partial \left(\rho I_n\right)}{\partial t}+\nabla \cdot \left(\rho \overrightarrow{v}{I}_n\right)=\nabla \cdot \left(\left(\frac{k}{C_p}+\frac{{\mu }_t}{{\sigma }_t}\right)\nabla I_n\right)\text{\hspace{1em}(8.57)}$$

其中，$k$ 是混合物的层流热导率，$C_p$ 是混合物的比热容，而 ${\sigma }_t$ 是普朗特数。

每个标记的概率初始化为，

$$I_n=\{\begin{array}{ll}1& \text{ for }{\chi }_{\min ,n}<\chi \le {\chi }_{\max ,n}\text{ and }\bar{f}\ge f_{\text{init }}\\ 0& \text{ for }\chi <{\chi }_{\min ,n}\text{ or }\chi >{\chi }_{\max ,n}\text{ or }\bar{f}<f_{\text{init }}\end{array}\text{\hspace{1em}(8.58)}$$

其中，$\chi$ 表示标量耗散率，${\chi }_{\min ,n}$ 和 ${\chi }_{\max ,n}$ 分别是第 $n^{\text{th }}$ 小火焰面标记概率的最小和最大标量耗散值，$\bar{f}$ 是平均混合分数，而 $f_{\text{init }}$ 是一个用户指定的常数，应设置为大于化学计量混合分数的值。因此，标记概率在平均混合分数大于用户指定值（通常大于化学计量值）的区域内初始化为1，多个小火焰面通过标量耗散将这一初始区域细分。

如前所述，欧拉非定常层流小火焰面模型仅适用于稳态模拟。然而，标记概率输运方程（方程8.57，第328页）始终以时间精确方式求解，因为初始标记概率在稳态流场中对流和扩散。在入口边界处，$I_n$ 设为零，因此随着 $I_n$ 被对流和扩散出域外（对于有出口边界的情况），$I_n$ 场随时间减小至零。

非定常小火焰面组分方程（方程8.47，第323页）与每个标记概率 $I_n$ 的标记概率方程（方程8.57，第328页）同时积分。对于液相化学，初始小火焰面场是混合但未燃烧的小火焰面，因为假设液相反应在混合后立即进行。气相化学涉及点火，因此初始小火焰面场从稳态扩散小火焰面解计算得出。所有慢形成组分，如NOx，必须在求解非定常小火焰面方程之前识别。所有慢形成组分的质量分数在此初始小火焰面轮廓中设为零，因为在点火时，几乎没有停留时间用于显著形成。

在化学计量混合分数处的标量耗散率 $\left({\chi }_{st,n}\right)$ 是每个小火焰let组分方程所需的参数。这一参数在每个时间步长中根据稳态Ansys Fluent场的概率加权体积积分[112]（第1063页）进行计算：

$${\chi }_{st,n}\left(t\right)=\frac{{\int }_V{I}_n{\left({\bar{\chi }}_{st}\left(\overrightarrow{x}\right)\right)}^{\frac{3}{2}}\rho \left(\overrightarrow{x}\right)dV}{{\int }_V{I}_n{\left({\bar{\chi }}_{st}\left(\overrightarrow{x}\right)\right)}^{\frac{1}{2}}\rho \left(\overrightarrow{x}\right)dV}\text{\hspace{1em}(8.59)}$$

其中，$\overline{{\chi }_{st}}$ 在公式 8.45（第 322 页）中定义，$V$ 表示流体体积。Ansys Fluent 提供了将 $\overline{{\chi }_{st}}$ 限制为用户指定最大值的选项，该值应大致等于小火焰熄灭时的标量耗散率（可以在单独的模拟中使用稳态扩散小火焰求解器计算此熄灭标量耗散率）。

为了在高标量耗散率下避免小火焰熄灭，并考虑非绝热热损失或增益，未求解非稳态小火焰能量方程。对于绝热情况，在每个时间步长从稳态扩散小火焰库中根据公式 8.59（第 329 页）的概率加权标量耗散率 ${\chi }_{st}$ 计算小火焰温度 $T^{ad}\left(f,t\right)$。对于非绝热情况，则在时间 $t$ 时从...

$$T\left(f,t\right)=T^{ad}\left(f,t\right)\xi \left(f,t\right)\text{\hspace{1em}(8.60)}$$

以下是您提供的文本的中文翻译：

"在哪里"

$$\xi \left(f,t\right)=\frac{{\int }_{V}I\rho \bar{T}\left(\overrightarrow{x}\mid f\right)/T^{ad}\left(f,t\right)dV}{{\int }_{V}I\rho dV}\text{\hspace{1em}(8.61)}$$

(8.61)

为简洁起见，此处省略了下标 $n$，该下标指代第 $n$ 个小火焰面。$\overline{T}\left(\overrightarrow{x}\mid f\right)$ 表示基于局部单元混合分数的 Ansys Fluent 稳态平均单元温度。

每个单元内的非稳态小火焰面平均组分质量分数随时间累积，可表示为：

$${\tilde{Y}}_k=\frac{\sum _n{\int }_t{I}_n\left(t\right)⟨Y_{k,n}⟩dt}{\sum _n{\int }_t{I}_n\left(t\right)dt}\text{\hspace{1em}(8.62)}$$

其中，${\tilde{Y}}_k$ 表示第 $k^{\text{th }}$ 种组分的非稳态小火焰面质量分数，而 $Y_{k,n}$ 则是第 $n^{\text{th }}$ 个小火焰面的第 $k^{\text{th }}$ 种非稳态小火焰面质量分数，其计算采用 Beta 分布概率密度函数（pdf）进行，如下所示：

$$⟨Y_{k,n}⟩={\int }_0^1{Y}_{k,n}\left(f\right)P\left(f\right)df\text{\hspace{1em}(8.63)}$$

概率标记方程（方程8.57（第328页））和小火焰面组分方程（方程8.47（第323页））一起随时间推进，直到概率标记显著对流和扩散出计算域。从方程8.61（第329页）计算得到的非定常小火焰面平均组分，随着概率标记$I_n$消失，达到稳态。

8.1.6.1.1 液体反应

液体反应器通常具有以下特点：

• 密度和温度接近恒定。

• 反应相对缓慢，组分远离化学平衡。

• 高施密特数$\left(Sc\right)$，因此分子扩散减少。

欧拉非定常层流小火焰面模型可用于模拟液体反应。当启用液体微混合模型时，Ansys Fluent使用体积加权混合律公式计算密度。

高$Sc$的影响是减少最小尺度（微观）上的混合，并增加混合分数方差，这通过湍流混合器模型[38]（第1059页）进行建模。为湍流标量谱的惯性对流$\left(\overline{f_{ic}^{{}^{\prime }2}}\right)$、粘性对流$\left(\overline{f_{vc}^{{}^{\prime }2}}\right)$和粘性扩散$\left(\overline{f_{vd}^{\prime 2}}\right)$子范围分别求解三个输运方程。

$$\frac{\partial }{\partial t}\left(\rho \overline{f_{ic}^{{}^{\prime }2}}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overline{f_{ic}^{{}^{\prime }2}}\right)=\nabla \cdot \left(\left(\frac{k}{C_p}+\frac{{\mu }_t}{{\sigma }_t}\right)\nabla \overline{f_{ic}^{{}^{\prime }2}}\right)+C_1{\mu }_t\cdot {\left(\nabla \bar{f}\right)}^2-C_2\rho \frac{\epsilon }{k}\overline{f_{ic}^{{}^{\prime }2}}\text{\hspace{1em}(8.64)}$$

$$\frac{\partial }{\partial t}\left(\rho \overline{f_{vc}^{{}^{\prime }2}}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overline{f_{vc}^{{}^{\prime }2}}\right)=\nabla \cdot \left(\left(\frac{k}{C_p}+\frac{{\mu }_t}{{\sigma }_t}\right)\nabla \overline{f_{vc}^{{}^{\prime }2}}\right)+C_2\rho \frac{\epsilon }{k}\overline{f_{ic}^{{}^{\prime }2}}-C_3\rho \sqrt{\frac{\epsilon }{\nu }}\cdot \overline{f_{vc}^{{}^{\prime }2}}\text{\hspace{1em}(8.65)}$$

$$\frac{\partial }{\partial t}\left(\rho \overline{f_{vd}^{{}^{\prime }2}}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overline{f_{vd}^{{}^{\prime }2}}\right)=\nabla \cdot \left(\left(\frac{k}{C_p}+\frac{{\mu }_t}{{\sigma }_t}\right)\nabla \overline{f_{vd}^{{}^{\prime }2}}\right)+C_3\rho \sqrt{\frac{\epsilon }{\nu }}\cdot \left(\overline{f_{vc}^{{}^{\prime }2}}-\left(C_4+\frac{C_5}{Sc}\right)\overline{f_{vd}^{{}^{\prime }2}}\right)\text{\hspace{1em}(8.66)}$$

其中，$k$ 是混合物的层流热导率，$C_p$ 是混合物的比热容，${\sigma }_t$ 是普朗特数。常数 $C_1$ 到 $C_5$ 的值分别为 2、1.86、0.058、0.303 和 17050。总混合物分数方差是 $\overline{f_{ic}^{{}^{\prime }2}}$、$\overline{f_{vc}^{{}^{\prime }2}}$ 和 $\overline{f_{vd}^{{}^{\prime }2}}$ 的总和。

在方程 8.66（第 330 页）中，单元施密特数 $Sc$ 计算为 $Sc=\mu /\rho D$，其中 $\mu$ 是粘度，$\rho$ 是密度，$D$ 是质量扩散率，如 $pdf$ 混合物材料所定义。

8.1.6.2 柴油机非稳态层流小火焰模型

在柴油发动机中，喷入气缸的燃料蒸发，与周围气体混合，然后在压缩作用下温度和压力升高时自燃。基于 Pitsch 等人以及 Barths 等人 [522]（第 1087 页），[45]（第 1059 页）的工作，柴油机非稳态层流小火焰模型通过有限数量的一维层流小火焰来模拟化学反应。通过将昂贵的化学动力学计算简化为 1D，与层流有限速率、EDC 或 PDF 传输模型相比，可以显著节省运行时间。

小火焰组分和能量方程（方程 8.47（第 323 页）和方程 8.48（第 323 页））与流动同时求解。使用来自流动的属性对小火焰方程进行分数步长推进，然后使用来自小火焰的属性对流动进行相同的分数时间步长推进。

每个小火焰子在引入计算域时的初始条件是一种混合但未燃烧的分布。对于小火焰子分数时间步长，流场求解器会将体积平均的标量耗散率和压力，以及燃料和氧化剂的温度传递给小火焰子求解器。为了考虑压缩过程中的温度升高，小火焰子能量方程（方程8.48，第323页）在右侧增加了一个额外的项。

$$\dot{q}=\frac{1}{c_p}\frac{\partial p}{\partial t}\text{\hspace{1em}(8.67)}$$

其中，$c_p$ 表示比热容，$p$ 为气缸内体积平均压力。这种因压缩导致的小火焰温度上升最终会引起小火焰的点燃。

在小火焰方程经过部分时间步长推进后，创建一个非绝热稳态小火焰表（参见非绝热稳态扩散小火焰（第327页））。利用该表中的属性，随后对CFD流场进行相同的部分时间步长推进。

8.1.6.3 多重柴油非稳态小火焰

在某些应用中，燃烧域内不同区域的点火时间不同，单一小火焰无法准确表示化学反应。例如，分裂喷射和高停留时间喷雾。在这些情况下，早期喷射的蒸发喷雾由于停留时间较长，会比后期喷射的喷雾更早点燃。单一小火焰无法模拟后期喷雾的局部点火延迟，因为单一小火焰代表已燃烧状态。通过使用多个小火焰可以克服这一缺陷，这些小火焰在模拟过程中用户指定的时间在反应域内生成。新小火焰继承了在新小火焰引入时计算的前一小火焰边界温度，小火焰组分场初始化为混合但未燃烧状态。

求解 $N-1$ 个小火焰的标记概率方程（方程8.57（第328页）），其中 $N$ 为非稳态小火焰的总数。最后一个小火焰的标记概率按以下方式获得：

$$I_N=\bar{f}-\sum _{n=1}^{N-1}{I}_n\text{\hspace{1em}(8.68)}$$

其中，$\bar{f}$ 表示平均混合分数，而 $I_n$ 则是第 $n^{\text{ th }}$ 个非稳态小火焰的标记概率。第 $n^{\text{th }}$ 个小火焰的标量耗散率通过方程 8.59（第 329 页）计算得出。

PDF 表中的属性 $\phi \left(t\right)$（如质量分数、比热等）是根据每个小火焰的加权贡献计算的：

$$⟨\phi \left(t\right)⟩=\frac{\sum _{n=1}^{N-1}{I}_n\left(t\right)⟨{\phi }_n\left(t\right)⟩}{\sum _{n=1}^{N-1}{I}_n\left(t\right)}\text{\hspace{1em}(8.69)}$$

其中，${\phi }_n$ 表示第 n 个小火焰片的属性。

柴油非稳态小火焰片方法能够模拟点火以及产物、中间体和污染物的形成。关于柴油非稳态小火焰片模型的设置，请参阅《Fluent 用户指南》中的“使用柴油非稳态层流小火焰片模型”部分。

8.1.6.4 具有小火焰片重置的多个柴油非稳态小火焰片

随着多个柴油非稳态小火焰片点火，它们的组分和温度场趋向于相同的化学平衡状态，随着标量耗散（混合）的减少。为了模拟多个发动机循环，Ansys Fluent 允许小火焰片重置事件，这将多个小火焰片重置为一个小火焰片。此外，在循环结束时，通常会有一些燃烧气体被捕获并在下一循环中与新鲜进气混合。可以通过使用柴油非稳态小火焰片重置或惰性模型（通过惰性 EGR 重置）来模拟发动机室中废气的存在。

有关如何使用和设置柴油非稳态小火焰片重置和惰性 EGR 重置选项的信息，请参阅《Fluent 用户指南》中的“重置柴油非稳态小火焰片”部分。

8.1.6.4.1 重置小火焰片

在燃烧冲程结束且进气阀打开之前，除第一个小火焰片外的所有现有小火焰片都被删除，第一个小火焰片的概率设置为：

$$I_1=\sum _{n=1}^{n=N}{I}_n$$

其中，$I_n$ 表示第 $n^{\text{th}}$ 个小火焰条的概率，$N$ 是小火焰条的总数。重置小火焰条的混合物组成（以及类似的温度）设定如下：

$${⟨Y_k⟩}_1=\sum _{n=1}^N{I}_n\left(t\right){⟨Y_k⟩}_n$$

其中，${⟨Y_k⟩}_n$ 表示从第 $n^{\text{th}}$ 个小火焰片中得到的第 $k^{\text{th}}$ 种物质的组分质量分数。

在重置小火焰片后，计算将基于这个单一的、通常为已燃状态的小火焰片进行。后续小火焰片的起始时间应设定在燃料喷射之前。因此，喷射的燃料在第二个及更高编号的小火焰片中进行建模。整个过程通过动态网格事件进行控制，具体描述见 Fluent 用户指南中的“柴油非定常小火焰片重置”部分。