以下各节介绍了有壁面约束的湍流流动的近壁面处理相关信息：

• 4.18.1 概述
• 4.18.2 基于$\epsilon$模型的壁面处理
• 4.18.3 基于$\omega$湍流模型的y+不敏感近壁面处理
• 4.18.4 LES近壁面处理
• 4.18.5 湍流壁面约束流动中的壁面粗糙度效应

4.18.1 概述

湍流流动受壁面存在的影响显著。显然，平均速度场通过壁面必须满足的无滑移条件受到影响。然而，湍流也会以非平凡的方式因壁面的存在而改变。非常接近壁面时，粘性阻尼减少了切向速度波动，而运动学阻塞减少了法向波动。然而，在近壁区域的外部，由于平均速度的巨大梯度，湍流迅速增强，产生了湍流动能。

近壁面建模对数值解的准确性有重要影响，因为壁面是平均涡量和湍流的主要来源。毕竟，正是在近壁面区域，解变量具有大梯度，动量和其他标量传输最为剧烈。因此，近壁面区域流动的准确表示决定了有壁面约束湍流流动预测的成功与否。

众多实验表明，近壁区域大致可分为三个层次。在最内层，即所谓的“粘性子层”，流动几乎是层流的，分子粘性在动量和热量或质量传递中起主导作用。在外层，称为完全湍流层，湍流起主要作用。最后，在粘性子层和完全湍流层之间存在一个过渡区域，分子粘性和湍流的影响同等重要。图4.15：近壁区域的细分（第136页）以半对数坐标绘制了这些近壁区域的细分。

图4.15：近壁区域的细分

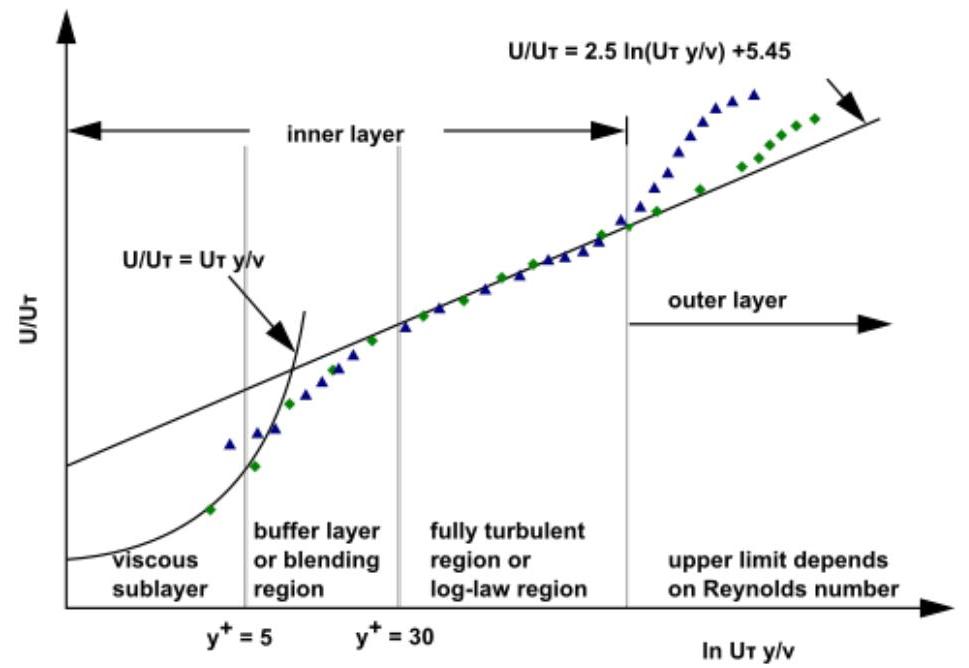
在图4.15：近壁区域的细分（第136页）中，$y^{+}\equiv \rho u_{\tau }y/\mu$，其中$u_{\tau }$是摩擦速度，定义为$\sqrt{\frac{{\tau }_w}{\rho }}$。

4.18.1.1 壁面函数与近壁模型

传统上，近壁区域有两种建模方法。一种方法是不解析受粘性影响的内层区域（粘性子层和缓冲层），而是使用称为“壁面函数”的半经验公式来桥接壁面和完全湍流区域之间的受粘性影响的区域。使用壁面函数无需修改湍流模型以考虑壁面的存在。

另一种方法则是修改湍流模型，以便能够在网格一直延伸到壁面（包括粘性子层）的情况下解析受粘性影响的区域。为了便于讨论，这将被称作“近壁建模”方法。这两种方法在图4.16：Ansys Fluent中的近壁处理（第137页）中以示意图形式展示。

图4.16：Ansys Fluent中的近壁处理

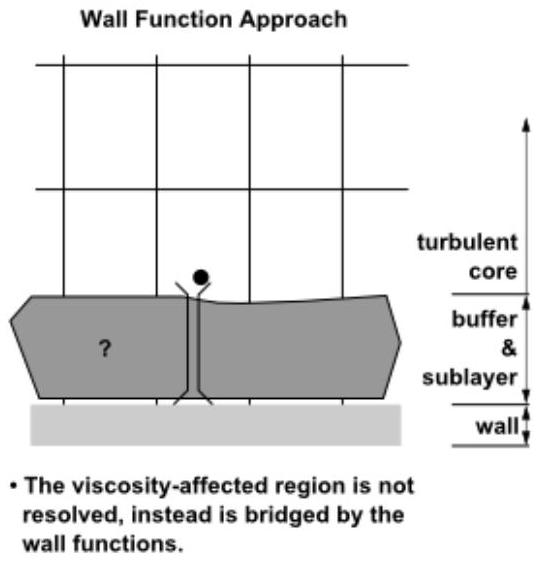
• 湍流模型应当有效

• 高雷诺数湍流模型可以在整个近壁区域使用。

所有壁面函数（可扩展壁面函数除外）的主要缺点是，在壁面法向方向上对网格进行细化时，数值结果会逐渐恶化。当$y^{+}$值小于15时，壁面剪应力和壁面热传递的误差会逐渐变得无界。虽然这在几年前是工业标准，但Ansys Fluent已经采取措施提供更高级的壁面处理方法，这些方法允许在不影响结果的情况下进行一致的网格细化。这种与$y^{\star }$无关的处理方法是所有基于$\omega$方程的湍流模型的默认设置。对于基于$\epsilon$方程的模型，Menter-Lechner和增强壁面处理（EWT）也起到了同样的作用。对$y^{+}$不敏感的壁面处理也是Spalart-Allmaras模型的默认设置，允许您在不受近壁面$y^{+}$分辨率影响的情况下运行该模型。

要获得高质量的壁面边界层数值结果，必须确保边界层的整体分辨率足够。实际上，这一要求比达到特定的 $y^{+}$ 值更为重要。准确覆盖边界层所需的最少单元数约为 10 个，但理想的数值是 20 个。还应注意的是，通过适度增加数值计算量，通常可以提高边界层分辨率，因为这仅需要对壁面法向方向进行网格细化。由此带来的精度提升通常非常值得额外的计算成本。对于非结构化网格，建议在壁面附近生成 10-20 层或更多的棱柱层，以准确预测壁面边界层。棱柱层的厚度应设计为确保实际覆盖边界层的节点数约为 15 个或更多。这可以在求解完成后通过查看湍流粘度来检查，湍流粘度在边界层中部达到最大值——这一最大值指示了边界层的厚度（最大值位置的两倍即为边界层边缘）。必须确保棱柱层厚度大于边界层，否则存在棱柱层限制边界层增长的风险。

4.18.1.2 建议：

• 对于基于 $\epsilon$ 方程的湍流模型：
  • 使用 Menter-Lechner (ML-ε) 或增强壁面处理 (EWT-ε)。
  • 如果倾向于使用壁面函数，选择可扩展壁面函数。
• 对于基于 $\omega$ 方程的湍流模型：
  • 默认的“相关性”已经提供了经过良好校准的 $y^{+}$ 不敏感壁面处理。
  • “表格化”的 $y^{+}$ 不敏感壁面处理为 BSL、SST 和 GEKO 提供了进一步的改进。
• 对于 Spalart-Allmaras 模型，使用默认的 $y^{+}$ 不敏感壁面处理。
• 对于大涡模拟 (LES)，使用基于 r+ 的谐波混合壁面函数（第 157 页）。

4.18.2 基于 $\epsilon$ 模型的壁面处理

对于基于 $\epsilon$ 的模型，以下壁面函数可供选择：

• 4.18.2.1 标准壁面函数
• 4.18.2.2 可扩展壁面函数
• 4.18.2.3 非平衡壁面函数
• 4.18.2.4 增强壁面处理 $\epsilon$ 方程 (EWT- $\epsilon$ )
• 4.18.2.5 Menter-Lechner $\epsilon$ 方程 (ML- $\epsilon$ )
• 4.18.2.6 用户自定义壁面函数

4.18.2.1 标准壁面函数

Ansys Fluent 中的标准壁面函数基于 Launder 和 Spalding [343]（第 1077 页）的工作，并在工业流动中得到最广泛的应用。它们作为默认选项在 Ansys Fluent 中提供。

4.18.2.1.1 动量

平均速度的壁面定律产生

$$U^{\ast }=\frac{1}{K}\ln \left(E{y}^{\ast }\right)\text{\hspace{1em}(4.338)}$$

何处

$$U^{\ast }\equiv \frac{U_P{C}_{\mu }^{1/4}{k}_P^{1/2}}{{\tau }_w/\rho }\text{\hspace{1em}(4.339)}$$

这是无量纲速度。

$$y^{\ast }\equiv \frac{\rho C_{\mu }^{1/4}{k}_P^{1/2}{y}_P}{\mu }\text{\hspace{1em}(4.340)}$$

这是从壁面起的无量纲距离。

以及

$\kappa =$ 冯·卡门常数 $\left(=0.4187\right)$

$E=$ 经验常数 $\left(=9.793\right)$

$U_P=$ 壁面相邻单元中心点 $P$ 处的流体平均速度

$k_P=$ 壁面相邻单元中心点 $P$ 处的湍流动能

$y_P=$ 壁面相邻单元中心点到壁面的距离，$P$

$\mu =$ 流体的动力粘度

壁函数适用的 $y^{\ast }$ 值范围取决于流动的整体雷诺数。下限通常在 $y^{\ast }\sim$ 15 左右。低于此限值时，壁函数通常会恶化，且解的准确性无法保持（例外情况见可扩展壁函数 (p. 143)）。上限则强烈依赖于雷诺数。对于非常高雷诺数的流动（例如船舶、飞机），对数层可延伸至数千的高值，而对于低雷诺数流动（例如涡轮叶片等），上限可能小至 100。对于这些低雷诺数流动，整个边界层通常仅为几百个 $y^{\ast }$ 单位。因此，应避免在这些流动中应用壁函数，因为它们限制了可以在边界层中合理布置的节点总数。一般而言，确保边界层覆盖有足够数量的（结构化）单元比确保某个 $y^{\ast }$ 值更为重要。

在Ansys Fluent中，当 $y^{\ast }>11.225$ 时，会采用对数律。而当网格使得壁面相邻单元处的 $y^{\ast }<11.225$ 时，Ansys Fluent则会应用层流应力-应变关系，该关系可以表示为

$$U^{\ast }=y^{\ast }\text{\hspace{1em}(4.341)}$$

需要注意的是，在Ansys Fluent中，平均速度和温度的壁面律基于壁面单位$y^{\ast }$，而不是$y^{+}\left(\equiv \rho u_{\tau }y/\mu \right)$。这些量在平衡湍流边界层中大致相等。

4.18.2.1.2 能量

雷诺关于动量和能量传输的类比给出了类似的平均温度对数律。与平均速度的壁面律一样，Ansys Fluent中采用的温度壁面律由以下两种不同的定律组成：

• 热传导子层或热粘性子层的线性律，其中传导起重要作用

• 湍流区域的对数律，其中湍流效应主导传导

热传导层的厚度通常与（动量）粘性子层的厚度不同，并且随流体不同而变化。例如，高普朗特数流体（如油）的热子层厚度远小于其动量子层厚度。相反，低普朗特数流体（如液态金属）的热子层厚度远大于动量子层厚度。

$$\frac{\delta }{{\delta }_T}\approx \sqrt{Pr}\text{\hspace{1em}(4.342)}$$

在高度可压缩流动中，由于粘性耗散引起的热效应，近壁区域的温度分布可能与低亚音速流动中的情况显著不同。在Ansys Fluent中，温度壁面函数考虑了粘性加热的影响[673] (第1096页)。

Ansys Fluent采用壁面缩放法，对无量纲温度实施了壁面定律：

$$T^{\ast }\equiv \frac{\left(T_w-T_p\right)\rho c_p{u}^{\ast }}{\dot{q}}=T_c^{\ast }+\frac{D}{\dot{q}},u^{\ast }=C_{\mu }^{1/4}{k}_p^{1/2}\text{\hspace{1em}(4.343)}$$

在此，我们采用以下复合形式对对流-传导部分 $T_c^{\ast }$ 和粘性加热部分 $D$ 进行建模：

$$T_c^{\ast }=\{\begin{array}{cc}\mathrm{Pr}{y}^{\ast }& y^{\ast }<y_T^{\ast }\\ \underset{t}{\mathrm{Pr}}\left[\frac{1}{\kappa }\ln \left(E{y}^{\ast }\right)+P\right]& y^{\ast }>y_T^{\ast }\end{array}\text{\hspace{1em}(4.344)}$$

$$D=\{\begin{array}{cc}\rho u^{\ast }\cdot \frac{1}{2}\mathrm{Pr}{U}_p^2& y^{\ast }<y_T^{\ast }\\ \rho u^{\ast }\cdot \frac{1}{2}\left[\underset{t}{\mathrm{Pr}}{U}_p^2+\left(\mathrm{Pr}-\underset{t}{\mathrm{Pr}}\right)U_c^2\right]& y^{\ast }>y_T^{\ast }\end{array}\text{\hspace{1em}(4.345)}$$

其中，$P$ 是根据 Jayatilleke [281]（第1073页）给出的公式计算得出的：

$$P=9.24\left[{\left(\frac{Pr}{P{r}_t}\right)}^{3/4}-1\right]\left[1+0.28e^{-0.007Pr/P{r}_t}\right]\text{\hspace{1em}(4.346)}$$

$k_P=$ 壁面相邻单元质心处的湍流动能

$\rho =$ 流体密度

$c_p=$ 流体比热容

$\dot{q}=$ 壁面热通量

$T_P=$ 壁面相邻单元质心处的温度

$T_w=$ 壁面温度

$Pr=$ 分子普朗特数 $\left(\mu c_p/k_f\right)$

$P{r}_t=$ 湍流普朗特数 (在壁面处为0.85)

$A=$ 范·德里斯特常数 $\left(=26\right)$

$U_c=$ 在 $y^{\ast }=y_T^{\ast }$ 处的平均速度大小

请注意，对于基于压力的求解器，这些项...

$$\frac{1}{2}\rho \mathrm{Pr}\frac{C_{\mu }^{1/4}{k}_P^{1/2}}{\dot{q}}{U}_P^2$$

以及

$$\frac{1}{2}\rho \frac{C_{\mu }^{1/4}{k}_P^{1/2}}{\dot{q}}\left\{\underset{t}{\mathrm{Pr}}{U}_P^2+\left(\underset{t}{\mathrm{Pr}}-\underset{t}{\mathrm{Pr}}\right)U_c^2\right\}$$

仅在可压缩流动计算中，方程4.343（第140页）会包含非维热子层厚度。

方程4.343（第140页）中的非维热子层厚度$y_{T^{\prime }}^{\ast }$，是根据所模拟流体的分子普朗特数，计算线性律与对数律相交处的$y^{\ast }$值得到的。

应用壁面律进行温度计算的步骤如下：一旦确定了所模拟流体的物理属性，就会计算其分子普朗特数。然后，根据分子普朗特数，通过线性分布与对数分布的交点计算热子层厚度$y_{T^{\prime }}^{\ast }$，并存储。

在迭代过程中，根据近壁单元格的$y^{\ast }$值，应用方程4.343（第140页）中的线性或对数分布来计算壁面温度$T_w$或热流$\dot{q}$（取决于热边界条件的类型）。

方程4.346（第140页）给出的$P$函数适用于光滑壁面。然而，对于粗糙壁面，该函数需作如下修改：

$$P_{\text{rough }}=3.15\stackrel{0.695}{\mathrm{Pr}}{\left(\frac{1}{E^{\prime }}-\frac{1}{E}\right)}^{0.359}+{\left(\frac{E^{\prime }}{E}\right)}^{0.6}P\text{\hspace{1em}(4.347)}$$

其中，$E^{\prime }$ 是针对粗糙壁面修正的壁面函数常数，由 $E^{\prime }=E/f_r$ 定义。若需了解粗糙度函数 $f_{r^{\prime }}$ 的描述，可参阅 Fluent 理论指南中的方程 4.413（第158页）。

4.18.2.1.3 物种

在使用物种传输的壁面函数时，Ansys Fluent 假设物种传输的行为类似于热传递。与方程 4.343（第140页）类似，对于无粘性耗散的常属性流动，壁面物种传输定律可表示为

$$Y^{\ast }\equiv \frac{\left(Y_{i,w}-Y_i\right)\rho C_{\mu }^{1/4}{k}_P^{1/2}}{J_{i,w}}=\{\begin{array}{cc}Sc{y}^{\ast }& \left(y^{\ast }<y_c^{\ast }\right)\\ S{c}_t\left[\frac{1}{\kappa }\ln \left(E{y}^{\ast }\right)+P_c\right]& \left(y^{\ast }>y_c^{\ast }\right)\end{array}\text{\hspace{1em}(4.348)}$$

其中，$Y_i$ 表示局部物种质量分数，$Sc$ 和 $S{c}_t$ 分别代表分子和湍流施密特数，而 $J_{i,w}$ 则是壁面上物种 $i$ 的扩散通量。需要注意的是，$P_c$ 和 $y_c^{\ast }$ 的计算方式与 $P$ 和 $y_{T^{\prime }}^{\ast }$ 类似，区别在于普朗特数始终被相应的施密特数所替代。

4.18.2.1.4 湍流

在 $k$ - $\epsilon$ 模型以及 RSM 中（如果启用了从 $k$ 方程获取壁面边界条件的选项），$k$ 方程在整个计算域内，包括邻近壁面的单元，都会被求解。壁面上施加的 $k$ 的边界条件为...

$$\frac{\partial k}{\partial n}=0\text{\hspace{1em}(4.349)}$$

其中，$n$ 是垂直于壁面的局部坐标。

在紧邻壁面的单元格中，动能 $G_k$ 的产生及其耗散率 $\epsilon$，作为 $k$ 方程的源项，是基于局部平衡假设进行计算的。在此假设下，$k$ 的产生及其耗散率在紧邻壁面的控制体积内被假定为相等。

因此，$k$ 的产生基于对数律，并由此计算得出。

$$G_k\approx {\tau }_w\frac{\partial U}{\partial y}={\tau }_w\frac{{\tau }_w}{\kappa \rho C_{\mu }^{1/4}{k}_P^{1/2}{y}_P}\text{\hspace{1em}(4.350)}$$

并且 $\epsilon$ 是由此计算得出的。

$${\epsilon }_P=\frac{C_{\mu }^{3/4}{k}_P^{3/2}}{\kappa y_P}\text{\hspace{1em}(4.351)}$$

在壁面相邻的单元中，不直接求解$\epsilon$方程，而是使用方程4.351（第142页）进行计算。$\omega$和雷诺应力方程则按照y+-Insensitive近壁处理（第152页）和壁面边界条件（第105页）中的详细说明进行求解。

需要注意的是，如这里所示，包括平均速度、温度、物种浓度、$k$和$\epsilon$在内的所有解变量的壁面边界条件，都由壁面函数处理。因此，您无需担心壁面的边界条件。

到目前为止描述的标准壁面函数在Ansys Fluent中作为默认选项提供。这些标准壁面函数对于广泛的壁面约束流动表现良好。然而，当流动情况偏离其在推导中假设的理想条件时，它们的可靠性往往会降低。其中，常剪切和局部平衡假设是最限制标准壁面函数通用性的因素。因此，当近壁流动受到严重压力梯度影响，或者流动处于强烈非平衡状态时，预测结果的质量可能会受到影响。

非平衡壁面函数作为附加选项提供，可能在这种情况下来改善结果。

[!重要] 标准壁面函数可用于以下粘性模型：

• $k-\epsilon$ 模型
• 雷诺应力模型

4.18.2.2 可扩展壁面函数

可扩展壁面函数避免了在网格细化至$y^{\ast }<11$时标准壁面函数的退化。这些壁面函数对于任意细化的网格都能产生一致的结果。对于比$y^{\ast }>11$更粗的网格，标准壁面函数是相同的。

可扩展壁面函数的目的在于，在标准壁面函数方法中强制使用对数律。这是通过在$y^{\ast }$计算中引入一个限制器来实现的，从而确保了这一点。

$${\tilde{y}}^{\ast }=\mathrm{MAX}\left(y\ast ,y{\ast }_{\text{limit }}\right)\text{\hspace{1em}(4.352)}$$

其中 $y{\ast }_{limit}=11.225$。在可扩展壁面函数概念中使用公式4.352（第143页）是直接的，即，任何标准壁面函数公式中使用的$y^{\ast }$形式被${\tilde{y}}^{\ast }$所取代。

可以在粘性模型对话框下的近壁面处理中启用可扩展壁面函数。

4.18.2.3 非平衡壁面函数

除了上述标准壁面函数（这是默认的近壁面处理）之外，还提供了一种基于两层的非平衡壁面函数[308]（第1075页）。非平衡壁面函数的关键元素如下：

• Launder和Spalding的平均速度对数律对压力梯度效应敏感。

• 采用基于两层的概念来计算壁面邻近单元中的湍流动能预算$\left(\overline{G_k},\bar{\epsilon }\right)$。

平均温度或物种质量分数的壁面律与上述标准壁面函数中的相同。

对压力梯度敏感的平均速度对数律是

$$\frac{\tilde{U}{C}_{\mu }^{1/4}{k}^{1/2}}{{\tau }_w/\rho }=\frac{1}{K}\ln \left(E\frac{\rho C_{\mu }^{1/4}{k}^{1/2}y}{\mu }\right)\text{\hspace{1em}(4.353)}$$

哪里

$$\tilde{U}=U-\frac{1}{2}\frac{dp}{dx}\left[\frac{y_v}{\rho \kappa \sqrt{k}}\ln \left(\frac{y}{y_v}\right)+\frac{y-y_v}{\rho \kappa \sqrt{k}}+\frac{y_v^2}{\mu }\right]\text{\hspace{1em}(4.354)}$$

而 $y_v$ 表示物理粘性子层厚度，其计算方法如下：

$$y_v\equiv \frac{\mu y_v^{\ast }}{\rho C_{\mu }^{1/4}{k}_P^{1/2}}\text{\hspace{1em}(4.355)}$$

其中，$y_v^{\ast }=11.225$。

非平衡壁面函数在计算壁面相邻单元中的湍流动能预算时采用了双层概念，这是为了求解壁面邻近单元中的$k$方程所必需的。壁面邻近单元被假定为包含粘性子层和完全湍流层。对于湍流量的分布，我们做出以下假设：

$${\tau }_t=\{\begin{array}{ll}0,& y<y_v\\ {\tau }_w,& y>y_v\end{array}k=\{\begin{array}{cc}{\left(\frac{y}{y_v}\right)}^2{k}_P,& y<y_v\\ k_P,& y>y_v\end{array}\epsilon =\{\begin{array}{ll}\frac{2vk}{y^2},& y<y_v\\ \frac{k^{3/2}}{C_t^{\ast }y},& y>y_v\end{array}\text{\hspace{1em}(4.356)}$$

其中，$C_{\ell }^{\ast }=\kappa C_{\mu }^{3/4}$，而$y_v$是粘性子层的无量纲厚度，定义在公式4.355（第143页）中。

利用这些分布，可以计算单元平均的$k$生成项$\overline{G_k}$和单元平均的耗散率$\bar{\epsilon }$，方法是对紧邻壁面的单元中的$G_k$和$\epsilon$进行体积平均。对于体积平均可以用深度平均近似的四边形和六面体单元，

$$\overline{G_k}\equiv \frac{1}{y_n}{\int }_0^{y_n}{\tau }_t\frac{\partial U}{\partial y}dy=\frac{1}{\kappa y_n}\frac{{\tau }_w^2}{\rho C_{\mu }^{1/4}{k}_P^{1/2}}\ln \left(\frac{y_n}{y_v}\right)\text{\hspace{1em}(4.357)}$$

以及

$$\bar{\epsilon }\equiv \frac{1}{y_n}{\int }_0^{y_n}\epsilon dy=\frac{1}{y_n}\left[\frac{2v}{y_v}+\frac{k_P^{1/2}}{C_{\ell }^{\ast }}\ln \left(\frac{y_n}{y_v}\right)\right]k_P\text{\hspace{1em}(4.358)}$$

其中，$y_n$ 是单元的高度（即 $y_n=2y_p$）。对于其他形状的单元（例如，三角形和四面体网格），则使用适当的体积平均值。

在公式 4.357（第 144 页）和公式 4.358（第 144 页）中，近壁单元湍流动能预算实际上取决于粘性子层和完全湍流层的比例，这在高度非平衡流动中随单元而异。非平衡壁面函数考虑了压力梯度对速度剖面畸变的影响。在这种情况下，当湍流动能的产生等于其破坏速率时的局部平衡假设不再有效。因此，非平衡壁面函数实际上部分考虑了在标准壁面函数中被忽略的非平衡效应。

4.18.2.3.1 标准壁面函数与非平衡壁面函数

由于能够部分考虑压力梯度的影响，非平衡壁面函数推荐用于涉及分离、再附着和冲击的复杂流动，其中平均流动和湍流受到压力梯度和快速变化的影响。在这样的流动中，可以获得改进，特别是在壁面剪切（皮肤摩擦系数）和热传递（努塞尔特或斯坦顿数）的预测中。

[!Important] 非平衡壁面函数可用于以下湍流封闭模型：

• $k-\epsilon$ 模型
• 雷诺应力输运模型

4.18.2.3.2 壁面函数方法的局限性

标准壁面函数对于大多数高雷诺数的有界壁面流动给出了合理的预测结果。非平衡壁面函数通过考虑压力梯度的影响，进一步扩展了壁面函数方法的适用性；然而，当流动条件与壁面函数所基于的理想条件偏离过多时，上述壁面函数的可靠性会降低。具体例子如下：

• 普遍存在的低雷诺数或近壁面效应（例如，通过小间隙的流动或高粘度、低速流体流动）。

• 通过壁面的大量渗透（吹/吸）。

• 导致边界层分离的严重压力梯度。

• 强大的体积力（例如，靠近旋转盘的流动，浮力驱动流动）。

• 近壁面区域的高度三维性（例如，Ekman 螺旋流动，强烈偏斜的 3D 边界层）。

如果您所模拟的流动中存在上述任何特征，并且对于模拟的成功至关重要，您必须采用近壁面建模方法，并在近壁面区域使用适当的网格分辨率。对于这种情况，Ansys Fluent 提供了增强壁面处理（适用于 $k$-$\epsilon$ 和 RSM 模型），以及 Menter-Lechner 近壁面处理（适用于 $k$-$\epsilon$ 模型）。

4.18.2.4 增强壁面处理 $\epsilon$ 方程 (EWT- $\epsilon$ )

增强壁面处理（Enhanced Wall Treatment）用于 $\epsilon$ 方程是一种近壁面建模方法，它结合了双层模型与所谓的增强壁面函数。如果近壁面网格足够精细，能够解析粘性子层（通常将第一个近壁面节点放置在 $y^{+}\approx 1$ 处），那么增强壁面处理将与传统的双层分区模型完全相同（详见下文）。然而，要求近壁面网格在所有地方都必须足够精细可能会导致过高的计算需求。理想情况下，我们希望有一种近壁面公式，既可以用于粗网格（通常称为壁面函数网格），也可以用于细网格（低雷诺数网格）。此外，对于那些第一个近壁面节点既不在完全湍流区域（适合使用壁面函数），也不在紧邻壁面处（$y^{+}\approx 1$，适合使用低雷诺数方法）的中间网格，不应产生过大的误差。

为了实现这一目标，即在近壁面网格精细时具有标准双层方法的精度，同时在壁面函数网格上不会显著降低精度，Ansys Fluent 可以将双层模型与增强壁面函数结合使用，具体描述如下。

4.18.2.4.1 增强壁面处理的双层模型

在 Ansys Fluent 的近壁面模型中，粘性影响的近壁面区域被完全解析至粘性子层。双层方法是增强壁面处理的重要组成部分，用于指定近壁面单元中的 $\epsilon$ 和湍流粘度。在这种方法中，整个域被细分为粘性影响区域和完全湍流区域。

区域。这两个区域的划分由基于壁面距离的湍流雷诺数 ${\mathrm{Re}}_y$ 决定，其定义为

$$R{e}_y\equiv \frac{\rho y\sqrt{k}}{\mu }\text{\hspace{1em}(4.359)}$$

其中，$y$ 是在单元中心计算的壁面法向距离。在 Ansys Fluent 中，$y$ 被解释为到最近壁面的距离：

$$y\equiv \underset{{\overrightarrow{r}}_w\in {\Gamma }_w}{\min }\Vert \begin{array}{c}\overrightarrow{r}-{\overrightarrow{r}}_w\end{array}\Vert \text{\hspace{1em}(4.360)}$$

其中，$\overrightarrow{r}$ 是场点的位置矢量，而 ${\overrightarrow{r}}_w$ 是壁面边界的位置矢量。${\Gamma }_w$ 是所有涉及的壁面边界的并集。这种解释使得 $y$ 能在涉及多个壁面的复杂形状流场中唯一地定义。此外，以这种方式定义的 $y$ 独立于网格拓扑结构。

在完全湍流区域 $\left(R{e}_y>R{e}_y^{\ast };R{e}_y^{\ast }=200\right)$，采用 $k-\epsilon$ 模型或 RSM（详见标准、RNG 和 Realizable $k-\epsilon$ 模型（第 49 页）以及雷诺应力模型（RSM）（第 96 页））。

在受粘性影响的近壁区域 $\left(R{e}_y<R{e}_y^{\ast }\right)$，采用 Wolfstein [716]（第 1098 页）的一方程模型。在一方程模型中，动量方程和 $k$ 方程保留，如标准、RNG 和 Realizable $\mathrm{k}-\epsilon$ 模型（第 49 页）以及雷诺应力模型（RSM）（第 96 页）所述。然而，湍流粘度 ${\mu }_t$ 的计算方式有所不同。

$${\mu }_{t,2\text{ layer }}=\rho C_{\mu }{\ell }_{\mu }\sqrt{k}\text{\hspace{1em}(4.361)}$$

在方程4.361（第146页）中出现的尺度长度，是根据[103]（第1062页）计算得出的。

$${\ell }_{\mu }=y{C}_{\ell }^{\ast }\left(1-e^{-R{e}_y/A_{\mu }}\right)\text{\hspace{1em}(4.362)}$$

上述针对湍流粘度的双层公式被用作增强壁面处理的一部分，其中双层定义与Jongen [284]（第1073页）提出的外区高雷诺数${\mu }_t$定义平滑地融合在一起。

$${\mu }_{t,\text{ enh }}={\lambda }_{\epsilon }{\mu }_t+\left(1-{\lambda }_{\epsilon }\right){\mu }_{t,\text{ 2layer }}\text{\hspace{1em}(4.363)}$$

在标准、RNG 和可实现 k-ε 模型（第 49 页）或雷诺应力模型（RSM）（第 96 页）中，${\mu }_t$ 是高雷诺数定义，适用于 $k$ -ε 模型或 RSM。定义了一个混合函数 ${\lambda }_{\epsilon }$，使得它在远离壁面时等于 1，而在壁面附近则为 0。该混合函数的形式如下：

$${\lambda }_{\epsilon }=\frac{1}{2}\left[1+\tanh \left(\frac{R{e}_y-R{e}_y^{\ast }}{A}\right)\right]\text{\hspace{1em}(4.364)}$$

常数 ( A ) 决定了混合函数的宽度。通过定义一个宽度，使得在给定 ( \Delta R e_y ) 的变化下，(\lambda_{\varepsilon}) 的值将在其远场值的 (1%) 范围内，从而得到结果。

$$A=\frac{\left|\Delta R{e}_y\right|}{\mathrm{artanh}\left(0.98\right)}\text{\hspace{1em}(4.365)}$$

通常，$\Delta R{e}_y$ 的取值范围在 $R{e}_y^{\ast }$ 的 5% 至 20% 之间。混合函数 ${\lambda }_{\epsilon }$ 的主要作用是防止当外层获得的 ${\mu }_t$ 值与粘性影响区域边缘由 Wolfstein 模型返回的 ${\mu }_t$ 值不匹配时，阻碍解的收敛。

在粘性影响区域中，$\epsilon$ 场的计算基于...

$$\epsilon =\frac{k^{3/2}}{{\ell }_{\epsilon }}\text{\hspace{1em}(4.366)}$$

方程4.366（第147页）中出现的长度尺度是根据Chen和Patel [103]（第1062页）计算得出的：

$${\ell }_{\epsilon }=y{C}_{\ell }^{\ast }\left(1-e^{-R{e}_y/A_{\epsilon }}\right)\text{\hspace{1em}(4.367)}$$

如果整个流动域都位于粘性影响区域内（即 $R{e}_y<200$），$\epsilon$ 不是通过求解输运方程获得的，而是通过方程 4.366（第 147 页）代数式获得的。为了确保内区域代数指定的 $\epsilon$ 与外区域通过求解输运方程获得的 $\epsilon$ 之间的平滑过渡，Ansys Fluent 采用了一种类似于 ${\mu }_t$ 混合的过程来混合 $\epsilon$。

方程 4.362（第 146 页）和方程 4.367（第 147 页）中的常数取自 [103]（第 1062 页），具体如下：

$$C_{\ell }^{\ast }=\kappa C_{\mu }^{-3/4},A_{\mu }=70,A_{\epsilon }=2C_{\ell }^{\ast }\text{\hspace{1em}(4.368)}$$

4.18.2.4.2 动量与能量方程的增强壁面处理

为了使一种方法能够适用于整个近壁区域（即粘性底层、缓冲层和完全湍流的外层区域），有必要将壁面定律表述为整个壁面区域的单一壁面定律。Ansys Fluent通过采用Kader [286]（第1073页）提出的函数，混合线性（层流）和对数（湍流）壁面定律来实现这一点：

$$u^{+}=e^{\Gamma }{u}_{lam}^{+}+e^{1/\Gamma }{u}_{turb}^{+}\text{\hspace{1em}(4.369)}$$

混合函数定义如下：

$$\Gamma =-\frac{a{\left(y^{+}\right)}^4}{1+b{y}^{+}}\text{\hspace{1em}(4.370)}$$

其中，$a=0.01$，$b=5$。

同样地，导数$\frac{d{u}^{+}}{d{y}^{+}}$的一般方程为

$$\frac{d{u}^{+}}{d{y}^{+}}=e^{\Gamma }\frac{d{u}_{lam}^{+}}{d{y}^{+}}+e^{1/\Gamma }\frac{d{u}_{turb}^{+}}{d{y}^{+}}\text{\hspace{1em}(4.371)}$$

这种方法使得完全湍流定律能够轻松地被修改和扩展，以考虑其他效应，如压力梯度或变量属性。该公式还保证了在大值和小值情况下$y^{+}$的正确渐近行为，并且在$y^{+}$落在壁面缓冲区（3< $y^{+}$ <10）的情况下，合理地表示速度剖面。

增强壁面函数是通过平滑地将对数层公式与层流公式混合而开发的。结合White和Cristoph [706]（第1098页）以及Huang等人 [260]（第1072页）的方法，推导出了具有热传递和压力梯度的可压缩流的增强湍流壁面定律。

$$\frac{d{u}_{turb}^{+}}{d{y}^{+}}=\frac{1}{\kappa y^{+}}{\left[S^{{}^{\prime }}\left(1-\beta u^{+}-\gamma {\left(u^{+}\right)}^{{}^2}\right)\right]}^{1/2}\text{\hspace{1em}(4.372)}$$

哪里

$$S^{\prime }=\{\begin{array}{ll}1+\alpha y^{+}& \text{for }{y}^{+}<y_s^{+}\\ 1+\alpha y_s^{+}& \text{for }{y}^{+}\ge y_s^{+}\end{array}\text{\hspace{1em}(4.373)}$$

以及

$$\alpha \equiv \frac{v_w}{{\tau }_w{u}^{\ast }}\frac{dp}{dx}=\frac{\mu }{{\rho }^2{\left(u^{\ast }\right)}^3}\frac{dp}{dx}\text{\hspace{1em}(4.374)}$$

$$\beta \equiv \frac{{\sigma }_t{q}_w{u}^{\ast }}{c_p{\tau }_w{T}_w}=\frac{{\sigma }_t{q}_w}{\rho c_p{u}^{\ast }{T}_w}\text{\hspace{1em}(4.375)}$$

$$\gamma \equiv \frac{{\sigma }_t{\left(u^{\ast }\right)}^2}{2c_p{T}_w}\text{\hspace{1em}(4.376)}$$

其中，$y_s^{+}$ 是确定对数律斜率的位置。默认情况下，$y_s^{+}=60$。方程4.372（第148页）中的系数$\alpha$表示压力梯度的影响，而系数$\beta$和$\gamma$则代表热效应。方程4.372（第148页）是一个常微分方程，Ansys Fluent将提供一个适当的解析解。如果$\alpha$、$\beta$和$\gamma$都等于0，解析解将导致经典的湍流对数壁面律。

层流壁面律由以下表达式确定：

$$\frac{d{u}_{lam}^{+}}{d{y}^{+}}=1+\alpha y^{+}\text{\hspace{1em}(4.377)}$$

请注意，上述表达式仅通过$\alpha$考虑了压力梯度的影响，而忽略了由于传热和可压缩性对层流壁面定律的变物性效应。这些效应被忽略是因为它们在靠近壁面处发生时被认为影响较小。对公式4.377（第148页）进行积分得到的结果为

$$u_{\text{lam }}^{+}=y^{+}\left(1+\frac{\alpha }{2}{y}^{+}\right)\text{\hspace{1em}(4.378)}$$

增强型热壁函数遵循了为速度剖面 $u^{+}$ 所开发的相同方法。统一的热壁公式根据Kader [286]（第1073页）的方法，将层流和对数分布进行了融合：

$$T^{+}\equiv \frac{\left(T_w-T_P\right)\rho c_p{u}^{\ast }}{\dot{q}}=e^{\Gamma }{T}_{\text{lam }}^{+}+e^{1/\Gamma }{T}_{\text{turb }}^{+}\text{\hspace{1em}(4.379)}$$

其中，$T_P$和$\dot{q}$的表示法与标准热壁函数（参见公式4.343（第140页））相同。此外，混合因子$\Gamma$定义为

$$\Gamma =-\frac{a{\left(\mathrm{Pr}{y}^{+}\right)}^4}{1+b\stackrel{3}{\mathrm{Pr}}{y}^{+}}\text{\hspace{1em}(4.380)}$$

其中，$Pr$ 表示分子普朗特数，系数 $a$ 和 $b$ 的定义如公式 4.370（第 147 页）所示。

除了公式 4.379（第 148 页）中关于 $T^{+}$ 的表述外，增强型热壁函数遵循与标准热壁函数相同的逻辑（参见能量（第 139 页）），从而得到湍流和层流热壁函数的以下定义：

$$T_{\text{lam }}^{+}=\mathrm{Pr}\left(u_{\text{lam }}^{+}+\frac{\rho u^{\ast }}{2\dot{q}}{u}^2\right)\text{\hspace{1em}(4.381)}$$

$$T_{turb}^{+}=P{r}_t\left\{u_{turb}^{+}+P+\frac{\rho u^{\ast }}{2\dot{q}}\left[u^2+\left(\frac{Pr}{P{r}_t}-1\right){\left(u_c^{+}\right)}^2{\left(u^{\ast }\right)}^2\right]\right\}\text{\hspace{1em}(4.382)}$$

其中，量 ( u_c^+ ) 是在层流和湍流区域之间假想的“过渡区”处 ( u^+ ) 的值。函数 ( P ) 的定义方式与标准壁面函数相同。

当使用增强壁面处理时，类似的程序也用于物种壁面函数。在这种情况下，方程4.381（第149页）和方程4.382（第149页）中的普朗特数被适当的施密特数所替代。有关物种壁面函数的详细信息，请参见物种（第141页）。

湍流动能的边界条件与标准壁面函数所使用的类似（方程4.349（第142页））。然而，湍流动能的生成 ( G_k ) 是使用与增强壁面律（方程4.369（第147页）和方程4.371（第147页））一致的速度梯度计算的，确保了在整个近壁区域都有效的公式。

[!重要] 增强壁面处理适用于所有 (\varepsilon) 方程模型（除了二次RSM模型）。 对于 ( k-\varepsilon ) 类型模型的另一种公式是Menter-Lechner处理，这是一种对 ( y^+ ) 不敏感的近壁处理。以下湍流模型默认应用 ( y^+ ) 不敏感的近壁处理：

• 所有 (\omega) 方程模型
• Spalart-Allmaras模型 请注意，对于Spalart-Allmaras模型和基于 (\omega) 方程的湍流模型的改进近壁处理，使用了与Kader混合不同的替代混合方法，这是新的默认近壁处理。

4.18.2.5 Menter-Lechner (\varepsilon) 方程（ML-(\varepsilon)）

历史上，有两种方法来模拟近壁流动：

• 壁面函数方法

• 低雷诺数模型

壁函数法要求第一个网格点的单元中心位于对数层内，而低雷诺数（low-Re）格式则需要以 $y^{+}<1$ 的分辨率积分至壁面。若在有效范围外使用这两种方法，都会产生较大误差。壁函数法在网格细化时效果会变差，而低雷诺数格式对于略粗于 $y^{+}=1$ 的网格，其计算得到的壁面剪应力（及热传递）值也不准确。为了给CFD用户提供对网格不那么敏感的格式，开发了不受 $y^{\ast }$ 影响的壁面模型。这意味着计算出的壁面值（剪应力和热传递）很大程度上与网格提供的 $y^{+}$ 值无关。任何对 $y^{+}$ 不敏感的壁面处理，在网格足够精细时会回归到其基础的低雷诺数格式，而在粗网格情况下则会采用壁函数法。对于 $\epsilon$ 方程的这类壁面处理，主要难点在于尚未有合适的低雷诺数格式。尽管已开发并发表了许多此类模型，但每种格式都存在以下一个或多个问题：

• 格式复杂，包含大量高度非线性的阻尼项。

• 对于复杂应用，数值上不够稳健。

• 对于同一应用，格式会产生多个解（即非唯一解）。

• 格式会产生“伪过渡”结果（即非物理的层流区）。

由于这些问题，当今工业代码中针对 $\epsilon$ 方程的模型制定选择了一种所谓的两层制定。它避免了在粘性子层中求解 $\epsilon$ 方程，而是用基于简单混合长度模型的代数形式来覆盖它。

在 Fluent 中，两层模型是增强壁面处理（EWT-ε）的基础，这是一种对所有基于 $\epsilon$ 方程的模型都具有 $y^{+}$ 不敏感性的制定。在两层方法中，流体域被划分为受粘性影响的区域和完全湍流区域。这两个区域的混合由湍流雷诺数 ${\mathrm{Re}}_y$ 决定（更多详情请参见增强壁面处理 $\epsilon$ 方程（EWT- $\epsilon$）（第145页））。

然而，使用湍流雷诺数 ${\mathrm{Re}}_y$ 来划分流动区域存在一些缺点：

• 湍流动能非常低的区域可能很容易具有小于200的湍流雷诺数。因此，这些区域即使远离壁面（例如，湍流水平非常低的区域），也会被采用近壁面制定来处理。

• Wolfstein 模型与非平衡（压力梯度）流动的 $\epsilon$ 方程不一致。因此，组合求解的结果依赖于切换位置。

• 对于网格较粗且在切换位置附近第一个单元格的 $y^{+}$ 较大的情况，模型在时间步之间来回切换时容易产生振荡。这种振荡会阻碍收敛。

为了避免这些缺点，Menter-Lechner近壁处理方法被开发出来，作为一种替代方案，它不基于两层方法。该方法还采用了一种新的低雷诺数（low-Re）公式，旨在避免现有$k$-$\epsilon$低雷诺数公式中存在的上述缺陷。

一个对$y^{+}$不敏感的近壁处理方法的目标是实现与$y^{+}$无关的壁面剪应力和壁面热通量的预测（假设边界层有足够的分辨率）。当网格细化时，该公式应逐渐从壁面函数过渡到低雷诺数公式。这还要求在粘性子层和对数区域之间对各种量进行混合。

4.18.2.5.1 动量方程

壁面剪应力${\tau }_w$作为边界条件是必需的，其计算公式为：

$${\tau }_w=\rho u^{\ast }{u}_{\tau }\text{\hspace{1em}(4.383)}$$

其中，$\rho$ 表示密度。摩擦速度 $(u_{\tau }$ 和 $u^{\ast })$ 在粘性子层和对数区之间进行了混合。以下公式用于混合 $u^{\ast }$：

$$u^{\ast }={\left[\left(\mu \left|\frac{\Delta U_{\tan }}{\Delta y}\right|+C_{\mu }^{1/2}\rho k\right)\frac{1}{\rho }\right]}^{1/2}\text{\hspace{1em}(4.384)}$$

对于摩擦速度 ( u_{\tau} )，我们采用以下公式：

$$u_{\tau }=U_{\tan }{\left[{\left(u_{\text{lam }}^{+}\right)}^{-4}+{\left(u_{\text{turb }}^{+}\right)}^{-4}\right]}^{1/4}\text{\hspace{1em}(4.385)}$$

4.18.2.5.2 k-ε 湍流模型

Menter-Lechner 近壁处理的主要思想是在湍流动能 $k$ 的输运方程中加入一个源项，以考虑近壁效应。标准 $k$ - $\epsilon$ 模型经过修改，如下列方程所示（为简化起见，未包括浮力效应）：

$$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)-\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]=G_k-\rho \epsilon +S_{\text{near-wall }}\text{\hspace{1em}(4.386)}$$

$$\frac{\partial }{\partial t}\left(\rho \epsilon \right)+\frac{\partial }{\partial x_i}\left(\rho \epsilon u_i\right)-\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial k}{\partial x_j}\right]=C_{1\epsilon }\frac{\epsilon }{k}{G}_k-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}\text{\hspace{1em}(4.387)}$$

$${\mu }_t=\rho C_{\mu }\frac{k^2}{\epsilon }\text{\hspace{1em}(4.388)}$$

其中，$C_{1\epsilon }=1.44,C_{2\epsilon }=1.92,C_{\mu }=0.09,{\sigma }_k=1.0$, 以及 ${\sigma }_{\epsilon }=1.3$。

额外的源项 $S_{\text{near-wall }}$ 仅在粘性子层中激活，用于考虑低雷诺数效应。它在对数区自动变为零。此源项的确切公式目前属于专有信息，因此在此不提供。

4.18.2.5.3 迭代改进

结合 Menter-Lechner 近壁面处理，对 $k$ - $\epsilon$ 两方程模型的迭代处理和线性化进行了改进。当使用此近壁面处理时，此修改默认激活。

Menter-Lechner 近壁面处理可与标准、可实现和 RNG $k$ - $\epsilon$ 湍流模型结合使用。

4.18.2.6 用户定义的壁面函数

此选项仅在启用 $k-\epsilon$ 模型时可用。在近壁面处理下选择用户定义的壁面函数，可以挂接一个壁面定律（Law-of-the-Wall）UDF。更多关于用户定义壁面函数的信息，请参阅 Fluent 定制手册中的 DEFINE_WALL_FUNCTIONS。

重要提示：

用户定义的壁面函数可用于 $k$ - $\epsilon$ 湍流封闭模型：

4.18.3 基于 $\omega$ 的湍流模型的 y++ 不敏感近壁面处理

在实施湍流模型时，近壁处理是一个关键点。设置壁边界条件有两个不同的分支，这取决于第一个近壁网格步长（参见图4.17：低和高雷诺数情况的计算网格（第152页））。第一个分支是低雷诺数公式（lowRe），其中第一个近壁网格步长位于边界层的粘性子层内（$y^{+}<5$）。第二个对应于高雷诺数（highRe）网格，其中激活了壁函数。在这种情况下，第一个近壁网格步长对应于对数分布（$y^{+}>30$）。在这两种情况之间，存在所谓的缓冲层。理想情况下，模拟应使用网格进行计算，其中$y^{+}$为1，然而这一要求并不总是容易实现，特别是在高雷诺数和复杂几何形状的工业计算中。也不总是可能在整个几何形状上创建纯壁函数网格，其中$y^{+}>30$。因此，开发了在这些极限之间平滑混合的壁公式。这样的公式被称为“$y^{+}$不敏感近壁处理”。

图4.17：低和高雷诺数情况的计算网格

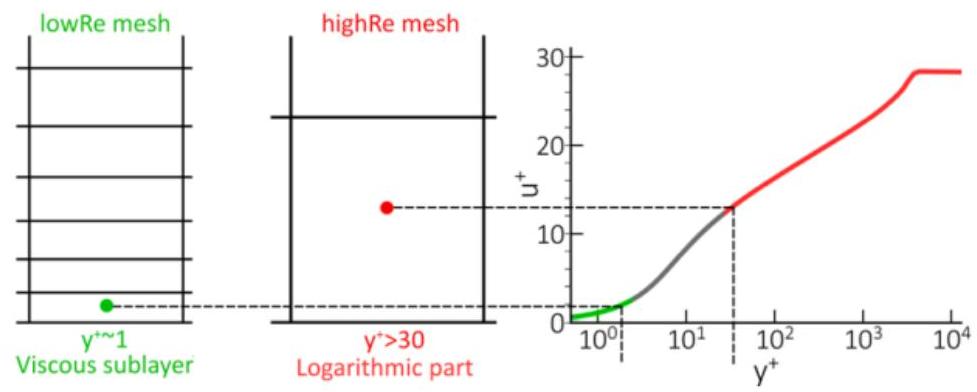
正如公式所暗示的，这些方法并非完全“$y^{+}$不敏感”，在缓冲层中通常会观察到与参考细网格解决方案相比，壁剪切应力值有轻微差异。

$y^{+}$ -insensitive near壁处理的目的是最小化这些变化，并开发壁边界条件，使得在假设边界层总体分辨率足够的情况下，解对近壁网格分辨率的敏感性尽可能小，特别是对于壁剪切应力和壁热流。

在基于$\omega$方程的湍流模型中，壁剪切应力由壁面指定的$\omega$值控制。在Ansys Fluent中，有两种$y^{+}$ -insensitive近壁处理方法可用：

• $\mathtt{correlation}$：根据$y^{+}$在粘性子层和对数区之间混合解析表达式（默认）。

• tabulated：采用表格查找壁面$\omega$值，以最小化两个区域之间的解析插值误差。

这两种方法均使用完全发展的平面Couette流动进行了校准，并将在以下章节中概述。除了对壁面$\omega$的处理外，其他量在网格细化时也需要从壁函数逐渐过渡到低Re数公式。

4.18.3.1 动量方程

壁剪切应力${\tau }_w$作为边界条件需要，并按以下方式计算：

$${\tau }_w=\rho u_{\tau }{u}^{\ast }\text{\hspace{1em}(4.389)}$$

其中，$\rho$ 表示密度。公式 4.389（第 153 页）基于摩擦速度 $u_{\tau }$ 和替代速度尺度 $u^{\ast }$，后者已被引入以改善分离区域的行为。这两个量在粘性子层和对数区之间进行了融合。

摩擦速度 $u_{\tau }$ 由以下公式给出：

$$u_{\tau }=\frac{U_{\text{tan }}}{{\left[{\left(u_{\text{lam }}^{+}\right)}^{-4}+{\left(u_{\text{turb }}^{+}\right)}^{-4}\right]}^{-1/4}}\text{\hspace{1em}(4.390)}$$

以下文本的中文翻译：

$$u_{\text{lam }}^{+}=y^{+}\text{\hspace{1em}(4.391)}$$

$$u_{\text{turb }}^{+}=\frac{1}{K}\ln \left[E\cdot \mathrm{MAX}\left(y^{+},0.2\right)\right]\text{\hspace{1em}(4.392)}$$

在给定的文本中，$\kappa =0.4187$ 和 $\mathrm{E}=9.793$，其中 $U_{\tan }$ 表示在靠近壁面的单元质心处，与壁面相切的平均速度。壁面无量纲距离 $y^{+}$ 是利用摩擦速度 $u^{\ast }$ 定义的：

$$y^{+}=\Delta y\frac{\rho u^{\ast }}{\mu }\text{\hspace{1em}(4.393)}$$

$\Delta y$ 表示紧邻壁面单元质心到壁面的距离，$\mu$ 表示分子粘度。

对于替代速度尺度 $u^{\ast }$ 的混合，采用以下公式：

$$u^{\ast }={\left[\left(\mu \left|\frac{\Delta U_{\tan }}{\Delta y}\right|+\left(C_{\mu }^{1/2}\rho k\right)\right)\frac{1}{\rho }\right]}^{1/2}\text{\hspace{1em}(4.394)}$$

其中，$\mathrm{k}$ 表示靠近壁面的单元质心处的湍流动能。

4.18.3.2 湍流

对于湍流动能的输运方程，不仅在对数区，而且在（人为地）向下积分至壁面的区域，都指定了零通量边界条件。壁面生成项在对数区和粘性子层之间进行了混合。生成项可以使用 $u^{+}$ 和 $y^{+}$ 以下列方式表示：

$$P_k={\mu }_t{\left(\frac{{\tau }_w}{\mu }\frac{\partial u^{+}}{\partial y^{+}}\right)}^2\text{\hspace{1em}(4.395)}$$

以下是粘性子层和对数区域的相应关系：

$$P_{k,lam}=\frac{\rho k}{\omega }{\left(\frac{{\tau }_w}{\mu }\right)}^2\text{\hspace{1em}(4.396)}$$

$$P_{k,\text{ turb }}=\frac{{\tau }_w^2}{\mu }\frac{\partial u_{\text{turb }}^{+}}{\partial y^{+}}\text{\hspace{1em}(4.397)}$$

请注意，$\partial u_{turb}^{+}/\partial y^{+}$并非基于梯度计算，而是直接从第4.392式（第153页）的对数律关系中推导得出。

最终，壁面生成项的混合形式表述如下：

$$P_{k,\text{ wall }}={\left(P_{k,\text{ lam }}^{-1}+P_{k,\text{ turb }}^{-1}\right)}^{-1}\text{\hspace{1em}(4.398)}$$

在比耗散率的输运方程中，壁面处的$\omega$值是预先设定的。壁面值通过以下方式在粘性子层和对数区之间的关系之间进行混合：

$${\omega }_{\mathrm{wall}}=\frac{\rho {\left(u^{\ast }\right)}^2}{\mu }{\omega }_{\mathrm{wall}}^{+}\text{\hspace{1em}(4.399)}$$

其中，$\rho$ 和 $\mu$ 分别表示密度和动力粘度。${\mathbf{u}}^{\ast }$ 代表在公式 4.394（第 153 页）中给出的替代速度尺度。

对于层流底层和对数区域，可以给出 ${\omega }_{wall}^{+}$ 的解析解。这种策略可以用来定义一个对 $y^{+}$ 不敏感的近壁面处理方法，通过根据 $y^{+}$ 在这两种解析表达式之间进行混合：

$${\omega }_{\text{wall }}^{+}={\omega }_{\text{lam }}^{+}\cdot {\left[1+{\left(\frac{{\omega }_{\text{turb }}^{+}}{{\omega }_{\text{lam }}^{+}}\right)}^{C_{\exp }}\right]}^{1/C_{\exp }}\text{\hspace{1em}(4.400)}$$

$${\omega }_{\text{lam }}^{+}=\frac{C_{\text{calib }}\cdot 6}{{\beta }_i{\left(y^{+}\right)}^2}\text{\hspace{1em}(4.401)}$$

$${\omega }_{\text{turb }}^{+}=\frac{1}{\sqrt{{\beta }_{\infty }^{\ast }}}\cdot \frac{d{u}_{\text{turb }}^{+}}{d{y}^{+}}\text{\hspace{1em}(4.402)}$$

这种表述是目前在Ansys Fluent中的默认处理方式，后续将称之为"关联法"。为了使壁面剪切应力在$y^{+}$上的变化最小化，我们采用了雷诺数为${10}^6$的不可压缩平面库埃特流动来校准整个动量和湍流方程的表述。这导致${\mathrm{C}}_{\text{calib }}$的值为$1/3$，${\mathrm{C}}_{\exp }$的值为1.3。然而，由于其分析表达式，这种表述仅提供了有限的微调可能性。

通过为${\omega }_{wall}^{+}$使用广泛的$y^{+}$值的表格查找，我们实现了进一步的改进。同样，我们再次使用不可压缩平面库埃特流动来校准这种表述，以使壁面剪切应力在$y^{+}$上的变化最小化。为此，我们创建了一个精细网格的解，并将得到的壁面剪切应力作为粗网格的参考。通过运行平面库埃特流动的各种网格，存储最佳的${\omega }_{\text{wall }}$，然后将获得的数据集转换为${\omega }_{\text{wall }}^{+}$的高效表格查找，我们创建了一个表格。

我们为BSL、SST和GEKO湍流模型创建了特定的表格，这种方法后续将标记为"表格化"。所有其他基于$\omega$的湍流模型都在使用SST表格查找，例如，Transition SST、DES-SST和SAS-SST（都作为独立模型实现）都在使用一致的表格。

对于高质量网格且$y+$值较小（$y+<1$）以及适度扩张比的网格，两种公式吻合良好。尽管这些网格通常被推荐使用，但由于应用的复杂性，可能并非总能创建这样的网格。表格查找提供了更准确的壁面剪切应力预测，尤其是对于$y+$值较大和/或扩张比较高的较差网格。

作为一个改进的例子，下面展示了零压力梯度平板边界层流动的结果。该设置基于Wieghardt & Tillmann的实验[783]（第1102页），基于入口速度和平板长度的雷诺数为$Re=10^7$。图4.18（第155页）显示了使用SST湍流模型计算的精细网格（$y+\sim 0.1$，左侧）和粗糙网格（$y+\sim 22$，右侧）在“相关性”和“表格化”近壁处理下的皮肤摩擦分布。两种公式的视觉差异很小，证实了相关性模型已经相当接近。

图4.18：使用SST模型在精细（$y+\sim 0.1$，左侧）和粗糙（$y+\sim 22$，右侧）网格上，“相关性”和“表格化”近壁处理的皮肤摩擦分布比较。

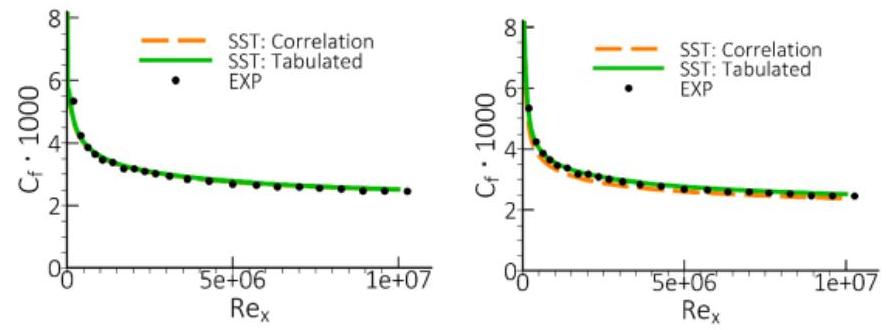
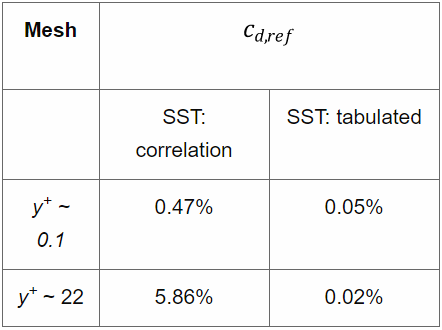
然而，从整体阻力来看，“表格化”（新）模型在本例中表现更优。阻力预测的误差定义为...

$$c_{d,\text{ error }}=\frac{c_d-c_{d,\text{ ref }}}{c_{d,\text{ ref }}}\text{\hspace{1em}(4.403)}$$

参考解 $c_{d,ref}$ 对应于在非常细的网格上得到的解，其中 y+ 约为 0.001。结果总结在表 1 中，可以看出，对于“表格化”近壁处理，粗网格上的误差显著减小。

表 4.3：在细网格（y+ ≈ 0.1）和粗网格（y+ ≈ 22）上，相对于（y+ ≈ 0.001）网格，使用 SST 模型的“相关性”和“表格化”近壁处理的阻力预测误差。

4.18.3.3 能量

能量方程的近壁处理采用 Kader 混合方法，介于粘性子层和壁面对数律之间，如公式 4.379（第 148 页）所述。

4.18.3.4 限制

• 对于表格化选项，有专门为 BSL、SST 和 GEKO 校准的表格。所有其他基于 omega 的湍流模型都使用 SST 表格查找，例如，Transition SST、DES-SST 和 SAS-SST（均作为单独模型实现）使用一致的表格查找。

• 这两种公式也可以与标准粗糙度模型结合使用。

注意：

高粗糙度（结冰）模型仅在 y+ ≈ 1 的网格上工作，并使用单独的近壁处理，适用于指定位置的壁面。

4.18.4 LES 近壁处理

对于 LES 模型，以下壁面函数可用：

• 4.18.4.1 Kader 混合壁面函数
• 4.18.4.2 基于 $\mathrm{r}+$ 的谐波混合壁面函数
• 4.18.4.3 Werner 和 Wengle 壁面处理

4.18.4.1 Kader 混合壁面函数

Kader [286]（第 1073 页）广泛使用的层流子层和对数律混合是 Fluent 中的默认选项。

当网格足够细以解析层流子层时，壁面剪应力从层流应力-应变关系中获得：

$$\frac{\bar{u}}{u_{\tau }}=\frac{\rho u_{\tau }y}{\mu }\text{\hspace{1em}(4.404)}$$

如果网格过于粗糙，无法解析层流底层，则假定与壁面相邻的单元中心位于边界层的对数区域，并采用壁面律：

$$\frac{\bar{u}}{u_{\tau }}=\frac{1}{K}\ln E\left(\frac{\rho u_{\tau }y}{\mu }\right)\text{\hspace{1em}(4.405)}$$

其中，$\kappa$ 是冯·卡门常数，$E=9.793$。如果网格使得第一个近壁点位于缓冲区内部，则根据公式 4.369（第 147 页）将上述两种定律进行混合。

4.18.4.2 基于 r+ 的调和混合壁面函数

经典的壁面定律公式形式如下：

$$u^{+}=f\left(y^{+}\right)\text{\hspace{1em}(4.406)}$$

此方程将未知剪切速度 $u_{\tau }$ 与近壁面单元中心的已知量 $\mathrm{u}$、$\mathrm{y}$ 和 $\nu$ 联系起来。为了计算 $u_{\tau }$，需要进行迭代，而显式公式则基于一个不包含 $u_{\tau }$ 的替代变量：

$$r^{+}=\frac{uy}{v}\text{\hspace{1em}(4.407)}$$

粘性次层公式：

$$u_{sub}^{+}=\sqrt{r^{+}}\text{\hspace{1em}(4.408)}$$

日志层公式化：

$$u_{\log }^{+}=C_1\ln \left(r^{+}+C_2\right)\text{\hspace{1em}(4.409)}$$

采用 $C_1=2.21$，$C_2=4$。

为了使粘性子层与对数层平滑过渡，采用了调和幂律：

$$u^{+}\left(r^{+}\right)={\left[{\left(u_{\text{sub }}^{+}\right)}^{-\alpha }+{\left(u_{\log }^{+}\right)}^{-\alpha }\right]}^{-\frac{1}{\alpha }}\text{\hspace{1em}(4.410)}$$

具有指数 $\alpha =6$ 的调和混合壁函数。

可以从粘性模型面板（如《Fluent 用户指南》中设置大涡模拟模型所述）启用调和混合壁函数，或使用以下文本命令：

define/models/viscous/near-wall-treatment/harmonic-blend-rplus-wf?

与 LES 可用的其他壁处理选项不同，基于 $r^{+}$ 的壁函数支持包括壁粗糙度效应（参见湍流壁边界流动中的壁粗糙度效应（第 158 页））。

注意：

在使用基于 $r^{+}$ 的调和混合壁函数与粗糙壁面结合时，为了保持粗糙度对流动的完整影响，请确保网格满足要求 $y_1>k_s$ 。

4.18.4.3 Werner 和 Wengle 壁处理

在 Ansys Fluent 的 LES 模拟中，有一种基于 Werner 和 Wengle [702]（第 1097 页）工作的替代近壁方法，他们提出了对近壁速度分布的幂律进行解析积分，从而得到以下壁面剪应力的表达式：

$$\left|{\tau }_w\right|=\{\begin{array}{ll}\frac{2\mu |u_p|}{\Delta z}& \text{ for }\left|u_p\right|\le \frac{\mu }{2\rho \Delta z}{A}^{\frac{2}{1-B}}\\ \rho {\left[\frac{1-B}{2}{A}^{\frac{1+B}{1-B}}{\left(\frac{\mu }{\rho \Delta z}\right)}^{1+B}+\frac{1+B}{A}{\left(\frac{\mu }{\rho \Delta z}\right)}^B\left|u_p\right|\right]}^{\frac{2}{1+B}}& \text{ for }\left|u_p\right|>\frac{\mu }{2\rho \Delta z}{A}^{\frac{2}{1-B}}\end{array}\text{\hspace{1em}(4.411)}$$

其中，$u_p$ 是与墙壁平行的速度，$A=8.3$，$B=1/7$ 是常数，$\Delta z$ 是近壁控制体积的长度尺度。

可以通过使用 define/models/viscous/near-wall-treatment/werner-wengle-wall-fn? 文本命令来启用 Werner-Wengle 壁面函数。

4.18.5 湍流壁边界流动中的壁面粗糙度效应

在粗糙管道和通道中的实验表明，当以通常的半对数尺度绘制时，粗糙壁附近的平均速度分布具有相同的斜率（即 $\left(1/\kappa \right)$），但截距不同（对数定律中的附加常数 $B$）。因此，针对粗糙度修正的平均速度壁面定律具有以下形式：

$$\frac{u_p{u}^{\ast }}{{\tau }_w/\rho }=\frac{1}{K}\ln \left(E\frac{\rho u^{\ast }{y}_p}{\mu }\right)-\Delta B\text{\hspace{1em}(4.412)}$$

其中，$u^{\ast }=C_{\mu }^{1/4}{k}^{1/2}$

$$\Delta B=\frac{1}{K}\ln f_r\text{\hspace{1em}(4.413)}$$

其中，$f_r$ 是一个粗糙度函数，用于量化由于粗糙度效应导致的截距偏移。

对于基于 $r^{+}$ 的 LES 壁面函数（参见基于 $\mathrm{r}+$ 的谐波混合壁面函数（第 157 页）），在粗糙壁面上，使用以下公式对对数部分进行偏移：

$$u_{\log }^{+}=C_1\ln \left[r^{+}+\frac{\Delta B}{u_{\log }^{+}}{r}^{+}+C_2\right]-\Delta B\text{\hspace{1em}(4.414)}$$

通常，$\Delta B$ 取决于粗糙度的类型（均匀沙粒、铆钉、线材、肋条、网线等）和尺寸。没有一种通用的粗糙度函数适用于所有类型的粗糙度。然而，对于沙粒粗糙度和类似类型的均匀粗糙元素，发现 $\Delta B$ 与无量纲粗糙度高度 $K_s^{+}=\rho K_s{u}^{\ast }/\mu$ 有很好的相关性，其中 $K_s$ 是物理粗糙度高度，$u^{\ast }=C_{\mu }^{1/4}{k}^{1/2}$。对实验数据的分析表明，粗糙度函数不是 $K_s^{+}$ 的单一函数，而是根据 $K_s^{+}$ 的值呈现不同的形式。观察到存在三个不同的区域：

• 水动力学光滑区 $\left(K_s^{+}\le 2.25\right)$

• 过渡区 $\left(2.25<K_s^{+}\le 90\right)$

• 完全粗糙区 $\left(K_s^{+}>90\right)$

根据数据，粗糙度效应在水动力学光滑区可以忽略不计，但在过渡区变得日益重要，并在完全粗糙区完全生效。

在 Ansys Fluent 中，整个粗糙度区域被细分为这三个区域，并采用基于 Nikuradse 数据 [98]（第 1062 页）的 Cebeci 和 Bradshaw 提出的公式来计算每个区域的 $\Delta B$。

对于水动力学光滑区 $\left(K_s^{+}\le 2.25\right)$：

$$\Delta B=0\text{\hspace{1em}(4.415)}$$

对于过渡状态 $\left(2.25<K_s^{+}\le 90\right)$ :

$$\Delta B=\frac{1}{K}\ln \left[\frac{K_s^{+}-2.25}{87.75}+C_s{K}_s^{+}\right]\times \sin \left\{0.4258\left(\ln K_s^{+}-0.811\right)\right\}\text{\hspace{1em}(4.416)}$$

其中，$C_s$ 是一个粗糙度常数，其值取决于粗糙度的类型。

在完全粗糙区域 $\left(K_s^{+}>90\right)$ 内：

$$\Delta B=\frac{1}{K}\ln \left(1+C_s{K}_s^{+}\right)\text{\hspace{1em}(4.417)}$$

在求解器中，给定粗糙度参数后，$\Delta B\left(K_s^{+}\right)$ 通过相应的公式（公式4.415（第159页）、公式4.416（第159页）或公式4.417（第159页））进行评估。然后，使用公式4.412（第158页）中的修正壁面律来评估壁面剪应力以及平均温度和湍流量的其他壁面函数。

$\Delta B\left(K_s^{+}\right)$ 表示对数速度剖面的向下偏移，如下图所示：

图4.19：对数速度剖面的向下偏移

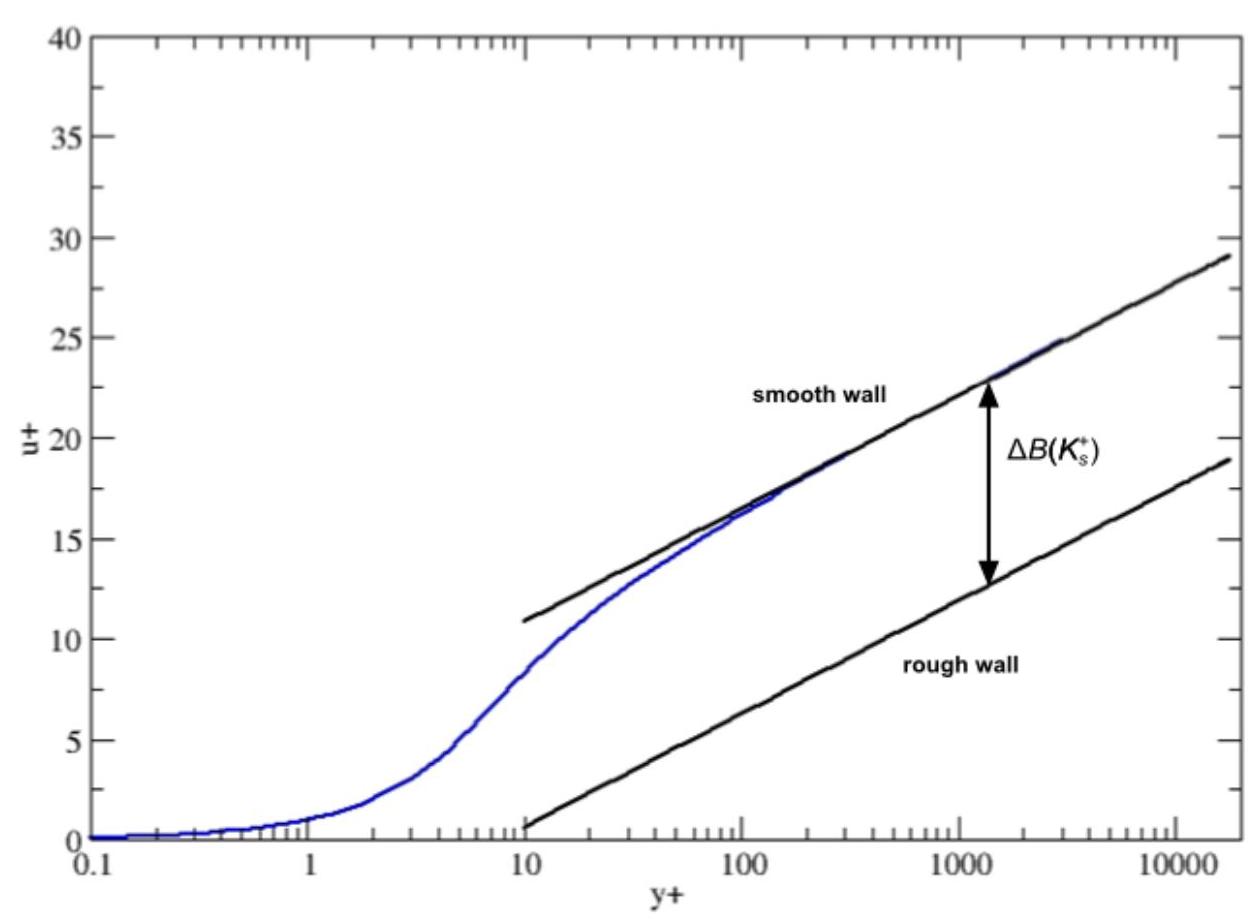
这种向下偏移会导致粗糙度高度较大且 $y^{+}$ 值较低时出现奇点。根据湍流模型和近壁处理方式，Ansys Fluent 采用了两种不同的方法来避免这一问题：

• 随着 $y^{+}$ 减小，降低粗糙度高度

第一种方法基于网格细化重新定义粗糙度高度：

$$K_s^{+}=\min \left(K_s^{+},y^{+}\right)\text{\hspace{1em}(4.418)}$$

这确保了当 $y^{+}$ 趋近于零时，$K_s^{+}$ 也同样趋近于零。因此，在这种情况下，为了保持粗糙度对流动的全部影响，粗糙壁面的网格要求是 $y^{+}>K_s^{+}$。

• 虚拟移动壁面

第二种方法基于以下观察：粘性子层仅在液压光滑壁附近完全建立。在过渡粗糙度区域，粗糙元件略厚于粘性子层并开始干扰它，因此在完全粗糙流动中，子层被破坏，粘性效应变得可忽略不计。下图用一层紧密排列的球体表示等效砂粒粗糙度，这些球体的平均粗糙度高度代表具有不同形状和大小的峰谷的技术粗糙度（参见 Schlichting 和 Gersten [578]（第 1090 页））：

图 4.20：等效砂粒粗糙度示意图

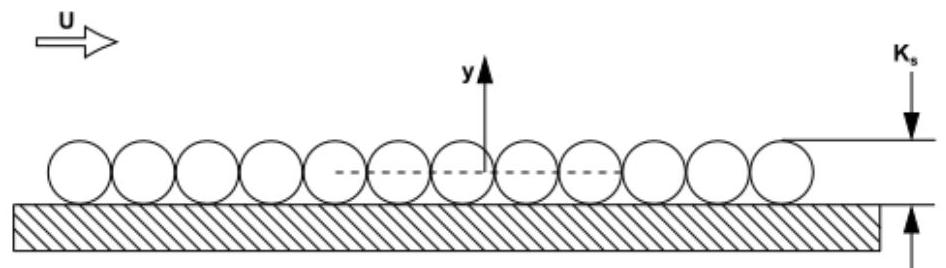
可以假设粗糙度具有约为其高度 50% 的阻塞效应（注意上图显示了三维排列的二维截面）。

因此，将壁面虚拟移动到粗糙元件高度的 50% 是合理的。这导致第一个单元中心的修正 $y^{+}$ 值：

$$y^{+}=y^{+}+K_s^{+}/2\text{\hspace{1em}(4.419)}$$

这种方法能够大致给出由表面粗糙度引起的正确位移。因此，奇点问题得以避免，细网格也能被正确处理。

第二种方法（即虚拟移动壁面）是基于$\omega$方程的所有两方程湍流模型以及以下基于$\epsilon$方程的湍流模型处理粗糙壁面的默认处理方式，当它们与标准和可扩展壁面函数一起使用时（注意，推荐使用可扩展壁面函数而不是标准壁面函数）：

• 标准、RNG 和 realizable $k-\epsilon$ 模型
• 雷诺应力模型

所有其他与粗糙壁面结合的模型组合（例如，Spalart-Allmaras 模型和 LES 结合基于$\mathrm{r}+$的谐波混合壁面函数（第157页））在细网格上没有特殊校准，因此使用第一种方法（随着$y^{+}$减小降低粗糙度高度）。

[!Note] 与随着$y^{+}$减小降低粗糙度高度（公式4.418（第160页））相比，使用虚拟壁面移动（公式4.419（第161页））处理粗糙壁面的优势在于，它消除了壁面附近网格分辨率的所有限制，因此可以在任意细网格上使用。

[!Important] 在Ansys Fluent 14之前，当使用基于$\epsilon$方程的湍流模型时，并未应用公式4.419（第161页）所描述的移动。您可以通过使用以下方案命令恢复先前的代码行为：(rpsetvar 'ke-rough-wall-treatment-r14? #f) (models-changed)