本节介绍大涡模拟（LES）模型的理论基础。相关信息将在以下章节中呈现：

4.16.1. 概述

4.16.2. 亚格子尺度模型

4.16.3. 尺度解析模拟的入口边界条件

关于在Ansys Fluent中使用该模型的详细信息，请参阅用户指南中的“湍流建模”和“设置大涡模拟模型”部分。

4.16.1 概述

湍流流动的特点是存在各种长度和时间尺度的涡流。最大的涡流通常与平均流动的特征长度相当（例如，剪切层厚度）。最小的尺度负责湍流动能的耗散。

理论上，可以使用一种称为直接数值模拟（DNS）的方法直接解析整个湍流尺度谱。在DNS中不需要建模。然而，对于涉及高雷诺数流动的实际工程问题，DNS并不可行。DNS解析整个尺度范围所需的成本与$R{e}_t^3$成正比，其中$R{e}_t$是湍流雷诺数。显然，对于高雷诺数，成本变得过高。在大涡模拟（LES）中，大涡流被直接解析，而小涡流则被建模。因此，LES在解析尺度的比例上介于DNS和RANS之间。LES的基本原理可以概括如下：

• 动量、质量、能量和其他被动标量主要由大涡流输送。

• 大涡流更依赖于具体问题。它们受流动的几何形状和边界条件的影响。

• 小涡流对几何形状的依赖性较小，趋于更加各向同性，因此更具普遍性。 找到一个适用于所有湍流尺度的普适模型，在小尺度涡旋中概率更高。

仅解析大尺度涡旋使得在LES（大涡模拟）中可以使用比DNS（直接数值模拟）更粗糙的网格和更大的时间步长。然而，LES仍然需要比通常用于RANS（雷诺平均Navier-Stokes）计算更细的网格。此外，LES需要运行足够长的流动时间以获得所模拟流动的稳定统计数据。因此，就内存（RAM）和CPU时间而言，LES的计算成本通常比稳态RANS计算高出几个数量级。因此，高性能计算（例如，并行计算）对于LES是必要的，特别是在工业应用中。LES的主要缺点在于壁面边界层的高分辨率要求。在壁面附近，即使是“大”涡旋也变得相对较小，并且需要依赖雷诺数的分辨率。这限制了LES在壁面约束流动中的应用，使其仅适用于非常低的雷诺数（Re $\sim {10}^4$ – ${10}^5$）和有限的计算域。

以下章节详细介绍了LES的控制方程、亚格子尺度湍流模型以及边界条件。

4.16.2 亚格子尺度模型

由于过滤操作产生的亚格子尺度（SGS）应力是未知的，需要进行建模。Ansys Fluent中的亚格子尺度湍流模型采用了与RANS模型相同的Boussinesq假设[247]（第1071页），通过计算亚格子尺度湍流应力来实现。 $${\tau }_{ij}-\frac{1}{3}{\tau }_{kk}{\delta }_{ij}=-2{\mu }_t{\bar{S}}_{ij}\text{\hspace{1em}(4.298)}$$ 其中，${\mu }_t$ 表示亚格子尺度湍流粘性。亚格子尺度应力 ${\tau }_{kk}$ 的各向同性部分未被建模，而是添加到过滤后的静压项中。${\bar{S}}_{ij}$ 是定义为解析尺度应变率张量。 $${\bar{S}}_{ij}\equiv \frac{1}{2}\left(\frac{\partial {\bar{u}}_i}{\partial x_j}+\frac{\partial {\bar{u}}_j}{\partial x_i}\right)\text{\hspace{1em}(4.299)}$$ 对于可压缩流体，引入密度加权的（或称为Favre）滤波操作符较为便利： $$\tilde{\phi }=\frac{\overline{\rho \phi }}{\bar{\rho }}\text{\hspace{1em}(4.300)}$$ Favre滤波后的Navier-Stokes方程与公式4.9（第43页）具有相同的形式。亚格子应力张量的可压缩形式定义如下： $${\tau }_{ij}=\bar{\rho }{u}_i{\tilde{u}}_j-\bar{\rho }{\tilde{u}}_i{\tilde{u}}_j\text{\hspace{1em}(4.301)}$$ 这个术语被分解为各向同性部分和偏量部分。 $${\tau }_{ij}=\underset{\text{deviatoric }}{\underbrace{{\tau }_{ij}-\frac{1}{3}{\tau }_{kk}{\delta }_{ij}}}+\underset{\text{isotropic }}{\underbrace{\frac{1}{3}{\tau }_{kk}{\delta }_{ij}}}\text{\hspace{1em}(4.302)}$$ 亚网格尺度应力张量的偏差部分采用可压缩形式的Smagorinsky模型进行建模： $${\tau }_{ij}-\frac{1}{3}{\tau }_{kk}{\delta }_{ij}=-2{\mu }_t\left(S_{ij}-\frac{1}{3}{S}_{kk}{\delta }_{ij}\right)\text{\hspace{1em}(4.303)}$$ 对于不可压缩流动，涉及 ${\tau }_{kk}$ 的项可以加到过滤后的压力上，或者直接忽略不计 [165]（第1066页）。实际上，这一项可以重写为 ${\tau }_{kk}=\gamma M^{2}sgs\bar{p}$，其中 $M_{sgs}$ 是次网格马赫数。当流动的湍流马赫数较小时，可以预期这个次网格马赫数也会很小。

Ansys Fluent 提供了四种 ${\mu }_t$ 模型：Smagorinsky-Lilly 模型、动态 Smagorinsky-Lilly 模型、WALE 模型和动态动能次网格尺度模型。

标量 $\phi$ 的次网格尺度湍流流，是通过使用次网格尺度湍流普朗特数来建模的。 $$q_j=-\frac{{\mu }_t}{{\sigma }_t}\frac{\partial \phi }{\partial x_j}\text{\hspace{1em}(4.304)}$$ 其中，$q_j$ 表示次网格尺度通量。

可压缩次网格焓通量项采用相同方式建模： $$\bar{\rho }\left(\widetilde{u_i{h}_s}-{\tilde{u}}_i{\tilde{h}}_s\right)=-\frac{{\mu }_{\mathrm{SGS}}{C}_p}{\underset{\mathrm{SGS}}{\mathrm{Pr}}}\frac{\partial \tilde{T}}{\partial x_j}\text{\hspace{1em}(4.305)}$$ 其中，$h_s$ 表示显焓，${\mu }_{\mathrm{SGS}}$ 是亚格子粘度，而 $\underset{\mathrm{SGS}}{\mathrm{Pr}}$ 是一个等于 0.85 的亚格子普朗特数。

在动态模型中，亚格子尺度湍流普朗特数或施密特数是通过将Germano [199]（第1068页）最初提出的动态过程应用于亚格子尺度通量来获得的。

4.16.2.1 Smagorinsky-Lilly 模型

这个简单的模型最初由 Smagorinsky [603]（第1092页）提出。在 Smagorinsky-Lilly 模型中，涡粘性是由... $${\mu }_t=\rho L_s^2\left|\bar{S}\right|\text{\hspace{1em}(4.306)}$$ 其中，$L_s$ 表示亚格子尺度的混合长度，而 $\left|\bar{S}\right|\equiv \sqrt{2{\bar{S}}_{ij}{\bar{S}}_{ij}}$。在 Ansys Fluent 中，$L_s$ 的计算采用 $$L_s=\min \left(\kappa d,C_s\Delta \right)\text{\hspace{1em}(4.307)}$$ 其中，$\kappa =0.41$ 是冯·卡门常数，$d$ 是到最近壁面的距离，$C_s$ 是Smagorinsky常数，而 $\Delta$ 是局部网格尺度。在Ansys Fluent中，$\Delta$ 是根据计算单元的体积来计算的。 $$\Delta =V^{1/3}\text{\hspace{1em}(4.308)}$$ Lilly 在惯性子区内的均匀各向同性湍流中，为 $C_s$ 得出了一个 0.23 的值。然而，在存在平均剪切和靠近固体边界等过渡流中，这一数值被发现会导致大尺度波动的过度阻尼，因此在这些区域需要降低。简而言之，$C_s$ 并非一个普适常数，这是这一简单模型的最严重缺陷。尽管如此，在广泛的流动范围内，$C_s$ 值约为 0.1 时已被发现能产生最佳结果，这也是 Ansys Fluent 中的默认值。

4.16.2.2 动态 Smagorinsky-Lilly 模型

Germano 等人 [199]（第 1068 页）和随后的 Lilly [376]（第 1079 页）构想了一种程序，其中 Smagorinsky 模型常数 $C_s$ 是根据由解析尺度运动提供的信息动态计算的。因此，动态程序消除了用户预先指定模型常数 $C_s$ 的需要。

动态程序的概念是向运动方程应用第二个滤波器（称为测试滤波器）。新的滤波器宽度 $\hat{\Delta }$ 是网格滤波器宽度 $\Delta$ 的两倍。两种滤波器都产生一个解析的流动场。两个解析场之间的差异是介于网格滤波器和测试滤波器之间的小尺度的贡献。与这些尺度相关的信息用于计算模型常数。在 Ansys Fluent 中，如下面所述，考虑了模型的可变密度公式。

在测试滤波后的场级，SGS 应力张量可以表示为： $$T_{ij}=\widehat{\rho u_i{u}_j}-\left(\widehat{\rho u_i}\widehat{\rho u_j}/\hat{\rho }\right)\text{\hspace{1em}(4.309)}$$ $T_{ij}$ 和 ${\tau }_{ij}$ 均采用 Smagorinsky-Lilly 模型进行建模，假定尺度相似性： $${\tau }_{ij}=-2C\bar{\rho }{\Delta }^2\tilde{S}|\left({\tilde{S}}_{ij}-\frac{1}{3}{\tilde{S}}_{kk}{\delta }_{ij}\right)\text{\hspace{1em}(4.310)}$$ $$T_{ij}=-2C\hat{\rho }{\hat{\Delta }}^2\left|\hat{\tilde{S}}\right|\left({\hat{\tilde{S}}}_{ij}-\frac{1}{3}{\hat{\tilde{S}}}_{kk}{\delta }_{ij}\right)\text{\hspace{1em}(4.311)}$$ 在公式4.310（第122页）和公式4.311（第122页）中，系数C被假定为相同且与过滤过程无关（注意根据公式4.307（第121页），$C=C_s^2$）。网格过滤的亚格子（SGS）和测试过滤的亚格子通过Germano恒等式[199]（第1068页）相关联，如下所示： $$L_{ij}=T_{ij}-\widehat{{\tau }_{ij}}=\bar{\rho }\widehat{{\tilde{u}}_i}{\tilde{u}}_j-\frac{1}{\hat{\rho }}\left(\bar{\rho }{\hat{\tilde{u}}}_i\bar{\rho }{\hat{\tilde{u}}}_j\right)\text{\hspace{1em}(4.312)}$$ 其中，$L_{ij}$ 可从已解析的大涡场中计算得出。将网格滤波的Smagorinsky-Lilly模型及公式4.311（第122页）代入公式4.312（第122页），可推导出以下表达式，以求解由Lilly（1992）通过最小二乘法分析得到的收缩系数$\mathrm{C}$。 $$C=\frac{\left(L_{ij}-L_{kk}{\delta }_{ij}/3\right)M_{ij}}{M_{ij}{M}_{ij}}\text{\hspace{1em}(4.313)}$$ 以下文本的中文翻译：

[请提供需要翻译的文本内容，以便进行准确翻译。] $$M_{ij}=-2\left({\hat{\Delta }}^2\hat{\rho }\left|\hat{\tilde{S}}\right|{\hat{\tilde{S}}}_{ij}-{\Delta }^2\bar{\rho }\left|\hat{\tilde{S}}\right|{\tilde{S}}_{ij}\right)\text{\hspace{1em}(4.314)}$$ 在Ansys Fluent中，关于该模型的详细实现及其验证的更多信息，请参见[307]（第1075页）。

使用动态Smagorinsky-Lilly模型得到的$C_s=\sqrt{C}$在时间和空间上变化范围相当广泛。为了避免数值不稳定，方程4.313（第122页）中的分子和分母都采用测试滤波器进行局部平均（或滤波）处理。在Ansys Fluent中，$C_s$默认情况下还会被限制在0和0.23之间。

4.16.2.3 壁面自适应局部涡粘性（WALE）模型

在WALE模型[478]（第1084页）中，涡粘性是通过... $${\mu }_t=\rho L_s^2\frac{{\left(S_{ij}^d{S}_{ij}^d\right)}^{3/2}}{{\left({\bar{S}}_{ij}{\bar{S}}_{ij}\right)}^{5/2}+{\left(S_{ij}^d{S}_{ij}^d\right)}^{5/4}}\text{\hspace{1em}(4.315)}$$ 在WALE模型中，$L_s$ 和 $S_{ij}^d$ 分别定义为 $$L_s=\min \left(\kappa d,C_w{V}^{1/3}\right)\text{\hspace{1em}(4.316)}$$ $$S_{ij}^d=\frac{1}{2}\left({\bar{g}}_{ij}^2+{\bar{g}}_{ji}^2\right)-\frac{1}{3}{\delta }_{ij}{\bar{g}}_{kk}^2,{\bar{g}}_{ij}=\frac{\partial \overline{u_i}}{\partial x_j}\text{\hspace{1em}(4.317)}$$ 其中，$\kappa$ =0.41 是冯·卡门常数。WALE 常数 $C_w$ 的发表值为 0.5；然而，在涉及原始模型开发者的欧盟研究项目中进行的密集验证表明，在 Ansys Fluent 中使用 $C_w=0.325$ 时，结果始终更优，因此该值被用作默认设置。其余符号与 Smagorinsky-Lilly 模型相同。利用这一空间算子，WALE 模型旨在为壁面有界流动返回正确的壁面渐近 $\left(y^3\right)$ 行为。

WALE 模型的另一个优点是，它为层流剪切流动返回零湍流粘度。这允许在域中正确处理层流区域。相比之下，Smagorinsky-Lilly 模型产生非零湍流粘度。因此，与 Smagorinsky-Lilly 模型相比，WALE 模型更可取。

4.16.2.4 代数壁面模型化的大涡模拟模型（WMLES）

尽管在大气科学界广泛使用，大涡模拟（LES）在工业模拟中的影响却非常有限。原因在于壁边界层对分辨率的要求过高。在靠近壁面的区域，湍流谱中最大尺度尽管在几何上非常小，却需要非常精细的网格和较小的时间步长。此外，与雷诺平均模拟（RANS）不同，网格不仅需要在壁面法线方向上细化，还必须在壁面平行平面上解析湍流。这仅能在极低雷诺数和非常小的几何尺度上实现（LES域的范围不能比壁面平行方向上的边界层厚度大太多，通常不超过10-100倍）。因此，LES仅推荐用于那些壁边界层不相关且无需解析的流动，或者由于雷诺数较低而边界层为层流的流动。

然而，这类流动非常少，需要采用其他方法。克服LES雷诺数缩放限制的一个有前景的方法是代数壁模型LES（WMLES）方法[592]（第1091页）。在WMLES中，模型的RANS部分仅在内对数层内部激活，而边界层外部则由改进的LES公式覆盖。由于边界层的内部部分负责LES模型的雷诺数依赖性，WMLES方法可以在相同的网格分辨率下应用于通道流动模拟中不断增加的雷诺数。 需要注意的是，对于壁面边界层，雷诺数缩放并未完全避免，因为随着雷诺数的增加，边界层厚度相对于物体尺寸会减小。假设每个“边界层体积”有一定数量的网格节点，整体网格间距将减小，且随着雷诺数的增加，整体单元数量也会增加。

另一个有趣的选择，也可能是 WMLES 选项的最佳应用，是将其与 Ansys Fluent 中的嵌入式 LES（ELES）实现相结合。ELES 将 LES 区域限制在域的小区域，并用 RANS 覆盖不太关键的区域。WMLES 将此功能扩展到 LES 域中的高雷诺数。要应用此选项，请参阅用户指南中的“设置大涡模拟模型”和“设置嵌入式大涡模拟（ELES）模型”。

4.16.2.4.1 代数 WMLES 模型公式

原始的代数 WMLES 公式由 Shur 等人提出 [592]（第 1091 页）。它结合了混合长度模型、改进的 Smagorinsky 模型 [603]（第 1092 页）以及 Piomelli 的壁面阻尼函数 [520]（第 1087 页）。

在 Shur 等人的模型 [592]（第 1091 页）中，涡流粘度是通过使用混合长度尺度计算的： $$v_t=\min \left[{\left(\kappa d_w\right)}^2,{\left(C_{\text{Smag }}\Delta \right)}^2\right]\cdot S\cdot \left\{1-\exp \left[-{\left(y^{+}/25\right)}^3\right]\right\}\text{\hspace{1em}(4.318)}$$ 其中，$d_w$ 表示壁面距离，$S$ 是应变率，$\kappa =0.4187$ 和 $C_{S_{\text{mag }}}=0.2$ 为常数，而 $y^{+}$ 则是壁面法向的内尺度。大涡模拟（LES）模型基于修正的网格尺度，以考虑壁面模型化流动中的网格各向异性。 $$\Delta =\min \left(\max \left(C_w\cdot d_w;C_w\cdot h_{\max },h_{wn}\right);h_{\max }\right)\text{\hspace{1em}(4.319)}$$ 在这里，$h_{\max }$ 表示直角六面体网格单元的最大边长（对于其他单元类型和/或条件，会使用这一概念的扩展）。$h_{wn}$ 是壁面法向网格间距，而 $C_w=0.15$ 是一个常数。

上述模型已针对 Ansys Fluent 进行了优化，但仍保留了原始模型的精神。

4.16.2.4.1.1 雷诺数缩放

WMLES 公式的主要优势在于改进了雷诺数的缩放。对于壁面解析的 LES 的经典分辨率要求是 $${\Delta }_x^{+}=40,Ny=30,{\Delta }_z^{+}=20\text{\hspace{1em}(4.320)}$$ 哪里 $${\Delta }_x^{+}=\frac{u_{\tau }\Delta x}{v},{\Delta }_z^{+}=\frac{u_{\tau }\Delta z}{v}\text{\hspace{1em}(4.321)}$$ 其中，$Ny$表示跨过边界层$h$（或半通道高度$h$）的网格数，$\nu$为运动粘度。壁面摩擦速度定义为 $$u_{\tau }=\sqrt{\frac{{\tau }_{\mathrm{w}}}{\rho }}\text{\hspace{1em}(4.322)}$$ 其中，${\tau }_w$ 表示壁面剪切应力，$\rho$ 表示密度。

WMLES 的分辨率要求为 $${\Delta }_x=\frac{h}{10},Ny=30-40,{\Delta }_z=\frac{h}{20}\text{\hspace{1em}(4.323)}$$ 再次以 $\mathrm{h}=\frac{\mathrm{H}}{2}$ 计算（其中 $\mathrm{H}$ 为通道高度），或 $\mathrm{h}=\delta$（其中 $\delta$ 为边界层厚度）。

考虑一个在展向和流向方向上周期性的通道，其几何尺寸为： $$Lx=8h,Ly=2h,Lz=3h\text{\hspace{1em}(4.324)}$$ 您获得了以下通道内总细胞数（$({\mathrm{N}}_{\mathrm{T}}$ 通道内总细胞数），适用于壁面解析大涡模拟（LES）和WMLES：

• 壁面解析大涡模拟（LES）

表4.1：壁面解析网格尺寸随雷诺数变化

• WMLES：

表4.2：WMLES网格尺寸随雷诺数变化

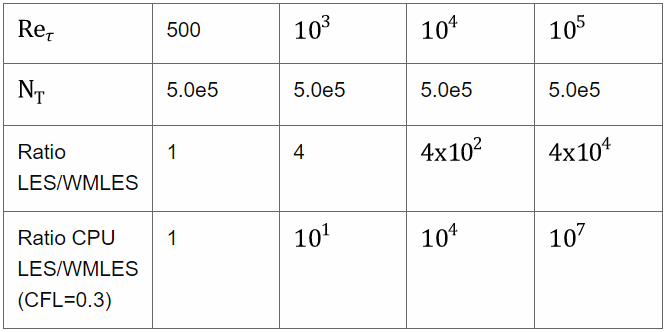
雷诺数基于摩擦速度计算。 $${\mathrm{Re}}_{\tau }=\sqrt{\frac{{\mathrm{u}}_{\tau }\mathrm{h}}{\nu }}\text{\hspace{1em}(4.325)}$$ 从上述表格中可以看出，壁面解析大涡模拟（Wall-Resolved LES）的二次雷诺数依赖性已被WMLES避免，并且CPU计算量大幅减少。

然而，仍然重要的是要记住，WMLES比雷诺平均模拟（RANS）在计算上更为昂贵。考虑一个壁面边界层流动，使用WMLES时，必须覆盖每个边界层体积$\left(\delta \times \delta \times \delta \right)$，在流向、法向和展向方向上分别使用$10\times \left(30-40\right)\times 20=6000-8000$个网格单元。而RANS可以估计为$1\times \left(30-40\right)\times 1=30-40$个网格单元。此外，RANS可以计算稳态结果，而WMLES需要进行CFL数约为$\sim 0.3$的不稳定模拟。

4.16.2.4.2 代数WMLES S-Omega模型公式

WMLES方法的一个缺陷是，在使用改进的Smagorinsky模型在LES区域时，模型没有提供对于恒定剪切流动的零涡粘性。因此，WMLES模型不允许计算过渡效应，并且在分离剪切层（如从后台阶）中可能产生过大的涡粘性。

增强WMLES公式（如公式4.318，第124页所示）的一种方法是使用差值abs $\left(S-\Omega \right)$代替$S$来计算模型的LES部分，其中$S$是应变率，$\Omega$是涡量大小。这种增强被称为WMLES $S$ - $\Omega$公式。

4.16.2.5 动态动能亚格子尺度模型

先前讨论的原始且动态的Smagorinsky-Lilly模型，本质上是一种代数模型，其中亚格子尺度应力是利用已解析的速度尺度进行参数化的。其基本假设是网格过滤尺度传递的能量与小尺度亚格子动能耗散之间的局部平衡。通过考虑亚格子尺度湍流动能的输运，可以更好地对亚格子尺度湍流进行建模。

Ansys Fluent中的动态亚格子尺度动能模型再现了Kim和Menon[310]（第1075页）提出的模型。

亚格子尺度动能被定义为 $$k_{sgs}=\frac{1}{2}\left(\overline{u_k^2}-{\bar{u}}_k^2\right)\text{\hspace{1em}(4.326)}$$ 这是通过收缩方程4.11（第43页）中的亚网格尺度应力得到的。

亚网格尺度涡粘性，${\mu }_{t^{\prime }}$，是利用$k_{sgs}$计算得出的。 $${\mu }_t=C_k\rho k_{sgs}^{1/2}{\Delta }_f\text{\hspace{1em}(4.327)}$$ 其中，${\Delta }_f$ 是从 ${\Delta }_f\equiv V^{1/3}$ 计算得到的滤波器尺寸。

于是，亚格子尺度应力可以表示为 $${\tau }_{ij}-\frac{2}{3}\rho k_{sgs}{\delta }_{ij}=-2C_k\rho k_{sgs}^{1/2}{\Delta }_f{\bar{S}}_{ij}\text{\hspace{1em}(4.328)}$$ 通过求解其输运方程，得到$k_{sgs}$。 $$\rho \frac{\partial {\bar{k}}_{sgs}}{\partial t}+\rho \frac{\partial {\bar{u}}_j{\bar{k}}_{sgs}}{\partial x_j}=-{\tau }_{ij}\frac{\partial {\bar{u}}_i}{\partial x_j}-C_{\epsilon }\rho \frac{k_{sgs}^{3/2}}{{\Delta }_f}+\frac{\partial }{\partial x_j}\left(\frac{{\mu }_t}{{\sigma }_k}\frac{\partial k_{sgs}}{\partial x_j}\right)\text{\hspace{1em}(4.329)}$$ 在上面的方程中，模型常数 $C_k$ 和 $C_{\epsilon }$ 是动态确定的 [310]（第1075页）。${\sigma }_k$ 被硬编码为 1.0。该模型在 Ansys Fluent 中的实现细节及其验证由 Kim [307]（第1075页）提供。

4.16.3 尺度解析模拟的入口边界条件

本节描述了 Ansys Fluent 中可用于模拟速度入口边界或压力入口边界处速度波动的算法。

如果在速度指定入口边界使用“无扰动”选项，则忽略流动的随机成分。在这种情况下，各个瞬时速度分量简单地设置为其平均速度的对应值。此选项仅适用于流入边界的湍流水平可以忽略不计或对整体解的准确性不占主导地位的情况。

重要提示：以下列出的方法适用于速度入口和压力入口边界条件。对于速度入口，波动加在指定的平均速度上。对于压力入口，动量方程中采用虚拟体积力来将重建的湍流波动添加到速度场中。这些虚拟体积力仅在靠近入口的第一层网格单元中考虑。

这些方法适用于 SAS、DES、SDES、SBES 和 LES 模型。域内是否能维持非定常性取决于流动和网格间距，尤其是在使用 SAS 或 DDES 模型进行有壁面限制的流动时。 这些方法需要现实的入口条件，例如提供$\mathrm{U}$、$\mathrm{k}$和$\epsilon$（或$\omega$）的剖面，这些可以从单独的RANS模拟中获得。入口处不现实的（“平坦”）湍流剖面会在入口处产生不现实的湍流涡旋。需要注意应用于入口速度和湍流量的转换操作的顺序，这在“从湍流强度估计湍流动能”中有解释。这个转换顺序在基于指定湍流强度计算波动幅度时非常重要。它还可以影响生成的合成湍流的其他属性，例如合成湍流生成器的全局时间尺度$\tau$，参见公式4.337（第129页）。这个时间尺度取决于入口速度，入口速度可能首先根据“常规任务页面”中选择的“速度公式”进行转换。

4.16.3.1 涡旋方法

为了生成时间依赖的入口条件，考虑了一种随机的二维涡旋方法。通过这种方法，在指定的平均速度剖面上添加了一个波动的涡量场（即在垂直于流动方向的平面上是二维的）来引入扰动。涡旋方法是基于涡量的二维演化方程的拉格朗日形式和比奥-萨伐尔定律。使用粒子离散化来求解这个方程。这些粒子，或称为“涡旋点”，随机对流并携带涡量场的信息。如果$N$是涡旋点的数量，$A$是入口截面的面积，那么给定粒子$i$携带的涡量由环流${\Gamma }_i$和一个假定的空间分布$\eta$表示： $${\Gamma }_i\left(x,y\right)=4\sqrt{\frac{\pi Ak\left(x,y\right)}{3N\left[2\ln \left(3\right)-3\ln \left(2\right)\right]}}\text{\hspace{1em}(4.330)}$$ $$\eta \left(\overrightarrow{x}\right)=\frac{1}{2\pi {\sigma }^2}\left(2e^{-{|x|}^2/2{\sigma }^2}-1\right)2e^{-{|x|}^2/2{\sigma }^2}\text{\hspace{1em}(4.331)}$$ 其中，$k$ 表示湍流动能。参数 $\sigma$ 用于控制涡旋粒子的大小。由此得到的关于速度场的离散化表达式为 $$\overrightarrow{u}\left(\overrightarrow{x}\right)=\frac{1}{2\pi }\sum _{i=1}^N{\Gamma }_i\frac{\left(\left({\overrightarrow{x}}_i-\overrightarrow{x}\right)\times \overrightarrow{z}\right)\left(1-e^{{|\overrightarrow{x}-\overrightarrow{x}|}^2/2{\sigma }^2}\right)}{{\left|\overrightarrow{x}-{\overrightarrow{x}}_i^{\prime }\right|}^2}\text{\hspace{1em}(4.332)}$$ 其中，$\overrightarrow{z}$ 表示流向上的单位向量。最初 [588]（第1091页），涡旋的大小通过一个特定的 $\sigma$ 值固定。为了使涡旋方法普遍适用，通过湍流混合长度假设来指定局部涡旋大小。根据入口处已知的平均湍流动能和平均耗散率分布，$\sigma$ 按照以下公式计算： $$\sigma =\frac{c{k}^{3/2}}{2\epsilon }\text{\hspace{1em}(4.333)}$$ 其中 $c=0.16$。为确保涡旋始终属于可解析尺度，方程4.333（第128页）中 $\sigma$ 的最小值受限于当地网格尺寸。每个涡旋的环流符号每隔一个特征时间尺度 $\tau$ 随机改变一次。在涡旋方法的一般实现中，这一时间尺度表示一个二维涡旋在边界法线方向上被整体速度输送，沿着 $n$ 倍其平均二维特征尺寸 $\left({\sigma }_m\right)$ 所需的时间，其中 $n$ 通过数值测试固定为100。涡旋方法仅考虑垂直于流线方向的平面内的速度波动。

然而，在Ansys Fluent中，对于流线方向速度波动采用了一种简化的线性运动学模型（LKM）[414]（第1081页）。该模型源自一个线性模型，模拟二维涡旋对流线方向平均速度场的影响。如果将平均流线方向速度 $U$ 视为被动标量，由平面波动速度场 $v^{\prime }$ 输送 $U$ 产生的波动 $u^{\prime }$ 则通过该模型进行模拟。 $$u^{\prime }=-{\overrightarrow{v}}^{\prime }\cdot \overrightarrow{g}\text{\hspace{1em}(4.334)}$$ 其中，$\overrightarrow{g}$ 是与平均速度梯度 $\overrightarrow{\nabla U}$ 对齐的单位向量。当这个平均速度梯度等于零时，可以考虑一个随机扰动来代替。

由于速度分量中的波动均匀分布，因此在域的入口处只能满足规定的动能分布。在下游更远的地方，正确的波动分布得以恢复 [414]（第 1081 页）。然而，如果入口处法向波动的分布已知或可以规定，则可以对合成流场应用重缩放技术，以满足入口处给出的法向统计波动 $<uu>,<vv>$ 和 $<ww>$。

通过重缩放程序，速度波动可以表示为： $$u_i^{\prime \ast }=u_i^{\prime }\frac{\sqrt{<u_i{u}_i>}}{\sqrt{2/3k}}\text{\hspace{1em}(4.335)}$$ 这同样改善了入口下游湍流流场的表示。此重缩放过程仅在将雷诺应力分量指定为雷诺应力指定方法时使用，而不是默认选项K或湍流强度。

注意：

涡流方法生成的速度波动不强制质量守恒。这可能导致解决声学问题时出现意外的压力波动和人为干扰或噪声。为了解决这个问题，您可以通过在入口对话框中选择“满足质量守恒？”来为涡流方法启用质量守恒。

重要提示：由于涡流方法理论基于对沿流向方向垂直的速度场的修改，因此您必须创建一个与流向速度方向垂直（或尽可能接近垂直）的入口平面。如果入口对流速度与${\mathrm{k}}^{0.5}$相当或更低，可能会出现问题，因为这可能导致局部流出。因此，对于$\mathrm{Tu}\sim 1$或更小的情况，应谨慎应用。

涡旋方法在整个选定的边界上覆盖了涡旋，即使在入流湍流水平较低的区域（自由流）也是如此。出于效率考虑，建议您将涡旋方法的域限制在希望生成非定常湍流的区域。例如，假设一个薄混合层通过一个更大的入口区域进入。此时，建议将入口边界分为三部分：混合层下方的部分，具有恒定的入口速度；混合层进入域的部分，使用涡旋方法；以及混合层上方的第三部分，再次具有恒定速度。这样，涡旋就集中在感兴趣的域中。否则，需要生成大量的涡旋以确保在薄混合层区域中有足够数量的涡旋。

4.16.3.2 谱合成器

谱合成器提供了一种生成波动速度分量的替代方法。它基于最初由Kraichnan [322]（第1075页）提出的随机流动生成技术，并由Smirnov等人 [605]（第1092页）进行了修改。在这种方法中，波动速度分量是通过从傅里叶谐波的总和中合成一个无散度的速度矢量场来计算的。在Ansys Fluent中，默认的傅里叶谐波数量设置为250。

4.16.3.3 合成湍流生成器

为了生成用于尺度解析湍流模拟的时间依赖入口条件，使用了基于傅里叶的合成湍流生成器。

与其他现有方法相比，这种方法在计算时间上成本较低，同时能够实现高质量的湍流波动。 在进口边界条件的某点 $\mathbf{r}=\{x,y,z\}$ 处，速度矢量被指定为平均速度矢量与合成速度脉动矢量的总和： $$\mathbf{U}\left(\mathbf{r},t\right)={\mathbf{U}}_{\text{Inlet, mean }}\left(\mathbf{r}\right)+{\mathbf{u}}^{\prime }\left(\mathbf{r},t\right)\text{\hspace{1em}(4.336)}$$ 速度波动场 ${\mathbf{u}}_i^{\prime }\left(\mathbf{r},t\right)$ 被定义为加权时空傅里叶模态的叠加，其尺度调整使得入口边界处相应的动能与规定的RANS动能 $K_t$ 相等。 $${\mathbf{u}}^{\prime }\left(\mathbf{r},t\right)=2K_t\sum _{n=1}^N\sqrt{q^n}\left[{\sigma }^n\cos \left(k^n{\mathbf{d}}^n\cdot \mathbf{r}+{\varphi }^n+s^n\frac{t}{\tau }\right)\right]\text{\hspace{1em}(4.337)}$$ 其中：

$N$ 表示模式的数量。

$q^n$ 是模式 $n$ 的归一化振幅，由局部能量谱定义。

$k^n$ 是模式 $n$ 的波数矢量的振幅。

${\mathbf{d}}^n$ 是一个均匀分布在球面上的随机单位方向矢量。

${\sigma }^n$ 是一个垂直于 ${\mathbf{d}}^n$ 的单位矢量（即 ${\sigma }^n\cdot {\mathbf{d}}^n=0$），并且在垂直于 ${\mathbf{d}}^n$ 的平面内，其方向由一个均匀分布在区间 $\left(0,2\pi \right)$ 内的随机数定义。

${\phi }^n$ 是模式 $n$ 的相位，也是一个均匀分布在区间 $\left(0,2\pi \right)$ 内的随机数。

$s^n$ 是模式 $n$ 的无量纲频率，具有高斯分布，均值和标准差均为 $2\pi$。

$\tau$ 是全局时间尺度。它基于特征长度和速度尺度，这些尺度定义为入口区域最大 RANS 湍流长度尺度和速度。

重要提示：如果仅有一小部分进口面区域产生合成湍流，那么使用整个进口区域来确定特征尺度可能会导致不正确的结果。例如，如果自由流中的RANS湍流长度尺度任意高，那么在湍流边界层中可能会生成不切实际的长湍流结构。在这种情况下，有必要将全局尺度的计算区域限制在进口的相关部分，其效果如下图所示。为了限制搜索区域，可以指定尺度搜索限制器：湍流动能、湍流粘度比或壁面距离阈值。然后，仅使用进口面区域中相应进口湍流参数高于指定阈值（湍流动能、湍流粘度比）或简单地距离壁面小于指定壁面距离阈值的部分来计算速度和长度尺度。限制器可以在速度或压力进口对话框中指定，或者使用控制台命令设置边界条件（/define/boundary-conditions/set）。

图4.11：在自由流中湍流长度尺度任意高的情况下，合成湍流生成器在边界层中生成的湍流结构：

未设置尺度搜索限制器选项（左）和设置指定湍流动能阈值2%（右） 基于面的（默认）合成湍流生成器会产生虚假的压力波动，使其不适用于气动声学模拟。体积版本仅适用于基于omega的SBES模型，可以通过选择“体积力”在速度或压力入口处启用。它通过在从边界开始的三个维度强迫区域内引入湍流波动的体积源到动量方程中，避免了产生不希望的噪声。噪声的减少使得合成湍流生成器可以应用于声学任务。

在体积强迫区域内，SBES模型以LES模式工作，这可能会在存在边界层的情况下（例如，如果体积合成湍流生成应用于与壁面相连的边界条件）导致不准确性。可以通过可视化SBES混合函数来检查SBES模型的行为。

您可以选择指定一个基于湍流长度尺度的自动强迫区域厚度，或者通过指定值直接设置强迫区域厚度。

注意：与涡旋方法不同，合成湍流生成器的质量守恒默认启用，无法禁用。

更多详情，请参见[594]（第1091页）。

4.16.3.3.1 限制

在Ansys Fluent的当前版本中，体积力通用实现是一项具有挑战性的任务，因为它需要正确识别施力区域。在该方法中，所有位于考虑的入口区域相邻单元区内的单元都被标记为施力对象，这些单元位于从入口区域开始计算的施力区域厚度范围内。沿着垂直于入口方向，计算每个单元中心与入口区域中心之间的距离。在平行于入口方向上，标记的单元层可能比入口区域更大。然而，施力强度会根据建模的湍流动能进行缩放，该能量来源于其输运方程。因此，在来自相邻入口区域的湍流流场之外，施力强度为零。但是，如果标记的单元层穿越了求解场中的其他湍流部分，这将在那些部分也产生施力，这通常是不希望的。这种情况如图4.12所示：在复杂流动模拟中分割单元区以避免体积力的不良副作用（第132页）。

图4.12：在复杂流动模拟中分割单元区以避免体积力的不良副作用

在这种情况下，将大型单元区分割成较小的部分有助于限制标记的单元层，并避免在不希望的位置产生虚假的施力。