应力混合涡模拟(SBES)是一种混合RANS-LES湍流模型,它使用与SDES公式相同的屏蔽函数(参见屏蔽分离涡模拟(SDES)(第114页)),并增加了直接从底层RANS模型切换(混合)到任何现有代数LES模型的能力(同样基于屏蔽函数)。这一功能为SBES模型命名。
注意:尚未对SBES与转换模型(Transition SST、间歇性转换模型或代数转换模型)的组合进行特殊校准。
4.15.1 应力混合
在SDES框架内开发的屏蔽函数可以扩展,以实现RANS和LES公式之间在应力水平上的混合。一般来说,这会影响湍流应力张量,如下所示: 其中, 代表 RANS 模型部分,而 则代表 LES 模型部分,它们共同构成了模化应力张量。当这两种模型均基于涡粘性概念时,公式可简化为: 这种表述之所以可行,完全得益于屏蔽函数 的强大屏蔽性能(如前一节所述)。
SBES 模型的主要优势在于,它允许你在流动的 LES 部分使用特定的 LES 模型,而非依赖于类似 DES 模型的 LES 能力。此外,你还可以利用它来直观显示 RANS 和 LES 模型的应用区域,以便检查设置的一致性。最后,SBES 模型使得在分离剪切层中从 RANS 快速“转换”到 LES 成为可能。
总结来说,SBES 模型使你能够:
- 通用地结合 RANS 和 LES 模型公式
- 基于 函数清晰区分 RANS 和 LES 区域
- 由于 LES 模型施加的低应力水平,在分离剪切层中实现从 RANS 到 LES 的快速“转换”
4.15.2 SDES 和 SBES 示例
以下示例展示了 SDES 和 SBES 模型在从喷嘴喷射出的射流中的应用。图 4.8:亚音速射流流动的计算域和网格(第 118 页)展示了其几何形状和网格。圆形射流流动已由
Viswanathan [675](第 1096 页)在马赫数 和基于射流直径 以及喷嘴出口处的体积速度 的雷诺数 下进行了实验研究。计算网格由 个六面体单元组成。
图 4.8:亚音速射流流动的计算域和网格
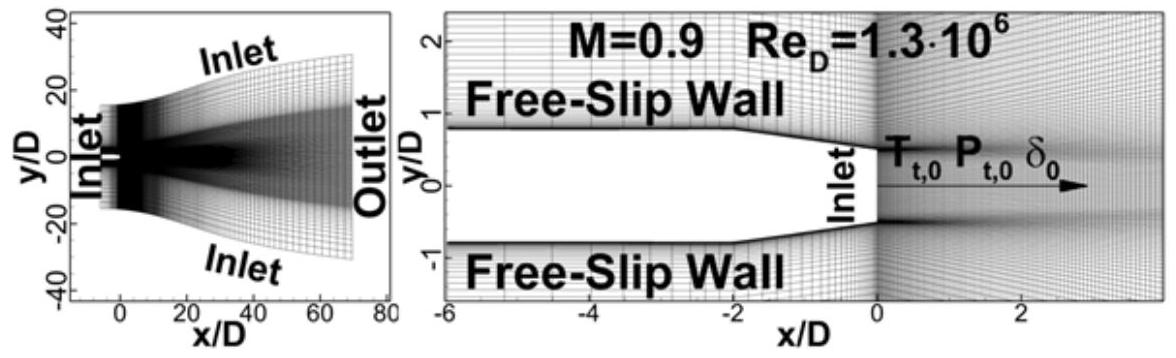 图4.9:Q准则等值面着色速度大小(第119页)展示了不同模型下湍流结构的形成。混合RANS-LES模型的主要目标是以尽可能快的速度从稳态RANS模式“转换”到尺度解析的三维LES模式。
图4.9:Q准则等值面着色速度大小(第119页)展示了不同模型下湍流结构的形成。混合RANS-LES模型的主要目标是以尽可能快的速度从稳态RANS模式“转换”到尺度解析的三维LES模式。
从图4.9:Q准则等值面着色速度大小(第119页)可以看出,SDES和SBES提供了从二维RANS到三维LES结构的相对快速的转换。最快的转换由SBES公式实现,其次是SDES。DDES产生了几乎轴对称的结构,这些结构在喷嘴处明显更远距离内占主导地位。
图4.9:Q准则等值面着色速度大小

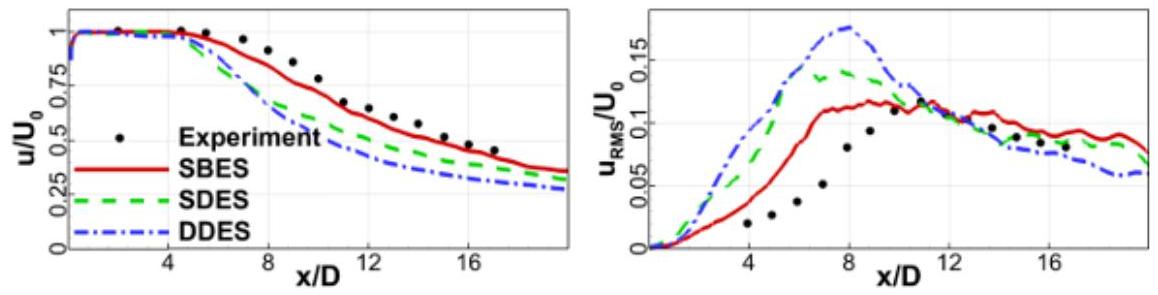
图4.10:射流中心线上的平均(左)和RMS(右)速度分布(第119页)展示了与实验数据的比较。左图显示了沿射流中心线的平均轴向速度,右图显示了相应的顺流RMS波动。从两者的比较中可以清楚地看出,随着模型快速切换到LES模式的能力增强,与数据的吻合度有所提高。
图4.10:射流中心线上的平均(左)和RMS(右)速度分布