屏蔽分离涡模拟（SDES）是一种混合RANS-LES湍流模型家族。从DDES-SST模型开始（详见DES与BSL或SST k-ω模型的结合（第111页）），它提供了显著的改进：

• 一个屏蔽函数，保护RANS壁面边界层区域免受LES模型的影响
• 改进了网格长度尺度的定义，使得在分离剪切层中从RANS到LES的“过渡”更快

改进的屏蔽函数几乎完美地保护了边界层免受过早切换到LES模型的影响。否则，这种过早切换可能会导致模型在附着边界层中的RANS能力严重恶化[622]（第1093页）。

注意：尚未对SDES与Transition SST和Intermittency Transition模型的组合进行特殊校准。

请注意，在任何混合RANS-LES模型中激活自由流中的LES项都可能影响自由流湍流的衰减，进而影响过渡位置。

有关展示SDES模型效果的示例，请参见SDES和SBES示例（第118页）。

4.14.1 屏蔽函数

屏蔽分离涡模拟（SDES）屏蔽函数的发展起点是现有的延迟分离涡模拟（DDES）模型（详见分离涡模拟（DES）（第109页））。在DDES中，主要目标是模拟RANS模式下的附着和轻微分离边界层，然后在分离（脱离）剪切层中切换到LES模式。从给定的RANS模型开始，通过修改两方程模型中的$k$方程的汇项来实现DDES公式。在SST模型的$k$方程中，修改被重新表述如下： $${\epsilon }_{\mathrm{DDES}}=-{\beta }^{\ast }\rho k\omega F_{\mathrm{DDES}}\text{\hspace{1em}(4.288)}$$ 式中： $$F_{\mathrm{DDES}}=\left[\max \left(\frac{L_t}{C_{\mathrm{DES}}{\Delta }_{\max }}\left(1-f_{\mathrm{DDES}}\right),1\right)-1\right]\text{\hspace{1em}(4.289)}$$ 在上述方程中，$L_t$ 表示湍流长度尺度，${\Delta }_{\max }$ 是局部网格单元的最大边长，$f_{\text{DDES }}$ 是DDES屏蔽函数，而 $C_{\text{DES }}$ 是一个系数。当 $F_{\text{DDES }}$ 等于零时，RANS模型得以恢复。这种情况发生在满足以下一个或两个条件时： $$f_{\text{DDES }}=1\text{\hspace{1em}(4.290)}$$ 以及/或 $$\frac{L_t}{C_{\mathrm{DES}}{\Delta }_{\max }}<1\text{\hspace{1em}(4.291)}$$ 函数 $f_{\text{DDES }}$ 旨在保护附着边界层在切换到LES模式时不受影响。边界层受到影响的下限取决于网格间距与边界层厚度的比值（例如，$r={\Delta }_{\max }/\delta$）。在没有屏蔽（即 $f_{\mathrm{DDES}}=0$ 时）的情况下，该下限大约为 $r=1$，因此在 $r<1$ 时，边界层内的解会受到DES汇项的影响。根据分离涡模拟（DES）（第109页）中给出的屏蔽函数，$r$ 的下限降低到0.2-0.3，具体取决于压力梯度。违反这些限制会产生严重后果，因为RANS解将受到影响，而您可能并未察觉。DES/DDES方法最初是为飞机模拟开发的，其中边界层相对于飞机/机翼的尺寸通常较薄。在这些条件下（以及严谨的网格生成实践中），通常可以确保上述 $r$ 的限制。然而，对于一般的工业应用，由于雷诺数较低、对网格间距的控制较少以及组件间更复杂的相互作用，确保这些限制更为困难。

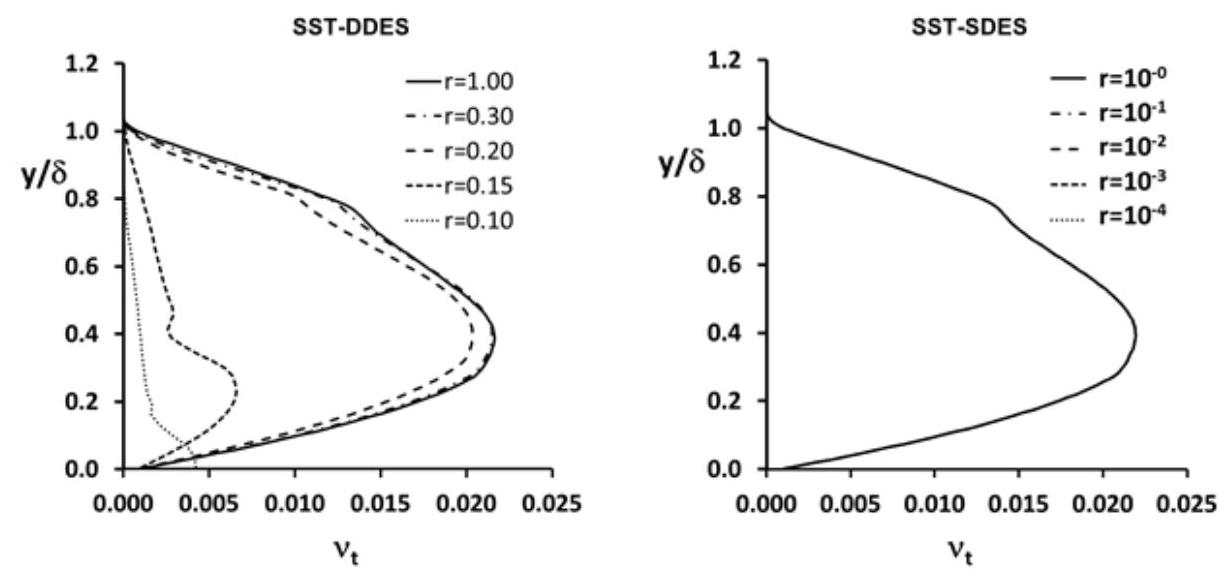
因此，SDES方法开发的首要目标是重新定义函数 $f_{\text{DDES }}$，以实现更可靠的屏蔽，即在附着边界层中进行比DDES更严格的网格细化时，仍能保持RANS边界层的能力。为此，开发了一种新的、未公开且为Ansys专有的屏蔽函数，称为 $f_{\text{SDES }}$，它比目前使用的 $f_{\text{DDES }}$ 函数提供了更安全的屏蔽。由此产生的汇项与DDES模型中的汇项相当： $${\epsilon }_{\mathrm{SDES}}=-{\beta }^{\ast }\rho k\omega F_{\mathrm{SDES}}\text{\hspace{1em}(4.292)}$$ 这里 $$F_{\mathrm{SDES}}=\left[\max \left(\frac{L_t}{C_{\mathrm{SDES}}{\Delta }_{\mathrm{SDES}}}\left(1-f_{\mathrm{SDES}}\right),1\right)-1\right]\text{\hspace{1em}(4.293)}$$ 图4.7：涡粘性剖面（第116页）展示了在网格细化下自相似零压力梯度边界层模拟中的涡粘性，其中$r={\Delta }_{\max }/\delta$（注意两种模型中细化比率$r$的不同范围）。SDES屏蔽（右侧）明显优于DDES屏蔽，即使在严重的网格细化下也能保持RANS边界层。

图4.7：涡粘性剖面

4.14.2 SDES的LES模式

SDES模型切换到LES模式后，额外的源项被激活，并将涡粘性降低到与传统LES模型相当的水平。所达到的涡粘性水平可以通过对基础RANS模型（在此情况下为SST模型）的源项施加平衡来估算。这意味着忽略$k$和$\omega$方程中的对流和扩散项，并使源项和汇项相等。结果为： $$v_t=={\left({\left(\frac{\beta }{\alpha }\right)}^{3/4}{C}_{\mathrm{LES}}\Delta \right)}^{2}S\text{\hspace{1em}(4.294)}$$ 其中，$S$ 表示应变率，$\alpha$ 和 $\beta$ 分别是 $\omega$ 方程中源项和汇项的常数。$C_{\mathrm{LES}}$ 代表不同模型中使用的常数 $C_{\mathrm{DES}}$ 和 $C_{\mathrm{SDES}}$，而 $\Delta$ 表示不同模型中使用的网格间距定义。显然，这种表述等同于经典的 Smagorinsky 模型（参见亚格子尺度模型，第 120 页）。${\left(\beta /\alpha \right)}^{3/4}{C}_{\mathrm{LES}}$ 的组合等同于 Smagorinsky 模型中的常数 $C_s$。使用 SST 模型中与 LES 区域相关的常数 $\left(\alpha =0.44,\beta =0.083,C_{\mathrm{DES}}=0.61\right)$，可以得到 DES / DDES 模型中相当于 $C_s=0.175$ 的值。这与推荐用于 Smagorinsky 模型进行衰减各向同性湍流 (DIT) 模拟的 $C_s=0.18$ 值接近。这并不令人意外，因为 DES / DDES 的 LES 部分是针对 DIT 进行校准的。然而，众所周知，Smagorinsky 模型需要针对 DIT 和剪切湍流使用不同的校准常数。对于剪切流，$C_s$ 的值更接近于 $C_s=0.11$。由于剪切流对于工程模拟更为重要，因此决定在 SDES 模型中使用 $C_{\mathrm{SDES}}=0.4$，以达到所需的等效 $C_s$ 常数值。 在DES/DDES模型中，LES长度尺度的定义为$\Delta ={\Delta }_{\max }$。这种定义存在问题，因为它可能导致分离剪切层中涡粘度过高，在这些区域网格纵横比通常较大（例如，从背风台阶分离的流动，其中展向网格间距远大于其他两个方向的网格间距）。这会导致从RANS模式到LES模式的“过渡”变得缓慢。为了避免这一问题，SDES模型采用了以下公式来定义LES长度尺度： $${\Delta }_{\mathrm{SDES}}=\max \left(\sqrt[3]{V},0.2{\Delta }_{\max }\right)\text{\hspace{1em}(4.295)}$$ 第一部分是基于单元体积$V$的经典长度尺度，第二部分确保了在高纵横比情况下的有效极限。与DES定义相比，这种表述在高纵横比网格中要小五倍。

需要注意的是，常数$C_{\mathrm{DES}}/C_{\mathrm{SDES}}$和网格定义都以平方形式进入等效Smagorinsky模型。对于高度拉伸的网格，如典型的分离剪切层，较低的${\mathcal{C}}_{\text{SDES }}$常数和较小的网格间距定义的组合效应，使得与DES/DDES相比，SDES的涡黏性水平降低了60倍。

还应注意的是，这两种修改同样可以应用于DES/DDES模型公式。然而，这样的改变会严重削弱DES/DDES公式的屏蔽特性，这些特性基于$C_{\mathrm{DES}}{\Delta }_{\max }$的组合。单独或组合降低这些值会损害这些模型的屏蔽特性。