4.11.1 概述

雷诺应力模型 (RSM) [203] (第 1068 页), [338] (第 1076 页), [339] (第 1076 页) 是 Ansys Fluent 提供的最复杂的 RANS 湍流模型类型。该模型放弃了各向同性涡粘性假设，通过求解雷诺应力的输运方程以及耗散率的方程来封闭雷诺平均 Navier-Stokes 方程。这意味着与三维流动相比，二维流动需要五个额外的输运方程，而三维流动则需要七个额外的输运方程。

由于 RSM 比单方程和双方程模型更严格地考虑了流线曲率、旋涡、旋转和应变率的快速变化等效应，因此它更有可能为复杂流动提供准确的预测。然而，RSM 预测的准确性仍然受到用于模拟雷诺应力精确输运方程中各种项的封闭假设的限制。压力-应变项和耗散率项的建模尤为具有挑战性，并且通常被认为是影响 RSM 预测准确性的关键因素。此外，即便是雷诺应力模型（RSM）也依赖于尺度方程（ $ε$ 或 $ω$ / BSL-），并继承了这些方程基础假设所导致的缺陷。Ansys Fluent提供了以下模型组合：

基于 $ε$ 的雷诺应力模型：
- 线性压力应变模型
- 二次压力应变模型
基于 $ω$ 的雷诺应力模型：
- 应力- $ω$ 模型
- 应力-BSL模型

Ansys Fluent中的默认雷诺应力模型基于 $ε$ 方程，并采用线性模型处理压力应变项。第二种基于 $ε$ 的模型允许使用二次模型来处理压力应变项。

基于 $ω$ 方程的两个雷诺应力模型均采用线性模型处理压力应变项，但在尺度方程方面有所不同：应力- $ω$ 模型基于 $ω$ 方程，而应力-BSL模型则从基准（BSL） $k$ - $ω$ 模型中求解尺度方程，从而消除了应力- $ω$ 模型中观察到的自由流敏感性。

雷诺应力模型（RSM）并不总能产生明显优于简单模型的结果，以证明额外的计算成本是合理的。然而，当关注的流动特征是由雷诺应力的各向异性引起时，使用RSM是必不可少的。例如，旋风流动、燃烧器中的高度旋流、旋转流动通道以及管道中应力诱导的二次流动等。

雷诺应力输运方程的确切形式可以通过对精确动量方程取矩来推导。这是一个过程，其中精确的波动动量方程与波动速度相乘并取平均，然后将乘积进行雷诺平均。平均而言，不幸的是，精确方程中的几个项是未知的，需要建模假设才能封闭方程。

4.11.2 雷诺应力输运方程

雷诺应力 $ρ \overline{u_{i}^{'} u_{j}^{'}}$ 的精确输运方程可以写成如下形式：

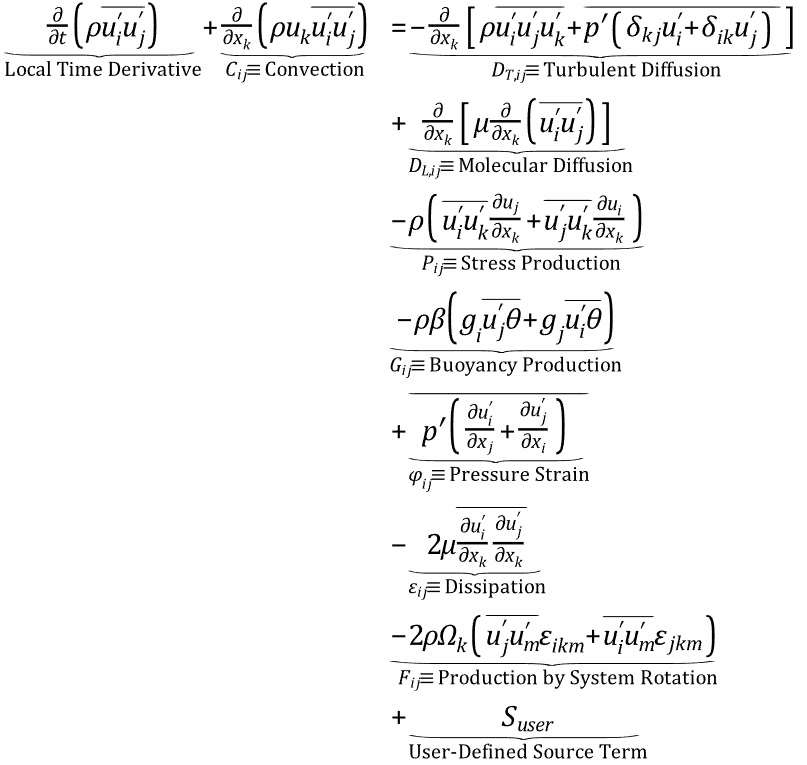
在这些精确方程的各项中， $C_{ij}, D_{L, ij}, P_{ij}$ 和 $F_{ij}$ 不需要任何建模。然而， $D_{T, ij}, G_{ij}, φ_{ij}$ 和 $ε_{ij}$ 需要建模以封闭方程。以下部分描述了封闭方程集所需的建模假设。

4.11.3 湍流扩散输运的建模

对于基于 $ε$ 的雷诺应力模型， $D_{T, ij}$ 可以通过Daly和Harlow [132]（第1064页）的广义梯度扩散模型来建模： $D_{T, ij} = C_{s} \frac{\partial}{\partial x _{k}} (ρ \frac{k u _{k}^{'} u _{ℓ}^{'}}{ε} \frac{\partial u _{i}^{'} u _{j}^{'}}{\partial x _{ℓ}}) (4.227)$ 然而，这一方程可能导致数值不稳定，因此Ansys Fluent对其进行了简化，采用了一个标量湍流扩散率，如下所示[371]（第1078页）： $D_{T, ij} = \frac{\partial}{\partial x _{k}} (\frac{μ _{t}}{σ _{k}} \frac{\partial u _{i}^{'} u _{j}^{'}}{\partial x _{k}}) (4.228)$ 湍流粘度 $μ_{t}$ 是根据公式 4.259（第 104 页）计算的，适用于基于 $ε$ 的 RSM。

Lien 和 Leschziner [371]（第 1078 页）通过将广义梯度扩散模型（公式 4.227，第 98 页）应用于平面均匀剪切流动的情况，推导出 $σ_{k} = 0.82$ 的值。请注意，这个 $σ_{k}$ 的值与标准和可实现的 $k$ - $ε$ 模型中的值不同，后者的 $σ_{k} = 1.0$ 。

对于基于 $ω$ 的雷诺应力模型，也使用公式 4.228（第 98 页）来模拟湍流扩散传输，湍流粘度则根据公式 4.74（第 62 页）计算。

应力-omega 模型将 $σ_{k}$ 设定为 2.0，而应力-BSL 模型则使用公式 4.107（第 66 页）中的混合函数 $F_{1}$ ，在内部区域（ $σ_{k, 1} = 2.0$ ）和外部区域（ $σ_{k, 2} = 1.0$ ）之间进行混合： $σ_{k} = F_{1} σ_{k, 1} + (1 - F_{1}) σ_{k, 2} (4.229)$

4.11.4 压力-应变项建模

Ansys Fluent 提供了基于 $ε$ 或 $ω$ / BSL 方程的以下雷诺应力模型：

基于 $ε$ 的雷诺应力模型：
- 线性压力-应变模型
- 二次压力-应变模型
基于 $ω$ 的雷诺应力模型：
- 应力-omega 模型
- 应力-BSL 模型

4.11.4.1 线性压力-应变模型

在 Ansys Fluent 中，默认情况下，方程 4.226（第 98 页）中的压力-应变项 $φ_{ij}$ 是根据 Gibson 和 Launder [203]（第 1068 页）、Fu 等人 [194]（第 1068 页）以及 Launder [337]（第 1076 页）、[338]（第 1076 页）的建议进行建模的。

对 $φ_{ij}$ 进行建模的经典方法采用以下分解： $φ_{ij} = φ_{ij, 1} + φ_{ij, 2} + φ_{ij, w} (4.230)$ 其中， $φ_{ij, 1}$ 是慢速压力应变项，也称为各向同性恢复项， $φ_{ij, 2}$ 被称为快速压力应变项，而 $φ_{ij, w}$ 是壁面反射项。

慢速压力应变项，即 $φ_{ij, 1^{'}}$ ，被建模为 $φ_{ij, 1} \equiv - C_{1} ρ \frac{ε}{k} [\overline{u_{i}^{'} u_{j}^{'}} - \frac{2}{3} δ_{ij} k] (4.231)$ 其中， $C_{1} = 1.8$ 。

快速压力-应变项， $φ_{ij, 2^{'}}$ ，被建模为 $φ_{ij, 2} \equiv - C_{2} [(P_{ij} + F_{ij} + 5/6 G_{ij} - C_{ij}) - \frac{2}{3} δ_{ij} (P + 5/ 6 G - C)] (4.232)$ 其中， $C_{2} = 0.60$ ， $P_{ij}$ 、 $F_{ij}$ 、 $G_{ij}$ 以及 $C_{ij}$ 的定义见公式 4.226（第 98 页）， $P = \frac{1}{2} P_{kk}$ ， $G = \frac{1}{2} G_{kk}$ ，以及 $C = \frac{1}{2} C_{kk}$ 。

壁面反射项 $φ_{ij, w^{'}}$ 负责在壁面附近重新分配法向应力。

它倾向于抑制垂直于壁面的法向应力，同时增强平行于壁面的应力。此项被建模为 $φ_{ij, w} \equiv C_{1 k}^{^{'}} \frac{ε}{k} [\overline{u_{k}^{^{'}} u_{m}^{^{'}}} n_{k} n_{m} δ_{ij} - \frac{3}{2} \overline{u_{i}^{^{'}} u_{k}^{^{'}}} n_{j} n_{k} - \frac{3}{2} \overline{u_{j}^{^{'}} u_{k}^{^{'}}} n_{i} n_{k}] \frac{C _{t} k ^{3/2}}{ε d} + C_{2}^{^{'}} [φ_{km, 2} n_{k} n_{m} δ_{ij} - \frac{3}{2} φ_{ik, 2} n_{j} n_{k} - \frac{3}{2} φ_{jk, 2} n_{i} n_{k}] \frac{C _{t} k ^{3/2}}{ε d} (4.233)$ 其中， $C_{1}^{'} = 0.5$ ， $C_{2}^{'} = 0.3$ ， $n_{k}$ 是壁面单位法向的 $x_{k}$ 分量， $d$ 是到壁面的法向距离，而 $C_{ℓ} = C_{μ}^{3/4} / κ$ ，其中 $C_{μ} = 0.09$ ， $κ$ 是 von Kármán 常数 $(= 0.4187)$ 。 $φ_{ij, w}$ 在雷诺应力模型中默认包含。

4.11.4.2 线性压力-应变模型的低雷诺数修正

当使用增强壁面处理描述的近壁流动应用雷诺应力模型（参见增强壁面处理的二层模型，第145页）时，必须对压力-应变模型进行修正。Ansys Fluent 中使用的修正根据 Launder 和 Shima [341]（第1077页）的建议，将 $C_{1}$ 、 $C_{2}$ 、 $C_{1}^{'}$ 和 $C_{2}^{'}$ 的值指定为雷诺应力不变量和湍流雷诺数的函数。 $C_{1} = 1 + 2.58 A A_{2}^{0.25} {1 - exp [- (0.0067 R e_{t})^{2}]} (4.234)$ $C_{2} = 0.75 A (4.235)$ $C_{1}^{'} = - \frac{2}{3} C_{1} + 1.67 (4.236)$ $C_{2}^{'} = max [\frac{\frac{2}{3} C _{2} - \frac{1}{6}}{C _{2}}, 0] (4.237)$ 定义了湍流雷诺数为 $R e_{t} = (ρ k^{2} / μ ε)$ 。扁平度参数 $A$ 和二阶、三阶张量不变量 $A_{2}$ 和 $A_{3}$ 定义如下： $A \equiv [1 - \frac{9}{8} (A_{2} - A_{3})] (4.238)$ $A_{2} \equiv a_{ik} a_{ki} (4.239)$ $A_{3} \equiv a_{ik} a_{kj} a_{ji} (4.240)$ $a_{ij}$ 是雷诺应力各向异性张量，定义为 $a_{ij} = - (\frac{- ρ u _{i}^{'} u _{j}^{'} + \frac{2}{3} ρ k δ _{ij}}{ρ k}) (4.241)$ 上述修改仅在粘性模型对话框中选择增强壁面处理时才会应用。

4.11.4.3 二次压力-应变模型

Ansys Fluent 提供了 Speziale、Sarkar 和 Gatski [625]（第 1093 页）提出的可选压力-应变模型。该模型在一系列基本剪切流动中，包括平面应变、旋转平面剪切和轴对称膨胀/收缩，已证明具有优越的性能。这种改进的准确性对更广泛的复杂工程流动，特别是那些具有流线曲率的流动，应该是有益的。二次压力-应变模型可以在粘性模型对话框中作为选项进行选择。

该模型表述如下： $φ_{ij} = - (C_{i} ρε + C_{1}^{*} P) b_{ij} + C_{z} ρε (b_{ik} b_{kj} - \frac{1}{3} b_{mn} b_{mn} δ_{ij}) + (C_{s} - C_{3}^{*} b_{ij} b_{ij}) ρ k S_{ij} + C_{4} ρ k (b_{ik} S_{jk} + b_{jk} S_{ik} - \frac{2}{3} b_{mn} S_{mn} δ_{ij}) + C_{5} ρ k (b_{ik} Ω_{jk} + b_{jk} Ω_{ik}) (4.242)$ 其中， $b_{ij}$ 是雷诺应力各向异性张量，定义为 $b_{ij} = - (\frac{- ρ u _{i}^{'} u _{j}^{'} + \frac{2}{3} ρ k δ _{ij}}{2 ρ k}) (4.243)$ 平均应变率 $S_{ij}$ 定义为 $S_{ij} = \frac{1}{2} (\frac{\partial u _{j}}{\partial x _{i}} + \frac{\partial u _{i}}{\partial x _{j}}) (4.244)$ 平均旋转率张量 $Ω_{ij}$ 定义为： $Ω_{ij} = \frac{1}{2} (\frac{\partial u _{i}}{\partial x _{j}} - \frac{\partial u _{j}}{\partial x _{i}}) (4.245)$ 常数是 $C_{1} = 3.4, C_{1}^{*} = 1.8, C_{2} = 4.2, C_{3} = 0.8, C_{3}^{*} = 1.3, C_{4} = 1.25, C_{5} = 0.4$ 二次压力-应变模型在湍流边界层的对数区域中不需要进行壁面反射效应的修正即可获得满意的解。然而，需要注意的是，当在黏性模型对话框中选择增强壁面处理时，二次压力-应变模型是不可用的。

4.11.4.4 应力-Omega模型

应力-Omega模型是一种基于Omega方程和LRR模型的应力输运模型[708]（第1098页）。该模型非常适合模拟流过曲面和旋流的情况。应力-Omega模型可以在黏性模型对话框中选择，并且不需要进行壁面反射处理。其闭合系数与 $k - ω$ 模型（模型常数（第65页））相同，但增加了额外的闭合系数 $C_{1}$ 和 $C_{2}$ ，如下所述。

应力-Omega模型因其对广泛湍流流动的优秀预测能力而与 $k - ω$ 模型相似。此外，低雷诺数修正和粗糙表面的表面边界条件与 $k - ω$ 模型类似。

公式4.230（第99页）可以为应力-Omega模型重新编写，以排除壁面反射： $φ_{ij} = φ_{ij, 1} + φ_{ij, 2} (4.246)$ 因此， $ϕ_{ij} = - C_{1} ρ β_{RSM}^{*} ω [\overline{u_{i}^{'} u_{j}^{'}} - 2 /_{3} δ_{ij} k] - \overset{α}{^}_{0} [P_{ij} - 1 /_{3} P_{kk} δ_{ij}] - \hat{β}_{0} [D_{ij} - 1/3 P_{kk} δ_{ij}] - k \overset{γ}{^}_{0} [S_{ij} - 1/3 S_{kk} δ_{ij}] (4.247)$ 其中， $D_{ij}$ 定义为 $D_{ij} = - ρ [\overline{u_{i}^{'} u_{m}} \frac{\partial u _{m}}{\partial x _{j}} + \overline{u_{j}^{'} u_{m}^{'}} \frac{\partial u _{m}}{\partial x _{i}}] (4.248)$ 平均应变率 $S_{ij}$ 在公式 4.244（第 101 页）中定义，而 $β_{RSM}^{*}$ 则由 $β_{RSM}^{*} = β^{*} f_{β}^{*} (4.249)$ 其中， $β^{*}$ 和 $f_{β}^{*}$ 的定义方式与标准 $k - ω$ 模型相同，分别采用公式 4.85（第 63 页）和公式 4.91（第 64 页）。唯一的区别在于， $f_{β}^{*}$ 的公式中使用了 640 这一数值，而非公式 4.85（第 63 页）中的 680。这些常数为... $α_{0} = \frac{8 + C _{2}}{11}, β_{0} = \frac{8 C _{2} - 2}{11}, γ_{0} = \frac{60 C _{2} - 4}{55}$ $C_{1} = 1.8, C_{2} = 0.52$ 上述公式无需使用粘性阻尼函数来解析近壁次层。然而，引入粘性阻尼函数[708]（第1098页）可能对某些流动的模型预测有所改善。由此导致的改动如下： $α = \frac{1 + α _{0} R e _{T} / R _{k}}{1 + R e _{T} / R _{k}}$ $β = β_{0} \frac{R e _{T} / R _{k}}{1 + R e _{T} / R _{k}}$ $γ = γ_{0} \frac{0.007 + R e _{T} / R _{k}}{1 + R e _{T} / R _{k}}$ $C_{1} = 1.8 [\frac{5/3 + R e _{T} / R _{k}}{1 + R e _{T} / R _{k}}]$ 其中， $α$ 、 $β$ 和 $γ$ 将替代公式 4.247（第 102 页）中的 $α_{0}$ 、 $β_{0}$ 和 $γ_{0}$ 。这些常数为 $R_{β} = 12, R_{k} = 12, R_{ω} = 6.20$ 在粘性模型对话框的 $k$ - ω选项下启用低Re修正，可以控制低Re粘性阻尼的包含。

4.11.4.5 应力-BSL模型

应力-BSL模型解决了基于基准（BSL） $k - ω$ 模型的尺度方程，从而消除了应力-ω模型中观察到的自由流敏感性。它在雷诺应力方程中使用了与应力-ω模型相同的压力-应变相关关系（公式4.247，第102页），但没有低雷诺数修正。系数 $β_{RSM}^{*}$ 等于 $β^{*}$ 。还有一个GEKO选项，允许EARSM与广义 $k$ – $ω$ （GEKO）模型结合（有关GEKO模型的更多信息，请参见广义k-ω（GEKO）模型，第70页）。

4.11.5 浮力对湍流的影响

由于浮力产生的项被建模为 $G_{ij} = - ρβ (g_{i} \overline{u_{j}^{'} θ} + g_{j} \overline{u_{i}^{'} θ}) (4.250)$ $\overline{U_{i}} \overline{θ} = \frac{μ _{t}}{P r _{t}} (\frac{\partial T}{\partial x _{i}}) (4.251)$ 其中， $t Pr$ 是能量的湍流普朗特数，默认值为 0.85。

利用热膨胀系数 $β$ 的定义，由公式 4.65（第 58 页）给出，对于理想气体，得到以下 $G_{ij}$ 的表达式： $G_{ij} = - \frac{μ _{t}}{ρP r _{t}} (g_{i} \frac{\partial ρ}{\partial x _{j}} + g_{j} \frac{\partial ρ}{\partial x _{i}}) (4.252)$

4.11.6 湍流动能建模

通常，当需要湍流动能来建模特定项时，它是通过取雷诺应力张量的迹来获得的： $k = \frac{1}{2} \overline{u_{i}^{'} u_{i}^{'}} (4.253)$ 如《壁面边界条件》（第105页）所述，Ansys Fluent 提供了一个基于 $ε$ 方程的雷诺应力模型的选项，以解决湍流动能的输运方程，从而获得雷诺应力的边界条件。在这种情况下，使用以下模型方程： $\frac{\partial}{\partial t} (ρ k) + \frac{\partial}{\partial x _{i}} (ρ k u_{i}) = \frac{\partial}{\partial x _{j}} [(μ + \frac{μ _{t}}{σ _{k}}) \frac{\partial k}{\partial x _{j}}] + \frac{1}{2} (P_{ii} + G_{ii}) - ρε (1 + 2 M_{t}^{2}) + S_{k} (4.254)$ 其中， $σ_{k} = 1.0$ ，而 $S_{k}$ 是一个用户定义的源项。方程4.254（第103页）可以通过对雷诺应力的模型方程（方程4.226，第98页）进行缩并得到。正如人们所料，它与标准 $k - ε$ 模型中使用的方程4.39（第50页）基本相同。

虽然方程4.254（第103页）被求解，但得到的 $k$ 值仅用于边界条件。在其他所有情况下， $k$ 都是从方程4.253（第103页）中获得的。然而，这是一个次要问题，因为无论采用哪种方法得到的 $k$ 值都应该非常相似。

4.11.7 耗散率的建模

对于基于 $ε$ 方程的雷诺应力模型，耗散张量 $ε_{ij}$ 被建模为 $ε_{ij} = \frac{2}{3} δ_{ij} (ρε + Y_{M}) (4.255)$ 其中， $Y_{M} = 2 ρε M_{t}^{2}$ 是根据Sarkar [566]（第1089页）模型引入的额外“膨胀耗散”项。该项中的湍流马赫数定义为 $M_{t} = \frac{k}{a ^{2}} (4.256)$ 其中， $a$ （即 $γ RT$ ）表示声速。当使用理想气体定律的可压缩形式时，可以进行这种可压缩性修正。

标量耗散率 $ε$ 通过一个类似于标准 $k - ε$ 模型中使用的模型传输方程来计算： $\frac{\partial}{\partial t} (ρε) + \frac{\partial}{\partial x _{i}} (ρε u_{i}) = \frac{\partial}{\partial x _{j}} [(μ + \frac{μ _{t}}{σ _{ε}}) \frac{\partial ε}{\partial x _{j}}] + C_{┓} \frac{1}{2} [P_{ii} + C_{┕} G_{ii}] \frac{ε}{k} - C_{└} ρ \frac{ε ^{2}}{k} + S_{ε} (4.257)$ 在 $σ_{ε} = 1.0, C_{┓} = 1.44, C_{└} = 1.92, C_{┕}$ 的情况下， $C_{┕}$ 是根据局部流动方向相对于重力矢量的函数来评估的，如《k-ε 模型中浮力对湍流的影响》（第 58 页）所述，而 $S_{ε}$ 是一个用户定义的源项。当雷诺应力模型与 $ω$ 或 BSL 方程耦合时，耗散张量 $ε_{ij}$ 被建模为... $ε_{ij} = \frac{2}{3} δ_{ij} ρ β_{RSM}^{*} kω (4.258)$ 其中， $β_{RSM}^{*}$ 在“压力-应变项建模”（第99页）的相关章节中定义。对于应力-ω模型，比耗散率 $ω$ 的计算方式与标准 $k - ω$ 模型相同，采用公式4.72（第62页），而对于应力-BSL模型，则使用来自基线（BSL） $k - ω$ 模型的公式4.102（第65页）。

4.11.8 湍流粘度的建模

对于基于 $ε$ 方程的雷诺应力模型，湍流粘度 $μ_{t}$ 的计算方式与 $k - ε$ 模型类似： $μ_{t} = ρ C_{μ} \frac{k ^{2}}{ε} (4.259)$ 其中 $C_{μ} = 0.09$ 。基于 $ω$ 方程（应力-omega）和 BSL 方程（应力-BSL）的雷诺应力模型使用方程 4.74（第 62 页）。

4.11.9 壁面边界条件

在 Ansys Fluent 中，RSM 模型需要为各个雷诺应力 $\overline{u_{i}^{'} u_{j}^{'}}$ 以及湍流耗散率 $ε$ （如果使用应力-omega 模型，则为 $ω$ ）设置边界条件。这些量可以直接输入，也可以从湍流强度和特征长度推导出来（参见用户指南中的雷诺应力模型）。在壁面处，Ansys Fluent 通过壁面函数计算雷诺应力和 $ε$ 的近壁值（参见标准壁面函数（第 138 页）、非平衡壁面函数（第 143 页）以及动量和能量方程的增强壁面处理（第 147 页））。Ansys Fluent 通过使用对数律和平衡假设，忽略应力输运方程中的对流和扩散，为雷诺应力应用显式壁面边界条件（方程 4.226（第 98 页））。采用局部坐标系，其中 $τ$ 为切向坐标， $η$ 为法向坐标， $λ$ 为副法向坐标，壁面相邻单元中的雷诺应力（假设为标准壁面函数或非平衡壁面函数）通过以下公式计算： $\frac{u _{τ}^{'2}}{k} = 1.098, \frac{u _{η}^{'2}}{k} = 0.247, \frac{u _{λ}^{'2}}{k} = 0.655, - \frac{u _{τ}^{'} u _{η}^{'}}{k} = 0.255 (4.260)$ 为了求得 $k$ ，Ansys Fluent 会解方程 4.254的输运方程。出于计算方便的考虑，该方程是全局求解的，尽管因此计算出的 $k$ 值仅在靠近壁面处需要；在远离壁面的区域， $k$ 直接通过使用方程 4.253（第 103 页）从正常的雷诺应力中获得。默认情况下，靠近壁面的雷诺应力值是使用从方程 4.260计算出的值固定的，而方程 4.226中的输运方程仅在主流区域求解。

另外，雷诺应力可以根据壁面剪切应力明确指定，而不是 $k$ ： $\frac{u _{τ}^{^{'} 2}}{u _{τ}^{2}} = 5.1, \frac{u _{η}^{^{'} 2}}{u _{τ}^{2}} = 1.0, \frac{u _{λ}^{^{'} 2}}{u _{τ}^{2}} = 2.3, - \frac{u _{τ}^{^{'}} u _{η}^{^{'}}}{u _{τ}^{2}} = 1.0 (4.261)$ 其中， $u_{τ}$ 是摩擦速度，定义为 $u_{τ} \equiv \frac{τ _{w}}{ρ}$ ，而 $τ_{w}$ 是壁面剪切应力。当选择此选项时， $k$ 输运方程不被求解。

在使用增强壁面处理作为近壁面处理时，Ansys Fluent 对雷诺应力方程应用零通量壁面边界条件。

4.11.10 对流热和质量传递建模

在 Ansys Fluent 的雷诺应力模型中，湍流热传递采用雷诺类比湍流动量传递的概念进行建模。因此，“建模”的能量方程如下： $\frac{\partial}{\partial t} (ρE) + \frac{\partial}{\partial x _{i}} [u_{i} (ρE + p)] = \frac{\partial}{\partial x _{j}} [(k + \frac{c _{p} μ _{t}}{P r _{t}}) \frac{\partial T}{\partial x _{j}} + u_{i} (τ_{ij})_{e ff}] + S_{h} (4.262)$ 其中， $E$ 表示总能量， $(τ_{ij})_{e ff}$ 是偏应力张量，定义为 $(τ_{ij})_{e ff} = μ_{e ff} (\frac{\partial u _{j}}{\partial x _{i}} + \frac{\partial u _{i}}{\partial x _{j}}) - \frac{2}{3} μ_{e ff} \frac{\partial u _{k}}{\partial x _{k}} δ_{ij}$ 涉及 $(τ_{ij})_{e ff}$ 的项表示粘性加热，在基于密度的求解器中始终会计算此项。在基于压力的求解器中，默认情况下不会计算此项，但可以在粘性模型对话框中启用。湍流普朗特数的默认值为0.85。您可以在粘性模型对话框中更改 $t Pr$ 的值。

湍流质量传输的处理方式类似，默认的湍流施密特数为0.7。此默认值可以在粘性模型对话框中进行更改。