电池容量随时间和重复的放电和充电循环而变化。容量衰减可能由许多不同的机制引起,例如过度充电、由于不良副反应导致的固体电解质界面 (SEI) 生长、机械裂纹等。 在Fluent中可以使用经验模型和基于物理的模型预测电池寿命。
经验模型可以考虑电池容量在长时间和短时间段内的衰减。电池的长期老化可以使用经验电池寿命模型估计,此模型中电池容量衰减效应被视为CFD前处理过程,其可用容量在CFD模拟之前更新;电池短期老化可以使用电池容量衰减模型,此模型中电池容量衰减可以指定为温度与倍率的函数。
基于物理的模型将基本的老化机理整合到 Newman P2D 模型中。该模型允许在独立模式下预测大量电力负载循环期间的电池老化过程。用户可以通过将独立模拟结果作为稳态配置文件插入,从而将 CFD 模拟中的老化效应视为预处理过程。
19.9.1 经验电池寿命模型
如果电池在经历反复放电和充电循环时处于活跃使用状态,则会发生电池容量损失,这种损失称为循环寿命损失。但即使不使用电池,由于长时间存放,其容量也可能会下降,这种损失称为日历寿命损失。
在 Fluent 中,使用 Arrhenius 类型的方程来计算日历寿命损失,并使用二维查找来计算循环寿命损失:
式中,为指前因子;为活化能;为电池的平均操作温度;为获得 Arrhenius 参数的参考温度;为时间;为时间指数因子;为容量修正因子。
一旦得到,就可以计算出 CFD 中使用的电池可用容量:
19.9.2 电池容量衰减模型
在CFD模拟中,也可以通过NTGK或ECM电池模型考虑电池容量衰减。Fluent 使用经验模型,用户可以在其中指定不同操作条件(温度和 C 速率)下的不同容量衰减因子,然后将指定的容量因子用于计算电池充电状态,如下所示:
- 在 NTGK 模型中,将公式 19.6(第 834 页)修改为以下形式以考虑容量衰减效应:
- 在 ECM 模型中,方程 19.9(第 836 页)中的第三个方程被替换为
19.9.3 基于物理的电池寿命模型
在 Fluent 中,基于物理的电池寿命模型考虑了固体电解质界面 (SEI) 生长和金属锂分解(镀锂)的老化机制。下图示意性地显示了电池充电过程中阳极颗粒表面发生的电化学反应。
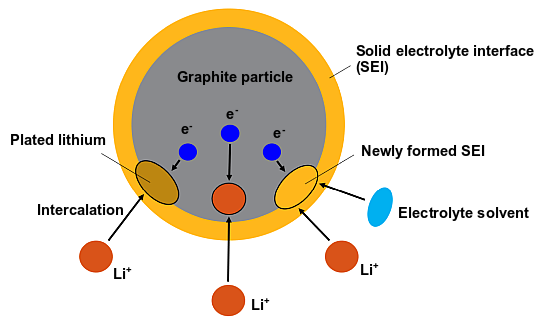
在基于物理的电池寿命模型中考虑了以下电化学反应:
- 插层反应
- SEI形成反应
- 锂沉积反应
当锂离子沉积到石墨表面并部分转化为金属锂(镀层)和部分转化为 SEI 时,就会发生反应。
SEI形成和锂沉积反应是与插层反应竞争的不必要的副反应。 这些副反应只在电池充电期间在阳极中突出和模拟。
SEI 生长和锂电镀导致电池老化主要通过以下影响:
- 部分锂库存损失形成 SEI 和镀锂,导致电池理论容量下降。
- SEI 和镀锂的表面膜增加了阳极石墨颗粒的表面电阻。
- SEI 和镀锂降低了阳极多孔介质的孔隙率,这进一步降低了电解质的有效电导率和扩散率。
为了模拟 SEI 生长和锂电镀,基于物理的电池寿命模型使用以下公式求解 SEI 浓度 Csei 的演变: 和使用以下公式计算镀锂浓度: 式中,为体积固体/电解质界面面积;为法拉第常数;为SEI生成反应在活性材料孔壁面中的电流通量 ;为锂沉积反应在活性材料孔壁面中的电流通量;是成为SEI的沉积锂的分数。
由于SEI和镀锂反应的控制方程没有空间项,其演化仅依赖于局部源项,即局部副反应的电流通量。这些源项由阴极Tafel表达式表示: 及: 式中:为反应速率常数;为碳酸乙烯酯(EC)的表面浓度;及为SEI和镀锂副反应的阴极电荷转移系数;为普适气体常数;为电池温度;及为SEI和镀锂副反应的过电位;为反应交换电流密度,模拟中作为常数。
EC的表面浓度由EC穿过表面膜的扩散通量确定: 式中,为主体电解液中EC的浓度;为EC的扩散系数;为膜厚度。
与公式(19.19)类似,副反应(SEI形成和锂沉积)的超电位计算如下: 式中,及分别为固体(电极)和电解质相的电势;及分别由于锂嵌入反应和副反应的活性材料孔壁电流通量;为副反应平衡电势;为电阻。
表面膜的物理性质(厚度和电阻)表示为SEI和镀覆的锂浓度的函数:
阳极电解质孔隙率随着表面膜的生长而降低,并计算如下: 在公式19.60至公式19.62中,使用了以下符号:
及分别为SEI和镀锂的分子量;为阳极活性物质的颗粒半径;为SEI离子电导率;为新鲜电池电解质材料的体积分数;为新鲜电池活性物质的体积分数;及分别为SEI和镀锂的密度。
在实际的Newman的P2D模型模拟中,通过电负载循环对电池老化进行模拟,基于物理的电池寿命模型在独立模式下的电极秤上求解(有关更多信息,请参见Fluent用户指南中的模拟电池老化过程(独立模式))。此外,独立模拟结果可包括在3D CFD模拟中以说明电池老化效应。在这种情况下,老化效应被视为在时间上冻结。更具体地,在E-Chem模型计算期间,SEI和镀覆锂浓度(其确定锂存量损失)、表面膜电阻和阳极上的电解质孔隙率的分布作为稳态分布被包括在Newman P2D模型中。在受计算能力约束的实际CFD模拟中,模拟时间远小于电池寿命的时间尺度。这种时间尺度的宽间隔证明了时间冻结老化效应的合理性。