在考虑线性弹性结构模型时,假设了应变与位移之间的线性关系。这种假设仅在位移概念较小时才适用。相反,大位移意味着初始几何形状的显著变化,因此必须在求解算法中引入几何非线性(参见 Bhatti [59](第 1060 页)以获取更多详细信息)。
16.5.1 有限元几何非线性
非线性弹性结构模型考虑了几何非线性,以模拟大变形。在大变形情况下,参考构型基于初始构型,并且所有量都采用总拉格朗日公式进行表述。因此,刚度矩阵成为位移的函数。这种公式中的主要概念之一是引入变形梯度公式,这是在大位移公式中描述应变的主要工具。
总之,非线性弹性结构模型的主要概念包括:
-
大应变
-
刚度矩阵是位移的函数
-
应变与位移之间的非线性关系
-
总拉格朗日公式
初始状态与变形状态之间的关系表示为:
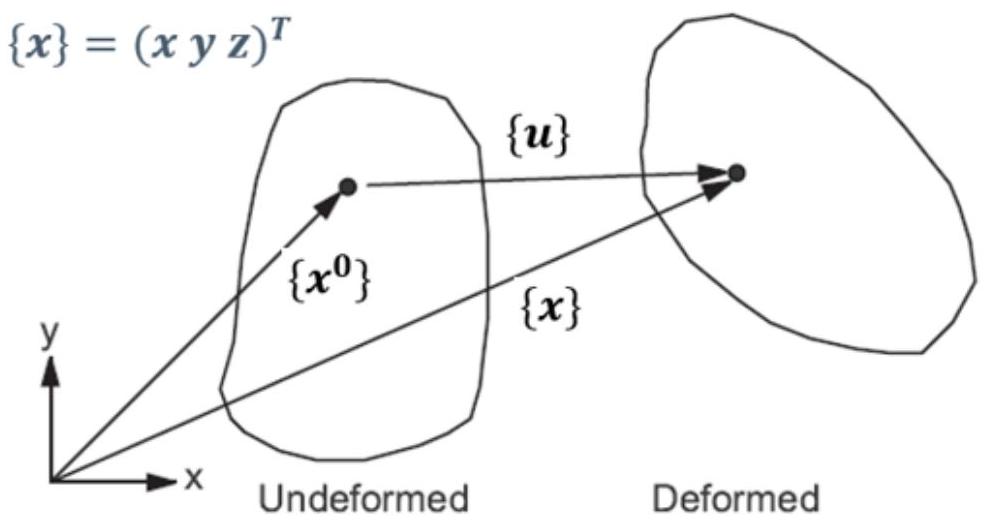
从数学上讲,变形通过变形张量表示:
16.5.2 有限元非线性离散化
几何非线性离散化的主要任务是构建刚度矩阵。节点位移增量的求解方程的整体离散化基于切线单元方程:
在前述方程中,总刚度矩阵由两个部分构成:当前刚度矩阵和应力刚度矩阵。当前刚度矩阵定义为:
应力(几何)刚度矩阵定义如下:
在哪儿
应变-位移矩阵
变形梯度矩阵
本构矩阵
第二皮奥拉-基尔霍夫应力张量
单元体积
16.5.3 本构方程
为了完全封闭有限元非线性离散化(第832页)中概述的方程,必须定义一个本构方程,以确定应力与应变之间的关系。对于大位移问题,假设格林-拉格朗日应变与第二皮奥拉-基尔霍夫应力之间存在某种关系。因此,可以定义一阶张量形式为:
向量矩阵形式如下:
第二类皮奥拉-基尔霍夫应力矢量定义如下:
格林-拉格朗日应变矢量定义如下:
构成矩阵 将形成一个 的矩阵张量。此处不涉及大应变情况下构成矩阵的完整推导,但我们仅指出,默认情况下使用可压缩的超弹性 Neo-Hookean 材料作为非线性弹性的模型。Neo-Hookean 模型因其通用性以及作为通常线性各向同性模型(胡克定律)向大变形的自然延伸而被首选。
16.5.4 非线性系统的瞬态方案
非线性系统的默认瞬态方案与线性弹性所用的方案相同:Newmark 方法。非线性系统瞬态运动的半离散方程给出如下:
需要注意的是,内部载荷 依赖于当前时刻 的位移 。通过牛顿-拉弗森方法,可以将上述方程线性化,得到以下形式:
残差向量
位移增量
切线刚度矩阵
以及
相同的逻辑也适用于与非线性弹性模型结合使用的后向欧拉方案。