本节介绍了在Ansys Fluent通用多相流模型框架下的质量传输建模(即欧拉多相流、混合多相流、VOF多相流)。Ansys Fluent中可以模拟多种质量传输过程。你可以使用Ansys Fluent中提供的模型(例如Ansys Fluent的空化模型),或者通过用户自定义函数定义自己的质量传输模型。更多关于通过用户自定义函数进行质量传输建模的信息,请参见UDF-Prescribed Mass Transfer(第752页)和《Fluent定制手册》。
关于质量传输的信息在以下小节中呈现:
- 14.7.1. 质量传输引起的源项
- 14.7.2. 单向恒定速率质量传输
- 14.7.3. UDF-Prescribed质量传输
- 14.7.4. 空化模型
- 14.7.5. 蒸发-冷凝模型
- 14.7.6. 半机制沸腾模型
- 14.7.7. 相间物种质量传输
14.7.1 质量传输引起的源项
Ansys Fluent仅在动量、物种和能量方程中添加质量传输的贡献。对于其他标量,如湍流或用户自定义标量,不添加源项。
设 为单位体积内从相 的第 种物质到相 的第 种物质的质量传输速率。如果某个相没有与其关联的混合物材料,则质量传输将涉及整个相。
14.7.1.1 质量方程
在单元中,相 的质量源项的贡献为...
而对于相位则是
14.7.1.2 动量方程
对于VOF或混合模型,不存在动量源。
对于Eulerian模型,在相的单元中的动量源为
而对于相位 来说,
14.7.1.3 能量方程
对于所有多相流模型,以下能量源项均被加入。
相 在单元格中的能量源项为
而对于相位 则是:
其中, 和 分别表示相 中物种 和相 中物种 的生成焓。 和 之间的差异即为潜热。
14.7.1.4 物种方程
对于相 中的物种 ,其在单元格中的物种源项为...
对于相态 中的物种 而言,
14.7.1.5 其他标量方程
湍流量和其他标量没有添加源/汇项。由于质量传递导致的这些标量量的传递可以通过用户定义的源项来建模。
14.7.2 单向恒定速率质量传递
单向质量传递模型定义了从相 到相 的每单位体积的正质量流率:
以下文本的中文翻译:
表示粒子收缩或膨胀的恒定速率,例如液体液滴燃烧的速率(单位为 时间单位)。
如果相 是混合材料,并且为相 的物种 定义了质量传递机制,
其中, 表示相 中物质 的质量分数。
14.7.3 UDF-规定的质量传递
由于没有普遍适用的质量传递模型,Ansys Fluent 提供了一个 UDF,您可以使用它输入不同类型的质量传递模型,例如蒸发、冷凝、沸腾等。请注意,在使用此 UDF 时,Ansys Fluent 会自动将源项贡献添加到所有相关的动量和标量方程中。这一贡献基于以下假设:“生成”或“消耗”的质量将具有与其生成或消耗的相相同的动量和能量。如果您希望直接将源项输入到动量、能量或标量方程中,那么适当的路径是使用所有方程的用户定义源项的 UDF,而不是质量传递的 UDF。有关多相流中基于 UDF 的质量传递的更多信息,请参阅 Fluent 定制手册。
14.7.4 空化模型
在恒定温度下,液体可能承受降低的压力,该压力可能低于饱和蒸汽压。通过在恒定温度下降低压力来破坏液体的过程称为空化。液体中还含有不可冷凝(溶解或吸入)气体的微小气泡,或核,在压力降低的情况下可能增长并形成空穴。在这样的过程中,低压/空化区域会发生非常大且陡峭的密度变化。
本节提供有关 Ansys Fluent 中使用的以下空化模型的信息:
-
Zwart-Gerber-Belamri 模型 [741](第 1100 页)
-
Schnerr 和 Sauer 模型 [585](第 1091 页)(默认)
此外,Ansys Fluent 提供了由 Singhal 等人 [600](第 1091 页)开发的专家空化模型,该模型自版本 6.1 起就已可用。然而,由于收敛性挑战,目前不推荐使用此模型。有关此模型的描述,请参见专家空化模型(第 757 页)。
在标准的两相空化模型中,做出了以下假设:
-
所研究的系统必须由液体和蒸汽相组成。
-
假设液体和蒸汽相之间存在质量转移。空化模型中同时考虑了气泡形成(蒸发)和崩溃(冷凝)。
-
对于空化模型,Ansys Fluent 将正质量转移定义为从液体到蒸汽。
-
空化模型基于描述液体中单个蒸汽气泡生长的雷利-普莱塞特方程。
-
空化模型中使用的输入材料属性可以是常数、温度的函数或用户自定义的。
14.7.4.1 空化模型的局限性
Ansys Fluent 中的空化模型存在以下局限性:
-
Zwart-Gerber-Belamri 和 Schnerr 与 Sauer 模型默认情况下不考虑非冷凝气体的影响。
-
由于以下原因,不建议将显式 VOF 与空化模型结合使用:
-
显式 VOF 在每个时间步长内只求解一次,因此质量转移率(这是压力、温度和体积分数等解变量的函数)也仅在每个时间步长内评估一次。这可能无法得到与使用隐式公式获得的结果一致的结果。建议在每次迭代中求解体积分数,这可以通过在 对话框中的专家选项启用。
-
显式VOF可能与诸如Geo-Reconstruct和CICSAM等锐化方案不稳定。您应使用Sharp/Dispersed或Dispersed界面建模选项,这些选项提供了用于体积分数的扩散界面捕捉离散化方案,如QUICK、HRIC和Compressive。
-
显式VOF不包含任何针对增加稳定性的空化特定数值处理。
-
在使用隐式VOF公式时,默认情况下会因湍流效应而增加数值扩散。这种增加的扩散提高了求解稳定性,但会对界面精度产生不利影响。如果界面锐度是一个关注点,您可以按照《Fluent用户指南》中关于空化机制的描述禁用扩散。
14.7.4.2 蒸汽输运方程
采用多相空化建模方法,一个基本的二相空化模型包括使用标准粘性流动方程来控制混合物(混合模型)或相(欧拉多相)的输运,以及一个传统的湍流模型(k-ε模型)。在空化中,液体-蒸汽质量转移(蒸发和凝结)由蒸汽输运方程控制:
其中
蒸汽相
蒸汽体积分数
蒸汽密度
蒸汽相速度
与蒸汽泡生长和崩塌分别相关的质量传递源项
在公式14.580(第754页)中,项和考虑了液体和蒸汽相之间的质量传递,这与空化有关。在Ansys Fluent中,它们基于描述液体中单个蒸汽泡生长的Rayleigh-Plesset方程进行建模。
14.7.4.3 气泡动力学考虑
在大多数工程情况下,我们假设有大量的核用于空化起始。因此,我们的主要关注点是正确考虑气泡的生长和崩塌。在流体和气泡之间没有速度滑移的流动液体中,气泡动力学方程可以从广义Rayleigh-Plesset方程推导出来,如[78](第1061页)所示。
其中,
气泡半径
液体表面张力系数
液体密度
液体运动粘度
气泡表面压力
当地远场压力
忽略二阶项和表面张力力,方程14.581(第754页)简化为
该方程提供了一种物理方法,用于将气泡动力学效应引入空化模型。它也可以被视为一个关于空穴传播的方程,从而涉及混合物密度的变化。
14.7.4.4 Schnerr 和 Sauer 模型
为了推导出净相变率的表达式,Schnerr 和 Sauer [585](第 1091 页)使用了以下两相连续性方程:
液相:
气相:
混合物:
其中,
液相
混合物密度(与相体积分数和密度相关的函数)
混合物密度 定义为
结合方程14.583(第755页)、方程14.584(第755页)以及方程14.585(第755页),可以得到混合密度与蒸汽体积分数之间的关系:
气相体积分数 可以与气泡数量密度 及气泡半径 相关联,如下所示:
利用公式14.582(第755页),并结合公式14.583(第755页)、公式14.584(第755页)、公式14.587(第755页)以及公式14.588(第755页),最终得到了净相变速率的表达式。
其中,
质量传递速率
气泡半径
将方程14.589(第755页)与方程14.602(第758页)和方程14.595(第756页)进行比较,显然不同于前两种模型,Schnerr和Sauer模型中的质量传递速率与 成正比。此外,函数 具有一个有趣的性质,即当 和 时趋近于零,并在两者之间达到最大值。在该模型中,唯一需要确定的参数是每单位液体体积内的球形气泡数量。如果你假设气泡不会产生或消失,那么气泡数量密度将是恒定的。因此,成核点体积分数和平衡气泡半径的初始条件足以从方程14.588(第755页)中确定气泡数量密度 ,然后通过方程14.589(第755页)确定相变。
模型的最终形式如下:
当 时,
当 时,
其中, 和 分别是蒸发和冷凝的经验校准系数,默认值分别为1和0.2。您可以根据《Fluent用户指南》中“质量转移机制”一节所述,通过专家文本命令选项更改这些系数。
14.7.4.5 Zwart-Gerber-Belamri模型
假设系统中所有气泡大小相同,Zwart-Gerber-Belamri [741](第1100页)提出,单位体积内的总相间质量转移速率 是根据气泡数密度 和单个气泡的质量变化速率计算得出的:
蒸汽体积分数 与气泡数密度及气泡半径的关系如下:
将 的值从公式 14.593(第 756 页)代入公式 14.594(第 756 页),我们得到了净质量转移的表达式:
比较方程14.595(第756页)和方程14.602(第758页),你会发现差异仅在于质量转移率中的密度项。在方程14.595(第756页)中,单位体积质量转移率仅与蒸汽相密度相关。与方程14.602(第758页)不同,在此模型中,与液相和混合物密度无关。
正如方程14.602(第758页)所示,方程14.595(第756页)是在假设气泡生长(蒸发)的情况下推导出来的。为了将其应用于气泡崩溃过程(凝结),我们采用了以下通用公式:
其中 是一个经验校准系数。虽然最初是从蒸发推导出来的,但公式 14.596(第 757 页)仅在冷凝情况下表现良好。如果应用于蒸发,它在物理上是不正确的,并且在数值上不稳定。根本原因是其中一个关键假设是空化气泡不相互作用。这仅在空化的最初阶段是合理的,即空化气泡从成核点生长时。随着蒸汽体积分数的增加,成核点密度必须相应降低。为了模拟这一过程,Zwart-Gerber-Belamri 提出在公式 14.596(第 757 页)中用 替换 。于是,该空化模型的最终形式如下:
如果
如果 ( P \geq P_v )
其中,
气泡半径
成核点体积分数
蒸发系数
凝结系数
14.7.4.6 专家空化模型
Singhal 等人提出的模型是一种针对特定应用的专家模型。它可以用来考虑不可凝气体的效应。不可凝气体的质量分数被假定为已知的常数。
以下提供了该模型的理论背景及其局限性。
14.7.4.6.1 Singhal 等人模型的局限性
Singhal 等人模型存在以下局限性:
-
Singhal 等人模型仅适用于单一空化过程。也就是说,当通过 Singhal 等人模型定义质量转移时,只能有一个单一的液体流体经历空化。这种液体可以是混合相中的一个相或一个物种。
-
Singhal 等人模型要求主相为液体,次相为蒸汽。该模型仅与多相混合模型兼容。
-
Singhal 等人模型不能与欧拉多相模型一起使用。
-
Singhal 等人模型与 LES 湍流模型不兼容。
14.7.4.6.2 Singhal 等人模型理论
此空化模型基于Singhal等人[600](第1091页)开发的“完全空化模型”。它考虑了所有一阶效应(即相变、气泡动力学、湍流压力波动和不可凝气体)。该模型能够处理多相(N相)流动或涉及多相物质输运的流动,液体与气相之间的滑移速度效应,以及液体和气相的热效应和可压缩性。空化模型可与混合多相模型结合使用,无论是否考虑滑移速度。然而,通常更倾向于使用无滑移速度的混合模型来求解空化问题;如果问题表明各相之间存在显著滑移,则可以开启滑移速度选项。
蒸汽体积分数与气泡数密度和气泡半径的关系如下:
混合物密度与蒸气体积分数之间的关系可表示为:
净相变率 的表达式计算如下:
此处, 代表汽化速率,即方程 14.580(第 754 页)中的源项 。除了 以外,所有项均为已知常数或依赖变量。在没有普遍适用的气泡数密度估算模型的情况下,相变速率表达式被改写为以气泡半径 为变量的形式,如下所示:
方程14.602(第758页)表明,单位体积质量传递速率不仅与蒸汽密度有关,还与液体密度和混合物密度有关。由于方程14.602(第758页)直接从相体积分数方程推导得出,因此它是精确的,并且应该准确地表示空化过程中从液相到汽相的质量传递(气泡生长或蒸发)。尽管预计气泡崩溃或冷凝的质量传递计算与气泡生长不同,但方程14.602(第758页)通常被用作模拟气泡崩溃的第一近似。在这种情况下,方程右侧通过使用压力差的绝对值进行修改,并被视为汇项。
需要注意的是,在实际的空化模型中,通常将局部远场压力取为与单元中心压力相同。在没有溶解气体、质量传输和粘性阻尼的情况下,气泡压力等于饱和蒸汽压力,即。
其中,
气泡压力
饱和蒸汽压力
基于方程14.602(第758页),Singhal等人[740](第1100页)提出了一种模型,其中蒸汽质量分数是传输方程中的因变量。该模型还适用于单相公式,其中控制方程为:
其中,
蒸汽质量分数
非冷凝气体质量分数
质量交换速率由以下方程给出:
若
如果 ( P > P_v )
饱和压力通过估算局部湍流压力波动值进行修正:
常数取值为 和 。在此模型中,假定液-汽混合物是可压缩的。同时,也考虑了湍流和不可凝气体的影响。
14.7.4.7 湍流因子
可以选择性地考虑湍流对阈值压力的影响。在所有空化模型中,阈值压力的计算依据 Yang 等人 [127] (第 1064 页) 所述:
其中, 和 分别表示液相密度和湍流动能。建议的coeff值为0.39,此值为默认使用。
14.7.4.8 空化模型的额外指导原则
在实际应用空化模型时,多个因素会严重影响数值稳定性。例如,入口与出口之间的高压差、液相与气相比例的巨大差异以及液体与气体之间的大相变率,这些都对解的收敛性产生不利影响。此外,不良的初始条件往往会导致不真实的压力场和意外的空化区域,一旦出现,通常难以纠正。在选择空化模型并处理潜在的数值问题时,您可以考虑以下因素/提示:
- 空化模型的选择
在Ansys Fluent中,有三种可用的空化模型。Zwart-Gerber-Belamri模型和Schnerr and Sauer模型采用了与Singhal et al.模型完全不同的数值处理流程。从数值角度来看,这两种模型都较为稳健且收敛迅速。因此,强烈建议您使用Schnerr and Sauer模型或Zwart-Gerber-Belamri模型。尽管Singhal et al.模型在物理上与其他两种相似,但数值稳定性较差,使用难度更高。
- 求解器的选择
在Ansys Fluent中,分离式(SIMPLE、SIMPLEC和PISO)和耦合式压力基求解器均可用于空化模拟。通常,耦合求解器更为稳健且收敛速度更快,特别是在旋转机械(如液泵、诱导轮、叶轮等)中的空化流动。然而,对于燃料喷射器应用,分离式求解器在与Schnerr and Sauer模型和Zwart-Gerber-Belamri模型结合使用时也表现出色。
关于Singhal等人提出的模型,由于耦合求解器并未显示出显著优势,建议采用分离求解器。
- 初始条件
虽然不需要特别的初始条件设置,但我们建议始终将蒸汽分数设置为入口值。压力应接近入口和出口中的最高压力,以避免意外的低压和空化点。通常情况下,Schnerr和Sauer以及Zwart-Gerber-Belamri模型足够健壮,无需特定的初始条件。但在某些非常复杂的情况下,在形成大量空腔之前获得一个真实的压力场可能是有益的。这可以通过先获得单相液体流动的收敛/接近收敛解,然后启用空化模型来实现。同样,Singhal等人提出的模型对初始条件更为敏感,通常需要上述处理。
- 压力离散化方案
对于一般的多相流,在空化应用中按以下顺序使用以下压力离散化方案更为理想:
-
体积力加权
-
二阶
标准和线性方案在复杂的空化流动中通常效果不佳,应避免使用。
-
松弛因子
-
Schnerr和Sauer以及Zwart-Gerber-Belamri模型
默认设置通常效果良好。为了提高数值效率,以下值可能被推荐:
蒸汽的松弛因子为0.5或更高,除非解发散或所有残差过度振荡。
密度和汽化质量可以松弛,但通常将它们设置为1。
对于分离求解器,压力的松弛因子应不低于动量方程的值。
对于耦合求解器,Courant数(200)在某些复杂的3D情况下可能需要降低到20-50。
- Singhal等人模型
通常建议对动量方程使用较小的松弛因子,一般在0.05 - 0.4之间。压力修正方程的松弛因子通常应大于动量方程的松弛因子,例如在0.2 - 0.7范围内。密度和汽化质量(汽化方程中的源项)也可以通过松弛来改善收敛性。通常,密度的松弛因子设定在0.3到1.0之间,而对于汽化质量,0.1到1.0之间的值可能是合适的。在某些极端情况下,所有方程可能需要更小的松弛因子。
-
Singhal等人模型的特殊提示
-
非冷凝气体
非冷凝气体通常存在于液体中。即使是非常少量的非冷凝气体(例如,15 ppm)也可能对物理结果和解的收敛特性产生显著影响。通常应避免非冷凝气体质量分数为零的值。在某些情况下,如果液体经过非冷凝气体净化,可以使用更小的值(例如,)来替代默认值。实际上,在许多情况下,非冷凝气体的高质量分数可能会增强数值稳定性并导致更真实的结果。特别是在某温度下液体的饱和压力为零或非常小时,非冷凝气体在数值和物理上都将发挥关键作用。
- 依赖变量的限制
在许多情况下,将压力上限设定为合理值,可以在求解初期极大地帮助收敛。建议在可能的情况下始终限制最大压力。Ansys Fluent 默认的最大蒸汽压力限制值是考虑湍流和热效应后的当地蒸汽压力的五倍。你可以使用专家文本命令选项,如 Fluent 用户指南中关于质量传递机制所述,来更改蒸汽压力比(即最大蒸汽压力限制与当地压力的比值)。
- 压力修正方程的松弛因子
对于空化流动,为压力修正方程引入了一个特殊的松弛因子。默认情况下,该因子设为 0.7,适用于大多数情况。然而,在一些非常复杂的情况下,你可能会遇到 AMG 求解器的分歧。在这种情况下,该值可能需要降低至不低于 0.4。你可以通过输入文本命令来设置此松弛因子的值。更多信息,请联系你的 Ansys Fluent 技术支持工程师。
14.7.4.9 扩展空化模型能力
当发生空化时,在许多实际应用中系统内存在其他气体物种。例如,在通气超空化车辆中,空气被注入液体中以稳定或增加车辆表面的空化。在某些情况下,来流是液体与某些气体物种的混合物。为了预测这类空化流动,基本的二相空化模型必须扩展为多相(N 相)流动,或一个多相物种输运空化模型。
14.7.4.9.1 N 相空化模型
多相空化模型是基于三种基本的两相空化模型向多相流动的扩展。在模拟N相流动时,可以在以下假设条件下在计算系统中添加多个液体和气体相:
-
质量转移(空化)仅在液体和蒸汽相之间发生。
-
基本的两相空化模型仍用于模拟液体和蒸汽之间的相变。
-
在Singhal等人模型中,可以包括预定义的非冷凝气体。要从系统中排除非冷凝气体,质量分数必须设置为0,并且非冷凝气体必须通过单独的可压缩气体相进行建模。
-
对于非空化相,在Zwart-Gerber-Belamri和Schnerr and Sauer模型中,控制蒸汽相的一般输运方程是体积分数方程,而在Singhal等人模型中,求解质量转移方程,并且蒸汽必须是第二相。
14.7.4.9.2 多相物种输运空化模型
多相物种输运方法的详细描述可以在《多相流中的物种输运建模》(第778页)中找到。多相物种输运空化模型可以总结如下:
-
所有适用于多相空化模型的假设/限制在这里都适用。
-
液体和蒸汽相/物种之间的质量转移由基本空化模型建模。
-
对于具有多个物种的相,该相与其他相共享相同的压力,但每个物种都有其自己的压力(即分压)。因此,方程14.605(第759页)中使用的蒸汽密度和压力是蒸汽的分密度和分压。
14.7.5 蒸发-冷凝模型
Ansys Fluent 通过蒸发-冷凝实现相间质量转移时,采用两种模型之一。在使用VOF和混合物公式时,采用Lee模型。在使用欧拉公式时,可以选择Lee模型或热相变模型。
14.7.5.1 Lee模型
Lee模型[350](第1077页)是一个基于物理机制的模型。它与混合物和VOF多相模型一起使用,如果将使用总体界面传热系数模型(而不是双阻力模型),也可以在欧拉多相模型中选择。在Lee模型中,液-汽质量转移(蒸发和冷凝)由蒸汽传输方程控制:
其中,
表示气相,
表示气相体积分数,
表示气相密度,
表示气相速度,
和 分别表示由于蒸发和冷凝引起的质量传递速率。这些速率使用单位 。
如公式 14.608(第 763 页)右侧所示,Ansys Fluent 将蒸发-冷凝问题中的正质量传递定义为从液相到气相。
根据以下温度区间,质量传递可以描述如下:
如果 (蒸发):
若 (凝结):
coeff 是一个需要精细调谐的系数,可以解释为弛豫时间。 和 分别是相体积分数和密度。能量方程的源项可以通过将质量转移速率乘以潜热来获得。
考虑 Hertz-Knudsen 公式 [239](第 1070 页)[315](第 1075 页),该公式基于平坦界面上的动力学理论给出了蒸发-凝结通量:
通量具有单位 , 表示压力, 表示温度, 是通用气体常数。系数 是所谓的适应系数,它表示进入液体表面并被该表面吸附的蒸汽分子部分。 代表蒸汽侧界面处的蒸汽分压。克拉佩龙-克劳修斯方程描述了饱和条件下压力与温度之间的关系(通过等式化蒸汽和液体化学势获得)。
和 分别是蒸汽和液体的密度倒数(即单位质量的体积)。 是潜热 。
基于这个微分表达式,我们可以从接近饱和条件的压力变化中获得温度变化。
图14.13:稳定相图
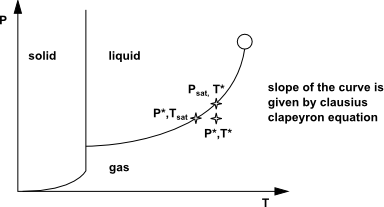
只要 和 接近饱和条件,克劳修斯-克拉佩龙方程就会产生以下公式:
利用这一关系式在上述Hertz-Knudsen方程中,得出[645](第1094页)。
因子 是根据适应系数和蒸气的物理特性定义的。在接近平衡条件下, 趋近于 1.0。
在欧拉多相流模型和混合多相流模型中,流动状态被假设为分散的。例如,如果我们假设所有蒸气泡具有相同的直径,那么界面面积密度可以通过以下公式给出:
其中, 表示气泡直径 ,而相源项 应采用以下形式:
从上述方程中,,即弛豫时间的倒数(单位为1/秒),被定义为
这导致了方程14.609(第763页)中定义的蒸发过程的最终表达式。它可以隐式地作为一个源项处理在相守恒方程中。
对于冷凝过程,可以得到类似的表达式。在这种情况下,我们考虑在连续蒸汽相中的小液滴,即使你的主要相是液体。
请注意,理论上冷凝和蒸发的系数coeff应该是不同的。此外,理论表达式基于一些强假设:
- 平坦界面
- 分散状态,直径恒定
- 已知的
气泡直径和适应系数通常不是很清楚,这就是为什么必须对系数coeff进行微调以匹配实验数据。默认情况下,蒸发和冷凝的系数均为0.1。然而,在实际情况下,coeff的数量级可以高达。
14.7.5.2 热相变模型
当使用欧拉多相模型并采用计算相间传热系数的双阻力法(双阻力模型(第703页))时,热相变模型可用于蒸发-冷凝过程。
将方程14.389(第703页)和方程14.390(第703页)应用于液-汽对时,得到:
- 从界面到液相:
从界面到气相:
其中, 和 分别代表液相和气相的传热系数, 和 分别代表液相和气相的焓值,而 和 则是缩放因子。默认情况下, 和 均设定为1。界面温度 的确定考虑了热力学平衡。
忽略表面张力对压力的影响,我们可以假设 等于 ,即饱和温度。
由于相界面既不能储存热量也不能储存物质,因此整体热平衡必须得到满足:
从上述方程可以看出,液体通过蒸发向气相的质量转移可以表示为:
为了正确计算相变焓值 和 ,需要考虑到由于两相间的潜热引起的静态焓的不连续性,以及从任一相到相界面的热传递。采用 Prakash 公式 [532](第 1088 页),将主流体焓带出流出相,并将饱和焓带入流入相,我们有:
如果 (蒸发,液相为流出相):
若 (冷凝过程,液相为进相):
这导致了一个在物理上和数值上都稳定的形式。这意味着方程14.621(第766页)的分母不为零,其值大于或等于潜热:
需要注意的是,在存在质量传递的情况下, 和 是各相的总焓,可以用一般形式表示为:
其中, 是参考温度, 是在 下的标准态焓。方程 14.625 (第 766 页) 适用于各相以及各相中的物种。
请注意,在热相变模型中,蒸发-凝结质量传递过程完全由相间传热过程和整体热平衡控制。与 Lee 模型不同,质量传递系数不需要校准。因此,通常建议在模拟蒸发-凝结过程时使用欧拉多相公式和双阻力传热方法。
14.7.6 半机制沸腾模型
在核工业和汽车工业等多个工业领域中,研究沸腾传热非常重要。已经提出了几种沸腾模型用于预测高压应用中的传热。然而,对于低压汽车系统,基于特定实验相关性的高压沸腾模型可能不可靠且数值不稳定。
为了模拟低压下的欠热核沸腾,通常将整体蒸发/凝结现象与由于沸腾引起的壁面传热增强相结合。在 Ansys Fluent 中,Lee 模型用于捕捉壁面附近和整体域中的相变过程。壁面传热增强通过 Chen [133] (第 1064 页) 的经验相关性进行建模。
图 14.14: 沸腾曲线
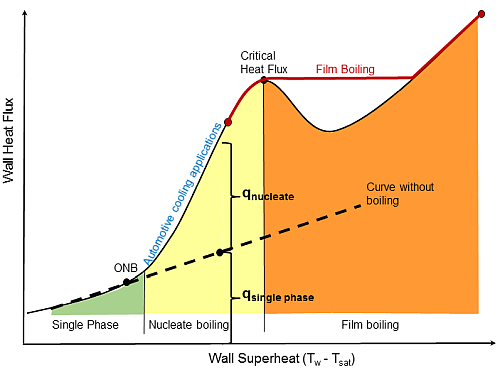
Chen [104] (第 1063 页) 提出了垂直管道的流动沸腾相关性,其中有效壁面热流表示为核沸腾热流和强制对流热流的加权和。Chen 的相关性基于以下假设:
-
蒸发过程中形成的蒸汽增大了液体速度,因此,相对于单相液体流动,对流换热贡献得到了增强。
-
对流部分抑制了沸腾点的成核,从而减少了核沸腾的贡献。
Chen 提出的有效壁面热通量 表达为:
其中
为强制对流增强因子
和 分别为单相和核沸腾的传热通量乘数
为单相传热通量
为核沸腾传热通量
为核沸腾抑制因子
Kutateladze [329](第1076页)提出了一种使用渐近幂律修正的有效传热通量 的形式,其表达式为:
其中, 是幂律叠加常数。将 设为 1 时,会产生单相热流和核沸腾热流的线性叠加,正如 Chen 所提出的那样。Kutateladze 提出了一种渐近方法,其中 。随着 值的增大,有效热流倾向于变得大于单相热流和核沸腾热流。
公式 14.626(第 767 页)中的单相热流 由以下公式给出:
以下是翻译成中文的文本:
在哪里
公式14.626(第767页)中的核态沸腾热流密度 由以下公式给出:
哪里
在上述方程中,
和 分别为单相和核沸腾的传热系数,
为壁面温度,
为边界单元温度,
为饱和温度。
有效单相传热系数 的计算公式如下:
其中, 和 分别是液相和气相的单相传热系数, 是润湿分数(液体润湿壁面的部分)。
核沸腾传热系数 采用 Foster 和 Zuber 关联式进行计算:
其中
液体的热导率
液体的比热容
液体的密度
液体的粘度
蒸汽的密度
表面张力系数
潜热
和 分别对应壁温和饱和温度的饱和压力
Chen 提出了强制对流增强因子 的形式,如 [319] (第 1075 页) 所示:
马丁内利参数 用于考虑两相效应对对流的影响,其定义如下:
其中, 表示蒸汽品质(质量分数)。
核沸腾抑制因子 由以下公式给出:
其中, 是由于强制对流引起的抑制因子,而 是由于欠热度效应引起的抑制因子。根据Steiner等人[633](第1093页)的提议, 的计算如下:
在公式14.635(第769页)中,的表达式采用了Butterworth等人[89](第1062页)提出的公式:
其中, 表示修正后的两相雷诺数尺度:
在这里,液体参考雷诺数的计算公式如下:
以下是翻译成中文的文本:
参考温度 下的液体密度
参考温度 下的液体粘度
参考速度
长度尺度
有关如何使用半机制沸腾模型的信息,请参阅《Fluent 用户指南》中的“包含半机制沸腾”部分。
14.7.7 相间物种质量传递
您可以使用 Fluent 来模拟相间物种质量传递。相间物种质量传递可以根据相中传输物种的浓度梯度,在相界面(气体与液体之间,或液体与固体之间)之间发生。例如:
-
液体蒸发到包含其蒸气的气体混合物中,如液态水蒸发到空气和水蒸气的混合物中。
-
溶解气体从气体混合物中被液体吸收/溶解,例如水从空气中吸收氧气。
相间物种质量传递可以在混合模型或欧拉模型中求解,但需满足以下条件:
-
两相均由至少包含两种物种的混合物组成,且至少有一种物种在两相中均存在。
-
两种混合物相处于接触状态,并由界面分隔。
-
物种质量传递只能发生在从一相到另一相的相同物种之间。例如,液态水和水蒸气之间的蒸发/凝结。
-
与 Fluent 中的所有相间质量传递模型一样,如果相间物种质量传递过程中涉及气体混合物,它总是被视为“到”相,而液体混合物被视为“从”相。
对于涉及质量传递的物种,两相中的质量分数必须通过求解传输方程来确定。例如,在蒸发/凝结过程中,水液相和水蒸气相的质量分数必须直接从控制方程求解,而不是通过代数方法或物理约束关系来求解。
为了模拟相间物种质量传递,我们同时求解相物种传输方程以及相质量、动量和能量方程。对于相 中物种 的局部质量分数 ,其传输方程为:
其中, 表示第 相, 是系统中的相数。、 和 分别表示第 相的体积分数、密度和速度。 是通过化学反应在相 中生成均质物种 的净速率。 是来自外部源的生成速率,而 是异质反应速率。 表示从相 上的物种 到相 上的物种 的质量转移源。
在实际应用中,相 和相 之间物种质量转移的源项被视为单个项 ,具体取决于质量转移的方向。物种质量转移的体积速率假设为转移物种质量浓度梯度的函数。
其中, 是 相与 相之间的体积质量传递系数, 是界面面积, 是相 中物种 的质量浓度, 是相 中物种 的质量浓度。体积物种质量传递速率的推导在模型方法(第771页)中展示。
为了求解物种质量传递,需要确定 和 的适当值。
14.7.7.1. 模型方法
Ansys Fluent 中使用双阻力模型来模拟相间物种质量传递。在动态平衡状态下,相浓度存在不连续性时,通常无法使用单一整体质量传递系数来模拟多组分物种质量传递。双阻力模型由 Whitman [707](第1098页)首次提出,是一种类似于双阻力热传递模型的通用方法。它考虑了相界面两侧具有不同质量传递系数的独立质量传递过程。
考虑一种物种溶解在 相和 相中,分别具有浓度 和 ,并且存在相界面 。从 相到 相的相间质量传递涉及三个步骤:
-
物种 从 相的主体传递到相界面 。
-
物种 穿过相界面。在 相中被识别为物种 。
-
物种 从界面 传递到 相的主体。
双阻力模型有两个主要假设:
-
物种在相之间的传输速率由界面两侧相内的扩散速率控制。
-
跨越界面的物种传输是瞬时的(零阻力),因此相界面始终处于平衡状态。换句话说,在两相之间的物种传输存在两个“阻力”,它们分别是物种从两个主体相 和 向相界面 的扩散。这种情况在图14.15中以图形方式进行了说明:两阻力模型中的摩尔浓度分布(第772页)。
图14.15:两阻力模型中的摩尔浓度分布

利用方程14.641(第771页),假设 和 分别是第 相和第 相的质量传输系数,相质量交换的体积速率可以表示如下:
从相界面到第 相,
从界面到第阶段,
在相界面动态平衡条件下,总体质量平衡必须得到满足:
在界面处,方程14.650(第773页)所给出的平衡关系同样适用:
其中, 表示质量浓度的平衡比。
从公式 14.642(第 772 页)至公式 14.645(第 772 页),可以确定界面质量浓度:
随后获取界面质量传递速率:
相特定的质量传递系数, 和 ,可以通过《质量传递系数模型》(第776页)中描述的方法之一来确定。也可以在界面的某一侧指定零阻力条件,这相当于无限相特定的质量传递系数。例如,如果 ,其效果是迫使界面浓度与相 中的主体浓度相同。此外,如果已知总体质量传递系数, 可以直接通过常数或用户定义的函数来指定。
14.7.7.2. 平衡模型
平衡模型用于计算公式14.641(第771页)中的平衡比 。平衡模型考虑了两相中的物种处于动态平衡的情况。界面质量传递速率根据两相中平衡物种浓度的关系来确定。
通常在平衡状态下,两相中的物种浓度并不相同。然而,存在一个明确的平衡曲线,将这两种浓度联系起来。对于二元混合物,平衡曲线取决于温度和压力。对于多组分混合物,它还取决于混合物的组成。平衡曲线通常是单调且非线性的,并且通常以相 和 上物种 和 的平衡摩尔分数来表示:
最简单的曲线或关系是准线性的,并假设在平衡状态下,各相物种的摩尔分数成比例:
其中, 是摩尔分数平衡比。这个关系也可以用 、 或 来表示:
其中,、 和 分别代表摩尔浓度、质量浓度和质量分数的平衡比率。这些平衡比率通过以下表达式相互关联:
存在几种著名的界面平衡模型,用于定义或确定各种物理过程的 。Ansys Fluent 提供了三种确定 的方法:
-
拉乌尔定律 -
亨利定律 -
平衡比率
为了量化相 中物种 的浓度,使用了几个不同但相关的变量:
相 中物种 的摩尔浓度
这四个量之间的关系如下:
其中, 表示相 中所有物种的摩尔浓度之和, 表示相 的相密度。
14.7.7.2.1. 拉乌尔定律
在气液系统中,平衡关系最方便地用气相中物种的分压来表示。众所周知,当纯液体与含有其蒸气的气体混合物接触时,动态平衡发生在蒸气物种的分压等于其饱和压力(温度的一个函数)时。拉乌尔定律将这一陈述扩展到与气体接触的理想液体混合物。它指出,相 中蒸气物种的分压 等于其饱和压力 与液体相中摩尔分数 的乘积:
如果气相表现为理想气体,那么道尔顿分压定律给出:
利用公式14.649(第773页)、公式14.652(第774页)以及公式14.653(第774页),拉乌尔定律可以用摩尔分数比的形式重新表述:
平衡比率,。虽然拉乌尔特定律代表了汽液平衡(VLE)方程的最简单形式,但请记住,它的应用范围有限,因为为其推导所做的假设通常是不现实的。最关键的假设是液相为理想溶液。这不太可能成立,除非系统由分子大小和化学性质相似的物种组成,例如苯和甲苯,或正庚烷和正己烷(参见汽液平衡理论(第488页))。
14.7.7.2.2. 亨利定律
拉乌尔特定律仅适用于具有理想液相混合物的相。为了处理气体物种溶解在非理想液相中的情况,亨利定律通过用常数(称为亨利常数)替换方程14.652(第774页)中的饱和压力,提供了一个更普遍的平衡关系。
的单位是压力,并且对于广泛范围的材料,特别是水中溶解的常见气体,其实验值是已知的。它通常对温度有很强的依赖性。上述形式的亨利定律通常在稀薄混合物(摩尔分数小于0.1)和低压(小于20巴)情况下有效[602](第1092页)。
与拉乌尔特定律一样,亨利定律可以与道尔顿定律结合,以平衡比率的形式表达:
其中,平衡比为 。
除了摩尔分数亨利常数 外,摩尔浓度亨利常数 也常被使用:
Fluent提供了三种确定亨利常数的方法:常数法、范特霍夫相关性法以及用户自定义法。在范特霍夫相关性法中,亨利常数是温度的函数:
以及
式中, 表示溶液的焓变,而 则是在参考温度 下的亨利常数。温度的依赖关系如下:
在使用Fluent中的范特霍夫相关性时,您需要指定参考亨利常数的值以及方程14.660(第775页)中定义的温度依赖性。这些是与材料相关的常数,可以在[569](第1090页)中找到。默认情况下,使用氧气的常数。您也可以选择用户定义的常数。
重要提示:无论在Fluent用户界面中选择了什么单位,为了与大多数参考数据表中的表示一致,始终以M/atm的单位表示。Fluent内部会应用适当的单位转换。
14.7.7.2.3. 平衡比
在Raoult定律和Henry定律都不适用的情况下,例如液液萃取或多物种质量转移,Fluent提供了直接指定平衡比的选项。您可以选择以下形式的平衡比:
摩尔浓度平衡比,
摩尔分数平衡比,
质量分数平衡比,
这些指定了从相到相的浓度变量之比,如方程14.649(第773页)和方程14.650(第773页)所定义。您可以指定一个常数值或用户定义的函数。
14.7.7.3. 质量转移系数模型
在Fluent中,总质量转移系数在方程14.647(第772页)中)可以建模为常数或用户定义的函数(UDF)。相质量转移系数(例如,方程14.647(第772页)中的)在相界面两侧定义,可以建模为常数、UDF或相舍伍德数的函数。在相中,舍伍德数表示为:
其中, 表示第 相的扩散系数,而 是一个特征长度(例如气泡或液滴直径)。
相 中的质量传递系数 ,与方程 14.661(第 776 页)中的 类似定义。
舍伍德数(Sherwood number)可以指定为常数,也可以根据几种经验相关性之一来确定。这些方法在以下章节中详细说明:
- 14.7.7.3.1. 常数
- 14.7.7.3.2. 舍伍德数
- 14.7.7.3.3. Ranz-Marshall 模型
- 14.7.7.3.4. Hughmark 模型
- 14.7.7.3.5. Higbie 模型
- 14.7.7.3.6. 用户自定义
14.7.7.3.1. 常数
当建模为常数时,常数体积质量传递系数 由用户指定。
14.7.7.3.2. 舍伍德数
在舍伍德数方法中,用户指定 的常数值,相质量传递系数 根据方程 14.661(第 776 页)计算。
14.7.7.3.3. Ranz-Marshall 模型
Ranz-Marshall 模型采用与 Ranz-Marshall 传热系数模型类似的方法。对于流经球形颗粒的流动,舍伍德数的表达式与传热中的努塞尔数具有相同的形式,其中普朗特数被施密特数所替代:
其中, 表示第 相的Schmidt数,而 则代表相对雷诺数。
其中, 和 分别代表第 相的动态粘度和密度。 表示两相间相对速度的大小。Ranz-Marshall 模型基于稳定流经球形粒子的边界层理论。该模型通常适用于以下条件:
14.7.7.3.4. Hughmark 模型
与 Ranz-Marshall 模型类似,Hughmark 模型 [262](第 1072 页)用于质量传递系数的计算,同样与其热传递系数模型相对应。通过 Hughmark 修正,Ranz-Marshall 模型被扩展至更广泛雷诺数范围:
雷诺数交叉点的选择是为了确保连续性。该模型不应在推荐的施密特数范围之外使用。
14.7.7.3.5. 希格比模型
希格比质量传递系数模型基于希格比的渗透理论[196](第1068页),提供了界面间物种质量传递的质量传递系数。希格比模型采用以下相关性:
其中
液相物种扩散系数
分别是液相的湍流涡流耗散、密度和粘度
14.7.7.3.6. 用户自定义
您还可以使用用户定义的函数来计算质量传递系数。要创建用户定义的函数,请像在其他质量传递情况下一样使用DEFINE_MASS_TRANSFER宏。