除了《用户指南》中“注入类型”部分描述的简单注入类型外，Ansys Fluent还提供了更复杂的喷雾注入类型，用于描述初级破碎现象。对于大多数类型的注入，您需要提供颗粒的初始直径、位置和速度。然而，对于喷雾，有可用的模型来预测液滴大小和速度分布。

所有的雾化模型都使用物理雾化器参数，如喷嘴直径和质量流量，来计算初始液滴大小、速度和位置。

为了实现逼真的雾化器模拟，液滴必须在空间上通过分散角度随机分布，并在释放时间上随机分布。对于Ansys Fluent中的其他类型的注入（非雾化器），所有液滴在时间步开始时沿着固定轨迹释放。雾化器模型使用随机轨迹选择和错位来实现随机分布。关于错位的更多信息可以在《用户指南》的“空间和时间上的颗粒错位”部分找到。

随机轨迹选择是初始液滴方向的随机分散。所有的雾化模型都提供一个初始分散角度，随机轨迹选择在这个角度内选择一个初始方向。这种方法提高了喷雾主导流动结果的准确性。液滴在靠近雾化器的计算单元中分布得更均匀，通过在靠近注入的单元中更平滑地分散阻力，提高了与气相的耦合。能量和物种守恒方程中的源项也在相邻单元中分布得更均匀，提高了求解的收敛性。

Ansys Fluent提供了五种雾化模型，用于从喷嘴类型和液体流量等全局参数预测喷雾特性。您可以将它们选择为注入类型。

在“设置注射属性”对话框中定义相关参数，具体操作请参阅用户指南中的注射类型部分。以下将详细介绍各种雾化器模型。

信息分为以下小节：

• 12.12.1. 直孔雾化器模型
• 12.12.2. 压力旋流雾化器模型
• 12.12.3. 空气辅助/空气辅助雾化器模型
• 12.12.4. 平面扇形雾化器模型
• 12.12.5. 气泡雾化器模型

12.12.1 直孔雾化器模型

直孔雾化器是最常见的类型，也是结构最简单的。然而，其内部喷嘴流动和外部雾化的物理过程却一点也不简单。在Ansys Fluent的直孔雾化器模型中，液体通过喷嘴加速，形成液流，随后破碎成液滴。这个看似简单的过程实际上异常复杂。直孔雾化器可能以三种不同的模式运行：单相、空化和翻转[618]（第1092页）。不同模式之间的转换是突变的，产生截然不同的喷雾效果。内部模式决定了孔口出口处的速度，以及初始液滴大小和液滴扩散角度。每个案例的示意图如图12.17（液体完全充满孔口）、图12.18（进口角后立即形成蒸汽口袋）和图12.19（下游气体围绕喷嘴内的液流）所示。

图12.17 单相喷嘴流动（液体完全充满孔口）

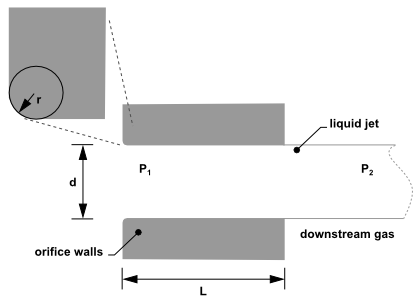
图12.18 空化喷嘴流动（进口角后立即形成蒸汽）

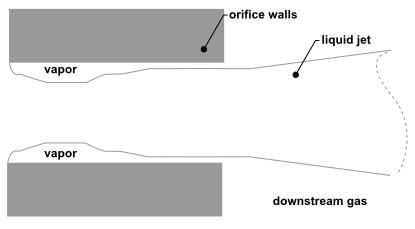
图12.19 翻转喷嘴流动（下游气体围绕喷嘴内的液流）

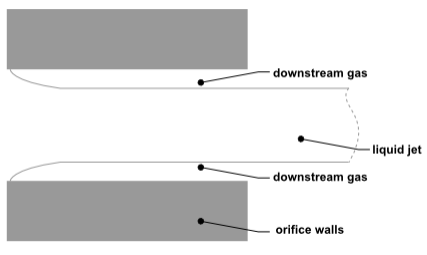
12.12.1.1 内部喷嘴状态

为了准确预测喷雾特性，Ansys Fluent中的平面孔口模型必须识别喷嘴内部流动的正确状态，因为喷嘴状态对喷雾外部特性有着巨大影响。遗憾的是，目前并没有确定喷嘴状态的成熟理论。我们只能依赖从实验数据中获得的经验模型。Ansys Fluent使用多个无量纲参数来确定平面孔口雾化器模型的内部流动状态。以下总结了这些参数及其决策过程。

表12.7列出了控制内部喷嘴流动的参数：内部喷嘴流动的控制参数列表（第543页）。这些参数可以组合形成诸如$r/d$和$L/d$的无量纲特征长度，以及基于液压"头部"的雷诺数${\mathrm{Re}}_h$和空化参数K [482]（第1085页）等无量纲群。

表12.7：内部喷嘴流动的控制参数列表

$$R{e}_h=\frac{d{\rho }_l}{\mu }\sqrt{\frac{2\left(p_1-p_2\right)}{{\rho }_l}}\text{\hspace{1em}(12.353)}$$

$$K=\frac{p_1-p_v}{p_1-p_2}\text{\hspace{1em}(12.354)}$$

如图12.18《空化喷嘴流动（入口角后形成蒸汽口袋）》（第543页）和图12.19《翻转喷嘴流动（下游气体环绕喷嘴内液流）》（第543页）所示，液体流动在喷嘴中往往会收缩。Nurick [482]（第1085页）发现使用收缩系数$\left(C_c\right)$来表示液流横截面积的减小很有帮助。收缩系数定义为收缩液流的截面积与喷嘴总横截面积之比。Ansys Fluent采用了Nurick的收缩系数拟合公式：

$$C_c=\frac{1}{\sqrt{\frac{1}{C_{ct}^2}-\frac{11.4r}{d}}}\text{\hspace{1em}(12.355)}$$

此处，$C_{ct}$ 是一个理论常数，等于0.611，这一数值源自翻转喷嘴的势流分析。

12.12.1.2 流量系数

描述喷嘴性能的另一个重要参数是流量系数 $\left(C_d\right)$。流量系数是指通过喷嘴的质量流量与理论最大质量流量之比：

$$C_d=\frac{{\dot{m}}_{eff}}{A\sqrt{2{\rho }_l\left(p_1-p_2\right)}}\text{\hspace{1em}(12.356)}$$

其中，${\dot{m}}_{eff}$ 表示喷嘴的有效质量流量，定义为

$${\dot{m}}_{eff}=\frac{2\pi \dot{m}}{\Delta \phi }\text{\hspace{1em}(12.357)}$$

在上述表达中，$\dot{m}$ 代表用户界面中设定的质量流量，而 $\Delta \phi$ 则是方位角停止角度与起始角度之间的差值。

$$\Delta \phi ={\phi }_{\text{stop }}-{\phi }_{\text{start }}\text{\hspace{1em}(12.358)}$$

由您输入（参见用户指南中关于普通孔式喷雾器注射的点属性部分）。请注意，您输入的质量流率应适用于相应的起始和终止角度，换言之，即为所模拟扇区的正确质量流率。另请注意，对于 $\Delta \phi$ 为 $2\pi$ 的情况，有效质量流率与界面中的质量流率相同。

空化数（公式 12.354（第 544 页）中的 $K$）是预测空化起始的关键参数。空化的起始被假定发生在以下经验关系给定的值处：

$$K_{\text{incep }}=2{\left(1-\frac{r}{d}\right)}^2-\frac{1000}{R{e}_h}\text{\hspace{1em}(12.359)}$$

同样地，翻转发生的临界值 ( K ) 可以表示为：

$$K_{crit}=1+\frac{1}{\left(1+\frac{L}{4d}\right)\left(1+\frac{2000}{R{e}_h}\right)e^{70r/d}}\text{\hspace{1em}(12.360)}$$

如果 $r/d$ 大于 0.05，则认为翻转不可能发生，此时 $K_{\text{crit}}$ 设为 1.0。

空化数 $K$ 与 $K_{incep}$ 和 $K_{crit}$ 的值进行比较，以确定喷嘴的状态。决策树如图 12.20 所示：空化喷嘴状态决策树（第 545 页）。根据喷嘴的状态，为上述方程选择一个独特的闭合方式。

对于单相喷嘴 $\left(K>K_{\text{incep }},K\ge K_{\text{crit }}\right)$ [370]（第 1078 页），流量系数由...

$$C_d=\frac{1}{\frac{1}{C_{du}}+20\frac{\left(1+2.25L/d\right)}{R{e}_h}}\text{\hspace{1em}(12.361)}$$

其中，$C_{du}$ 是极限流量系数，其定义为

$$C_{du}=0.827-0.0085\frac{L}{d}\text{\hspace{1em}(12.362)}$$

对于空化喷嘴 $\left(K_{\text{crit }}\le K\le K_{\text{incep }}\right)$ [482]（第1085页），流量系数由以下公式确定：

$$C_d=C_c\sqrt{K}\text{\hspace{1em}(12.363)}$$

对于翻转喷嘴 $\left(K<K_{\text{crit }}\right)$ [482]（第1085页），

$$C_d=C_{ct}=0.611\text{\hspace{1em}(12.364)}$$

图12.20：空化喷嘴状态的决策树

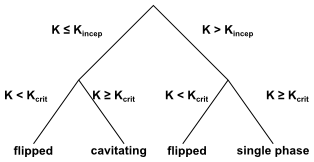
所有喷嘴流动方程都是迭代求解的，同时结合了根据喷嘴状态给出的流量系数关系。喷嘴状态可能会随着上下游压力的变化而改变。一旦确定了喷嘴状态，就会计算出口速度，并确定适当的喷雾角度和初始液滴尺寸分布的相关关系。

12.12.1.3 出口速度

对于单相喷嘴，出口速度 $\left(u\right)$ 的估计来自于质量守恒和出口速度均匀的假设：

$$u=\frac{{\dot{m}}_{eff}}{{\rho }_{l}A}\text{\hspace{1em}(12.365)}$$

对于空化喷嘴，Schmidt和Corradini [581]（第1090页）已经证明，均匀出口速度的假设并不准确。相反，他们推导出了一个在减小面积上具有更高速度的表达式：

$$u=\frac{2C_c{p}_1-p_2+\left(1-2C_c\right)p_v}{C_c\sqrt{2{\rho }_l\left(p_1-p_v\right)}}\text{\hspace{1em}(12.366)}$$

此分析关系式用于Ansys Fluent中的空化喷嘴。对于翻转喷嘴的情况，出口速度根据质量守恒和缩减流面积的值来确定：

$$u=\frac{{\dot{m}}_{eff}}{{\rho }_l{C}_{ct}A}\text{\hspace{1em}(12.367)}$$

12.12.1.4 喷雾角度

喷雾角度 $\left(\theta \right)$ 的相关性源自 Ranz [541]（第1088页）的研究：

$$\frac{\theta }{2}=\{\begin{array}{cc}{\tan }^{-1}\left[\frac{4\pi }{C_A}\sqrt{\frac{{\rho }_g}{{\rho }_l}}\frac{\sqrt{3}}{6}\right]& \text{ single phase, cavitating }\\ 0.01& \text{ flipped }\end{array}\text{\hspace{1em}(12.368)}$$

单相和空化喷嘴的喷雾角度取决于气体和液体密度之比，以及参数$C_A$。对于翻转喷嘴，喷雾角度具有恒定值。

您必须指定的参数$C_A$，被认为是给定喷嘴几何形状下的常数。该值越大，喷雾越窄。Reitz [548]（第1088页）提出了以下关于$C_A$的相关性建议：

$$C_A=3+\frac{L}{3.6d}\text{\hspace{1em}(12.369)}$$

喷雾角度对喷嘴内部的流动状态非常敏感。因此，对于空化喷嘴，您可能希望选择比单相喷嘴更小的 $C_A$ 值。典型值范围从 4.0 到 6.0。翻转喷嘴的喷雾角度是一个较小的任意值，代表喷嘴缺乏任何湍流或初始扰动。

12.12.1.5 液滴直径分布

喷射的基本特性之一是液滴大小的分布。对于雾化器，液滴直径分布与喷嘴状态密切相关。Ansys Fluent 的喷雾模型使用两参数的 Rosin-Rammler 分布，其特征在于最可能的液滴大小和扩展参数。最可能的液滴大小 $d_0$ 在 Ansys Fluent 中从 Sauter 平均直径 $d_{32}$ [351]（第 1077 页）获得。有关 Rosin-Rammler 尺寸分布的更多信息，请参阅用户指南中的使用 Rosin-Rammler 直径分布方法。

对于单相喷嘴流，使用 Wu 等人的相关性 [719]（第 1098 页）来计算 $d_{32}$，并将初始液滴大小与液体射流的估计湍流量相关联。

$$d_{32}=133.0\lambda {\mathrm{We}}^{-0.74}\text{\hspace{1em}(12.370)}$$

其中 $\lambda =d/8$，$\lambda$ 是基于完全发展的湍流管流在射流出口处的径向积分长度尺度，而 We 是韦伯数，定义为

$$We\equiv \frac{{\rho }_l{u}^2\lambda }{\sigma }.\text{\hspace{1em}(12.371)}$$

这里，$\sigma$ 表示液滴表面张力。关于液滴表面张力和韦伯数的更详细讨论，请参见《用户指南》中的“二次破碎模型理论”（第554页）。关于平均颗粒直径的更多信息，请参见《用户指南》中的“当前颗粒的汇总报告”。

对于空化喷嘴，Ansys Fluent 采用对公式 12.370（第547页）的轻微修正。Wu 相关性中使用的初始射流直径 $d$，是根据空化喷嘴出口的有效面积计算的，因此代表了射出的液体射流的有效直径，即 $d_{eff}$。关于空化喷嘴的有效面积的解释，请参见 Schmidt 和 Corradini [581]（第1090页）。

空化喷嘴的长度尺度为 $\lambda =d_{eff}/8$，其中

$$d_{eff}=\sqrt{\frac{4{\dot{m}}_{eff}}{\pi {\rho }_{l}u}}.\text{\hspace{1em}(12.372)}$$

对于翻转喷嘴的情况，初始液滴直径设定为液体射流的直径：

$$d_0=d\sqrt{C_{ct}}\text{\hspace{1em}(12.373)}$$

其中，$d_0$ 定义为最可能直径。

指定液滴尺寸分布所需的第二个参数是扩展参数 $s$。扩展参数的值根据以往的建模经验和实验观察结果进行选择。表12.8：不同喷嘴状态下的扩展参数值（第547页）列出了三种喷嘴状态下的 $s$ 值。扩展参数的值越大，液滴尺寸分布越窄。

表12.8：不同喷嘴状态下的扩展参数值

由于 Wu 等人的相关性提供了 Sauter 平均直径 $d_{32}$，因此这些被转换为最可能直径 $d_0$。Lefebvre [351]（第1077页）给出了 Rosin-Rammler 分布下 Sauter 平均直径与最可能直径之间最一般的关系。简化版本为 $s=3.5$ 时如下：

$$d_0=1.2726d_{32}{\left(1-\frac{1}{S}\right)}^{1/s}\text{\hspace{1em}(12.374)}$$

至此，液滴尺寸、速度和喷射角度已经确定，喷射的初始化完成。

12.12.2 压力旋流雾化器模型

另一种重要的雾化器是压力旋流雾化器，有时被燃气轮机领域称为简单雾化器。这种雾化器通过被称为旋流口的喷嘴将液体加速进入中央旋流室。旋流液体推动旋流室壁并形成中空空气核心。随后，液体以减薄片状从孔口喷出，这种片状不稳定，会破碎成细丝和液滴。压力旋流雾化器在燃气轮机、油炉和直接喷射点燃式汽车发动机中的液体燃料燃烧中被广泛使用。从内部喷射器流动到完全发展的喷雾的转变可以分为三个步骤：膜形成、片状破碎和雾化。这一过程被认为如何发生的草图如图12.21所示：从内部喷射器流动到外部喷雾的理论进展（第548页）。

图12.21：从内部喷射器流动到外部喷雾的理论进展

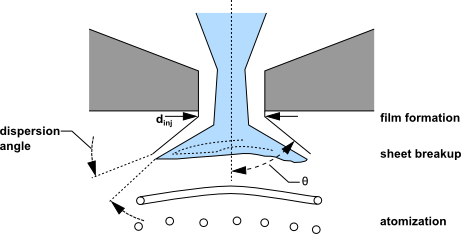
空气与片状之间的相互作用尚未完全理解。普遍认为气动不稳定性导致片状破碎。下面的数学分析假设开尔文-亥姆霍兹波在片状上增长并最终将液体破碎成细丝。然后假设细丝由于静脉曲张不稳定性破碎成液滴。一旦形成液滴，喷雾的演化由阻力、碰撞、聚结和二次破碎决定。

Ansys Fluent中使用的压力旋流雾化器模型称为Schmidt等人[583]（第1090页）的线性不稳定片状雾化（LISA）模型。LISA模型分为两个阶段：

1. 膜形成
2. 薄片分解与雾化

以下将分别描述模型的两个部分。

12.12.2.1. 成膜过程

喷射器内液体的离心运动形成了一个被液膜包围的空气芯。喷射器出口处液膜的厚度$t$与质量流量有关，其关系为：

$${\dot{m}}_{eff}=\pi {\rho }_{l}ut\left(d_{inj}-t\right)\text{\hspace{1em}(12.375)}$$

其中，$d_{inj}$ 为喷嘴出口直径，${\dot{m}}_{eff}$ 为有效质量流率，由公式 12.357（第 544 页）定义。公式 12.375（第 549 页）中的另一个未知量是 $u$，即喷嘴出口处的轴向速度分量。这一量值取决于喷嘴内部的细节，难以从基本原理出发进行计算。因此，采用了 Han 等人 [230]（第 1070 页）的方法。假设总速度与喷嘴压力有关。

$$U=k_v\sqrt{\frac{2\Delta p}{{\rho }_l}}\text{\hspace{1em}(12.376)}$$

其中，$k_v$ 是速度系数。Lefebvre [351]（第1077页）指出，$k_v$ 是喷油器设计和喷射压力的函数。如果将旋流口视为喷嘴，并且假设压力降的主要部分发生在这些口上，那么 $k_v$ 就是流量系数 $\left(C_d\right)$ 的表达式。对于具有锐利入口角和 $L/d$ 比率为4的单相喷嘴，典型的 $C_d$ 值为0.78或更低 [370]（第1078页）。如果喷嘴发生空化，$C_d$ 的值可能低至0.61。因此，0.78可以视为 $k_v$ 的实际上限。其他动量损失的影响通过将 $k_v$ 减少10%至0.7来近似。

$k_v$ 的物理限制要求其从能量守恒的角度小于1，但又要足够大以允许足够的质量流量。空气核心尺寸非负的要求意味着薄膜厚度 $t$ 有以下约束：

$$\pi t\left(d_{inj}-t\right)\le \frac{\pi }{4}{d}_{inj}^2\text{\hspace{1em}(12.377)}$$

结合方程12.375（第549页），我们可以得到轴向速度 ( u ) 的如下约束条件：

$$u\ge \frac{4{\dot{m}}_{eff}}{\pi d_{inj}^2{\rho }_l}\text{\hspace{1em}(12.378)}$$

这可以与公式12.376（第549页）以及 $u=U\cos \theta$ 结合，其中 $\theta$ 是喷雾半角，并假设为已知。由此得到对 $k_v$ 的一个约束条件：

$$k_v\ge \frac{4{\dot{m}}_{eff}}{\pi d_{inj}^2{\rho }_l\cos \theta }\sqrt{\frac{{\rho }_l}{2\Delta p}}\text{\hspace{1em}(12.379)}$$

因此，Fluent 采用以下表达式来计算 $k_v$：

$$k_v=\max \left[0.7,\frac{4{\dot{m}}_{eff}}{\pi d_{inj}^2{\rho }_l\cos \theta }\sqrt{\frac{{\rho }_l}{2\Delta p}}\right]\text{\hspace{1em}(12.380)}$$

假设已知 $\Delta p$，则可利用方程 12.376（第 549 页）求出 $U$。一旦确定了 $U$，便可从中求得 $u$。

$$u=U\cos \theta \text{\hspace{1em}(12.381)}$$

在这一点上，液体薄膜在喷射器出口处的厚度和轴向分量已知。速度的切向分量$\left(w=U\sin \theta \right)$被假定为等于喷嘴出口下游液体薄片的径向速度分量。轴向速度分量被假定为保持不变。

12.12.2.2 薄片破碎与雾化

压力旋流雾化器模型包括了周围气体、液体粘度和表面张力对液体薄片破碎的影响。该模型的理论发展细节由Senecal等人[587]（第1091页）给出，这里仅简要介绍。为了实现更稳健的应用，计算相对液体-气体速度时忽略了气体速度，而是由用户设定。这样可以避免喷射器参数过于依赖通常在注射位置附近未充分解析的气体速度场。

该模型假设一个二维、粘性、不可压缩的液体薄片，厚度为$2h$，以速度$U$穿过静止、无粘性、不可压缩的气体介质。液体和气体的密度分别为${\rho }_l$和${\rho }_g$，液体的粘度为${\mu }_l$。使用了一个与薄片一起移动的坐标系，并考虑了一系列形式为

$$\eta ={\eta }_0{e}^{ikx+\omega t}\text{\hspace{1em}(12.382)}$$

施加在初始稳定运动上的，是公式12.382（第550页）所描述的扰动。这些扰动导致了液体和气体速度与压力的波动。在公式12.382中，${\eta }_0$代表初始波幅，$k=2\pi /\lambda$是波数，而$\omega ={\omega }_r+i{\omega }_i$则是复数增长率。最不稳定的扰动具有最大的${\omega }_r$值，此处记为$\Omega$，并假设其负责液膜的破裂。因此，我们希望得到一个色散关系$\omega =\omega \left(k\right)$，从中可以计算出作为波数函数的最不稳定扰动。

Squire [628]（第1093页）、Li和Tankin [365]（第1078页）以及Hagerty和Shea [225]（第1070页）已经证明，在满足上下界面的边界条件的前提下，控制方程存在两种解，或者说模式。第一种解称为正弦模式，其上下界面的波动是同相的。第二种解称为变异模式，其上下界面的波动相位差为$\pi$弧度。许多作者（例如，Senecal等人[587]（第1091页））已经表明，在低速度和低气体与液体密度比的情况下，正弦模式主导了变异波的增长。此外，可以证明，在高速度流动中，正弦和变异模式变得难以区分。因此，Ansys Fluent中的雾化模型基于液膜上正弦波的增长。

正如Senecal等人[587]（第1091页）所推导的，正弦模式的色散关系为： $${\omega }_r=\frac{1}{\tanh \left(kh\right)+Q}\{-2{\nu }_l{k}^2\tanh \left(kh\right)+\text{\hspace{1em}(12.383)}$$

$$4{\nu }_l{k}^4\tanh (kh)-4{\nu }_l^2{k}^3\ell \tanh (\ell h)-Q{U}^2{k}^2+\frac{\sigma k^3}{{\rho }_l}=0\text{\hspace{1em}(12.384)}$$

其中，$Q={\rho }_g/{\rho }_l$，${\ell }^2=k^2+\omega /v_l$。

当韦伯数超过临界值$W{e}_g=27/16$（基于液体速度、气体密度和薄片半厚度）时，增长最快的波是短波。对于$W{e}_g<27/16$，波长远大于薄片厚度。现代高压燃油喷射系统的速度足够高，确保薄片的韦伯数远超过这一临界值。

利用典型数值进行的数量级分析表明，与方程12.384（第550页）中的其他项相比，粘度的二阶项可以忽略不计。基于这一假设，方程12.384（第550页）简化为

$${\omega }_r=\frac{1}{\tanh \left(kh\right)+Q}\{-2v_l{k}^2\tanh \left(kh\right)+\text{\hspace{1em}(12.385)}$$

$$\sqrt{4v_l^2{k}^4{\tanh }^2\left(kh\right)-Q^2{U}^2{k}^2-\left[\tanh \left(kh\right)+Q\right]\left[-Q{U}^2{k}^2+\frac{\sigma k^3}{{\rho }_l}\right]}\}\text{\hspace{1em}(12.386)}$$

对于波长远大于薄片厚度的情况，采用了Dombrowski和Johns [145]（第1065页）提出的薄片解体机制。对于长波，一旦不稳定的波达到临界振幅，就假定薄片破裂过程中会形成小滴。如果在破裂时表面扰动达到了${\eta }_b$值，则可以评估出一个破裂时间$\tau$：

$${\eta }_b={\eta }_0{e}^{\Omega \tau }\Rightarrow \frac{1}{\Omega }\ln \left(\frac{{\eta }_b}{{\eta }_0}\right)\text{\hspace{1em}(12.387)}$$

其中，$\Omega$，即最大增长率，是通过数值最大化方程12.386（第551页）作为$k$的函数来找到的。最大值的寻找采用了一种二分搜索法，该方法通过检查导数的符号来进行。当薄片断裂时，将在给定长度处形成韧带。

$$L_b=U\tau =\frac{U}{\Omega }\ln \left(\frac{{\eta }_b}{{\eta }_0}\right)\text{\hspace{1em}(12.388)}$$

其中，量 $\ln \left({\eta }_b/{\eta }_o\right)$ 是一个经验性的膜常数，需要您指定。默认值 12 是 Weber [695]（第 1097 页）根据液体射流理论推导出的。Dombrowani 和 Hooper [144]（第 1065 页）表明，对于从 2 到 200 的 Weber 数范围，膜常数值 12 与实验测得的膜破碎长度吻合良好。

在破碎点形成的丝状物的直径可以通过质量平衡计算得出。如果假设丝状物每波长两次从膜中撕裂形成，那么得到的直径为

$$d_L=\sqrt{\frac{8h}{K_s}}\text{\hspace{1em}(12.389)}$$

其中，$K_s$ 是对应于最大增长率 $\Omega$ 的波数。丝状直径取决于片层厚度，而片层厚度又是破碎长度的函数。从破碎长度和从中心线到雾化器出口处片层中线处的径向距离 $r_0$ 来计算膜厚：

$$h_{end}=\frac{r_0{h}_0}{r_0+L_b\sin \left(\frac{\theta }{2}\right)}\text{\hspace{1em}(12.390)}$$

对于波长较短的情况，即波长远小于板厚时，该机制并不适用。在短波情况下，我们假定液丝直径与导致板材破裂的波长呈线性正比关系。

$$d_L=\frac{2\pi C_L}{K_s}\text{\hspace{1em}(12.391)}$$

其中，$C_L$，即液丝常数，默认值为0.5。

无论是在长波还是短波情况下，从液丝破裂成液滴的过程都被假设

遵循韦伯[695]（第1097页）关于毛细不稳定性的分析。

$$d_0=1.88d_L{\left(1+30h\right)}^{1/6}\text{\hspace{1em}(12.392)}$$

在此，$Oh$ 表示 Ohnesorge 数，它是雷诺数和韦伯数的组合（有关 Oh 的更多详细信息，请参阅第 560 页的射流稳定性分析）。一旦从公式 12.392（第 552 页）确定了 $d_0$，就假定这个液滴直径是 Rosin-Rammler 分布中最可能的液滴大小，其扩展参数为 3.5，默认分散角度为 $6^{\circ }$（可以在用户界面中修改）。扩展参数和分散角度的选择基于以往的建模经验 [582]（第 1090 页）。需要注意的是，在使用此模型时，必须由您指定喷雾锥角。

12.12.3 空气喷射/空气辅助雾化器模型

为了加速从雾化器喷出的液体薄片的破碎，通常会通过雾化器引导额外的空气流。液体通过喷嘴形成薄片，然后空气被导向薄片以促进雾化。根据空气的量及其速度，这一技术被称为空气辅助雾化或空气喷射雾化。在薄片之后添加外部空气流会产生比没有空气时更小的液滴。尽管这种增强性能的确切机制尚未完全理解，但人们认为辅助空气可能会加速薄片的不稳定性。空气还可能有助于分散液滴，防止它们之间的碰撞。空气辅助雾化在许多与压力旋流雾化相同的应用中使用，特别需要精细雾化时。

Ansys Fluent的空气喷射雾化模型是压力旋流模型的一种变体。它们之间的一个重要区别在于，在空气喷射雾化器模型中，薄片厚度是直接设定的。这一输入是必要的，因为空气喷射雾化器采用了多种薄片形成机制。因此，空气喷射雾化器模型不包含压力旋流雾化器模型中的薄片形成方程（公式12.375（第549页）至公式12.381（第549页））。您还需要指定薄片和空气产生的最大相对速度。虽然这个量可以计算，但指定一个值可以免去精细解析雾化器内部流动的必要，这在模拟大区域时非常方便，因为雾化器相比之下非常小。

另一个不同之处在于，空气喷射雾化器模型假设薄片破碎总是由短波引起的。这一假设是由于空气喷射雾化器中常见的较大薄片厚度所致。因此，液滴直径被假定为与薄片上最快增长波的波长成线性比例，并根据公式12.391（第551页）计算得出。

其他输入与压力旋流模型相似——您必须提供质量流量和喷雾角度。在空气喷射雾化器的情况下，角度是指薄片离开喷嘴末端的初始轨迹。此外，还需要指定雾化器出口处薄片的内径和外径，以及分散角度，其默认值为6（可在用户界面中修改）。

由于空气冲击式喷嘴模型不包括内部气体流动，您必须在Ansys Fluent模拟中将围绕喷嘴的气流创建为边界条件。这些气流是普通的连续相流动，不需要特殊处理。

12.12.4 平板扇形喷嘴模型

平板扇形喷嘴与压力旋流喷嘴非常相似，但它产生的是平板而非旋流。液体从宽而薄的孔口流出，形成一个平板状的液膜，随后破碎成液滴。主要的雾化过程被认为与压力旋流喷嘴相似。一些研究人员认为，由于射流的冲击作用，平板扇形雾化与平板状液膜的雾化非常相似。平板扇形模型可以为此应用提供双重服务。

平板扇形喷嘴仅适用于3D模型。图12.22显示了从上方和侧面观察的三维平板扇形（第553页）。该模型假设扇形源自一个虚拟原点。您需要提供这个原点的位置，即标记扇形两侧的线的交点，以及扇形起源的圆弧中心点的位置。Ansys Fluent将找到从原点到中心点的矢量，以确定喷射方向。您还需要提供扇形圆弧的半角、孔口的宽度（在法线方向上）以及液体的质量流量，以使用平板扇形喷嘴模型。

图12.22：从上方和侧面观察的平板扇形

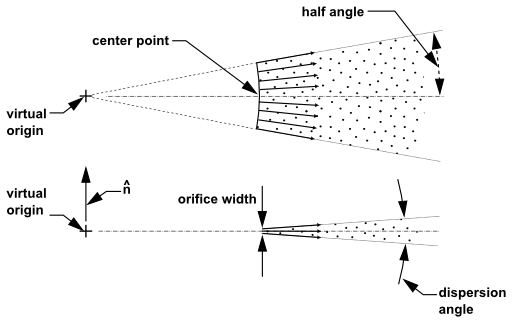
扁平扇形液膜的破碎过程与压力旋流式雾化器中液膜的破碎过程非常相似。液膜先破碎成细丝，然后形成单个的液滴。唯一的区别在于，对于短波而言，扁平扇形液膜被假设在半波长间隔处形成细丝。因此，短波对应的细丝直径可以通过以下方式给出。

$$d_L=\sqrt{\frac{16h}{K_s}}\text{\hspace{1em}(12.393)}$$

在这种情况下，方程12.393（第553页）中的$d_L$被视为最可能的直径，具有3.5的Rosin-Rammler分布参数和6度的默认分散角度。此角度可在设置喷射属性对话框中进行设置。在所有其他方面，扁平扇形雾化器模型类似于压力旋流雾化器的片状破碎部分。

12.12.5 起泡雾化器模型

起泡雾化是指注入含有过热（相对于下游条件）液体或推进剂的液体。当挥发性液体从喷嘴出口时，它会迅速改变相态。这种相变迅速将流体分解成具有宽分散角度的小液滴。该模型也适用于排放非常热液体的情况。

由于起泡的物理机制尚未被充分理解，该模型必须依赖于粗略的经验拟合。Reitz和Bracco [548]（第1088页）的摄影作品提供了一些见解。这些照片显示了喷雾中密集的液体核心，周围被一层较小的液滴所包围。

液滴的初始速度是根据质量守恒计算的，假设喷射流具有的横截面积是喷嘴面积的$C_{ct}$倍，其中$C_{ct}$是一个固定常数，等于0.611，如方程12.355（第544页）和方程12.364（第545页）所指定。

$$u=\frac{{\dot{m}}_{eff}}{{\rho }_l{C}_{ct}A}\text{\hspace{1em}(12.394)}$$

最大液滴直径设定为喷射出口的有效直径：

$$d_{\max }=d\sqrt{C_{ct}}\text{\hspace{1em}(12.395)}$$

随后，液滴尺寸从具有4.0扩展参数的Rosin-Rammler分布中进行采样。（关于Rosin-Rammler分布的详细信息，请参阅用户指南中的“使用Rosin-Rammler直径分布方法”部分。）最可能的液滴大小取决于液滴随机轨迹与喷射方向之间的角度$\theta$。

$$d_0=d_{\max }{e}^{-{\left(\theta /{\theta }_s\right)}^2}\text{\hspace{1em}(12.396)}$$

散射角乘数，${\Theta }_s$，根据质量$x$和给定的散射常数$C_{eff}$的指定值计算得出：

$$x=\frac{{\dot{m}}_{\text{vapor }}}{\left({\dot{m}}_{\text{vapor }}+{\dot{m}}_{\text{liquid }}\right)}\text{\hspace{1em}(12.397)}$$

$$\Theta s=\frac{x}{C_{eff}}\text{\hspace{1em}(12.398)}$$

这种技术能产生一种喷雾，其中心核心部分为大液滴，而周围则环绕着较小液滴的遮蔽层。液滴的初始温度设定为饱和温度的0.99倍，使得液滴温度接近沸腾点。为了完善模型，计算中还必须纳入闪蒸蒸汽。这部分蒸汽属于连续相，而非离散相模型的一部分。在为连续相设定边界条件时，您必须在喷射点创建一个入口。当选择发泡雾化器模型时，除了指定喷射器的位置和方向外，您还需要提供喷嘴直径、质量流率、混合品质、易挥发物质的饱和温度、喷雾半角以及分散常数。