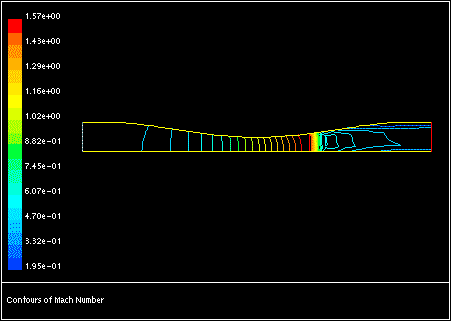
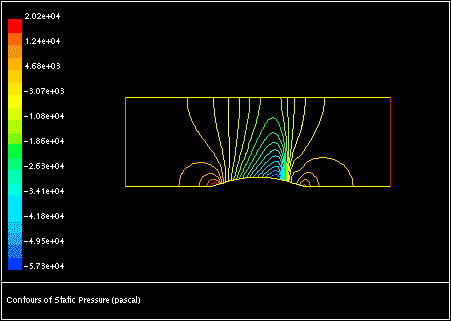
在高速度气流和/或在压力变化较大的气流传动中会遇到可压缩性效应。当流动速度接近或超过气体音速时，或者当系统中的压力变化 $(Δ p / p)$ 很大时，气体密度随压力的变化对流动速度、压力和温度有显著影响。可压缩流产生一组独特的流动物理现象，对于这部分描述的特殊输入要求和求解技术，你必须有所了解。图1.7：收敛-发散喷嘴中的跨音速流动（第13页）和图1.8：二维通道中隆起上方的马赫0.675流动（第13页）展示了使用Fluent计算的可压缩流例子。

图1.7 收敛-扩散喷管中的跨音速流

图1.8 二维通道中凸起物上的马赫数0.675流场

有关在Fluent中设置可压缩流的更多信息，请参阅用户指南中的“可压缩流”部分。

1.6.1 何时使用可压缩流动模型

可压缩流动可通过马赫数的大小来表征：

$M \equiv u / c (1.26)$

式中 $c$ 为气体中的声速：

$c = γ RT (1.27)$

其中 $γ$ 是比热容比，即 $(c_{p} / c_{v})$ 。

式1.27适用于理想气体。在一般情况下，对于真实流体，声速根据等熵压缩率来定义：

$c = 1/ (\frac{\partial ρ}{\partial p})_{s} (1.28)$

其中， $ρ$ 为流体的密度， $p$ 为压力，下标 $s$ 为在恒定熵条件下密度 $ρ$ 对压力 $p$ 的偏导数。

当马赫数低于1.0时，流动被定义为亚音速。在马赫数远低于1.0（大约M < 0.1）的情况下，可压缩性效应可以忽略不计，气体密度的压力变化在流动中可以安全地忽略。随着马赫数接近1.0（这一区域被称为跨音速流动区），可压缩性效应变得重要。当马赫数超过1.0时，流动称为超音速，流场中可能包含激波和膨胀波等现象，这些都会显著影响流动模式。Fluent提供了广泛的适用于亚音速、跨音速和超音速的可压缩流体模拟能力。

1.6.2. 可压缩流体的物理特性

可压缩流动通常以总压 $p_{0}$ 和总温 $T_{0}$ 为特征。对于理想气体，这些物理量可以通过以下关系与静压和温度相关联：

$\frac{p _{0}}{p} = exp (\frac{\int _{T}^{T_{0}} \frac{C _{p}}{T} d T}{R}) (1.29)$

当 $C_{p}$ 为常数时，式1.29可简化为：

$\frac{p _{0}}{p} = (1 + \frac{γ - 1}{2} M^{2})^{γ / (γ - 1)} (1.30)$

$\frac{T _{0}}{T} = 1 + \frac{γ - 1}{2} M^{2} (1.31)$

这些关系描述了在等熵条件下，随着速度（马赫数）变化时流体静压和温度的变化情况。例如，给定从入口到出口（总压到静压）的压力比，可以使用式1.30来估算在一维等熵流动中存在的出口马赫数。对于空气，式1.30预测在等熵压力比 $p / p_{0}$ 为0.5283时会出现临界流（马赫数为1.0）。这种临界流条件将在最小流通面积处（如喷管喉部）建立。在随后的面积扩张中，流动可能加速至超音速状态，压力继续下降；或者恢复到亚音速流动条件，减速并伴随着压力上升。如果超音速流动遇到外部施加的压力增加，将会发生激波现象，激波前后压力突然升高且速度骤减。

1.6.2.1 可压缩流动基本方程

可压缩流动由Fluent标准连续性方程和动量方程描述，并且无需启用任何特殊物理模型（除了以下详细说明的密度可压缩处理）。Fluent求解的能量方程正确地考虑了流速与静温度之间的耦合关系，因此在求解可压缩流动时应当启用。此外，如果使用压力基求解器，应启用方程5.1中的粘性耗散项，这些项在高马赫数流中需要考虑。

1.6.2.2 气体定律的可压缩形式

对于可压缩流，理想气体定律表示为：

$ρ = \frac{p _{o p} + p}{\frac{R}{M _{w}} T} (1.32)$

其中， $p_{o p}$ 为在Operating Conditons对话框中定义的操作压力， $p$ 为相对于操作压力的局部静压， $R$ 为通用气体常数， $M_{w}$ 为分子量。温度 $T$ 通过能量方程计算得出。

某些可压缩流问题涉及的流体并不表现为理想气体。例如，在极高压力条件下的流动通常不能用理想气体假设来准确模拟。这种情况应使用《用户指南》中描述的真实气体模型（Real Gas Models）来进行模拟。