许多重要工程流体涉及旋流或旋转,而Fluent具备出色模拟此类流动的能力。旋流在燃烧过程中十分常见,通过在燃烧器和燃烧室内引入旋流,能延长停留时间并稳定流动模式。此外,旋转流动还广泛应用于涡轮机械、混合罐及其他多种场合。
开始分析旋转或旋流时,将问题归类为以下五种流动类型之一至关重要:
- 带有旋流或旋转的轴对称流动
- 完全三维的旋流或旋转流动
- 需要运动参考系的流动
- 需要多个运动参考系或混合平面的流动
- 需要滑移网格的流动
本节介绍了前两类模型的建模和求解过程。其余三类涉及“移动区域”的内容将在《带运动参考系的流动》中讨论。
1.5.1 旋流与旋转流动
1.5.1.1 带有旋流或旋转的轴对称流动
用户可以解决涉及预测周向或旋流速度的二维轴对称问题。根据轴对称的假设,流动中不存在周向梯度,但可能存在非零的周向速度。图1.3展示了一个涉及旋流或旋转的轴对称流动示例:腔体内的旋转流动;而图1.4(第10页)则展示了燃气燃烧器中的旋流情况。
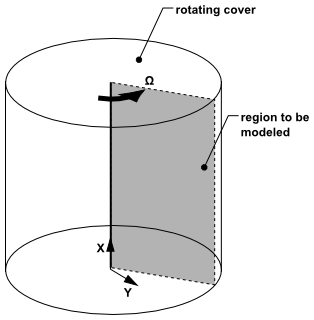
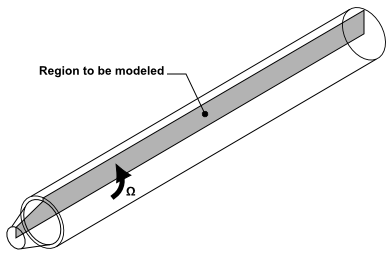
问题可能在几何形状和流动条件上呈现对称性,但仍可能包含旋流或旋转。在这种情况下,可以在二维空间中模拟流动(即解决轴对称问题)并预测周向(或旋流)速度。需要注意的是,尽管轴对称假设意味着流动中不存在周向梯度,但仍可能存在非零的旋流速度。
1.5.1.1.1 旋流速度的动量守恒方程
对于二维旋流流动,切向动量方程可以写为
其中, 为轴向坐标, 为径向坐标, 为轴向速度, 为径向速度,而 为旋流速度。
1.5.1.2 三维旋流流动
在几何形状变化或周向流动梯度存在的情况下,预测旋流流动需采用三维模型。若打算构建包含旋流或旋转的3D Fluent模型,应熟悉相关的设置限制(详见《Fluent用户指南》中的坐标系限制部分)。此外,在建模初期考虑将问题简化为等效的轴对称问题可能更为有利。鉴于旋流流动的高度复杂性,通过二维研究快速评估不同模拟和设计方案的影响具有重要意义。
重要提示:对于涉及旋流或旋转的3D问题,在设置问题时无需特殊输入,也不需要特殊的求解步骤。但请注意,您可能希望使用柱坐标系来定义速度入口边界条件输入,如用户指南中“定义速度”部分所述。此外,在求解过程中逐步增加旋转速度(作为壁面或入口边界条件设定)可能会对稳定性有所帮助。更多详情,请参阅用户指南中的“通过逐渐增加旋转或旋流速度提高解的稳定性”章节。
1.5.1.3 涉及运动参考系的流动
若流场涉及穿过流体的旋转边界(例如,叶轮叶片或带有凹槽或缺口的表面),则需采用移动参考系来建模。此类应用在“移动参考系中的流动”一节中有详细描述。若存在多个旋转边界(例如,串联的多个叶轮),可使用多参考系模型(详见“多重参考系模型”一节,第24页)或混合面模型(详见“混合面模型”一节)。
1.5.2 旋流与旋转流动的物理学
在旋流中,角动量守恒( 或 常数)倾向于形成自由涡流,其中周向速度 随着半径 的减小而急剧增加(最终在 附近因粘性力开始占主导地位而衰减至零)。龙卷风就是自由涡流的一个例子。图1.5:自由涡流中的典型周向速度径向分布(第11页)展示了典型自由涡流中 的径向分布情况。

可以证明,对于一个理想的自由涡流,由圆周运动产生的离心力与径向压力梯度处于平衡状态:
随着非理想涡旋中角动量分布的演变,这种径向压力梯度的形式也会发生变化,从而驱动径向和轴向流以响应由此产生的非常不均匀的压力。因此,当你在Fluent模型中计算漩涡分布时,你也会注意到静压分布的变化以及相应的轴向和径向流速变化。正是漩涡与压力场之间的高度耦合,使得旋流建模变得复杂。
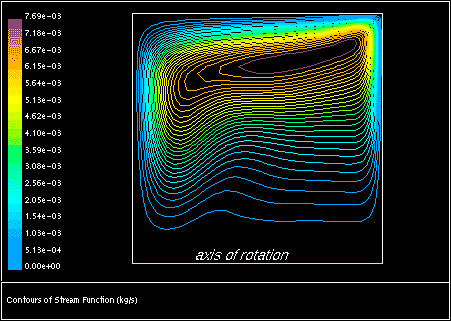
在由壁面旋转驱动的流动中,壁面的运动倾向于给流体施加强迫涡流运动,其中 或 为常数。这类流动的一个重要特征是具有高角动量(例如,靠近壁面的流动)的流体趋向于径向向外抛出(参见图1.6:腔体旋转流动的势函数等值线(第12页),使用图1.3:腔体旋转流动的几何形状(第10页))。这通常被称为“径向泵送”,因为旋转壁面正在将流体径向向外泵送。