流体-流体曳力校正

曳力校正描述了浓度如何修正多颗粒系统中的单颗粒曳力系数。

Richardson Zaki 曳力校正

此曳力校正法用于应用范围广泛的球形颗粒。 根据此模型，浓度增加会对球形颗粒造成阻碍。 与仅通过降低两相混合物对颗粒的浮力相比，终端速度会降低得更快。

此模型还可以涵盖小到足以保持其球体形状的液滴，以及内部粘度高到足以可忽略内部循环的液滴。 此模型还适用于表面污染导致表面不动的气泡，例如普通自来水中的气泡。

根据原始指定，用于球形颗粒的终端速度校正的 Richardson Zaki 模型 [534] 如下：

$$\frac{V}{V_{\infty }}={\alpha }_c^n$$

(1978)

范围	n 对应小管	n 对应大管
${\text{Re}}_{\infty }<0.2$	$4.65$	$4.65$
$0.2<{\text{Re}}_{\infty }<1$	$(4.35+17.5\frac{d}{D})R{e}_{\infty }^{-0.03}$	$4.35R{e}_{\infty }^{-0.03}$
$1<{\text{Re}}_{\infty }<200$	$(4.45+18\frac{d}{D})R{e}_{\infty }^{-0.1}$	$4.45R{e}_{\infty }^{-0.1}$
$200<{\text{Re}}_{\infty }<500$	$4.45R{e}_{\infty }^{-0.1}$	$4.45R{e}_{\infty }^{-0.1}$
${\text{Re}}_{\infty }>500$	$2.39$	$2.39$

$n$ 为 Richardson Zaki 指数， $D$ 为管直径， $d$ 为颗粒直径。

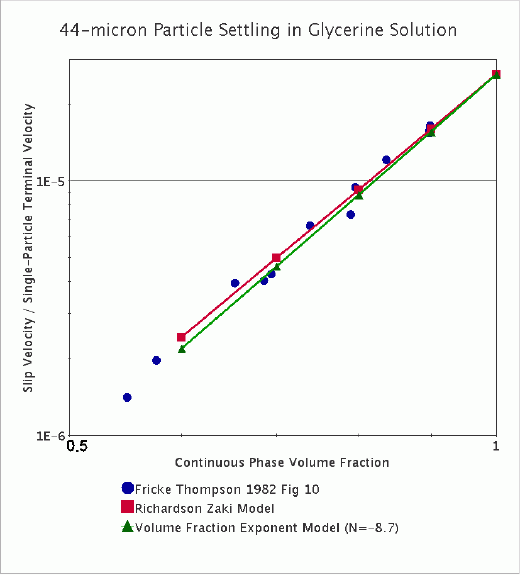
下面两张图说明了 Richardson Zaki 方法的广泛适用性。 第一张图显示在 Stokesian 颗粒沉降测试 ( ${\text{Re}}_{\infty }<0.2$ ) 中根据 Fricke 和 Thompson 的 [461] 中的数据计算出的终端速度校正因子。 甘油-水混合物中的 44 微米树脂颗粒悬浮液的沉降速率受颗粒浓度影响。 通过 Richardson Zaki 方法或通过体积分数指数方法并使用指数 $n_D$ =-8.7 均可准确预测该速率。

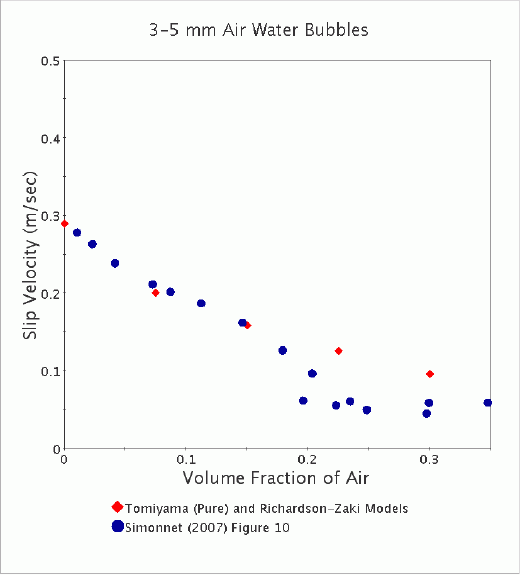
第二张图显示在 ${\text{Re}}_{\infty }>500$ 条件下 3-5 mm 气泡在水中上升时，根据 Simonnet 的 [545] 中的数据得到的终端速度。 尽管气泡在此尺寸范围内为椭圆形，但是一致性较高。

通过以下操作修改原始 Richardson Zaki 模型以用于计算：

• 省略小管项，因为此项会在各雷诺数范围之间产生不可接受的不连续性
• 使用 min() 和 max() 函数确保各雷诺数范围之间完全连续
• 允许更新或调整原始标定常数。
• 防止曳力校正级别随着连续相体积分数渐变为零而变得过高或过低。 为离散相体积分数的总和设置最大填充 ${\alpha }_{d,max}$ ，使得曳力校正的强度在此浓度范围外不会进一步变化。

  $$f_V=max({\alpha }_c,{1-\alpha }_{d,max})$$

  (1979)

  $$n=max\{\begin{array}{c}min\{\begin{array}{c}A\\ min(BR{e}_{\infty }^{n_1},CR{e}_{\infty }^{n_2})\end{array}\\ D\end{array}$$

  (1980)

  $$R{e}_{\infty }=\frac{Re}{f_V}$$

  (1981)

  $$f_D=\{\begin{array}{c}\begin{array}{c}\frac{{\alpha }_c}{f_V^2}\text{Spherical Particle Interfacial area}\end{array}\\ \begin{array}{c}\frac{1}{f_V^2}\text{Symmetric Interfacial area }\end{array}\end{array}$$

  (1982)

单颗粒雷诺数 ${\text{Re}}_{\infty }$ 应用于单颗粒拖曳法以及 Richardson Zaki 校正本身。 对于曳力系数为雷诺数的强函数的流态，这是正确再现终端速度所必需的。

无论使用这两个交界面面积模型中的哪个，此实现都会提供相同的曳力系数和终端速度结果，至少高达最大填充点。

默认标定适用于球形颗粒，但可对其进行修改：

$A$	$B$	$C$	$D$	$n_1$	$n_2$	${\alpha }_{d,max}$
4.65	4.35	4.45	2.39	-0.03	-0.1	0.66

Lockett Kirkpatrick 曳力校正

Lockett 和 Kirkpatrick 的 [508] 调查了气泡浓度对水中的 5-mm 气泡产生的影响。 他们使用向下流体获得了空隙率高达 66% 的稳定气泡流。 他们将 Richardson Zaki 模型应用于球形颗粒以获取水中的 5-mm 气泡的终端速度数据。 该模型假设曳力系数和曳力校正均位于与雷诺数无关的范围内。 在此范围内，即 $\text{Re}$ > 500，Richardson Zaki 指数 n 为 2.39。 他们发现，应用进一步的经验因子以将气泡变形考虑在内，可以获得更好的数据拟合。

在更下方的图中，将 Lockett Kirkpatrick 方法与 Simonnet 等人的 [545] 方法进行比较来预测 7-10 mm 气泡的 Simonnet 终端速度数据。 空隙率不超过 15% 时，一致性较高，超过之后，Simonnet 发现 5-mm 气泡的 Lockett Kirkpatrick 数据未表现出密集特性。

原始 Lockett Kirkpatrick 模型如下：

$$\frac{V}{V_{\infty }}={\alpha }_c^{2.39}[1+2.55{\left(1-{\alpha }_c\right)}^3]$$

(1983)

修改此 Lockett Kirkpatrick 模型以用于计算的方法为，通过最大填充标准 ${\alpha }_{d,max}$ 来限制 ${\alpha }_c$ 的极值的校正。 ${\alpha }_{d,max}$ 的默认值为 0.66。

$$\widetilde{{\alpha }_c}=max({\alpha }_c,{1-\alpha }_{d,max})$$

(1984)

$$f_V={\left({\tilde{\alpha }}_c\right)}^{2.39}[1+2.55{\left(1-{\tilde{\alpha }}_c\right)}^3]$$

(1985)

$$f_D=\{\begin{array}{c}\begin{array}{c}\frac{\alpha }{f_V^2}\text{Spherical Particle Interfacial area}\end{array}\\ \begin{array}{c}\frac{1}{f_V^2}\text{Symmetric Interfacial area}\end{array}\end{array}$$

(1986)

无论使用何种交界面面积模型，此方法都会提供相同的曳力系数和终端速度结果，至少高达最大填充点。

Simonnet 曳力校正

这是 7-10 mm 尺寸范围（Eotvos 数 6.6-13.4）和 0-30% 空隙率范围内空气/气泡的曳力校正。 在 0-15% 范围内，会发生阻碍效应；在 15-30% 范围内，会发生密集效应。

Simonnet 等人的 [545] 中极其谨慎地使用均匀尺寸分布测量了终端速度。 他们针对 7-10 mm 范围内的曳力校正因子的建议模型如下：

$$\frac{C_D}{C_{D\infty }}={\alpha }_c{[{\alpha }_c^{25}+{\left(4.8\frac{1-{\alpha }_c}{{\alpha }_c}\right)}^{25}]}^{-2/25}$$

(1987)

但是，他们还发现，气泡较小 (2-6 mm) 时，仅出现阻碍行为。

下面针对 Simonnet 自己的空气-水中 7-10 mm 气泡 [545] 的数据，比较了使用 Simonnet 的阻碍/密集法以及 Lockett 和 Kirkpatrick 的 [508] 的仅阻碍法计算的终端速度。 当密集行为出现时，这两种方法都与空隙率不超过 15% 的数据完美匹配。

随着连续相体积分数渐变为零，通过使校正线性平滑地接近零来改写 Simonnet 模型以用于计算，便可在 Simonnet 数据的空隙率范围之外安全使用该模型。

$$f_D=s{f}_{D1}+(1-s)f_{D2}$$

(1988)

$$f_{D1}={\alpha }_c{[{\alpha }_c^{25}+{\left(4.8\frac{1-{\alpha }_c}{{\alpha }_c}\right)}^{25}]}^{-2/25}$$

(1989)

$$f_{D2}={0.25\alpha }_c$$

(1990)

$$s=0.5\{1+\tanh \left(\frac{{\alpha }_c-0.7058}{0.05}\right)\}$$

(1991)

在 Simonnet 曳力校正模型的 0-30% 空隙率适用范围内使用它时，球形颗粒交界面面积密度和对称交界面面积密度模型将得出相同的曳力系数和终端速度结果。

体积分数指数曳力校正

此曳力校正模型假设曳力校正因子的形式如下：

$$f_D={\alpha }_c^{n_D}$$

(1992)

其中， $n_D$ 为某一常数幂次。

此方法通过涵盖实际相关的多种流态，补充了其他曳力校正法，例如：

• Stokesian 曳力条件下的小球形颗粒沉降。
• 湍流尾流曳力条件下的大球形颗粒。
• 搅动湍流流态下密集的球帽形气泡。

流态	参考	n	$n_D$ （球形颗粒交界面面积）	$n_D$ （对称交界面面积）
小球形颗粒 ${\text{Re}}_{\infty }<0.2$	[534]	+4.65	-8.3	-9.3
大球形 颗粒 ${\text{Re}}_{\infty }>500$	[534]	+2.39	-3.78	-4.78
搅动湍流流态下的球帽形气泡	[481]	-0.5	+2	+1

这三种流态中的第一种已显示在 Richardson Zaki 部分中关于 Stokesian 条件下的稀释颗粒沉降的图中。 沉降速度是浓度的强函数。 使用曳力校正指数 $n_D=-8.7$ 相当于使用 Fricke 和 Thompson 建议的速度校正指数 $n=4.85$ ，可获得与其自己数据 [461] 的完美拟合。

搅动湍流流态中的曳力校正法是根据 Ishii 和 Zuber 等人的 [481] 获取的，适用于鼓泡塔中的大球帽形气泡。 在此类柱中，气泡尺寸取决于聚结和破碎，并且与入口处的进入气泡的初始尺寸无关。

Ishii 和 Zuber 提出此流态中的气泡的特征为韦伯数为 8，曳力系数为 8/3。 这两个数据都是根据其漂移通量模型速度定义的。 这会导致模型仅预测密集行为。 随着连续相体积分数的幂次分别增加到 -1/2、-3/4 和 +2，气泡等效直径、终端速度和曳力系数都会变化。

Ishii 和 Zuber 发现此模型低估了稀释亚硫酸钠溶液中气泡的表观速度的 Akita 和 Yoshida 数据（在 Ishii 和 Zuber 的 [481] 的图 16 中表示）。 但是，它确实显示了表观速度相对于气泡浓度的正确趋势，并且是最大直径为 60 cm 的气泡柱中的数据的合理近似。

在下面重现的验证计算中，当空隙率从 1% 增加到 30% 时，等效气泡直径从 11 mm 变为 13 mm。 终端速度从 23 cm/s 增加到 30 cm/s，与根据相关指数得到的预期相同。

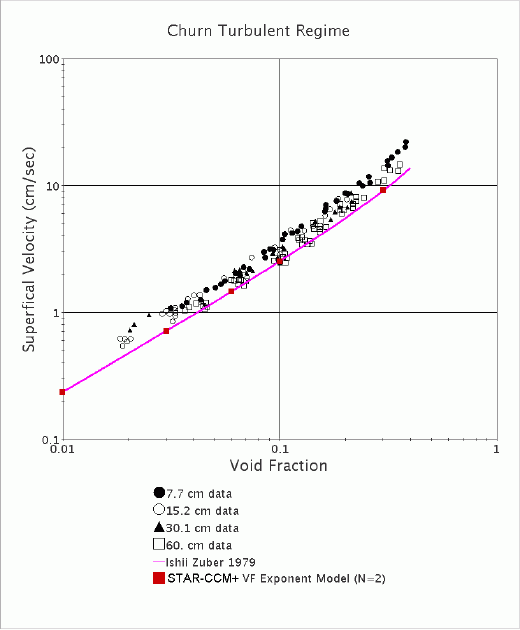
改写恒定指数法以用于计算的方法为，限制 ${\alpha }_c$ 的极值校正。 这是通过最大填充标准 ${\alpha }_{d,max}$ （默认值为 0.66）完成的：

$${\tilde{\alpha }}_c=max({\alpha }_c,{1-\alpha }_{d,max})$$

(1993)

$$f_D={\left({\tilde{\alpha }}_c\right)}^{n_D}$$

(1994)

$$f_V=\{\begin{array}{c}\begin{array}{c}\sqrt{\frac{\alpha }{f_D}}\text{Spherical Particle Interfacial Area}\end{array}\\ \begin{array}{c}\sqrt{\frac{1}{f_D}}\text{Symmetric Interfacial Area }\end{array}\end{array}$$

(1995)

此速度校正因子 $f_V$ 用于正确计算单颗粒终端速度，其中曳力系数取决于雷诺数。 但是，如果单颗粒曳力系数不是雷诺数的函数，则此雷诺数调整没有多少意义。 例如，在用于搅动湍流流态中的大气泡的 Ishii Zuber 模型中。