求解数据插值
许多操作都需要将求解数据插值到不同组的网格点之间。例如,重构操作需要将现有求解数据插值到新的网格上。数据插值还发生在区域之间的交界面处,其中,接触边界会交换数据。此外,可配置数据映射器可用于将场函数和表格数据插值到指定的网格。
Simcenter STAR-CCM+ 将求解数据从一组网格点(源模板)插值到另一组网格点(目标模板)。定义源模板或目标模板的一组点可以包括网格节点、网格单元形心,或面形心。例如,对于具有面模板的一组源表面,源模板包含属于源表面的所有面的形心。对于具有节点模板的一组源表面,源模板包含位于源表面上的所有网格节点。
在某些情况下(例如重构和手动数据映射),Simcenter STAR-CCM+ 可选择用于传输数据的插值方案。可用的插值方案会因源模板和目标模板(面、网格单元或节点)而有所不同,如下表中所列:
| 源模板 | ||||
| 节点 | 面 | 网格单元 | ||
| 目标模板 | 节点 |
|
|
|
| 面 |
|
|
||
| 网格单元 |
|
|
|
|
以下章节介绍了节点到面映射的上下文中的形状函数格式。面到面映射的上下文中介绍了所有其他格式。该公式可以广义化至其他模板组合。
在所有图中,蓝色网格(源网格)上的求解场被插值到红色网格(目标网格)。
最近邻插值
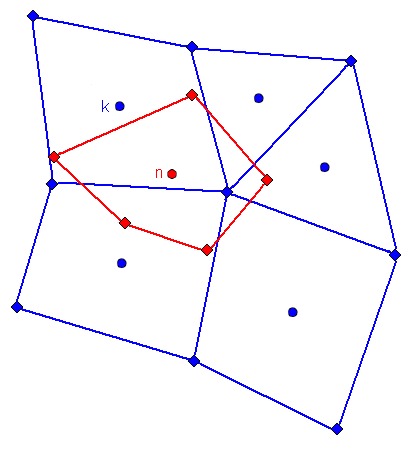
最小二乘插值
为了计算目标点 处的映射值,Simcenter STAR-CCM+ 使用一阶泰勒级数对求解场 求近似值,该一阶泰勒级数以 为中心:
只有与最靠近目标面的源面相邻的面才能参与插值。在 Eqn. (5227) 中, 标明参与面的形心组。
在图表中,面 0 最靠近面 a。仅当面 0 的相邻面定义为与面 0 共享至少一个节点的任何面时,这些相邻面才会对插值有贡献。这些相邻面为 2、3、4、5、6 和 8。缺点是,有些压印到目标面(例如 1、10、11、7)上的蓝面不起作用。
| 注 | 最小二乘法适用于面和节点源模板的所有网格单元类型。 |
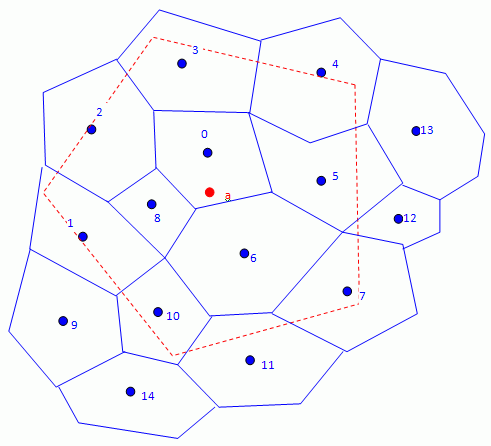
精确压印插值
为了计算目标点 处的映射值,Simcenter STAR-CCM+ 使用标准化的交面区域 作为插值权重:
表示源网格上与目标面相交的面的形心集 。为面形心 处的求解。
- 需要保持通量映射
- 源网格比目标网格更精细,且表面曲率得到充分求解
与最小二乘格式不同,压印在目标面上的所有源面均参与插值。
如果在源或目标网格中不足以求解表面曲率,使用精确压印方法进行映射可能会失败。
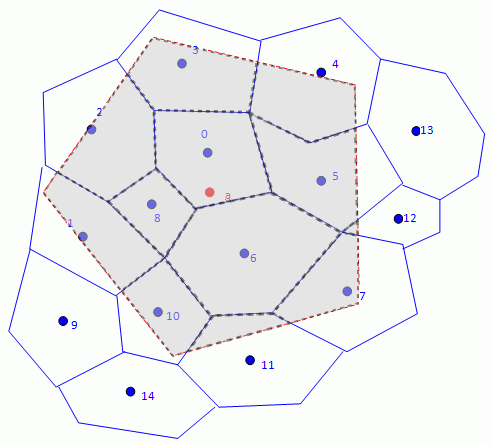
粗略压印插值
此方法为精确压印方法的变体,其中,源模板是使用接近检查(而非精确相交)构建的。接近检查需要的计算量少于精确方法。
精确压印将从模板中消除面 9、13 和 14,因为它们不与目标面相交。与精确压印一样,标准化面网格面积用作插值权重。
尽管粗略压印方法比精确压印方法更稳定,但它不能保持通量。如果源网格比目标网格更精细,则近似法的精度可与精确法媲美。
形状函数插值

为了计算目标点 处的映射值,Simcenter STAR-CCM+ 使用节点形状函数在单元 k 的节点处的求解进行插值:
其中, 为节点 处的形状函数, 为节点 处的求解值, 表示单元 k 中点 的局部坐标。总和超过了单元 k 的节点组 。
节点形状函数的形式取决于单元类型。例如,2D 的四节点等参四边形具有以下节点形状函数:
| 注 | 形状函数格式仅适用于 2D 三角形和四边形单元以及 3D 四面体和六面体。 |
使用形状函数从有限元网格进行映射时,Simcenter STAR-CCM+ 可识别单元类型并使用相关形状函数进行插值。Simcenter STAR-CCM+ 支持具有中间边节点的二次元。然而,当映射至有限元网格时,Simcenter STAR-CCM+ 仅使用拐角节点值进行参数化映射,而不考虑中间边节点。
保守封闭面
插值法通常用于将数据从精细有限体积网格映射到粗糙有限元网格的情况。一般要求源面数至少是目标节点数的三倍。
此方法标记每个目标单元(红色)以及面形心位于该单元内部的所有源面(蓝色)。源面使用节点距离法的倒数对此单元的所有顶点作贡献。额外的保守约束可确保物理量的守恒。
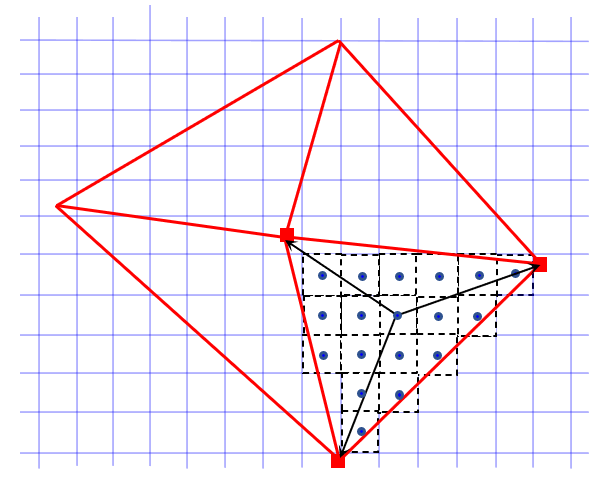
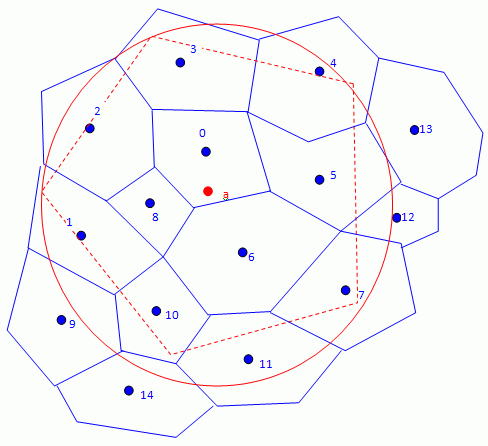
保守最大距离
插值法通常用于将数据从精细有限体积网格映射到粗糙有限元网格的情况。一般要求源面数至少是目标节点数的三倍。
此方法在由影响节点数和最大距离定义的圆内搜索每个源面(蓝色)的影响节点,如下所示:
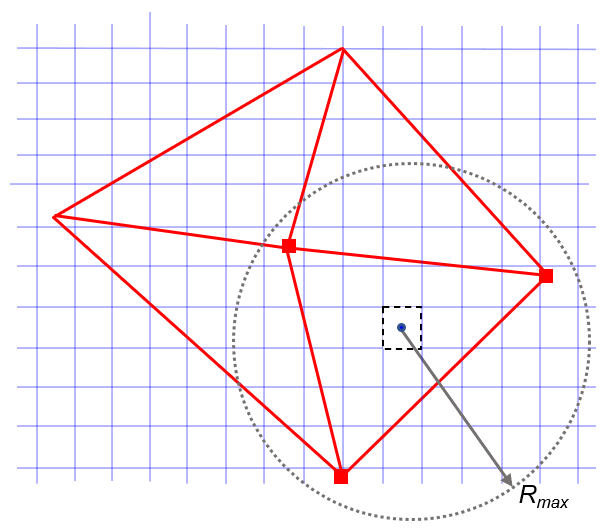
在对所有源面进行循环后,每个粗糙网格节点上的映射场将根据其影响面计算为求解的加权和。插值权重基于具有保守约束的距离的有理函数。
守恒校正
守恒校正应用于插值求解,以确保网格重构后会守恒大量物理变量(例如质量、动量、总能量)。
对于质量和质量分数,守恒方程定义为:
其中
为组分指数。
为旧网格的 网格单元中的密度。
为旧网格的 网格单元中 组分的质量分数。
为新网格的 网格单元中的密度。
为新网格的 网格单元中 组分的质量分数。
且
对于动能,守恒方程定义为:
其中
为速度分量。此公式对于所有速度分量 有效。
对于总能量,守恒方程定义为:
对于绝对压力,体积守恒方程定义为:
总焓 因守恒方程而守恒
Eqn. (5238) 和Eqn. (5239)。