标量、矢量和张量
Simcenter STAR-CCM+ 中的大多数物理量都是标量、矢量或二阶张量。
- 标量
- 标量是完全由其幅值定义的物理量。
- 矢量
- 矢量是完全由其幅值和方向定义的物理量。 例如,电场和速度为矢量。
- 张量
- 张量是完全由其在不同作用面上的幅值和方向定义的物理量。 例如,应力和应变为张量。 与标量和矢量一样,张量可能取决于其他变量,如空间和时间。 在这种情况下,可以使用张量函数描述张量。
矢量和张量表示
由于矢量和张量是方向物理量,因此相对于坐标系定义这些物理量十分方便(请参见坐标系)。
在 3D 欧几里德空间中,矢量 可以写为:
(5184)
其中, 为坐标系中的基矢量(例如,笛卡尔坐标系的单位矢量 ), 为 相对于基矢量的分量。
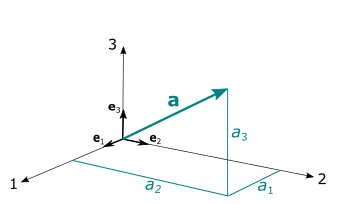

此公式使用爱因斯坦求和约定,这意味着对一组重复指数求和:
(5185)
同样,二阶张量 可以写为:
(5186)
其中, 为基矢量之间的双积或张量积(请参见 Eqn. (5196))。
Eqn. (5184) 和 Eqn. (5186) 采用指数记数法,也称为张量记数法。 标识张量分量所需的指数数量定义了张量的阶数。 实际上,可以将标量和矢量分别视为 0 阶和 1 阶张量。
对于张量分量 ,第一个指数标识分量的作用面,而第二个指数标识方向。 例如,以笛卡尔坐标系 中的应力张量分量 为例:
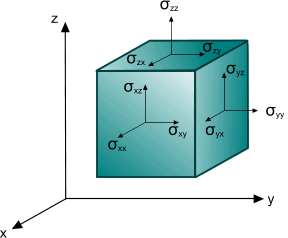

分量 标识 方向上作用于垂直于 轴的平面(即,平面 )的应力分量。 分量 标识 方向上作用于垂直于 轴的平面(即,平面 )的应力分量。
方便记数法指相对于矢量基将矢量和张量的分量表示为矩阵。 在矩阵表示中,会隐含基矢量。
在 3D 欧几里德空间中,矢量 的分量可以表示为长度为 3 的一维组分表:
(5187)
称为 的列矢量表示。 还可以使用行矢量表示来定义矢量 :
(5188)
选择使用行还是列表示纯粹由习惯决定。 可通过定义行和列表示,将两个矢量之间的标量积和双积写为矩阵积(请参见常见运算)。
在 3D 欧几里德空间中,二阶张量 的分量可以表示为 3x3 矩阵:
(5189)
张量可以定义为协变或逆变,具体取决于其分量如何随坐标系的更改而转换。 此形式化描述超出了本概述的目的。