理想化

在许多模拟中，常规做法是通过使用对称平面、旋转轴、周期性或将 3D 域减小到 2D 域来减小计算域的大小。但是，在使用报告计算物理量时，通常要考虑整个域。可以使用理想化获取完整模型的报告值。

拉伸理想化

拉伸理想化可用于评估通过拉伸 2D 区域获得的 3D 域的报告。要定义拉伸，可指定拉伸厚度和螺距，即单位拉伸厚度的旋转角度。

螺距 ( θ ) 对计算标量的报告没有影响。对于计算矢量的报告，该物理量由矢量定义：
图 1. EQUATION_DISPLAY
F = ( F ′ x c − F ′ y s ) i + ( F ′ x s + F ′ y c ) j + F ′ z h k  
(5240)

其中 F ′ x 、 F ′ y 和 F ′ z 分别为 x、y 和 z 中的理想化矢量分量； F 是去理想化矢量； h 为总拉伸厚度， c 和 s 定义如下：

c = h sin ⁡ Δ θ Δ θ
s = h 1 − cos ⁡ Δ θ Δ θ

Δ θ 为拉伸厚度上的总螺距。

如果指定负拉伸厚度，则 2D 区域在理想化坐标系 − Z 方向上的拉伸距离为 | h | 。Simcenter STAR-CCM+ 采用符号值 h 来计算 θ 中的变化；这可确保正螺距始终表示沿 Z 正方向的逆时针扭转。

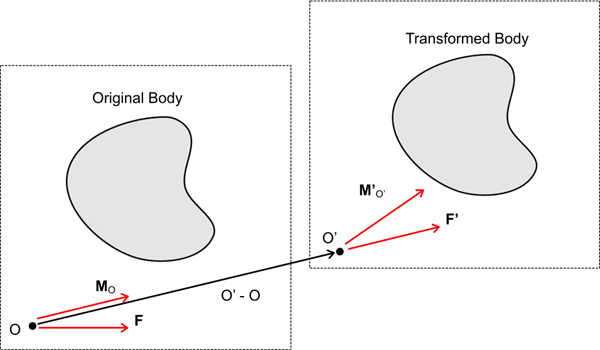
将理想化应用于具有螺旋拉伸的力矩或磁扭矩报告时，理想化的力将平移到螺旋拉伸的旋转轴。平移的力可产生新力矩。力和新力矩根据 Eqn. (5240) 转换。转换的力将重新平移到原始力矩原点，这会在新的力矩计算中产生附加项。有关更多信息，请参见力矩转换。

周期理想化

只要在边界交界面中检测到周期交界面，就会创建周期理想化。周期理想化可用于评估整个几何的报告，前提是仅对几何较短的重复段进行建模。有关更多信息，请参见周期交界面拓扑。

将周期理想化应用于标量报告时，标量将乘以周期重复次数（即捕捉完整模型的重复段数） N 。周期重复次数等于 360 度除以周期重复角度（重复段的内角）。如果周期重复角不是因子 360，则结果定义不明确。

如果将周期理想化应用于矢量，则会生成矢量的 N 个副本，其中每个副本都相对于上一个副本以周期重复角度旋转。添加生成的矢量以获取理想化报告矢量。例如，当周期重复角度为 60 度时，生成原始矢量报告的 6 个副本（以 0、60、120、180、240 和 300 度旋转）。

对于计算力矩的报告，其公式与矢量计算相同，但也同时考虑力矩矢量旋转时力矩原点的转换。

对称理想化

只要 Simcenter STAR-CCM+ 检测到对称边界，就会创建对称理想化。对称理想化可用于评估整个几何的报告，前提是仅对一个由对称线包围的小部件进行实际建模。

当应用于随输入部件范围（如体积积分物理量）缩放的标量时，理想化将物理量乘以 2 n （其中 n 为对称平面数）。

对于矢量（如力），Simcenter STAR-CCM+ 将连续反映每个对称平面上的矢量，并将反映的矢量添加到计算的原始矢量。

将理想化应用于力矩时，对于每个对称平面，Simcenter STAR-CCM+ 都会执行以下操作：
  • 通过忽略平面外分量来反映力矢量。
  • 通过忽略其平面内分量来反映力矩。
  • 通过忽略相对于对称平面的平面外坐标来反映力矩原点。
  • 计算对于原始力矩原点反映的力的力矩以获取平移项。
  • 将反映的力矩和平移项添加到原始力矩计算中。
  • 将反映的力添加到原始力中。
  • 将获得的力和力矩用作力和力矩输入，以计算下一个对称平面的理想化。
反映了力、力矩和原点后，Simcenter STAR-CCM+ 将按照力矩转换中的描述计算转换的力矩。

力矩转换

因力系转换而产生的对于 O 点的力矩 ( M ′ ) 可以由对于 O 的原始力矩 M O 计算得出（即由原始力而产生的力矩）。将转换直接应用于 M O 可对转换的力矩原点产生转换的力的力矩 M ′ O ′ 。然后，可以按如下方法计算力矩 M ′ O ：
图 2. EQUATION_DISPLAY
M ′ O = M ′ O ′ + ( O ′ − O )   × F ′
(5241)
其中 F ′ 为转换的力系。