虚拟质量

周围流体的惯性会影响浸入在流体中的颗粒的加速度。在无粘性流理论中，此效应可表示为“虚拟质量”或“附加质量”，等于常数乘以颗粒移动的流体质量。

将此“虚拟质量力”包括在内可使加速流动的流体更接近实际 [496]。例如，该虚拟质量项会影响稳态旋流中气泡的轨线。由于虚拟质量项缩小了跨不同相的响应时间尺度的范围，因此它还可以通过降低非加速流体对动量或压力松弛因子的灵敏度，帮助其收敛。

虚拟质量力的两相公式基于 Auton 等人的 [430]。此公式还可应用于存在一个连续相和多个稀释离散相的多相环境中。对于非稀释系统，它仍可以给出有用的一级近似，尤其是当虚拟质量系数包含针对颗粒浓度的校正时。

相对于相 $j$ 的加速度导致的作用于相 $i$ 的虚拟质量力如下：

图 1. EQUATION_DISPLAY

{F_{i j}}^{V M} = C_{VM} ρ_{c} α_{d} (a_{j} - a_{i})

(1996)

其中：

$c$ 为相间相互作用 $i j$ 中的连续相。

$d$ 为相间相互作用 $i j$ 中的离散相。

$C_{VM}$ 为相互作用 $i j$ 的虚拟质量系数。

$a_{i} 和 a_{j}$ 分别为相 $i$ 和 $j$ 的加速度。

虚拟质量的加速度项基于恒定质量颗粒的速度变化率，在固定坐标系中，该项将变为材料导数：

图 2. EQUATION_DISPLAY

a_{i} = {(\frac{D v}{D t})}_{i}

(1997)

但是，对于相间质量传递可导致颗粒质量增加或减少的应用，必须广义化 $a_{i}$ 。要实现这一目的，首先需要使得恒定控制体积内包含的相动量平衡。跨相到相交界面的动量通量可以标识为与跨相与控制体积外表面之间的交界面的动量通量类似的项。这会导致相 $i$ 对所有其他应用力的反应的总惯性项定义如下：

图 3. EQUATION_DISPLAY

ρ_{i} α_{i} a_{i} = \frac{\partial}{\partial t} ρ_{i} α_{i} v_{i} + \nabla \cdot (ρ_{i} α_{i} v_{i} v_{i}) - \sum_{i}^{} m_{ij} v_{ji}

(1998)

其中：

$m_{ij}$ 为从相 $i$ 到相 $j$ 的单位体积相间质量传递率。

$v_{ij}$ 为相间速度值。

从离开一个相的动量通量与进入另一个相的动量通量达到平衡这个意义上讲，以下闭合方程满足动量守恒：

图 4. EQUATION_DISPLAY

v_{ij} = {\begin{matrix} \begin{matrix} v_{j} m_{ij} > 0 \end{matrix} \\ \begin{matrix} v_{i} m_{ij} < 0 \end{matrix} \end{matrix}

(1999)

包含相间质量传递导致的动量通量的全加速度项随即变为：

图 5. EQUATION_DISPLAY

a_{i} = {(\frac{D v}{D t})}_{i} + \frac{1}{ρ_{i} α_{i}} \sum_{l}^{} m_{ij} ({v_{i} - v}_{ij})

(2000)

球形颗粒虚拟质量系数

根据无粘性流理论 [496]，在无界限三维流体中加速的球形颗粒的虚拟质量系数如下：

图 6. EQUATION_DISPLAY

C_{VM, sphere} = 0.5

(2001)

此函数限于用于跨广泛体积分数的稳定求解，方法为指定最小自由流分数 $γ_{m i n}$ （默认值为零）。

图 7. EQUATION_DISPLAY

C_{VM} = {[{(C_{VM, sphere})}^{- 2} + C_{VM, \max} {(α_{c}, γ_{m i n})}^{- 2}]}^{- 1 / 2}

(2002)

Zuber 虚拟质量系数

Lamb 的 [496] 为跨外部固定球体的中心的内部球体加速提供了无粘性流求解。 Zuber 的 [578] 使用此求解计算了无穷多个颗粒的虚拟质量系数。球体直径比的立方表示体积分数。

使用单个离散相的体积分数的结果如下：

图 8. EQUATION_DISPLAY

C_{VM, Zuber} = 0.5 \frac{1 + 2 α_{d}}{1 - α_{d}}

(2003)

此函数改写后可用于多相计算，改写方法为将 $α_{d}$ 替换为离散相体积分数的总和：

图 9. EQUATION_DISPLAY

\sum α_{d} = 1 - α_{c}

(2004)

然后，当 $α_{c} \to 0$ 时，应用稳定性限制器：

图 10. EQUATION_DISPLAY

C_{VM, Zuber} = 0.5 \frac{3 - {2 α}_{c}}{α_{c}}

(2005)

图 11. EQUATION_DISPLAY

C_{VM} = {[C_{VM}^{- 2} + C_{VM, \max} {(α_{c}, γ_{m i n})}^{- 2}]}^{- (1 / 2)}

(2006)

理论上“自由流”分数的默认值为 $γ_{m i n} = - 10$ 。这使得 Zuber 虚拟质量系数在应用限制前，可表示有效范围 $0 < \sum α_{d} < 0.66$ 中，总颗粒浓度对虚拟质量力的影响。

在模拟中，选定的虚拟质量系数可以绘制为场。

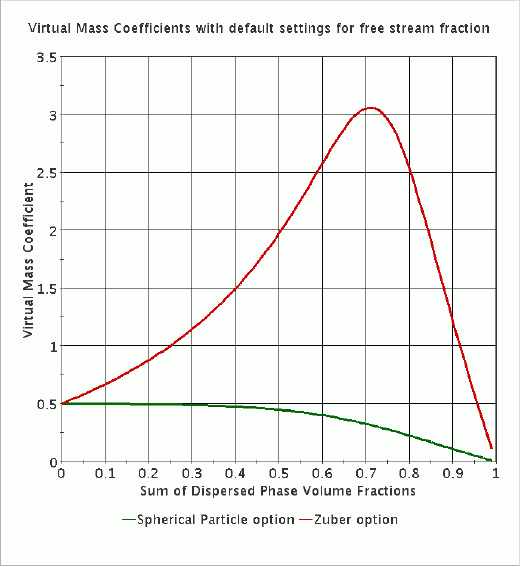
默认选项为球形颗粒法，该法基于球形颗粒的标准系数 0.5。出于稳定性考虑，在高离散相浓度情况下将减小该系数。

在对加速流体中不断增加的颗粒浓度或多个离散相的效应进行建模时，Zuber 选项可提高建模精度。

下图对这两个模型得到的虚拟质量系数进行了比较，每个模型都使用其自己的自由流分数 $γ_{m i n}$ 的默认值作为稳定性限制。

旋转坐标系中的虚拟质量项

用于多参考坐标系 (MRF) 应用时，上面定义的虚拟质量力项修改如下。此修改基于绝对速度公式，该公式使用在旋转坐标系 $R$ 中推导的动量方程，直接求解惯性坐标系 $I$ 中的速度。

图 12. EQUATION_DISPLAY

{F_{i j}}^{V M} = C_{VM} ρ_{c} α_{d} [{a_{j}}^{I R} - {a_{i}}^{I R}] + C_{VM} ρ_{c} α_{d} ω \times [{v_{j}}^{I} - {v_{i}}^{I}]

(2007)

其中， $ω$ 为旋转坐标系的角速度，旋转坐标系中的相 k 加速度采用绝对速度定义如下：

图 13. EQUATION_DISPLAY

{a_{k}}^{I R} = {[\frac{D}{D t} {v_{k}}^{I}]}_{k}^{R} + \frac{1}{ρ_{k} α_{k}} \sum_{l}^{} m_{k l} ({v_{k}}^{I} - {v_{k l}}^{I})

(2008)

图 14. EQUATION_DISPLAY

{[\frac{D}{D t} ϕ]}_{k}^{R} = \frac{\partial ϕ}{\partial t} + {v_{k}}^{R} \cdot \nabla ϕ

(2009)

虚拟质量应力

上述各项描述了平均流加速度（如发展流中发生的或旋流导致的）的虚拟质量效应。但是，在颗粒对湍流波动做出的局部瞬时响应中，同样存在虚拟质量效应。可通过进一步的虚拟质量应力项来描述其对雷诺平均相动量方程的影响。

（离散相中）瞬时虚拟质量力如下：

图 15. EQUATION_DISPLAY

F_{v m s} = ρ_{c} C_{VM} α_{d} (\frac{\partial v_{c}}{\partial t} + v_{c} \cdot \nabla v_{c} - \frac{\partial v_{d}}{\partial t} - v_{d} \cdot \nabla v_{d})

(2010)

其中，下标 $c$ 和 $d$ 分别表示连续相和离散相。

Eqn. (2010) 的雷诺平均将生成多个项。尽管虚拟质量力考虑了平均流的加速度，但波动协方差由以下表达式给出：

图 16. EQUATION_DISPLAY

〈 α_{d} v_{d}^{"} \cdot \nabla v_{d}^{"} 〉, 〈 α_{c} v_{c}^{"} \cdot \nabla v_{c}^{"} 〉

(2011)

在进行一些代数运算后得到：

图 17. EQUATION_DISPLAY

〈 F_{v m s} 〉 = ρ_{c} C_{VM} {\bar{α}}_{d} (\frac{1}{{\bar{α}}_{c}} \nabla\cdot {\bar{α}}_{c} σ_{c} - \frac{1}{{\bar{α}}_{d}} \nabla\cdot {\bar{α}}_{d} σ_{d})

(2012)

其中， $σ_{c}$ 和 $σ_{d}$ 为对应相的雷诺应力， $〈 F_{v m s} 〉$ 为虚拟质量应力项。

虚拟质量系数限制

为了将虚拟质量力作为目标相间力处理，Cook 和 Harlow 的 [442] 构造了一个替代虚拟质量项，构造方法为将三场（离散相、连带连续相和总体连续相）模型收缩成两场模型。

当与离散相关联的虚拟质量超过了连续相的总质量时，Cook 和 Harlow 公式将变为奇异公式。这不一定是物理约束，且它不适用于其他虚拟质量公式，例如基于 Auton 等人的 [430] 的公式。然而，考虑虚拟质量力是多相动量方程的重要校正的最大颗粒浓度时，可以使用连带流体分数和自由流流体分数的 Cook 和 Harlow 概念作为起点。假设存在一个连续相，并且用于虚拟质量系数 $C_{VM}$ 的同一模型将用于所有离散相。 “自由流”流体（即，在离散相上未连带成为“附加质量”的部分）的分数如下：

图 18. EQUATION_DISPLAY

γ = \frac{α_{c} - C^{V M} \sum α_{d}}{α_{c}}

(2013)

然后，根据自由流体的分数 $γ$ 不小于某最小值 $γ_{m i n}$ 这一合理假设获取虚拟质量系数的上限：

图 19. EQUATION_DISPLAY

C_{VM, \max} (α_{c}, γ_{m i n}) = \frac{α_{c}}{1 - α_{c}} (1 - γ_{m i n})

(2014)

选择 $γ_{m i n} = 0$ 时，将给出连续相体积分数的有效使用范围 $1 \leq α_{c} \leq 0.5$ ，在该范围内，可以在约束开始限制系数之前应用典型虚拟质量系数 $C_{VM} = 0.5$ 。超出此范围，随着连续相体积分数逐渐为零，该约束将使虚拟质量力逐渐为零，从而有助于保持稳定性。

虚拟质量系数基于流体场中的动能含量，因此仅从连带质量的角度考虑该系数不会始终有用。超过 Cook 和 Harlow 限制 $γ_{m i n} = 0$ 的强虚拟质量效应在紧密填充的颗粒 [578] 或塞状流 [479] 中可确实存在。此类高虚拟质量系数的物理解释为，颗粒的相对加速度差可以导致流体通过颗粒之间或颗粒与壁面之间的有限间隙回流，或者局部峰值速度高于相间的平均相对滑移速度数倍。在这些条件下，通过使用负值 $γ_{m i n}$ 松弛约束可查看在求解不会变得不稳定的条件下，精度可提高的程度。