相间相互作用拓扑

双流体模型提供了一个灵活的框架，其中离散、分层或混合的两相流可以通过使用适当的封闭关系来建模。对于给定的一对相，Simcenter STAR-CCM+ 中的欧拉多相流 (EMP) 模型可以对不同类型的相拓扑进行建模。

连续离散

连续-离散拓扑提供了在整个域中在任何时候，对离散在另一相中的一个相的相互作用进行建模的方式。

在以下方程中，下标 $c$ 表示连续相，下标 $d$ 表示离散相。下标 $i j$ 描述相 $i$ 和相 $j$ 之间的相互作用，其中 $i$ 和 $j$ 可以是连续相或离散相。

多流态

多流态拓扑是一种扩展拓扑定义，其中可以对所有类型的多相流（即离散流，例如气泡、液滴和颗粒流，和混合/分层流，例如自由表面流）进行建模。上一节的图中显示了这种多流态拓扑的一个例子。

为了实现这种组合模拟，流拓扑必须分为离散和中间的两相流两类。Simcenter STAR-CCM+ 采用基于体积分数的标准将流态分为离散和中间两相流两类。

作为第一步，离散和中间两相流的共存要求一对相必须是一组主相 ( $p$ ) 和次相 ( $s$ )，而不是一对连续相和离散相。根据此定义，对于一对主相和次相，可以定义三个流态：


流态	流拓扑
第一离散流态	次相分散在主相中。
中间流态	两个相互不分散到彼此内部的区域。
第二离散流态	主相分散在次相中。

在多流态拓扑的中间流态中，两个相明确互不分散到彼此内部的区域。中间流态默认对混合流进行建模。要对分离的流建模，需要使用大尺度交界面 (LSI) 的附加建模。流态分类标准是使用混合加权函数的定义隐式定义的，下一节将对此进行讨论。

混合加权函数

要更清楚地了解此流态定义，将水系统视作主相，将空气视作次相。在这种情况下，多流态模型处理第一离散状态下的气泡流、第二离散状态下的液滴流，以及大尺度交界面状态下分离的水气流。

为了在每个计算网格单元中强制进行流态分类，通过使用每个流态拓扑结构的相互作用的加权总和来计算总的线性化曳力系数 $A$ 和热传递系数 $h$ ，如下所示：

图 1. EQUATION_DISPLAY

A = \sum_{r = fr, ir, sr} W_{r} A_{r}

(1914)

图 2. EQUATION_DISPLAY

h = \sum_{r = fr, ir, sr} W_{r} h_{r}

(1915)

其中， $W_{r}$ 为权重函数。

下列加权函数方法可用：

标准混合函数
基于梯度的混合函数
用户指定的混合函数

标准混合函数

在中间流态中对混合流建模时，此混合函数适用。

继 Höhne 和其他人 [476] 的工作之后，每个流拓扑结构的权重函数按如下所述计算。

第一离散流态混合加权函数 $W_{f r}$ ：

图 3. EQUATION_DISPLAY

W_{f r} = \frac{1}{1 + e^{B (α_{s} - α_{f r t})}}

(1916)

其中：

$α_{s}$ 为次相的体积分数。
$α_{f r t}$ 为第一离散流态结束，即 $α_{s}$ 的值，在此处，第一离散流态过渡到中间流态。根据文献 [439]，默认值为 0.3。

第二离散流态混合加权函数 $W_{s r}$ ：

图 4. EQUATION_DISPLAY

W_{s r} = \frac{1}{1 + e^{B (α_{s r o} - α_{s})}}

(1917)

其中：

$α_{s r o}$ 为第二离散流态的开始。它对应于 $α_{s}$ 的值，在此处，交界面流态过渡到第二离散流态。根据文献 [439]，默认值为 0.7。

中间区混合加权函数 $W_{i r}$ 计算如下：

图 5. EQUATION_DISPLAY

W_{i r} = 1 - (W_{f r} + W_{s r})

(1918)

两个阈值 $α_{f r o}$ 和 $α_{s r t}$ 可灵活地控制各个流态的范围。可以通过更改指数 $B$ 控制过渡区域的宽度：增加 $B$ 会减小过渡区域的宽度。使用 $B = 70$ 默认值时，过渡边界的宽度为 $α = 0.2$ 。

取决于次相体积分数的权重函数如以下绘图所示：

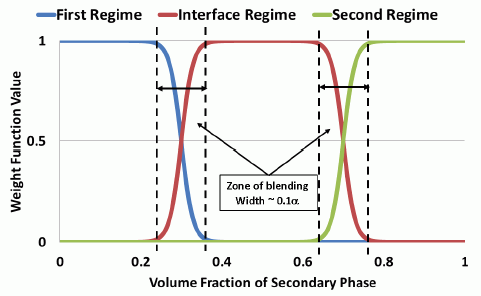
基于梯度的混合函数

在中间流态中对分离流建模时，此混合函数适用。

继 P. Porombka 和 T. Höhne [476] 的工作后，标准加权函数通过合并基于梯度的校正进行了扩展。基于梯度的修改实质上会带来更平滑的混合加权函数场。

每个流拓扑结构的加权函数计算如下：

图 6. EQUATION_DISPLAY

W_{f r} = \frac{1}{1 + e^{B (α_{s} - α_{f r t})}} \cdot \frac{1}{(1 + c_{g} | \nabla α_{s} |)}

(1919)

图 7. EQUATION_DISPLAY

W_{s r} = \frac{1}{1 + e^{B (α_{s r o} - α_{s})}} \cdot \frac{1}{(1 + c_{g} | \nabla α_{s} |)}

(1920)

图 8. EQUATION_DISPLAY

W_{i r} = 1 - (W_{f r} + W_{s r})

(1921)

Eqn. (1919) 和 Eqn. (1920) 中的因子 $c_{g}$ 控制了混合函数中梯度的角色。默认值为 $c_{g} = 0.05$ 。此基于梯度的混合函数不能在 XY 绘图上客观地进行绘制，因为它涉及体积分数梯度计算。

用户指定的混合函数

用户使用场函数指定 $W_{f r}$ 和 $W_{s r}$ 。中间区加权函数 $W_{i r}$ 在内部计算，如下所示：

$W_{i r} = 1 - (W_{f r} + W_{s r})$

Simcenter STAR-CCM+ 会执行内部检查，确保 $0 \leq W_{f r} \leq 1$ 、 $0 \leq W_{s r} \leq 1$ 和 $0 \leq (W_{f r} + W_{s r}) \leq 1$ 。