初始和边界颗粒尺寸分布

Simcenter STAR-CCM+ 对初始条件进行一次采样，然后尝试使用一些组来近似每种方法的累积分布。它在每次迭代时对流入条件重新采样，可以根据边界旁边的收敛流内的条件贡献给不同大小的组。

AMUSIG 方法是基于体积的方法，即：在每个点上，所有尺寸组均具有大致相同的体积分数。初始条件和边界条件也据体积分布进行设定。直径小于或等于 $d$ 的所有颗粒（液滴、气泡）的体积分数为：

其中，${\alpha }_d$ 为离散相的体积分数，$F\left(d\right)$ 为累积尺寸分布 (CSD)。

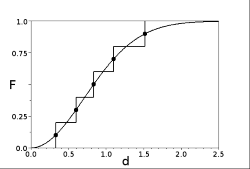
AMUSIG 方法表示离散相作为尺寸组的整体，因此该方法的 CSD 具有阶梯形状，如下所示。

表 1. 通过 AMUSIG 方法得出的 Rosin-Rammler 分布及其近似：5 个尺寸组（左）和 20 个尺寸组（右）。

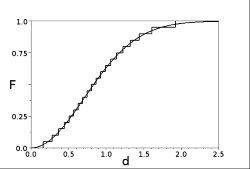$F$ 增量的位置对应于相应尺寸组的组直径；$F$ 的所有增量均具有相同的高度。

为了通过 AMUSIG 方法近似连续分布，假设每个增量的中间（5 个尺寸组图（左上）中的点）属于该曲线。对于 $M$ 尺寸组，$i^{th}$ 尺寸组的直径将计算为以下方程的求解：

近似的质量随着尺寸组数而增加。但是，可以确认较少组数（例如 $M=5$）捕捉的分布的主要特征，例如 $d_{43}$、$d_{32}$。

下面介绍了 AMUSIG 方法中使用的分布。

均匀分布

此分布假设颗粒在最小尺寸和最大尺寸之间均匀分布：

$$F\left(d\right)=\{\begin{array}{ccc}0& ,& d<d_{\min }\\ \frac{(d-d_{\min })}{(d_{\max }-d_{\min })}& ,& d_{\min }\le d\le d_{\max }\\ 1& ,& d>d_{\max }\end{array}$$

(2296)

其中，$d_{\min }$ 为最小直径，$d_{\max }$ 为最大直径。

大多数情况下建议均匀分布，因为这样可以轻松控制尺寸分布。在许多情况下，初始（入口）分布只是近似已知，对求解影响不大，因此指定最大尺寸和最小尺寸便已足够。

均匀分布的平均直径为：

$$d_{pq}=\sqrt[p-q]{\frac{(q-2)(d_{\max }^{p-2}-d_{\min }^{p-2})}{(p-2)(d_{\max }^{q-2}-d_{\min }^{q-2})}}$$

(2297)

特殊设置：

$$\begin{array}{cc}{d}_{43}=\frac{d_{\max }+d_{\min }}{2},& d_{32}=\frac{d_{\max }+d_{\min }}{\ln \left(d_{\max }\right)-\ln \left(d_{\min }\right)}\end{array}$$

(2298)

Rosin-Rammler 分布

Rosin-Rammler 分布，也称为威布尔分布，为：

$$F\left(d\right)=1-\exp (-{\left[\frac{d}{D_{\text{ref}}}\right]}^k)$$

(2299)

其中， $k$ 为形状参数， $D_{\text{ref}}$ 为尺寸参数。

此分布广泛用于粉碎过程的颗粒尺寸分析。在 $k=1$ 的特定情况下，它将变为指数分布。参数 $D_{\text{ref}}$ 具有长度维度，指定特征尺寸，而参数 $k$ 为无量纲，控制分布的扩散（较高的 $k$ 意味着较窄的分布）。

Rosin-Rammler 分布的平均直径为：

$$d_{pq}=D_{\text{ref}}\sqrt[p-q]{\frac{\mathrm{\Gamma }\left(\frac{p-1}{k}\right)}{\mathrm{\Gamma }\left(\frac{q-1}{k}\right)}}$$

(2300)

其中， $\mathrm{\Gamma }$ 为欧拉 Gamma 函数。可以看到，$d_{pq}$ 仅针对 $\begin{array}{cc}p>1,& q>1\end{array}$ 确定。特殊情况：不会针对 Rosin-Rammler 分布确定 $d_{10}$ 和 $d_{30}$。

对数正态分布

对数正态分布意味着直径的对数具有平均值 $\mu$ 和标准偏差 $\sigma$ 的正态分布。CSD 的公式为：

$$F\left(d\right)=\frac{1}{2}+\frac{1}{2}\mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{\ln d-\mu }{\sqrt{2}\sigma }\right)$$

(2301)

对数正态分布的平均直径为：

$$d_{pq}=\exp (\mu +\frac{1}{2}(p+q-6){\sigma }^2)$$

(2302)

上述方程提供了一种将对数正态分布拟合到实验数据中的简单方法。已知两个不同的直径，例如 $d_{pq}$ 和 $d_{st}$，可获得以下方程：

$$\begin{array}{cc}\frac{d_{pq}}{d_{st}}=\exp \left(\frac{1}{2}(p+q-s-t){\sigma }^2\right),& {\sigma }^2=2\frac{\ln \left(\frac{d_{pq}}{d_{st}}\right)}{p+q-s-t}\end{array}$$

(2303)

将 ${\sigma }^2$ 代入先前的方程可得出（进行一些代数运算后）：

$$\mu =\frac{6-s-t}{p+q-s-t}\ln \left(d_{pq}\right)+\frac{p+q-6}{p+q-s-t}\ln \left(d_{st}\right)$$

(2304)

用户指定的直径分布

可将累积尺寸分布 (CSD) 指定为表。表的第一列包含直径 [ $d_0$ ; $d_1$ ;…; $d_i$ ;…; $d_n$ ]。第二列包含 CSD 值 [ $F_0$ ; $F_1$ ;…; $F_i$ ;…; $F_n$ ]。这两列必须单调递增。

从累积尺寸分布的定义可以看出 $F_0=0$ 且 $F_n=1$ 。生成的 CSD 为逐段线性：

$$F\left(d\right)=\{\begin{array}{cc}0& d<d_0\\ \frac{d-d_0}{d_1-d_0}(F_1-F_0)+F_0& d_0\le d<d_1\\ \frac{d-d_1}{d_2-d_1}(F_2-F_1)+F_1& d_1\le d<d_2\\ \mathrm{...}& \mathrm{...}\\ \frac{d-d_i}{d_{i+1}-d_i}(F_{i+1}-F_i)+F_0& d_i\le d<d_{i+1}\\ \mathrm{...}& \mathrm{...}\\ 1& d>d_n\end{array}$$

(2305)