Nucleation Site Number Density
The nucleation site number density determines the number of locations on the heated surface where bubbles form, per unit area.
This is the leading factor determining the evaporation rate in a mechanistic model of subcooled boiling (see Eqn. (2110)). The diagram below illustrates this parameter:
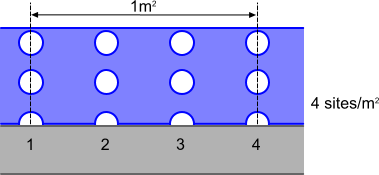
A nucleation site is a gas-filled cavity in the wall. In practice, there is a range of cavity sizes. A larger wall superheat allows bubble growth in more cavities of smaller size.
Three standard submodels have been implemented for the nucleation site number density:
- Lemmert Chawla – A correlation against wall superheat, and is often used together with the Tolubinsky Kostanchuk model for bubble departure diameter.
- Hibiki Ishii – A mechanistic model for active nucleation site number density as a function of critical cavity size and contact angle. It is designed for use with the Kocamustafaogullari model for bubble departure diameter, and is applicable up to 198 bar.
- Li – A mechanistic model based on a parametric analysis of existing experimental data. It is a function of three variables: wall superheat, pressure, and contact angle. The model is applicable for pressures ranging from 0.101 MPa–19.8 MPa.
The Lemmert Chawla model is the default option, as its fixed power for superheat dependence means that it is easier to obtain initial solutions. The more recent Hibiki Ishii model has a wider range of applicability, but it can be difficult to reach a converged solution in high flux cases. The Li model has a wider range applicability than the Hibiki Ishii model, particularly in accurately predicting results for small and moderate wall superheat values.
Under the 45 bar, 0.57 MW/m2 conditions of the first test in Bartolomei and Chanturiya [432], these two methods (each used with its recommended departure diameter model) can produce comparable results for axial void and wall superheat. However, the departure diameter that is associated with the Hibiki Ishii and Kocamustafaogullari solution is much smaller.
At higher pressures, and higher heat fluxes, the Hibiki Ishii model has an increasingly stronger dependence on wall superheat. This model often predicts a much smaller wall superheat than the Lemmert Chawla model for the same heat flux. At higher levels of wall superheat and when no limiter is applied to the nucleation site density, the Li model predicts smaller and more realistic values than the Hibiki-Ishii model.
- Lemmert Chawla
-
The original Lemmert Chawla model [528][499] for nucleation site number density is:
(2126)where:
- is the nucleation site density
- is a calibration constant, with a default value of 185.0/K
- is a superheat exponent, with a default value of 1.805
- is the wall superheat, which is calculated as:
(2127)where is the maximum superheat applied to the Lemmert Chawla model.
Simcenter STAR-CCM+ uses a modified form of the Lemmert Chawla equations. This modification allows that the superheat exponent does not have to be constant, but can itself increase significantly with wall superheat.
(2128)where:
- and are calibration constants
- is the reference nucleation site number density. The default value is 12366.44 /m2 (which is 185.01.805).
- is the reference wall superheat
You can adjust the Lemmert Chawla Method so that it is suitable for use with the Kocamustafaogullari bubble departure diameters by comparing it with the Hibiki-Ishii Method, at a given operating pressure, and for a useful range of wall superheats. For example, the table below shows a fit of the Lemmert Chawla method to the properties of water assuming a contact angle of 0.722 radians:
P (bar)
Superheat range (K) (m-2)
(K)
A B Fit Accuracy
45 1 - 10 138,100 1 1.348 0.35 7% 70 1 - 7 302,300 1 1.566 0.58 10% 150 1 - 3 5,665,000 1 3.095 1.7 0.1% Using a fitted Lemmert Chawla method instead of using the Hibiki Ishii method gives similar results. The main advantage of such a fit is that it indicates the sensitivity of either method to wall superheat as an explicit superheat exponent. For example, using the calibrations above, the table below shows that, even at 45 bar, the nucleation site number density can vary as strongly as :
P (bar) Superheat range (K) Exponent range 45 1 - 10 1.7 - 4.8 70 1 - 7 2.2 - 5.6 150 1 - 3 4.8 - 8.2 - Hibiki Ishii
-
For high wall superheats, the Hibiki Ishii method can produce extreme values of wall heat fluxes. To improve robustness, a limit is applied to the amount of superheat that can be applied:
(2129)The default value for the maximum superheat is 25K. Do not allow this limit to affect the converged solution. If necessary, adjust the limit during the calculation.
Also, use system reference pressure in place of local liquid pressure to improve robustness.
(2130)Following Hibiki and Ishii [473], the temperature of the vapor next to the wall is identified with the wall temperature.
(2131)For the contact angle between the working fluid and the surface during boiling, , Hibiki and Ishii used a value at room temperature. They suggest that a temperature dependence of contact angle is implicitly included in the calibration of the pressure effects function .
The nucleation site number density is then modeled as:
(2132)where:
- is the average cavity density, with a default value of 4.74E5 sites/m-2
- is the wall contact angle, with a default value of 0.722 radians (41.37o), which is suitable for water systems
- is the wall contact angle scale, with a standard value of 0.722 radians (41.37o)
- is the cavity length scale, with default value 2.50E-6 m
- is the logarithmic, non-dimensional density function representing the effect of pressure
- is the critical cavity radius
The critical cavity radius is:
(2133)where:
- is the surface tension
- is the vapor phase density
- is the liquid phase density
- is the liquid pressure
- is the latent heat
- is the specific gas constant for a vapor of given molecular weight.
The logarithmic, non-dimensional density function is:
(2134)where:
(2135)and:
(2136)The standard values for the density function constants are:
(2137)
- Li
The Li model ([502] for nucleation site number density is based on a parametric analysis of existing experimental data. It is a function of three variables: wall superheat, pressure, and contact angle. The model is applicable for pressures ranging from 0.101 MPa–19.8 MPa. The superheat exponent of the Li model is not constant, but can increase significantly with wall superheat.
The Li model for nucleation site number density is:
(2138)where:
- is the nucleation site density.
- is the average cavity density, with a default value of 1000 sites/m2.
- is the wall superheat.
-
is a non-dimensional function
representing the effect of pressure, given by: (2139)
- is the liquid pressure.
(2140)where:- is the wall contact angle, with a default value of 0.722 radians (41.37o), which is suitable for water systems.
- is the contact angle temperature with a default value of 647.15 K.
- is the zero contact angle temperature with a default value of 287.15 K.
and are functions based on experimental data, which can be defined as a linear correlation on pressure:
Nucleation Site Number Density Limiting
Not all nucleation sites can be active at the same time, because some of the sites can be inside areas that are covered by existing bubbles that are still attached to the wall during the growth time of the bubbles. To account for this effect, Gilman [467] proposes a correction to the nucleation site number density calculation:
where is the effective nucleation site number density after correction, is the uncorrected nucleation site number density, is the bubble departure frequency, is the bubble growth time, and is the bubble departure diameter.
However, in this model, can be very large at high pressure such that the exponential term in Eqn. (2143) becomes zero, which is unphysical. To keep the calculated nucleation site density within physical limits, a further correction is required.
The area occupied by nucleating bubbles while they are growing and attached to the wall during the growth time is:
where is the number of nucleating bubbles on the wall and is the bubble growth time.
The fraction of area and time that is occupied by nucleating bubbles in one bubble departure cycle is:
The bubble departure frequency is given by:
The maximum can be obtained from:
where is the projected area of a bubble at departure. Note that is the factor inside exponential function of Eqn. (2143). Instead of the exponential function, the following function is used to keep within :
When is much smaller than the maximum, Eqn. (2149) gives similar values to Gilman’s model. However, as approaches the maximum, Eqn. (2149) returns the maximum value, hence keeping within the physical limit.