KHRT 破碎模型

KHRT 破碎模型结合了两个子模型：一个基于开尔文-亥姆霍兹 (KH) 理论，另一个基于瑞利-泰勒 (RT) 理论。这两个破碎子模型均考虑液滴上的不稳定性增长，并为其波长和频率提供表达式。

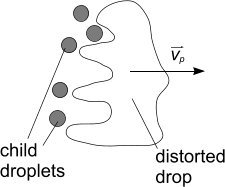
开尔文-亥姆霍兹不稳定性因液滴滑移速度而导致，这最终会从父液滴剪切出较小的子液滴 [688]，与剥离流态对应。瑞利-泰勒不稳定性因液滴加速度而导致，并易于使液滴完全破碎 [683]，与突变流态对应。KH 和 RT 子模型比较：两者导致的不稳定性可以同时增长；如果它们增长足够长时间，则会因 RT 不稳定性而发生破碎。否则，将发生 KH 破碎。

因为 KH 子模型存在生成双模尺寸分布的趋势，所以较小的子液滴将累积到新的粒子束中；父粒子束则保留较大的父液滴。但是，为了防止创建过多的子粒子束，只有当其质量达到父粒子束原始质量的预定义比例时，才会释放这些粒子束。子粒子束的横向速度需与破碎时的液滴振荡动能成比例。该速度易于从喷射器生成扩散效应。从某种程度上来说，不需要锥喷射器。

开发 KHRT 模型是为了替换 TAB 模型 [683]。尽管在低韦伯数的情况下后者仍为首选，但高韦伯数时则首选 KHRT 模型。使用该模型的主要难点是将系数调整到要考虑的应用场景。这一难点反映了物理场景的复杂性，而非模型中的缺陷所致。

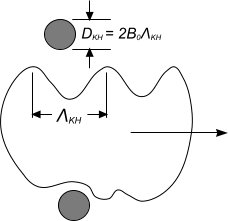
开尔文-亥姆霍兹不稳定性假定为剥离破碎的原因。

下面描述了模型示意图和关键方程。


KH 模型	RT 模型

$Child drop diameter = 2 B_{0} Λ_{K H}$	$Child drop diameter = C_{3} Λ_{R T}$
$Breakup time constant = \frac{1.894 B_{1} D_{p}}{{Λ_{K H} Ω}_{K H}}$	$Breakup time constant = \frac{C_{τ}}{Ω_{R T}}$

Reitz [688] 提出了这些不稳定性的波长和增长率的表达式：

图 1. EQUATION_DISPLAY

Λ_{K H} = \frac{4.51 D_{p} (1 + 0.45 {Oh}_{r}^{0.5}) (1 + 0.4 {Ta}_{r}^{0.7})}{{(1 + 0.865 {We}_{r}^{1.67})}^{0.6}}

(3095)

图 2. EQUATION_DISPLAY

Ω_{K H} = \frac{0.34 + 0.385 {We}_{r}^{1.5}}{(1 + {Oh}_{r}) (1 + 1.4 {Ta}_{r}^{0.6})} \sqrt{\frac{4 π σ}{3 m_{p}}}

(3096)

其中， ${We}_{r} = 0.5 We$ 为基于液滴半径的韦伯数，

图 3. EQUATION_DISPLAY

{Oh}_{r} = μ_{l} \sqrt{\frac{2}{ρ_{l} D_{p} σ}}

(3097)

为基于液滴半径的奥内佐格数， ${Ta}_{r} = {Oh}_{r} \sqrt{{We}_{r}}$ 为基于液滴半径的泰勒数。波长和增长率用于设定这些不稳定性导致的破碎的特征时间尺度和长度尺度：

图 4. EQUATION_DISPLAY

τ_{K H} = \frac{1.894 B_{1} D_{p}}{Λ_{KH} Ω_{KH}}

(3098)

图 5. EQUATION_DISPLAY

D_{K H} = 2 B_{0} Λ_{K H}

(3099)

系数 $B_{0}$ 采用值 0.61。可以调整系数 $B_{1}$ 以考虑不确定性（例如液滴初始条件中的不确定性）。文献中报告了各种不同的值，从 1.73 到 60 或更高。

如果 $D_{p} > D_{K H}$ ，可能由于 KH 不稳定性而产生破碎，在这种情况下父液滴直径根据下式减小：

图 6. EQUATION_DISPLAY

\frac{d D_{p}}{d t} = \frac{D_{K H} - D_{p}}{τ_{K H}}

(3100)

但是，仅当未发生由于 RT 不稳定性而产生的破碎（请参见下文）时，才允许发生这种情况。

KH 破碎过程中脱离的质量一直累积 [683]，直至达到父粒子束原始质量的用户指定比例（默认值为 3%）。创建一个或多个子粒子束，其子液滴直径为 $D_{K H}$ 。父粒子束液滴直径保持不变；计算液滴数以使质量守恒。还为子粒子束提供了与父粒子束原始速度垂直的速度：

图 7. EQUATION_DISPLAY

v_{⊥} = A_{1} Λ_{K H} Ω_{KH}

(3101)

可以调整法向速度系数 $A_{1}$ 以生成已知的喷射角度；也可以直接指定锥体喷射器处的喷射角度，在这种情况下 $A_{1}$ 应设为零。

瑞利-泰勒不稳定性假定为“突变”破碎的原因。按照 Senecal 等人的 [702]，Simcenter STAR-CCM+ 结合了粘度对这些不稳定性的影响。作为液滴加速度 $a$ 的函数的波数和增长率之间的关系是：

图 8. EQUATION_DISPLAY

ω_{R T} = - k_{R T}^{2} (\frac{μ_{l} + μ_{g}}{ρ_{l} + ρ_{g}}) + \sqrt{k_{R T} (\frac{ρ_{l} - ρ_{g}}{ρ_{l} + ρ_{g}}) a - \frac{k_{R T}^{3} σ}{ρ_{l} + ρ_{g}} + k_{R T}^{4} {(\frac{μ_{l} + μ_{g}}{ρ_{l} + ρ_{g}})}^{2}}

(3102)

Eqn. (3102) 进行数值求解，以给出与最大增长率 $Ω_{R T}$ 对应的波长 $Λ_{R T}$ 。这被假设为临界模式。例如，在可忽略粘度的限制下，此方法重现 [683] 使用的无粘性 RT 公式。包括粘度的理由是其效果显著；忽略粘度的实现通常需要额外的修改，例如用户自定义的破碎长度 [691]。

波长和增长率转而用于设定这些不稳定性导致的破碎的特征时间尺度和长度尺度：

图 9. EQUATION_DISPLAY

τ_{R T} = \frac{C_{τ}}{Ω_{R T}}

(3103)

图 10. EQUATION_DISPLAY

D_{R T} = C_{3} Λ_{R T}

(3104)

系数 $C_{τ}$ 采用默认值 1。系数 $C_{3}$ 采用默认值 0.1，文献中报告的值范围为 0.1-5.33。

如果 $D_{p} > D_{R T}$ ，则假设液滴上的临界瑞利-泰勒不稳定性增长。如果不稳定性持续 $τ_{R T}$ 时间，则发生破碎事件。父液滴完全破碎，生成具有新直径 $D_{R T}$ 的子液滴。