碰撞与聚结

Simcenter STAR-CCM+ 使用宿主网格单元方法检测碰撞。仅当两个粒子束位于同一网格单元中时才能发生碰撞。Simcenter STAR-CCM+ 用以下碰撞算法中速度较快的一种检测任何特定网格单元中的碰撞。以下算法可用：

• NTC（无计时器）碰撞检测算法 [699]
• 奥罗克算法 [679]

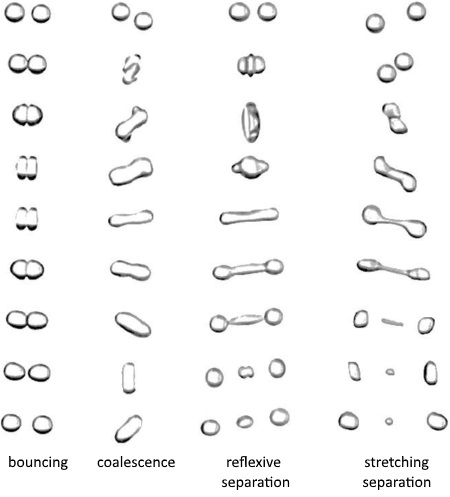
在两个液滴之间检测到碰撞后，可能会产生不同的碰撞结果：反弹、聚结、反射分离和延伸分离（擦边碰撞）[659]：

这种实施会忽略在高碰撞韦伯数下可能形成的卫星液滴。

碰撞结果由三个无量纲参数表示：

• 碰撞韦伯数 ${\text{We}}_{\text{coll}}$ 如下：

  $${\text{We}}_{\text{coll}}=\frac{{\rho }_l{\left(v_{1,2}\right)}^2(r_1+r_2)}{2\sigma }$$

  (3142)

  其中， $\sigma =\frac{1}{2}({\sigma }_1+{\sigma }_2)$ 为液滴 1 和 2 的平均表面张力， ${\rho }_l=\frac{1}{2}({\rho }_1+{\rho }_2)$ 为平均密度。相对速度 $v_{1,2}$ 如下：

  $$v_{1,2}=\left|{\mathbf{v}}_1-{\mathbf{v}}_2\right|$$

  (3143)

  其中， ${\mathbf{v}}_1$ 和 ${\mathbf{v}}_2$ 为碰撞液滴的速度， $r_1$ 和 $r_2$ 为其对应的半径。

  碰撞韦伯数还可以根据较小液滴的直径 $d_s$ 定义，相对于以下公式中给出的 ${\text{We}}_{\text{coll}}$ ：

  $${\text{We}}_d=\frac{{\rho }_l{\left(v_{1,2}\right)}^2{d}_s}{\sigma }=\frac{4\mathrm{\Delta }}{(1+\mathrm{\Delta })}{\text{We}}_{coll}$$

  (3144)
• 冲击参数 $B$ 如下：

  $$B=\frac{b}{r_1+r_2}$$

  (3145)

  其中， $b$ 计算为从一个液滴的中心到放置在另一个液滴的中心上的相对速度矢量的距离。当 $B=0$ 时，碰撞为正面碰撞。当 $B=1$ 时，液滴彼此几乎不擦边。

• 液滴尺寸比率 $\gamma$ 如下：

  $$\gamma =\frac{r_2}{r_1},r_2>r_1$$

  (3146)
  文献中常用的附加尺寸比参数是 $\mathrm{\Delta }=\frac{1}{\gamma },0<\mathrm{\Delta }<1$ 。
• 碰撞 Ohnesorge 数 $Oh$ 定义为：
  $$Oh=\frac{\mu }{\sqrt{\rho \sigma d_s}}$$
  其中 $\mu$ 为碰撞液滴的平均动力粘度。

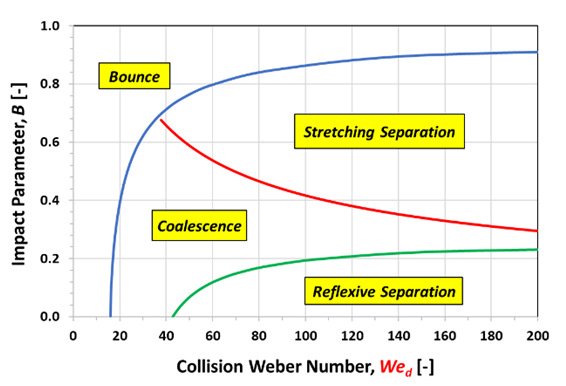
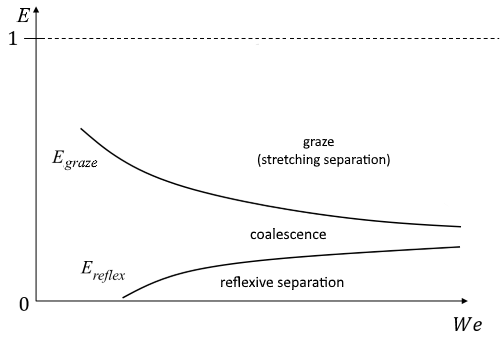
碰撞结果可以通过碰撞结果图表示，具体取决于影响参数 $B$ 和碰撞韦伯数 $\text{We}$ 。根据它们在碰撞结果图上的位置，液滴相互反弹（简单反弹或反射分离）、聚结或相互擦边（延伸分离）。曲线的常规形状可以随不同尺寸比参数以及液滴粘度等其他物理属性而变化。

Simcenter STAR-CCM+ 中实施了三个碰撞结果图。O'Rourke 图 ([678]、[671])、Ashgriz 图 ([645]) 和复合图。

O'Rourke 和 Ashgiz 图绘制碰撞效率 $E$ 与碰撞韦伯数 ${\text{We}}_{\text{coll}}$ ，通过 Eqn. (3142) 根据平均液滴直径为每对相互作用液滴计算。碰撞效率 $E$ 是由获得给定结果的概率定义的 ( $E=B\cdot B$ )。这两个图中的任何一个均不包含粘性耗散导致的能量损失效应。

O'Rourke 图

O'Rourke 图考虑了反弹、聚结和延伸/擦边分离模态。

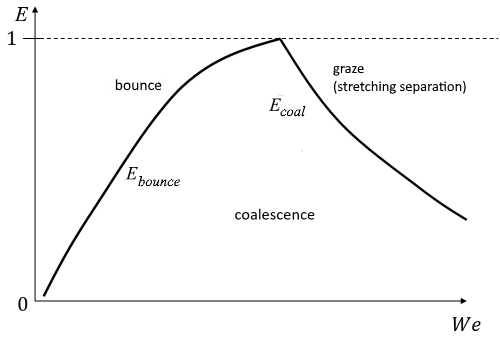
Ashgriz 图

Ashgriz 图考虑了聚结、反射分离和延伸/擦边分离模态。

聚结区域的边界由曲线 $E_{\text{coal}}$ 和 $E_{\text{bounce}}$ 或 $E_{\text{graze}}$ 和 $E_{\text{reflex}}$ 表示。

对于每条 $E$ 曲线：

其中 $A$、$a$ 和 ${\text{We}}_{\text{c}}$ 是用于将 $E$ 曲线拟合到数据的经验常数。

这些常数的默认值为：

液滴直径比率修正定义如下：

其中，$\gamma$ 为液滴大小比。常数的默认值为：

• $a_3=2.4$
• $a_2=-5.76$
• $a_1=6.48$
• $a_0=0$

使用上表中列出的 O'Rourke 的默认值，对于碰撞和聚结的这些公式的 Eqn. (3147) 的 $E_{\text{coal}}$ 和 $E_{\text{bounce}}$ 减少：

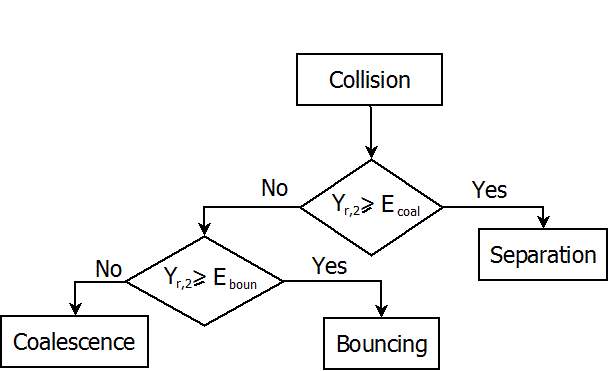
以下流程图描述了整体碰撞动力学 O'Rourke 算法 [671]：

$Y_{r,2}$ 为 [0,1] 范围内的随机数。

对于 O'Rourke 和 Ashgriz 方法，如果发生聚结，可以通过查找 $m$ 的值来确定每个液滴发生的聚结次数 $m$，且

其中，$P_n$ 为发生 $n$ 次碰撞的概率，由 Eqn. (3176) 给出。

发生聚结时，较稀疏粒子束中的液滴数量将从较密集的粒子束中减去。如果结果为擦边碰撞或反弹，则每个液滴仅计算一次碰撞。液滴的碰撞后速度、温度和质量将基于质量、动量和能量守恒进行计算。

复合图

复合图提供三条边界曲线的模型。用于反弹的 Sommerfeld 模型、用于延伸分离的 Suo-Jia 模型和用于反射分离的 Ashgriz 模型。

Sommerfeld

此模型基于 Hu 等方法 [664]，其中在临界碰撞韦伯数中考虑了能量平衡中的粘性耗散效应。

$${\text{We}}_d=\frac{g\left(\mathrm{\Delta }\right)(\mathrm{\Phi }-3)}{(1-B^2)(1-\beta )}$$

(3152)

其中：

• $g\left(\mathrm{\Delta }\right)=\frac{4(1+{\mathrm{\Delta }}^2)(1+{\mathrm{\Delta }}^3)}{{\mathrm{\Delta }}^2}$
• $\beta$ 为能量耗散因子
• $\mathrm{\Phi }$ 为与碰撞过程中液滴变形程度相关的形状因子。

Sommerfeld ([709]、[705]) 方法通过适应具有不同粘度的可用数据，自动适应 $\beta$ 和 $\mathrm{\Phi }$ ，通过 $Oh<0.5$ （对于纯液体）和 $Oh<0.4$ （对于溶液）进行限制。参数 $\beta$ 和 $\mathrm{\Phi }$ 假设为 $B$ 的线性函数。

$$\mathrm{\Phi }\left(B\right)=-k_{\mathrm{\Phi }}Oh+{\mathrm{\Phi }}_{init}Oh$$

(3153)

$$\beta \left(B\right)=(1-{\beta }_{init})Oh+{\beta }_{init}Oh$$

(3154)

$$\begin{array}{c}\begin{array}{c}{k}_{\mathrm{\Phi }}=\max (k_3{Oh}^3+k_2{Oh}^2+k_{1}Oh+k_0,k_l)\\ {\mathrm{\Phi }}_{init}=\max ({\mathrm{\Phi }}_3{Oh}^3+{\mathrm{\Phi }}_2{Oh}^2+{\mathrm{\Phi }}_{1}Oh+{\mathrm{\Phi }}_0,{\mathrm{\Phi }}_l)\\ {\beta }_{init}=\min ({\beta }_3{Oh}^3+{\beta }_2{Oh}^2+{\beta }_{1}Oh+{\beta }_0,{\beta }_l)\end{array}\end{array}$$

(3155)

这些常数的默认值为：

常数	$k_0$	$k_1$	$k_2$	$k_3$	$k_l$
纯液体	0.82	-4.03	10.93	-9.6	0.31
溶液	0.725	-10.2	52.5	-87.7	0.0834

常数	${\mathrm{\Phi }}_0$	${\mathrm{\Phi }}_1$	${\mathrm{\Phi }}_2$	${\mathrm{\Phi }}_3$	${\mathrm{\Phi }}_l$
纯液体	3.9	-4.32	12.4	-11.7	3.4
溶液	3.76	-6.05	18.31	-18.25	3.1

${\beta }_0$	${\beta }_1$	${\beta }_2$	${\beta }_3$	${\beta }_l$
0.07	5.24	-19.6	22.6	0.5

对于迎头碰撞 (B = 0)，临界韦伯数为 ${\text{We}}_d=\frac{g\left(\mathrm{\Delta }\right)(\mathrm{\Phi }-3)}{(1-\beta )}$ 。

Suo-Jia

用于延伸分离的 Suo 和 Jia ([710]) 模型仅包括无量纲参数，由以下公式给出：

$$\sqrt{{\text{We}}_d}=\frac{1}{B}(a+\frac{h}{d_s}Oh)$$

(3156)

其中 a 为 Ohnesorge 数和液滴尺寸比的函数，由以下公式给出：

$$a=(a_0-a_1\mathrm{\Delta })Oh+a_2$$

(3157)

常数的默认值为：

• $a_2=2.58$
• $a_1=180$
• $a_0=183$

此相关性适用于：

$\begin{array}{ccc}\begin{array}{c}1mPas<\mu <47.2mPas\end{array}& for& \mathrm{\Delta }=1\\ 1mPas<\mu <1.2mPas& for& \mathrm{\Delta }<1\end{array}$

Ashgriz

Ashgriz 方法分离临界韦伯数的反射分离和聚结模态。

$${\text{We}}_d=\frac{f\left(\mathrm{\Delta }\right)}{{\mathrm{\Delta }}^6{\eta }_s+{\eta }_l}$$

(3158)

其中：

$$\begin{array}{c}{\eta }_s=2{(1-\xi )}^2{(1-{\xi }^2)}^{\frac{1}{2}}-1\\ {\eta }_l=2{(\mathrm{\Delta }-\xi )}^2{({\mathrm{\Delta }}^2-{\xi }^2)}^{\frac{1}{2}}-{\mathrm{\Delta }}^3\end{array}$$

(3159)

且 $\xi =\frac{1}{2}B(1+\mathrm{\Delta })$

$$f\left(\mathrm{\Delta }\right)=3\mathrm{\Delta }{(1+{\mathrm{\Delta }}^3)}^2[7{(1+{\mathrm{\Delta }}^3)}^{\frac{2}{3}}-4(1+{\mathrm{\Delta }}^2\left)\right]$$

(3160)

对于迎头碰撞 (B = 0)，临界韦伯数为 ${\text{We}}_d=\frac{f\left(\mathrm{\Delta }\right)}{{\mathrm{\Delta }}^3(1+{\mathrm{\Delta }}^3)}$ 。对于大小相等的液滴的迎头碰撞 ${\text{We}}_d=18.67$ 。该数值随着液滴尺寸差异的增加而增加。