Primary Atomization

LISA Model

The pressure-swirl atomizer, also commonly known as a simplex atomizer, is widely used for liquid-fuel injection in gas turbines, oil furnaces, and direct-injection spark-ignited automobile engines.

In this atomizer type, a swirling motion is imparted to the injected liquid through nozzles that are known as swirl ports. The liquid accelerates as it flows through the swirl ports into a central swirl chamber. Under the action of centrifugal force, it spreads out in the form of a conical sheet and develops a hollow air core. It emerges from the orifice as an unstable thinning liquid sheet, then breaking up into ligaments and then droplets. A sketch of a hollow-cone pressure swirl injector is shown in the figure below.

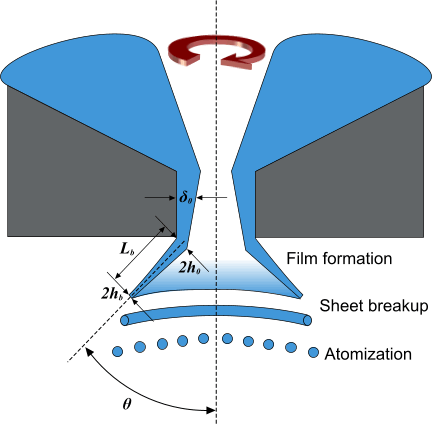
In the illustration above, three stages in the atomization process are identified: film formation, sheet breakup, and atomization. ${\delta }_o$ is the initial film thickness in the nozzle; $2h_0$ is the initial thickness of the film as it exits the nozzle, and $2h_b$ is the thickness of the film at the point of breakup. $\theta$ is the spray angle, which is defined as $0.5\times (\text{inner cone angle}+\text{outer cone angle})$ .

The LISA model that is implemented in Simcenter STAR-CCM+ is based primarily on the work of Senecal and others [702] and Schmidt and others [698].

Assumptions that are made in the LISA model are:

• A hollow-cone spray forms.
• The model only calculates a mean droplet diameter, and generates droplets at the injector position by assuming a Rosin-Rammler size distribution. The droplets are distributed uniformly in the spray cone.
• The primary breakup model does not operate in the spray region. The breakup length $L_b$ is assumed to be small, and the injection flow rate is steady. The atomized particles appear at the injection point immediately.
• Most numerical models assume that the slip velocity between the liquid sheet and the surrounding air is equal to the absolute velocity of the liquid near the injector ($v_s\equiv V_f$).

Film Formation

The centrifugal motion of the liquid within the injector creates a liquid film surrounding an air core. The thickness and velocity of the liquid film are calculated based on the input parameters for the pressure swirl injector. The initial sheet thickness within the injector, ${\delta }_0$, is

$${\dot{m}}_f=\pi \rho u_f{\delta }_0\left(d_0-{\delta }_o\right)$$

(3060)

where ${\dot{m}}_f$ is the mass flowrate through the injector (specified by you), $\rho$ is the density of the continuous phase, and $d_0$ is the injector exit diameter.

The axial component $u_f$ of the film velocity ${\mathbf{\text{v}}}_f$ at the injector exit is difficult to calculate from first principles. Instead, the approach from Han [662] is used. In this approach, the injector exit velocity profile is assumed to be uniform, and the absolute film velocity magnitude $V_f$ is related to the injection pressure head $\Delta p$ by:

$$V_f=\left|{\mathbf{\text{v}}}_f\right|=k_v\sqrt{\frac{2\Delta p}{\rho }}$$

(3061)

where ${\mathbf{\text{v}}}_f=u_f\mathbf{\text{i}}+v_f\mathbf{\text{j}}$

The value of the velocity coefficient $k_v$ is obtained [662] as

$$k_v=max[0.7,\frac{4\dot{m}}{\pi d_0^2{\rho }_f\cos \theta }\sqrt{\frac{{\rho }_f}{2\Delta p}}]$$

(3062)

The constant axial component is then

$$u_f=V_f\cos \theta$$

(3063)

where $\theta$ is the spray angle.

Sheet Breakup and Atomization

This section is only a brief summary of the breakup and atomization stage: details can be obtained from the paper by Senecal and others [702]. The model represents the film exiting the injector as a two-dimensional, viscous, incompressible liquid sheet of thickness $2h$ moving through a quiescent gas medium. The model also includes the effects of surrounding gas, liquid viscosity, and surface tension on the breakup of the liquid sheet. This phenomenon is depicted in the figure below.

Fluctuating velocities and pressure for both the liquid and the surrounding gas are produced by imposing a spectrum of infinitesimal wave-type disturbances on the initially steady motion. These disturbances, which are defined within a coordinate system that moves with the sheet, have the form:

$$\eta ={\eta }_0{e}^{(ikx+\omega t)}$$

(3064)

In this equation, ${\eta }_0$ is the initial wave amplitude, $k=2\pi /\lambda$ is the wavenumber, and $\omega ={\omega }_r+i{\omega }_i$ is the complex growth rate with $i$ being the imaginary unit ($i^2=-1$). The most unstable disturbance has the largest value of ${\omega }_r$, denoted by ${\Omega }_s$, and is assumed to be responsible for breakup. It is therefore desired to obtain a dispersion relation $\omega =\omega \left(k\right)$ from which the most unstable disturbance can be deduced. It has been shown that two solutions or modes exist that satisfy the conservation equations and their associated boundary conditions at the upper and lower interfaces for the disturbed liquid sheet. For the first solution, called the sinuous mode, the waves on the upper and lower boundaries are in phase. For the second solution, called the varicose mode, the waves are $\pi$ radians out of phase. Numerous authors (for example, Squire [707], Rangel and Sirignano [686], and Senecal and others [702]) have shown that the sinuous mode is dominant for low velocities and low gas to liquid density ratios. In addition, the modes become indistinguishable for high velocity flows.

As derived in Senecal and others [702], the dispersion relation for the sinuous mode is

$${\omega }^2[\tanh \left(kh\right)+\mathrm{\Gamma }]+\omega [4v_f{k}^2\tanh \left(\right(kh)+2i\mathrm{\Gamma }k{V}_s)]+4v_f^2{k}^4\tanh \left(kh\right)-4v_f^2{k}^3\xi \tanh \left(\xi h\right)-\mathrm{\Gamma }{V}_s^2{k}^2+\frac{\sigma k^3}{{\rho }_f}=0$$

(3065)

where $V_s$ is the magnitude of the relative velocity between the liquid film and the gas, $\Gamma =\rho /{\rho }_f$, $\xi =k^2+\omega /v_f$, and $\sigma$ is the surface tension.

With some simplifications, the growth rate for the sinuous mode is

$${\omega }_r=-\frac{2v_f{k}^2\tanh \left(kh\right)}{\tanh \left(kh\right)+\mathrm{\Gamma }}+\frac{\sqrt{4v_f^2{k}^4{\tanh }^2\left(kh\right)-{\mathrm{\Gamma }}^2{V}_s^2{k}^2-[\tanh \left(kh\right)+\mathrm{\Gamma }](-\mathrm{\Gamma }{V}_s^2{k}^2+\sigma k^3/{\rho }_f)}}{\tanh \left(kh\right)+\mathrm{\Gamma }}$$

(3066)

This expression can be simplified further depending on whether the disturbance waves being formed are long or short. The distinction between short or long waves is made by calculating the Weber number for the gas phase, $W{e}_g=\rho {V_s}^{2}h/\sigma$ (based on the relative liquid velocity, sheet half-thickness, and gas density). Short waves are formed for $W{e}_g>27/16$, corresponding to high-speed flows with $\rho /{\rho }_f«1$; otherwise long waves (corresponding to low-speed flows) are formed. Most modern injectors produce short waves.

Short Waves

For short waves the simplified expression for the growth rate is

$${\omega }_r=-2{\nu }_f{k}^2+\sqrt{4{{\nu }_f}^2{k}^4+\Gamma {V_s}^2{k}^2-\frac{\sigma k^3}{{\rho }_f}}$$

(3067)

Here, $k=K_s$ such that ${\omega }_r$ has its maximum value (denoted by ${\Omega }_s$). For this condition, the sheet breaks up at a length and time that are given, respectively, by

$$\begin{array}{c}{L}_b=V_f{\tau }_b\\ {\tau }_b=\frac{{\zeta }_b}{{\Omega }_s}\end{array}$$

(3068)

where ${\zeta }_b=\ln ({\eta }_b/{\eta }_0)$ is the sheet breakup empirical constant that you define (default value equal to 12). The ratio ${\eta }_b/{\eta }_0$ is the ratio of the surface disturbance at sheet breakup to the initial disturbance. The sheet half-thickness $h_b$ [686] at the breakup is

$$h_b=\frac{h_0\left(d_0-{\delta }_0\right)}{2L_b\sin \theta +d_0-{\delta }_0}$$

(3069)

where

$$h_0=0.5{\delta }_0\cos \theta$$

(3070)

The diameter of the ligament at sheet breakup is

$$d_L=\sqrt{\frac{16h_b}{K_s}}$$

(3071)

Long Waves

Viscosity has a minor effect on wave growth in the long wave regime. In this case, $K_s$ is directly obtained from an inviscid analysis as:

$$K_s=\frac{{\rho }_g{V_s}^2}{2\sigma }$$

(3072)

For the inviscid case:

$${\Omega }_s=\sqrt{\frac{\Gamma {V_s}^2{K_s}^2-\frac{\sigma {K_s}^3}{{\rho }_f}}{K_s{h}_b}}$$

(3073)

$$L_b=V_s{\tau }_b=\frac{V_s{\zeta }_b}{{\Omega }_s}$$

(3074)

Eqn. (3069), Eqn. (3073) and Eqn. (3074), determine the sheet half-thickness $h_b$ at the sheet breakup. The diameter of the ligament at sheet breakup is:

$$d_L=\sqrt{\frac{8h_b}{K_s}}$$

(3075)

Droplet Diameter Distribution

After calculating $d_L$, the mean diameter $d_D$ for the Rosin-Rammler distribution (with a spread parameter of 3.5 and a specified dispersion angle) is

$$d_D=1.88d_L{(1+3Oh)}^{1/6}$$

(3076)

where $Oh$, the Ohnesorge number, is

$$Oh=\frac{{\mu }_f}{{\left({\rho }_f\sigma d_L\right)}^{1/2}}$$

(3077)

Droplet Velocity Distribution

The initial velocity for each droplet is characterized by two angles: the polar angle ${\theta }_d$ and the azimuthal angle ${\alpha }_d$. The polar angle is based on the assumption of equal probability of velocity direction between the user-specified inner cone angle ${\theta }_i$ and outer cone angle ${\theta }_o$.

$${\theta }_d={\theta }_i+X_r({\theta }_o-{\theta }_i)$$

(3078)

where $X_r$ is a random number in the range [0, 1]. The azimuthal angle is taken as the user-specified swirl angle. Assuming that the magnitude of the droplet velocity at nozzle exit is the liquid film velocity $V_f$, the components of droplet velocity are calculated as:

$$\begin{array}{c}{v}_{d\mathrm{.}x}=V_f\sin \left({\theta }_d\right)\cos \left({\alpha }_d\right)\\ v_{d\mathrm{.}y}=V_f\sin \left({\theta }_d\right)\sin \left({\alpha }_d\right)\\ v_{d\mathrm{.}z}=V_f\cos \left({\theta }_d\right)\end{array}$$

Huh Model

Huh’s model is based on the premise, supported by order-of-magnitude estimates, that the two most important mechanisms in spray atomization are the gas inertia and the internal turbulence stresses generated in the nozzle [665].

The Huh model divides atomization into two stages:

1. The turbulence that is generated in the nozzle hole produces initial perturbations on the jet surface when it exits the hole.
2. Once the perturbations have reached a certain level, they grow exponentially by pressure forces. These forces are induced through interaction with the surrounding fluid (surface wave growth), until these perturbations become detached from the jet surface as droplets.

The model estimates the initial perturbations from an analysis of the flow through the hole and then uses established wave growth theory, together with other hypotheses, to represent the atomization process.

Following Huh, Lee, and Koo [666], an injected parcel bypasses the primary atomization stage if its Weber number is less than the user-specified Weber number ${\text{We}}_{\text{cr}}$. The Weber number is defined as:

where:

• ${\rho }_g$ is the density of the continuous phase.
• ${\mathbf{v}}_s$ is the relative velocity of the droplet in the continuum.
• $D_p$ is the droplet diameter.
• $\sigma$ is the surface tension.

Nozzle Turbulence and Its Decay

The average turbulence kinetic energy $k_a$ and its dissipation rate ${ϵ}_a$ at the hole exit are calculated from the following relations, which are derived from force and energy balances:

$$\begin{array}{ccc}{k}_a& =& \frac{U^2}{8\frac{L}{D}}(\frac{1}{c_d^2}-K_c-1)\hfill \\ {ϵ}_a& =& \frac{K_{ϵ}{U}^3}{2L}(\frac{1}{c_d^2}-K_c-1)\hfill \end{array}$$

(3080)

where:

• $U$ is the average injection velocity over the time period of injection.
• $L$ is the nozzle length, the length of the channel through the nozzle.
• $D$ is the nozzle diameter.
• $K_c$ is the form loss coefficient, default value 0.45. It is a proportionality constant for the pressure loss associated with the sharpness of the nozzle entrance corner.
  $$K_c=\frac{2\mathrm{\Delta }{p}_f}{\rho U^2}$$

  where:

  • $\mathrm{\Delta }{p}_f$ is the pressure loss across the nozzle corner.
  • $\rho$ is the density of the liquid.
• $K_{ϵ}$ is an empirical coefficient, default value 0.5, proportional to the initial dissipation rate of turbulent kinetic energy at the nozzle exit.
• $c_d$ is the nozzle discharge coefficient, default value is 0.6. It is a proportionality constant for the rate of volume flow through the nozzle.
  $$c_d=\frac{\dot{Q}}{A_0\sqrt{\frac{2\mathrm{\Delta }p}{\rho }}}$$

  where:

  • $A_0$ is the nozzle cross-section.
  • $\dot{Q}$ is the rate of volume flow.
  • $\mathrm{\Delta }p$ is the pressure drop across the nozzle.

If:

$$(\frac{1}{c_d^2}-K_c-1)\le 0$$

Eqn. (3080) simplifies to:

$$\begin{array}{ccc}{k}_a& =& \frac{1.5}{400}{U}^2\\ {ϵ}_a& =& C_{\mu }^{3/4}\frac{k_a^{3/2}}{0.01L}\end{array}$$

(3081)

The corresponding turbulence length scale $L_t^o$ and time scale ${\tau }_t^o$ are:

$$\begin{array}{ccc}{L}_t^o& =& C_{\mu }^{3/4}\frac{k_a^{3/2}}{{ϵ}_a}\\ {\tau }_t^o& =& C_{\mu }^{3/4}\frac{k_a}{{ϵ}_a}\end{array}$$

(3082)

where $C_{\mu }$ is the coefficient of the $k-ϵ$ model. Each injected (parent) droplet is assigned these scales as the initial values. Thereafter the turbulence within it decays with time. The following relations describe this time dependence:

$$L_t\left(t\right)=L_t^o{(1+C_{a1}\frac{t}{{\tau }_t^o})}^{C_{a2}}$$

(3083)

$${\tau }_t\left(t\right)={\tau }_t^o(1+C_{a1}\frac{t}{{\tau }_t^o})$$

(3084)

where $C_{a1}$ (default value 0.92) and $C_{a2}$ (default value 0.4565) are model coefficients.

Surface Wave Growth

The second stage of the atomization process is the interaction between liquid jet and surrounding gas field. This interaction increases the amplitude of the perturbation with wave growth rate $\mathrm{Re}\left[\omega \right]$ until these perturbations become detached from the jet surface ($\mathrm{Re}\left[\omega \right]$ is the real part of the complex wave celerity $\omega$. The value of $\mathrm{Re}\left[\omega \right]$ is equal to the reciprocal value of the wave growth time scale, ${\tau }_W$). These detached parts create the so-called ‘secondary droplets’. The perturbation amplitude obeys the dispersion equation, which is derived by Taylor [711]:

$${(\omega +2\nu {\kappa }^2)}^2+\frac{\sigma {\kappa }^3}{{\rho }_d}-4{\nu }^2{\kappa }^3{({\kappa }^2+\frac{\omega }{\nu })}^{1/2}+{(\omega +iU\kappa )}^2\frac{\rho }{{\rho }_d}=0$$

(3085)

where:

• $\sigma$ is the coefficient of surface tension.
• $\nu$ is the liquid kinematic viscosity.
• $\kappa =2\pi /L_W$ is the wavenumber.
  • $L_W=L_A/C_2$ is the wavelength of surface perturbation. $C_2$ is a model coefficient, default value 0.5.
  • $L_A=C_1{L}_t$ is the atomization length scale. $C_1$ is a model coefficient, default value 2.0.
• $\rho$ is the gas density.
• $i$ is the imaginary unit ($i^2=-1$).

The time scale of atomization ${\tau }_A$ is taken to be a linear combination of the turbulent time scale ${\tau }_t$ and the wave growth time scale ${\tau }_W$:

$${\tau }_A=C_3{\tau }_t+C_4{\tau }_W={\tau }_{spn}+{\tau }_{exp}$$

(3086)

where:

• ${\tau }_{spn}=C_3{\tau }_t$ is the spontaneous time scale; $C_3$ is a model coefficient, default value 1.0.
• ${\tau }_{exp}=C_4{\tau }_W$ is the exponential time scale; $C_4$ is a model coefficient, default value 1.5.

Droplet Size Distribution

This model assumes that droplets leave the nozzle with diameter $D_d$ then break up into secondary droplets. The break-up rate for droplets is:

$$\frac{d{D}_d}{dt}=-\frac{2L_A}{{\tau }_A{K}_A}$$

(3087)

where:

• $D_d$ is the diameter of the parent droplet.
• $K_A$ is a model constant to control the break-up rate, default value 0.1.

This initial break-up process stops when the spontaneous time scale becomes greater than the exponential scale.

The diameter of the secondary droplets that are formed from parent droplet break-up is estimated from the following probability density function:

$$f\left(x\right)=C\frac{\mathrm{\Phi }\left(x\right)}{{\tau }_A\left(x\right)}$$

(3088)

where:

• $x$ is droplet size.
• $C$ is a normalization constant.
• $\mathrm{\Phi }\left(x\right)$ is a dimensionless turbulence energy spectrum (assuming isotropic turbulence), estimated as:

  $$\mathrm{\Phi }\left(x\right)=\frac{{\left(\kappa \left(x\right)/{\kappa }_e\right)}^2}{{(1+{\left(\kappa \left(x\right)/{\kappa }_e\right)}^2)}^{11/6}}$$

  (3089)

  where ${\kappa }_e=2\pi /L_e$, and $L_e=L_t/0.75$ with $L_t$ being the turbulence length scale.

The distribution function for droplet diameters, $F\left(x\right)$, is then:

$$F\left(x\right)={\int }_{x_{\min }}^{x}f\left(x\right)dx$$

(3090)

$x_{\min }$ is the minimum droplet size, which is calculated from Kelvin-Helmholtz instability theory as:

$$x_{\min }=2\pi \frac{{\sigma }_d({\rho }_d+\rho )}{U^2{\rho }_d\rho }$$

(3091)

where:

• ${\sigma }_d$ is the surface tension of the droplet.
• ${\rho }_d$ is the density of the droplet.
• $\rho$ is the density of the gas.

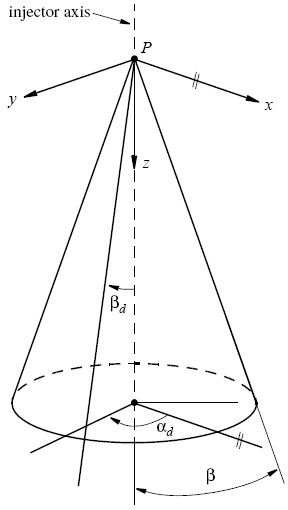
Spray Angle and Initial Velocity

The spray semi-cone angle $\beta$ is calculated from:

$$\tan \left(\beta \right)=\frac{L_A/{\tau }_A}{U}$$

(3092)

where ${\tau }_A$ is the breakup time.

$\beta$ determines the upper limit of the initial radial droplet velocity component. The estimation of initial velocity for each droplet is based on the assumption of equal probability of velocity direction within a spray cone. The components of droplet velocity $v_d$ are calculated as:

$$v_{d,x}=v_d\sin \left({\beta }_d\right)\cos \left({\alpha }_d\right)$$

$$v_{d,y}=v_d\sin \left({\beta }_d\right)\sin \left({\alpha }_d\right)$$

$$v_{d,zy}=v_d\cos \left({\beta }_d\right)$$

where ${\beta }_d$ and ${\alpha }_d$ are randomized angles that are given by:

$${\beta }_d=X_{r,1}\beta$$

$${\alpha }_d=2\pi X_{r,2}$$

where $X_{r,1}$ and $X_{r,2}$ are random numbers in the range [0, 1].