TAB 变形和破碎模型

泰勒模拟破碎 (TAB) 模型基于泰勒模拟。该模拟将变形液滴表示为阻尼弹簧-质量系统；它仅考虑液滴振荡的基本模式。弹簧-质量系统中质量的位移和速度对应于液滴的代表性变形和变形率物理量。

TAB 模型方程控制液滴振荡和变形 [680]。当液滴振荡达到临界值时，破碎使用子颗粒替换父颗粒，该子颗粒的直径可从 Rosin-Rammler 分布中选择。默认情况下，破碎过程不会创建粒子束。原始粒子束将会保留，但颗粒直径将更改为新子值。不过，可以选择创建新的粒子束。在这种情况下，可以单独选择液滴直径。对通过破碎生成的液滴大小分布进行建模时，此功能十分有用。破碎过程中涉及的粒子束的横向速度需与破碎时的液滴振荡动能成比例。该速度易于从喷射器生成扩散效应。从某种程度上来说，不需要锥喷射器。

尽管 TAB 模型基于振动流态中的单振荡模式，但在低和高韦伯数限制中，它可再现与 Reitz-Diwakar 模型相同的特征时间尺度。不过，TAB 模型通常在低韦伯数下使用。例如，空心锥汽油喷射便是此模型的首选应用示例 [647]。超过其有效范围时，该模型容易低估液滴大小。

液滴变形

TAB 变形模型的目的是根据其平衡位置计算液滴赤道的瞬时位移 x。

下图显示了此位移（在 Baumgarten [647] 之后）。

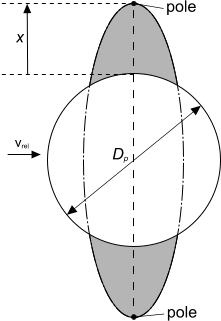
为了简化分析，此位移将标准化为液滴直径

图 1. EQUATION_DISPLAY

y = \frac{2 x}{C_{b} D_{p}}

(3110)

其中， $C_{b}$ 为经验常数。变形液滴和阻尼弹簧-质量系统之间的泰勒模拟 [711] 给出控制 y 的二阶常微分方程

图 2. EQUATION_DISPLAY

\frac{ρ_{l} D_{p}^{2} \ddot{y}}{4} = \frac{C_{k} σ}{D_{p}} (\frac{W e}{W e_{c r i t}} - 2 y) - C_{d} μ_{l} \dot{y}

(3111)

其中，

σ

和

μ_{l}

分别为液滴的表面张力和粘度，

W e

为其韦伯数 Eqn. (3093)。

C_{d}

、

C_{k}

和

W e_{c r i t}

分别是默认值为 5、8 和 12 的经验常数。

C_{b}

不会出现在 Eqn. (3111) 中：它不是确定 y 必需的参数。为喷射的每个液滴对 Eqn. (3111) 进行积分，初始条件为

y = \dot{y} = 0

。

液滴破碎

TAB 破碎模型依赖 TAB 变形模型计算标准化液滴变形 y。

当 y 达到 1 (Eqn. (3110)) 时，假设液滴严重变形，然后触发破碎过程。根据能量平衡 [680]，破碎后液滴的 Sauter 平均直径 $D_{32}$ 与父液滴的直径 $D_{p}$ 相关，得出以下公式

图 3. EQUATION_DISPLAY

\frac{D_{p}}{D_{32}} = 1 + \frac{K C_{b}^{2} C_{k}}{5} + \frac{3 C_{b}^{2} m_{p}}{4 σ π} (\frac{K}{5} - \frac{C_{v}^{2}}{6}) {\dot{y}}^{2}

(3112)

此处， $C_{k}$ 和 $C_{b}$ 从 TAB 变形模型继承，其中， $C_{b}$ 采用默认值 0.5。 $K$ 是变形和振荡中的总能量与基本模式下的能量之比，默认值为 10/3。在 Simcenter STAR-CCM+ 中，通过使用 Sauter 平均直径（由 Eqn. (3112) 给出）和用户指定的指数（扩散）对 Rosin-Rammler 分布进行采样，可得出子液滴的直径。此操作针对父粒子束和（可选）每个子粒子束单独完成。

破碎后粒子束的速度还垂直于父粒子束的原始速度。这与破碎时的变形率 ${\dot{y}}_{b}$ 成比例

图 4. EQUATION_DISPLAY

v_{⊥} = \frac{1}{2} C_{v} C_{b} D_{p} {\dot{y}}_{b}

(3113)

在 Eqn. (3112) 和 Eqn. (3113) 中， $C_{v}$ 为法向速度系数。可以调整此系数来生成已知的喷射角度；或者，可以直接在锥喷射器上指定喷射角度，在这种情况下， $C_{v}$ 应设为零。