壁面碰撞

Bai-Gosman 壁面碰撞

Bai-Gosman 模型最初在 [648]、[649] 和 [650] 中描述，但已针对 Simcenter STAR-CCM+ 进行扩展，将可能的结果分类为六种可能流态中的某个，如下图所示。

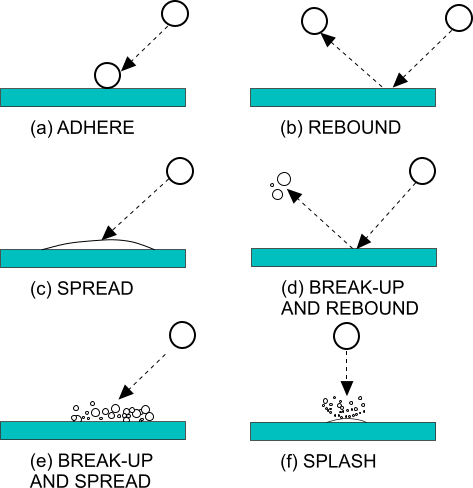
对于液膜边界，液滴损失的动量和动能被液膜获取。

可使用以下四个参数为给定碰撞事件选择流态：

• 入射韦伯数

  $$W{e}_I=\frac{{\rho }_p{v}_{r,n}^2{D}_p}{\sigma }$$

  (3177)

  其中， $v_{r,n}=\left({\mathbf{\text{v}}}_p-{\mathbf{\text{v}}}_w\right)\cdot {\mathbf{\text{n}}}_w$ 为颗粒速度相对于壁面的法向分量。 ${\mathbf{\text{n}}}_w$ 为垂直于边界的单位矢量。

• Laplace 数

  $$\text{La}=\frac{{\rho }_p\sigma D_p}{{\mu }_p^2}$$

  (3178)
• 边界温度 $T_w$ （假设能量模型在物理连续体中处于活动状态）。
• 壁面状态；边界可以是湿的或干的。对于液膜边界，这取决于液膜是否存在。对于其他边界，这取决于用户选定的“壁面状态”属性。

  对于干燥壁面状态：

  • 当韦伯数小于 ${We}_c$ 且壁面温度小于 $T_{12}$ 时，碰撞液滴会在壁面上扩散。

  • 当韦伯数或壁面温度较高时，液滴可能扩散、破碎且扩散、破碎且反弹或者反弹。

  • 大于 ${We}_c$ 时，碰撞液滴将飞溅。

  对于湿壁面状态：

  • 当韦伯数小于 2 且壁面温度小于 $T_{12}$ 时，碰撞液滴将粘附在壁面上。

  • 当韦伯数或壁面温度较高时，液滴可能扩散、破碎且扩散、破碎且反弹或者反弹。

  • 大于 ${We}_c$ 时，碰撞液滴将飞溅。

当温度足够高（在 $T_{12}$ 处）时，会发生莱登弗洛斯特效应，并且摩擦和热传递减小。其峰值出现在 $T_{23}$ 处。

流态转变条件

下面显示了碰撞流态的理想化图，其中存在由两个转变温度分隔的三个温度范围：

• $T_{12}$ 分隔范围 1 与范围 2，预期与液滴的沸腾温度接近。
• $T_{23}$ 分隔范围 2 与范围 3，预期与液滴的莱登弗洛斯特温度接近。

下面给出了三个壁面温度范围内湿壁面的转变条件。

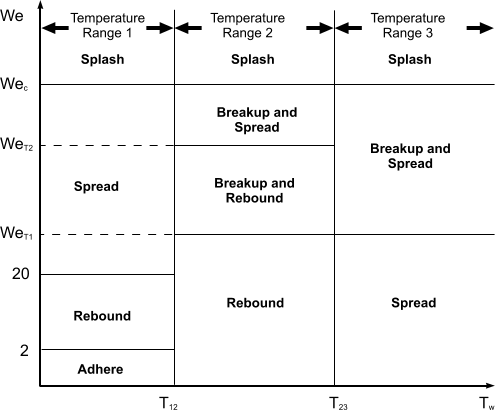
可在此模型的专家属性中调整上图中显示的韦伯数 2 和 20。

以下为三个壁面温度范围内干燥壁面的转变条件。

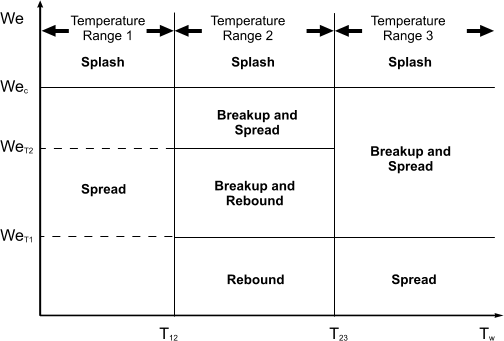
温度范围 1

第一个温度范围表示为：

$$T_w\le T_{12}$$

(3179)

它也适用于能量模型在物理连续体中未激活的情况。在此温度范围内，该模型可识别以下流态：

• 粘附

  $$W{e}_I\le 2$$

  (3180)

  碰撞液滴以接近球体的形状粘附在边界上。如果边界为液膜，则液滴会将其质量、动量和动能传递给液膜。

  Simcenter STAR-CCM+ 支持使用特定的边界相互作用模式，以控制满足粘附条件的颗粒的结果。在非稳态条件下，默认设置为“粘附”；而在稳态条件下，默认设置为 Escape(逃逸)。

• 反弹

  $$W{e}_I\le 20$$

  (3181)

  碰撞液滴在冲击后从边界反弹回来。这在功能上与具有恢复系数的反弹边界相互作用模式相同

  $$e_n=0.993-1.76\theta +1.56{\theta }^2-0.49{\theta }^3$$

  (3182)

  $$e_t=\frac{5}{7}$$

  (3183)

  其中， $\theta$ 为从边界测量的液滴入射角。

• 扩散

  $$W{e}_I\le W{e}_c$$

  (3184)

  液滴在湿边界上与现有液膜融合。如果边界为液膜，则液滴会将其质量、动量和动能传递给液膜。限制韦伯数 $W{e}_c$ 由以下公式给出

  $${\text{We}}_c=A{\text{La}}^{-0.18}$$

  (3185)

  对于光滑壁面或湿粗糙壁面

  $$A=A_w$$

  (3186)

  其中， $A_w$ 为用户自定义飞溅开始系数，默认值为 1320。

  对于干粗糙壁面， $A$ 从下表插值

  粗糙度 $\text{μ}\text{m}$	0	0.05	0.14	0.84	3.1	12.0	$\infty$
  $\mathbf{\text{A}}/{\mathbf{\text{A}}}_{\mathbf{\text{w}}}$	3.9879	3.9879	3.4348	1.9955	1.5576	1.0015	1

  如果存在可以形成液膜的液膜边界，则温度范围 1 的扩散区中发现的粒子束会将其质量、动量和能量传递至液膜。如果没有液膜边界，因此无法形成液膜，则扩散区中的粒子束会反弹，其法向复原系数为 0 ( $e_n=0$ ) 和切向复原系数为 1 ( $e_t=1$ )。

• 飞溅

  $$W{e}_I>W{e}_c$$

  (3187)

  碰撞液滴会破碎成更小的液滴，其中一些会从边界反射回来。残留物可能粘附在壁面上。质量为 $m_{\pi }$ 的每个碰撞粒子束会产生在喷射锥角内从壁面随机反射的用户指定数量的二次粒子束。二次粒子束的总质量 $m_s$ 通过以下飞溅质量比率确定：

  $$r_m=\frac{m_s}{m_{\pi }}=C_b+\left(\begin{array}{c}{C}_{rd}\\ C_{rw}\end{array}\right)X_r$$

  (3188)

  其中：

  • $C_b$ 为基础系数。
  • $C_{rd}$ 为干燥壁面的范围系数。
  • $C_{rw}$ 为湿润壁面的范围系数。
  • $X_r$ 为在 [0 — 1] 范围内均匀分布的随机数字。

  每次飞溅形成的二次液滴总数如下

  $$N_s=a_0\left(\frac{W{e}_I}{W{e}_m}-1\right)$$

  (3189)

  其中：

  • $a_0$ 为用户指定的系数（默认值为 5）
  • $W{e}_m$ 为韦伯数，在此温度范围内，等于 $W{e}_c$ 。

  由于二次粒子束的数量倾向于无穷，因此飞溅事件形成的二次液滴的实际数量倾向于 $N_s$ 。要确保这一点，可从具有用户指定指数 $q$ 和参考直径的 Rosin-Rammler 分布中随机选择每粒子束中二次液滴的直径和数量

  $$D_{ref}={\left(\frac{r_m}{N_s\Gamma (1+3/q)}\right)}^{1/3}{D}_p$$

  (3190)

  其中， $\Gamma \left(x\right)$ 为 gamma 函数。默认指数 $q=1$ 将生成卡方分布。

  二次液滴的速度计算基于两个贡献；一个是法向入射分量 ${\mathbf{\text{v}}}_n$ 所做的贡献，另一个是切向入射分量 ${\mathbf{\text{v}}}_t$ 所做的贡献。二者分别以 ${{\mathbf{v}}^{\prime }}_n$ 和 ${{\mathbf{\text{v}}}^{\prime }}_t$ 表示。

  每个二次粒子束的 ${{\mathbf{\text{v}}}^{\prime }}_n$ 的幅值的计算基于总体能量守恒，如 [650] 所述。选取 ${{\mathbf{\text{v}}}^{\prime }}_n$ 的方向的方法为，在范围 [0°, 360°] 内随机选择方位角，以及在用户指定范围（默认为 [5°, 50°]）内选择相对于壁面的喷射角。

  如果能量不足以为所提的二次粒子束提供表面能量和动能，则不会发生飞溅。相反，碰撞液滴仅发生扩散。

  ${\mathbf{\text{v}}}_t$ 分量对二次液滴速度的直接贡献如下

  $${{\mathbf{\text{v}}}^{\prime }}_t=c_f{\mathbf{\text{v}}}_t$$

  (3191)

  其中， $c_f$ 为壁面摩擦系数，估计范围介于 0.6 到 0.8 之间；默认值设为 0.7。

  最后，父粒子束将粘附在壁面上。其质量将按因子 $\left(1-r_m\right)$ 减小，而其表示的液滴数保持不变。

温度范围 2

第二个温度范围表示为：

$$T_{12}<T_w\le T_{23}$$

(3192)

在此范围内，由于介于中间的蒸汽液膜，因此不会发生任何接触或沉积。流态取决于两个特征韦伯数 ${\text{We}}_{T1}$ 和 ${\text{We}}_{T2}$ ，如下所示：

• 反弹：

  $${\text{We}}_I\le {\text{We}}_{T1}$$

  (3193)
• 破碎且反弹：

  $${\text{We}}_{T1}<{\text{We}}_I\le {\text{We}}_{T2}$$

  (3194)

  入射液滴将破碎并从壁面反弹回来。此流态实施为第一个温度范围内飞溅流态的变体，唯一不同的是壁面上没有留下任何残留物 ( $r_m=1$ )， ${\text{We}}_m={\text{We}}_{T1}$ 。

• 破碎且扩散：

  $${\text{We}}_{T2}<{\text{We}}_I\le {\text{We}}_c$$

  (3195)

  入射液滴将破碎并沿壁面扩散。此流态实施为第一个温度范围内飞溅流态的变体，唯一不同的是壁面上没有留下任何残留物 ( $r_m=1$ )， ${\text{We}}_m={\text{We}}_{T2}$ ，喷射角为零。

• 飞溅：

  $${\text{We}}_I>{\text{We}}_c$$

  (3196)

  与第一个温度范围内的飞溅流态相同，唯一不同的是壁面上没有留下任何残留物 ( $r_m=1$ )。

根据 [648]，对于水， ${\text{We}}_{T1}$ 和 ${\text{We}}_{T2}$ 分别采用默认值 30 和 80。

温度范围 3

第三个温度范围表示为：

$$T_w>T_{23}$$

(3197)

同样，蒸汽液膜阻碍了壁面接触，液滴从表面升高并沿表面的切线方向移动。流态如下

• 扩散：

  $${\text{We}}_I\le {\text{We}}_{T1}$$

  (3198)
• 破碎且扩散：

  $${\text{We}}_{T1}<{\text{We}}_I\le {\text{We}}_c$$

  (3199)

  入射液滴将破碎并沿壁面扩散。此流态实施为第一个温度范围内飞溅流态的变体，唯一不同的是壁面上没有留下任何残留物 ( $r_m=1$ )， ${\text{We}}_m={\text{We}}_{T1}$ ，喷射角为零。

• 飞溅：

  $${\text{We}}_I>{\text{We}}_c$$

  (3200)

  与第一个温度范围内的飞溅流态相同，唯一不同的是壁面上没有留下任何残留物 ( $r_m=1$ )。

Bai-ONERA 壁面碰撞

Bai-ONERA 模型是根据 Bai-Gosman 模型开发的。此模型专门用于实现平滑过渡，从而在壁面温度低于液滴饱和温度的情况下恢复 Bai-Gosman 模型。它可预测液滴冲击壁面的结果，并特别注意了壁面温度介于液体的沸点和莱登弗洛斯特点之间时的结果。

Bai-ONERA 模型将可能的结果分类为四种可能流态中的某个，如下图所示。

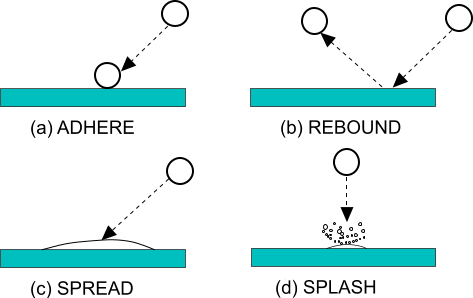
对于液膜边界（湿壁面），液滴损失的动量和动能将传递到液膜。

可使用以下三个参数为给定碰撞事件选择流态：

• 无量纲温度 $T^{*}$ is defined as:
  $$T^{*}=\frac{T_w-T_s}{T_L-T_s}$$
  其中：

  • $T_w$ 为壁面温度
  • $T_s$ 为饱和温度
  • $T_L$ 为莱登弗洛斯特温度
• 液滴韦伯数 $We$ ，基于壁面与液滴之间的相对速度的法向分量（请参见 Eqn. (3177)）。
• Ohnesorge 数 $Oh$ ，定义如下：
  $$Oh=\frac{{\mu }_p}{\sqrt{{\rho }_p\sigma D_p}}=\frac{1}{\sqrt{La}}$$
  其中， $La$ 为 Laplace 数（请参见 Eqn. (3178)）。

Weber 和 Ohnesorge 数可组合成一个无量纲参数 $K$ ，定义如下

流态转变条件

碰撞流态的映射图（如下所示）分为由两个转变温度分隔的三个温度范围：

• $T_{12}$ ，分隔范围 1 与 2，预期近似等于饱和温度 $T_s$ 。
• $T_{23}$ ，分隔范围 2 与 3，预期近似等于莱登弗洛斯特温度 $T_L$ 。

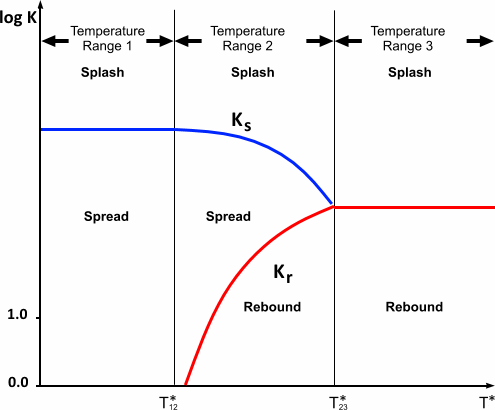
原始 ONERA 模型的冲击结果映射显示在下面的对数 K-T* 绘图中。飞溅和扩散之间的转换为函数 $K_s$ ：

$$K_s\left(T^{*}\right)=\{\begin{array}{ccc}{K}_0\hfill & ;& T^{*}\le 0,T_w\le T_{12}\\ K_0+T^{*}(K_1-K_0)\hfill & ;& 0<T^{*}<1,T_{12}<T_w<T_{23}\\ K_1\hfill & ;& 1\le T^{*},T_{23}\le T_w\end{array}$$

(3202)

扩散与反弹之间的转换为函数 $K_r$ ：

$$K_r\left(T^{*}\right)=\{\begin{array}{ccc}0\hfill & ;& T^{*}\le 0,T_w\le T_{12}\\ K_1{\cdot \left(T^{*}\right)}^{\gamma }\hfill & ;& 0<T^{*}<1,T_{12}<T_w<T_{23}\\ K_1\hfill & ;& 1\le T^{*},T_{23}\le T_w\end{array}$$

(3203)

原始 ONERA 模型中有三个模型系数（ $K_0$ 、 $K_1$ 和 $\gamma$ ）。Simcenter STAR-CCM+ 中实施的 Bai-ONERA 模型可以平滑过渡到温度范围 1 中的 Bai-Gosman 模型，因此 $K_0$ 的值由 Bai-Gosman 模型的扩散-飞溅转换条件在内部确定。 $K_1$ 和 $\gamma$ 均为模型常数，默认值分别为 450 和 3。

光滑的干燥壁面

对于光滑的干燥壁面：

• $K_1=450$ 。
• $\gamma =3$ 。

粗糙的干燥壁面

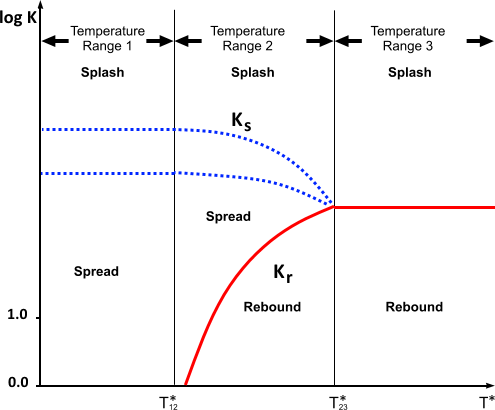
对于温度范围 1 中的粗糙干燥壁面， $K_0={We}_A{Oh}^{-0.4}$ ，其中， ${We}_A=A{La}^{-0.18}$ 。系数 $A$ 取自下表：

壁面粗糙度	0.05 µm	0.14 µm	0.84 µm	3.1 µm	12.0 µm
系数 A	5264	4534	2634	2056	1322

因此，转换 $K_s$ 发生于下图中的两条虚线之间，确切位置取决于壁面粗糙度。

湿壁面

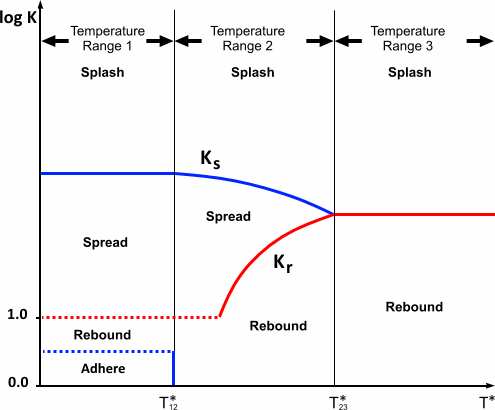
对于温度范围 1 中的湿壁面， $K_r\le 20.0{La}^{0.20}$ 用于分隔反弹与扩散流态，如下图中的虚线所示。线的实际位置取决于给定液滴的 Laplace 数 $La$ 。虚线将延长到温度范围 2 中，直到其与 Eqn. (3203) 中定义的 $K_r$ 函数合并。

此外，为保持与 Bai-Gosman 模型的兼容性，Bai-ONERA 模型包含一个粘附流态，适用于在温度范围 1 内具有较低冲击韦伯数的液滴。

飞溅比

飞溅比 $r_s$ 是飞溅液滴质量与入射液滴质量之比：

$$r_s=\frac{m_s}{m_i}$$

(3204)

其中， $m_s$ 为飞溅质量， $m_i$ 为入射质量。

在表面上扩散的液滴质量为 $m_{spr}=m_i-m_s=(1-r_s)m_i$ 。

要调整 $r_s$ 以反应大于莱登弗洛斯特温度时没有扩散这一事实，需要引入具有以下特性的校正因子 $f\left(T^{*}\right)$ ：

• $m_{spr}=(1-r_s)m_{i}f\left(T^{*}\right)$ 。
• $f$ 为单调。
• $f=1$ 时， $T^{*}=0(=T_{12}^{*})$ 。
• $f=0$ 时， $T^{*}=1(=T_{23}^{*})$ 。

$f$ 定义如下：

$$\begin{array}{c}\\ \begin{array}{c}f\left(T^{*}\right)\\ \end{array}\end{array}=\{\begin{array}{ccc}1.0& ;& T^{*}\le 0,T\le T_{12}\\ 1-{\left(T^{*}\right)}^n& ;& 0<T^{*}<1,T_{12}<T<T_{23}\\ 0.0& ;& 1\le T^{*},T_{23}\le T\end{array}$$

(3205)

其中， $n$ 为 Bai-ONERA 模型的 Smrf 属性，用于控制变体的形状。

则，飞溅质量如下：

$$m_s=m_i[1-(1-r_s)f\left(T^{*}\right)]$$

(3206)

Satoh 壁面碰撞模型

Satoh 模型用于预测冲击固体边界的油滴的结果，尤其是在油雾隔离膜中。

在 Satoh 模型 [695] 中，假设碰撞边界的液滴会发生回弹或扩散，具体取决于其直径 $D$ 以及垂直于壁面的速度 $Vp$ 。

同时发生反弹和扩散的中间区域定义在两条线之间，即初始扩散线 (ISL) 和充分扩散线 (FSL)。这两条线均遵循幂次定律曲线。

• 初始扩散线

  $${Vp}_{\text{ISL}}=a_{\text{ISL}}{\left(\frac{D}{D_{\text{ref}}}\right)}^{n_{\text{ISL}}}$$

  (3207)
• 充分扩散线

  $${Vp}_{\text{FSL}}=a_{\text{FSL}}{\left(\frac{D}{D_{\text{ref}}}\right)}^{n_{\text{FSL}}}$$

  (3208)

其中， $D_{\text{ref}}$ 为参考直径， $a$ 为指前乘数， $n$ 为指数值。

根据 Satoh 和其他作者的文章 [695]，颗粒直径及其边界法向速度可确定颗粒与边界之间的碰撞结果。假设两者之间的关系符合以下描绘的两条幂次定律曲线。在称为初始扩展线的下部曲线下方，所有颗粒均反弹。在称为充分扩展线的上部曲线上方，颗粒在边界上扩散。在两条曲线之间的区域中，一些颗粒反弹，而其余的颗粒扩散。

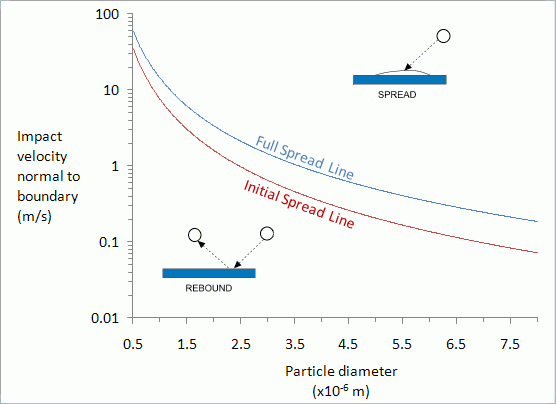
液滴直径在 0 m 到 8E-6 m 的范围内。液滴的壁面法向碰撞速度在 0.01 m/s 到 13 m/s 的范围内。在此范围内，具有较慢法向速度的小液滴从壁面反弹，而具有较快法向速度的大液滴趋向于在表面上扩散，以形成液膜。

在 Simcenter STAR-CCM+ 中，液膜的形成取决于模型选择和边界类型。将使用优先顺序对扩散行为建模：如果液膜模型不可用，则使用粘附模式。如果两种模式都不适用于入射边界，则颗粒可以退出。

反弹

反弹模式仅适用于壁面、挡板和接触界面。反弹颗粒在模拟中保持活动状态；该模式以其对颗粒速度的处理方式而与众不同。相对于壁面速度的反弹速度取决于碰撞速度和用户自定义的恢复系数：

上标 R 和 I 分别表示反弹和碰撞；下标 n 和 t 分别表示壁面法向和切向。由于 Eqn. (3209) 的左侧可拆分成正交 n 和 t 分量，因此可分成两个方程：

用于强调恢复系数的定义是碰撞和反弹速度之间的比例常数。这两个系数的范围都介于 0 到 1 之间。后者“理想”弹性反弹为默认值。

壁面边界的切向速度为零，除非通过壁面滑移选项显式指定一个值。换言之，它仅在无滑移壁面处不为零。

飞溅

飞溅模式仅适用于液滴和固体壁面。在此模式下，液滴会碰撞固体或润湿表面，并破碎成多个反弹液滴。

飞溅颗粒速度的幅值由速度比率及其方向、飞溅角 $\alpha$ 和切向速度比率 $R_t$ 定义。

如果切向速度比率 $R_t$ = 0 或碰撞速度垂直于表面，则飞溅颗粒的方向在圆锥表面上随机选择。

飞溅角 $\alpha$ 定义半锥角，且冲击时圆锥轴垂直于表面。

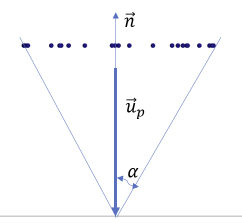
如果比率为正，则圆锥轴在碰撞速度的相切分量 $u_{p,t}$ 的方向上倾斜。

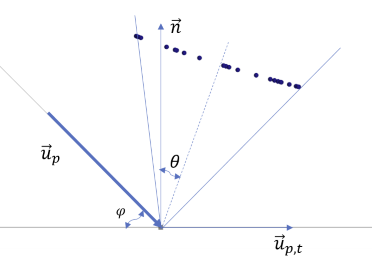
倾角 $\theta$ 取决于切向速度比率 $R_t$ 、碰撞角 $\phi$ 和飞溅角 $\alpha$ ：

碰撞热传递

碰撞热传递模型设计用于预测壁面与碰撞该壁面的液滴流之间的热传递。在具有双向耦合的模拟中，液滴可能改变壁面的温度。

即使在壁面温度高于莱登弗洛斯特温度的情况下，也会发生此温度变化。液滴与壁面之间的热传递可通过气相进行，尽管这样比没有莱登弗洛斯特效应时的速度更慢。之后，液滴可将壁面温度降低到莱登弗洛斯特点之下，以便能够形成液膜。

该模型采用如下假设：

• 能量从液滴流向壁面时通过的面积不大于壁面的面积。
• 对于温度固定的壁面边界条件（单向耦合），热传递由颗粒温度和壁面温度之差驱动。单向耦合中的导热率就是液滴材料的导热率。
• 液滴在冲击过程中变形，并将其有效直径增加到由 Eqn. (3216) 所给出的数量，由此计算有效面积。
• 假设采用扩散喷射。
• 如果面上的液膜厚度大于 1E-8 米，液滴会被直接吸收到液膜中。

在高质量负载（例如，体积分数大于 0.3 时）下，这些假设可能不成立，从而导致气相中出现奇怪的行为。此类行为包括但并不限于，虚假的温度波动、不实际的颗粒温度和常规收敛困难。

方程 Eqn. (3221) 中固体壁面的热穿透系数 $b_w$ 可乘以 HPC 乘数。在使用常数、场函数或表方法的瞬态模拟中，这可用于对壁面中的涂层或阻力进行建模。

液滴或颗粒的能量方程如下：

其中：

• ${\dot{Q}}_c$ 为对流的热传递速率。
• ${\dot{Q}}_r$ 为辐射的热传递速率。
• ${\dot{Q}}_l$ 为质量传递的热传递速率。
• ${\dot{Q}}_s$ 为用户自定义热源的热传递速率。
• ${\dot{Q}}_{wp}$ 为壁面传导的热传递速率。

从壁面到液滴的热传递通过 Wruck 相关性 [714] 描述：

其中，带 $w$ 或 $p$ 的术语指壁面或颗粒， $\Delta t_p$ 为颗粒时间步。

其中， $D_{\text{eff}}$ 是整个液滴接触时间内的时间平均有效直径（Akao 等人提出的[642]）：

其中， $D_0$ 为液滴直径， ${We}_p$ 为液滴韦伯数。

接触时间

$t_{\text{cont}}$ 为颗粒与壁面的接触时间。

$$t_{\text{cont}}=\{\begin{array}{cc}\frac{\pi }{4}\sqrt{\frac{{\rho }_p{D_0}^3}{{\sigma }_p}}& K<40\\ \sqrt{\frac{\pi }{2}}{\left(\frac{{\rho }_p{D_0}^5}{{\sigma }_p{u_r}^2}\right)}^{0.25}& K\ge 40\end{array}$$

(3217)

其中：

• ${\rho }_p$ 为颗粒密度。
• ${\sigma }_p$ 为颗粒表面张力。
• $u_r$ 为颗粒相对于壁面的速度。
• $K$ 为与冲击能成比例的无量纲数。根据 Birkhold 等人的[652]，此数定义如下：

  $K={Ca}^{5/4}{La}^{3/4}$

  其中， $Ca$ 为毛细管数， $La$ 为 Laplace 数。

以下方法可用于计算接触时间：

Aiko

$$t_{\text{cont}}^{\text{Aiko}}=A{t}_{\text{cont}}$$

(3218)

其中， $A$ 为常数。这是默认设置。

Birkhold

此方法考虑沸腾对液滴与壁面之间热传递的影响。开始沸腾后，液滴和壁面之间不再存在接触。Birkhold 方法引入了沸腾延迟时间：

$$t_s=AT+B$$

(3219)

其中 $A$ 和 $B$ 是经验常数，具体取决于壁面和液滴 [652] 的材料。 $t_s$ 应随着壁面温度的增加而减小。（壁面温度越高，沸腾发生得越快。）

接触时间的计算如下：

$$t_{\text{cont}}^{\text{Birkhold}}=\text{min}(t_{\text{cont}},t_s)$$

(3220)

热穿透系数

$b_w$ 和 $b_p$ 是根据壁面或颗粒的材料计算的热穿透系数。

$$\begin{array}{cc}{b}_w=c_h\sqrt{{\kappa }_w{\rho }_w{\left(C_p\right)}_w}\text{,}& b_p=\sqrt{{\kappa }_p{\rho }_p{\left(C_p\right)}_p}\end{array}$$

(3221)

其中：

• $c_h$ 为 HPC 乘数（默认值为 1.0），用于表示涂层或其他热阻。
• ${\kappa }_w$ 和 ${\kappa }_p$ 分别为壁面和颗粒的导热率。
• ${\rho }_w$ 和 ${\rho }_p$ 分别为壁面和颗粒的密度。
• ${\left(C_p\right)}_w$ 和 ${\left(C_p\right)}_p$ 分别为壁面和颗粒的比热。

如果没有导热固体，则使用壁面温度来计算具有 Wruck 相关性的热通量。由于没有为壁面指定材料， $b_w$ 设为非常大的数字，将调和平均数降低到 $b_p$ 。

壁面和液滴温度

$T_w$ 和 $T_p$ 分别为壁面和液滴的温度。

Eqn. (3214) 可以写为：

$${\dot{Q}}_{wp}=A_p{h}_{wp}\left(T_w-T_p\right)$$

(3222)

其中：

• $A_p$ 为颗粒的横截面积。
• $h_{wp}$ 为：

  $$h_{wp}=\frac{2A_{\text{cont}}\sqrt{t_{\text{cont}}}\left(b_w{b}_p\right)}{A_p\sqrt{\pi }(b_w+b_p)\Delta t_p}$$

  (3223)

液膜阻尼

当固体颗粒通过液膜时，液膜阻尼模式可在它们碰撞壁面前后立即对其运动进行阻尼衰减。此模式仅适用于液膜边界上的固体颗粒。

在这种情况下，假设材料颗粒的动量守恒方程简化为：

其中：

• ${\mathbf{\text{F}}}_d$ 为曳力
• ${\mathbf{\text{F}}}_{vm}$ 为虚拟质量力

曳力

可以使用标准形式的曳力方程。由于颗粒为球形小固体颗粒，因此可以使用 Schiller-Naumann 相关性计算颗粒的曳力系数 $C_d$ 。

虚拟质量力

可使用两个假设简化虚拟质量力方程：

• 虚拟质量系数 $C_{vm}$ 等于 0.5
• 与颗粒加速度相比，液膜的加速度可忽略不计：

$$\left|\frac{D\mathbf{\text{v}}}{Dt}\right|«\left|\frac{d{\mathbf{\text{v}}}_p}{dt}\right|$$

(3225)

使用这些假设后，虚拟质量力变为：

$${\mathbf{\text{F}}}_{vm}=-0.5\rho V_p\frac{d{\mathbf{\text{v}}}_p}{dt}$$

(3226)

液滴-液膜转换条件

液滴液膜转换模型用于确定碰撞壁面的液滴是否会在壁面上形成液膜。

液滴液膜转换模型根据所选择的条件，计算覆盖率或等效液膜厚度。覆盖率条件通常更适用于韦伯数高的内燃模拟。等效液膜厚度条件更加普遍适用。

覆盖率

覆盖率为碰撞液滴覆盖的网格单元壁面的分数。冲击时，假设液滴为圆柱形状且扩散直径为 $D_s$：

$$D_s=0.613D_d{We}_d^{0.39}$$

(3227)

其中：

• $D_d$ 为液滴直径。
• ${We}_d$ 为液滴的韦伯数。

则，液滴覆盖的面积 $A_s$ 如下：

$$A_s=0.25N\pi D_s^2$$

(3228)

其中，$N$ 为液滴数密度。当 $A_s$ 达到为覆盖率属性设置的值时，所有液滴都将融合到液膜中。

此时覆盖率为 ${\gamma }_c=A_s/A_c$，其中，$A_c$ 为网格单元壁面的面积。

等效液膜厚度

等效液膜厚度为 $\delta e$：

$$\delta e=\frac{V_d}{A_c}$$

(3229)

其中，$V_d$ 为网格单元壁面上所有液滴的总体积。当 $\delta e$ 达到为等效液膜厚度属性设定的值时，所有液滴都将融合到液膜中。

贴壁液滴的热和质量传递

通过激活粘附液滴热传递模型，可在过渡沸腾模拟中考虑粘附液滴和壁面之间的热传递。对于壁面温度高于液滴饱和温度的情况，如果激活了粘附液滴质量传递模型，也可能会引发总体泡核沸腾。

热传递

可使用 Eckhause 和 Reitz 提出的方法 [656] 计算粘附在壁面上的液滴的热传递。冲击壁面时，假设粘附液滴（或其任何部分）扩散到圆柱盘，其有效扩散直径 $D_s$ 由以下公式给出：

$$D_s=0.61D_p{We}_p^{0.38}$$

(3230)

其中：

• $D_p$ 为冲击液滴的直径。
• ${We}_p$ 为液滴韦伯数的变体，该项使用液滴密度和壁面与液滴之间相对速度的壁面法向分量：

  $${We}_p=\frac{{\rho }_p{|{\mathbf{v}}_w-{\mathbf{v}}_p|}_n^2{D}_p}{{\sigma }_p}$$

  (3231)

其中，${\sigma }_p$ 是液滴的表面张力。

扩散液滴的厚度根据液滴体积和扩散直径计算得出。在因蒸发/冷凝导致液滴质量发生变化的情况下，假设圆柱盘的高径比保持不变。

一般形式的粘附液滴能量平衡方程如下：

$$m_p{C}_p\frac{d{T}_p}{dt}=Q_c+Q_w+Q_s+{\dot{m}}_p{L}_{\mathrm{e}\mathrm{f}\mathrm{f}}$$

(3232)

其中：

• $m_p$、$C_p$ 和 $T_p$ 分别为液滴的质量、比热和温度。
• $Q_c$ 为连续体相的对流传热率。
• $Q_w$ 为壁面的传热率。
• $Q_s$ 为其他模型或源的能量增加率。
• ${\dot{m}}_p$ 为到颗粒的质量传递率。
• $L_{\mathrm{e}\mathrm{f}\mathrm{f}}$ 为所传递材料的有效潜热。

连续体相的热传递 $Q_c$

连续体相的传热率如下：

$$Q_c=h_g{A}_s(T_g-T_p)$$

(3233)

$$h_g=\mathrm{N}\mathrm{u}\left(\frac{k_g}{D_s}\right)$$

$$\mathrm{N}\mathrm{u}=0.664{\mathrm{Re}}_s^{1/2}{\mathrm{Pr}}^{1/3}$$

$${\mathrm{Re}}_s=\frac{{\rho }_g|{\mathbf{v}}_g-{\mathbf{v}}_p|D_s}{{\mu }_g}$$

其中：

• $h_g$ 为热传递系数。
• $A_s$ 为液滴表面积。
• $k_g$ 为连续体相的导热率。
• ${\mathrm{Re}}_s$、$\mathrm{Pr}$ 和 $\mathrm{N}\mathrm{u}$分别为雷诺数、普朗特数和努赛尔数。努赛尔数根据平板上的层流的 Pohlhausen 相关性计算得出。[651]

壁面热传递

没有粘附液滴质量传递模型时，传导是唯一的热传递模式（请参见下面的“第 1 种情况”）。激活粘附液滴质量传递模型后，根据壁面温度 $T_w$ 与饱和温度 $T_{\mathrm{s}\mathrm{a}\mathrm{t}}$ 和莱登弗洛斯特温度 $T_L$ 的关系区分三种情况：

第 1 种情况：$T_w\le T_{\mathrm{s}\mathrm{a}\mathrm{t}}$

根据下式对导热传递建模：

$$Q_w=h_w{A}_s(T_w-T_p)$$

$$h_w=k_p/\delta$$

其中，$\delta$ 为扩散液滴的厚度，$k_p$ 为液滴导热率。

第 2 种情况：$T_{\mathrm{s}\mathrm{a}\mathrm{t}}{<T}_w\le T_L$

对于 $T_w>T_{\mathrm{s}\mathrm{a}\mathrm{t}}$ 的情况，液滴应用的热传递模式与池内沸腾热传递中相同。根据超温幅值，$\delta T_w=T_w-T_{\mathrm{s}\mathrm{a}\mathrm{t}}$，有四种热传递模式：自然对流、泡核沸腾、过渡沸腾和液膜沸腾。Simcenter STAR-CCM+ 可模拟泡核沸腾和过渡沸腾模式。根据 Rohsenow 池内沸腾相关性，通过壁面传递到液滴的热通量的增幅与 $\delta T_w$ 的三次幂成正比：

$$q_b=\frac{L_{\mathrm{e}\mathrm{f}\mathrm{f}}{\mu }_l}{{\mathrm{Pr}}_l^n}{\left(\frac{g({\rho }_l-{\rho }_v)}{\sigma }\right)}^{\frac{1}{2}}{\left(\frac{C_{p,l}\delta T_w}{C_{sf}{L}_{\mathrm{e}\mathrm{f}\mathrm{f}}}\right)}^3$$

(3234)

其中：

• 带有下标 $l$ 和 $v$ 的属性分别属于液滴和蒸汽相。
• $L_{\mathrm{e}\mathrm{f}\mathrm{f}}$ 为所传递材料的有效潜热。
• $\sigma$ 为液体-汽体交界面的表面张力。
• $C_{sf}$ 为取决于表面-液体组合的系数。
• $g$ 为重力加速度。
• $T_{\mathrm{s}\mathrm{a}\mathrm{t}}$ 为液滴的饱和温度。

普朗特数的 $n$ 指数值也取决于表面-液体组合。对于水-黄铜接触，$C_{sf}$ 和 $n$ 的值分别为 0.006 和 3.0。

注意，$C_{sf}$ 在 Rohsenow 相关性中增加到三次幂，因此极大地影响了热传递。$C_{sf}$ 的可用数据表明不同的流体-表面组合之间存在较大差异。

根据下式，热通量增加到最大值（临界热通量）：

$$q_{\max }=C_{\max }{L}_{\mathrm{e}\mathrm{f}\mathrm{f}}{\rho }_v^{1/2}{\left(\sigma g[{\rho }_l-{\rho }_v]\right)}^{1/4}$$

(3235)

其中，$C_{\max }$ 为用户提供的系数，默认为 0.15。

根据下式，在莱登弗洛斯特温度 $T_L$ 下，热通量从 $q_{\max }$ 线性降低到其最小值 $q_{\min }$ ：

$$q_{\min }=C_{\min }{L}_{\mathrm{e}\mathrm{f}\mathrm{f}}{\rho }_v{\left(\sigma g[{\rho }_l-{\rho }_v]\right)}^{1/4}{({\rho }_l+{\rho }_v)}^{-1/2}$$

(3236)

其中，$C_{\min }$ 为用户提供的系数，默认为 0.09。

使 $q_b$ 和 $q_{\max }$ 相等并求解 $\delta T_w$ ，得出达到最大热通量时的壁面超温 $\delta T_s$。根据这些相关性，模型按如下所示计算壁面的传热率：

$$Q_w=A_s\left\{\begin{array}{cc}\hfill q_b,& \delta T_w<\delta T_s\hfill \\ \hfill q_{\max },& \delta T_w<C_s\delta T_s\hfill \\ \hfill q_{\min }+\frac{\delta T_L-\delta T_w}{\delta T_l-C_s\delta T_S}(q_{\max }-q_{\min }),& \delta T_w<\delta T_L\hfill \end{array}\right\}$$

(3237)

其中，$\delta T_L=T_L-T_{\mathrm{s}\mathrm{a}\mathrm{t}}$，$C_s$ 为模型常数，其默认值设为 1.2。

第 3 种情况：$T_w>T_L$

当壁面温度高于莱登弗洛斯特温度时，假设冲击液滴悬浮在温度与载送流体相同的蒸汽层上。在以下条件下，不考虑直接壁面热传递：$Q_w=0$。

首先应用到液滴的总热传递 $Q_c+Q_w+Q_s$，将液滴温度提高到 $T_{\mathrm{s}\mathrm{a}\mathrm{t}}$（如有必要）；如果激活了可选的粘附液滴质量传递模型，则使用任何余量通过潜热传递蒸发液滴 (${\dot{m}}_p$)。

质量传输

激活粘附液滴质量传递模型时，应考虑两个质量传递源：因泡核沸腾热传递导致的液滴蒸发和下述连续体相的质量传递。

连续体相的质量传递

粘附液滴和周围连续体之间的质量传递率由以下公式给出：

$${\dot{m}}_p=-\left(\frac{{\rho }_v{D}_{g}Sh}{D_s}\right)\left(\frac{\pi }{4}{D}_s^2\right)(Y_{\mathrm{s}\mathrm{a}\mathrm{t}}-Y_{\infty })$$

(3238)

$$\mathrm{S}\mathrm{h}=0.664{\mathrm{Re}}_s^{1/2}{\mathrm{S}\mathrm{c}}^{1/3}$$

其中：

• ${\rho }_v$ 为在连续体相温度下计算的液滴蒸汽密度。
• $Y_{\mathrm{s}\mathrm{a}\mathrm{t}}$ 为颗粒表面处颗粒蒸汽的质量分数。
• $Y_{\infty }$ 为周围载送流体中颗粒蒸汽的质量分数。
• $D_g$ 为连续体相的质量扩散率
• $\text{Sc}$ 和 $\text{Sh}$ 分别为施密特数和舍伍德数。

舍伍德数根据 Pohlhausen 相关性 [651] 计算。