侵蚀

侵蚀模型模拟两种侵蚀机制：冲击磨损和磨损。

冲击磨损可预测颗粒对侵蚀表面的直接冲击产生的侵蚀率。磨损可预测颗粒对表面的磨损产生的侵蚀率。

侵蚀模型使用壁面旁边网格单元中的颗粒相信息来确定以下物理量：

颗粒体积分数和颗粒温度用于确定单位时间内冲击单位壁面面积的颗粒质量流率 ${\dot{m}}_{p}$ 。与壁面相邻的颗粒速度用于将 ${\dot{m}}_{p}$ 与壁面材料的质量损耗率关联。

冲击磨损侵蚀

冲击侵蚀率定义为单位时间内单位面积中被侵蚀的壁面材料的质量：

图 1. EQUATION_DISPLAY

E_{f} = {\dot{m}}_{p} e_{r}

(2394)

其中：

下图是单个颗粒接近壁面的示意图：

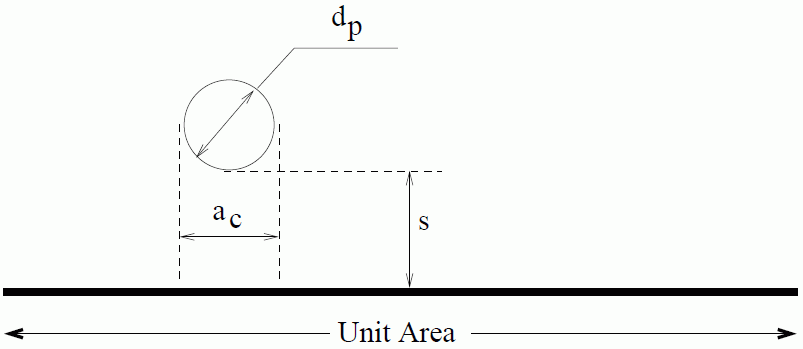
其中：

撞击单位面积的颗粒的质量流率由以下公式给出：

图 2. EQUATION_DISPLAY

{\dot{m}}_{p} = M_{p} C_{p} N_{p}

(2395)

其中：


图 3. EQUATION_DISPLAY $M_{p} = ρ_{p} \frac{π}{6} d_{p}^{3}$ (2396)	单个颗粒的质量
图 4. EQUATION_DISPLAY $C_{p} = \frac{\sqrt{3 θ_{p}}}{s}$ (2397)	每个颗粒的碰撞频率
图 5. EQUATION_DISPLAY $N_{p} = \frac{1}{a_{c}}$ (2398)	与单位面积相邻的颗粒数
图 6. EQUATION_DISPLAY $s = d_{p} [{(\frac{α_{\max}}{α_{p}})}^{\frac{1}{3}} - 1]$ (2399)	边界和相邻颗粒表面之间的平均距离
图 7. EQUATION_DISPLAY $a_{c} = d_{p}^{2} {(\frac{α_{\max}}{α_{p}})}^{\frac{2}{3}}$ (2400)	每颗粒的平均边界面积
$α_{p}$	颗粒体积分数
$α_{\max}$	最大填充体积分数

替换这些物理量并简化 Eqn. (2394)，可得到侵蚀率的最终形式：

图 8. EQUATION_DISPLAY

E_{f} = \frac{π}{6} ρ_{p} \sqrt{3 θ_{p}} \frac{α_{p} g_{0}}{α_{\max}} e_{r}

(2401)

其中：

如果使用多种颗粒相，则当计算每种颗粒相的贡献时， $α_{p}$ 将替换为累积颗粒体积分数 $α_{c u m u l}$ 。

欧拉多相模拟中的侵蚀率 $e_{r}$ 使用的侵蚀相关性与拉格朗日和 DEM 多相模拟中使用的相同：

磨损率 $E_{w}$ 定义为单位时间内在单位面积由于磨损而被侵蚀的壁面材料质量。

磨损侵蚀的壁面材料质量由下面的 Archard 公式给出。

图 9. EQUATION_DISPLAY

m_{w} = a F s

(2402)

其中：

因此， $E_{w}$ 为：

图 10. EQUATION_DISPLAY

E_{w} = a P U_{s}

(2403)

其中：

法向压力 $P$ 为：

图 11. EQUATION_DISPLAY

P = {\dot{m}}_{p} U_{n}

(2404)

其中：

Eqn. (2395) 中描述了 ${\dot{m}}_{p}$ 的公式。

因此，欧拉多相中磨损率的最终形式为：

图 12. EQUATION_DISPLAY

E_{w} = a \frac{π}{6} ρ_{p} \sqrt{3 θ_{p}} \frac{α_{c u m u l} g_{0}}{α_{\max}} U_{n} U_{s}

(2405)