结晶

Simcenter STAR-CCM+ 中实现了溶质结晶模型和熔体结晶模型。

成核

空间齐次群体平衡方程 (PBE) 的最简单形式为：

图 1. EQUATION_DISPLAY

\partial_{t} n = - \partial_{L} (2 G n) + {\dot{N}}_{0} δ (L - L_{0})

(2406)

其中：

$n (L)$ 为颗粒尺寸分布 (PSD)，直径为 $L$ 的颗粒的数密度。
$G = \frac{1}{2} \partial_{t} L$ 为考虑颗粒表面相变的增长率。
${\dot{N}}_{0}$ 为成核速率。
$L_{0}$ 为核直径。

溶液中的溶质浓度 $C_{l}$ 由平流-扩散-反应方程控制：

图 2. EQUATION_DISPLAY

\partial_{t} ρ_{l} α_{l} C_{l} + \nabla\cdot ρ_{l} α_{l} (C_{l} u_{l} - D_{T} \nabla C_{l}) = - S_{c}

(2407)

其中，汇项 $S_{c}$ 通过在整个颗粒-液体交界面上对面网格增长率进行积分并创建新颗粒给出：

图 3. EQUATION_DISPLAY

S_{c} = π \int ρ_{s} n (L) L^{2} G d (L) + ρ_{s} {\dot{N}}_{0} \frac{π}{6} L_{0}^{3}

(2408)

以下示意图显示了颗粒的质量和能量平衡：

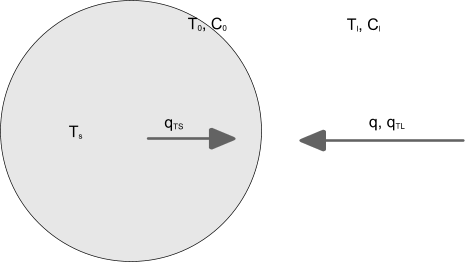
颗粒内部的温度为 $T_{s}$ 。在交界面中，溶质浓度为 $C_{0}$ ，其对应温度为 $T_{0}$ 。在液体中，温度为 $T_{l}$ ，溶质浓度为 $C_{l}$ 。表面溶质的质量通量 $q$ 由晶体增长率 $ρ_{s} G$ 平衡。热将从液体和颗粒内部传递到表面：相应的通量为 $q_{T L}$ 和 $q_{T S}$ 。

质量和能量平衡为：

图 4. EQUATION_DISPLAY

q = ρ_{s} G

(2409)

图 5. EQUATION_DISPLAY

q_{T L} + q_{T S} = - q H_{c}

(2410)

其中， $H_{c}$ 为结晶焓。

一般而言，Eqn. (2409) 和 Eqn. (2410) 适用于几乎所有质量传递过程（例如，沸腾、不均匀燃烧）。但考虑到数值，同时为了用户方便，需要进一步区分这些模型。

可以区分浓度驱动（溶质）结晶和温度驱动（熔体）结晶（Mullin，[522]）。

溶质结晶

在溶质结晶过程中，化合物（溶质）将在另一种液体（溶剂）中溶解。当温度下降或添加抗溶剂时，溶质的浓度将高于饱和浓度，随即开始结晶。

面网格增长率 $G$ 是过饱和函数（Mullin，[522]；Borissova，[434]）：

图 6. EQUATION_DISPLAY

G = k_{g} {(Δ C)}^{m_{g}}

(2411)

其中， $k_{g}$ （前因子）和 $m_{g}$ （指数）为经验参数。

饱和浓度 $C_{s a t} (T)$ 为温度函数。过饱和增量 $Δ C = C_{0} - C_{s a t}$ 为颗粒周围液膜中的溶质浓度与饱和浓度之差。

通常，溶解过程快于结晶过程（Mullin，[522]），因此对 Eqn. (2411) 的参数进行了划分：

图 7. EQUATION_DISPLAY

k_{g} = {\begin{matrix} k_{g}^{+}, & C_{s a t} \geq 0 \\ k_{g}^{-}, & C_{s a t} < 0 \end{matrix}

(2412)

图 8. EQUATION_DISPLAY

m_{g} = {\begin{matrix} m_{g}^{+}, & C_{s a t} \geq 0 \\ m_{g}^{-}, & C_{s a t} < 0 \end{matrix}

(2413)

相变由相应的液膜质量传递平衡；质量平衡为：

图 9. EQUATION_DISPLAY

q = ρ_{s} G = ρ_{l} S h \frac{D}{L} (C_{l} - C_{0})

(2414)

其中：

$q$ 为质量通量
$S h$ 为舍伍德数
$D$ 为分子扩散系数
$ρ_{s}$ 和 $ρ_{l}$ 分别为固相和液相的密度。

液膜能量平衡包括内部和外部热传递，如下所示：

图 10. EQUATION_DISPLAY

N u \frac{λ_{l}}{L} (T_{l} - T_{0}) = F o \frac{λ_{s}}{L} (T_{0} - T_{s}) - q H_{c}

(2415)

其中：

$N u$ 为努赛尔数
$F o$ 为傅立叶数
$λ_{l}$ 和 $T_{l}$ 为液相的导热率和温度
$λ_{s}$ 和 $T_{s}$ 为固相的导热率和温度。

Simcenter STAR-CCM+ 实施遵循其他模型（例如，蒸发）的实现并假设 $F o = \infty$ ，即 $T_{0} = T_{s}$ 。

熔体结晶

与其溶质结晶不同，熔体结晶可以发生在单组分液体中（例如，在水中结冰）。在液体中溶解的外加剂也十分重要。首先，外加剂降低了饱和温度。例如，海水冻结温度低于淡水冻结温度。其次，晶体的成分与熔体的成分不同。例如，熔体结晶过程在食品工业和海水淡化领域中十分重要（Rahman，[530]；Casenave，[438]）。

增长率由以下公式给出（Mullin，[522]）：

图 11. EQUATION_DISPLAY

G = {\begin{matrix} k_{g}^{+} {(Δ T)}^{m_{g}^{+}} C_{0}, & Δ T \geq 0 \\ k_{g}^{-} {(Δ T)}^{m_{g}^{-}}, & Δ T < 0 \end{matrix}

(2416)

其中， $Δ T = T_{0} - T_{s a t}$ 为温度过饱和。与溶质结晶一样，融化（溶解）通常快于晶体增长，因此将 Eqn. (2416) 的参数分成两个集合。

增长取决于晶体表面上的冻结组分浓度，由于假设晶体为单组分，因此融化与浓度无关。在当前实现的熔体结晶模型中得到了进一步简化：假设 $C_{0} = C_{l}$ 。对于高质量传递率和（或）慢增长率，这种假设（Casenave，[438]）合理。

熔体结晶的质量和能量平衡为：

图 12. EQUATION_DISPLAY

q = ρ_{s} G

(2417)

图 13. EQUATION_DISPLAY

q_{T S} = N u \frac{λ_{l}}{L} (T_{s} - T_{l}) - q H_{c}

(2418)

Armenante-Kirwan 相关性

努赛尔数和舍伍德数的标准 Ranz-Marshall 相关性假设热传递和质量传递通过平均相间滑移速度来放大。对于小颗粒，平均滑移较小，但实验表明传递可通过湍流增强。Armenante 和 Kirwan ([428]) 提出了微颗粒质量传递模型。

文献（Pangarkar，[527]）中记载了许多类似的模型。但是，考虑到实验数据的不确定性，Simcenter STAR-CCM+ 通过用户控制的参数实现了新模型：

图 14. EQUATION_DISPLAY

N u = 2.0 + α {Re}_{T}^{β} \Pr^{γ} {(\frac{Δ ρ}{ρ_{l}})}^{δ}

(2419)

图 15. EQUATION_DISPLAY

S h = 2.0 + α {Re}_{T}^{β} {S c}^{γ} {(\frac{Δ ρ}{ρ_{l}})}^{δ}

(2420)

其中，湍流雷诺数 ${Re}_{T}$ 为：

图 16. EQUATION_DISPLAY

{Re}_{T} = \frac{ϵ^{1 / 3} L^{4 / 3}}{ν}

(2421)

其中， $ϵ$ 为单位质量流体的功率输入。

系数默认值为 $α = 0.52$ ， $β = 0.52$ ， $γ = 0.333$ ， $δ = 0.0$ 。

这些值可由用户指定。请参见舍伍德数属性和努赛尔数属性。