接触角

接触角 $\theta$ 描述固体壁面对表面张力的影响。

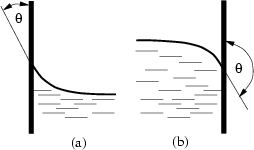
在三相交线（即壁面和流体接触的线）处测量接触角。在 Simcenter STAR-CCM+ 中，对于相间相互作用，可将一个流体设为主相，其他流体设为次相。接触角的值小于 $90°$ 意味着主相正在湿润壁面，如下图中的 (a) 部分所示：

当接触角还取决于三相交线速度时，它称为动态接触角。一些简单模型基于使用单一前进和撤回角的阶跃函数，而其他模型使用平滑阶跃函数。这些模型适合于惯性主导的流体，因为动态接触角不高度依赖于速度。

Simcenter STAR-CCM+ 实现 Kistler 相关性，这对毛细管主导的流体非常适用。

无量纲毛细管数 $Ca$ 定义为：

其中：

• $V$ 为三相交线特征速度
• $\mu$ 为主相（通常为液相）的动力粘度
• $\sigma$ 为表面张力

三相交线速度定义为：

其中：

• $\mathbf{V}$ 为三相交线处流体和对应壁面的相对速度。
• ${\hat{n}}_t$ 是所指方向与主相的体积分数梯度 ( $\nabla \alpha$ ) 的方向相同的正切方向上的单位矢量

动态接触角模型尝试考虑前进和撤回接触角对三相交线速度的依赖性。

Kistler 相关性

Simcenter STAR-CCM+ 可实现 Kistler 相关性 [624]，其为基于毛细管数 $Ca$ 且利用 Hoffman 函数的经验动态接触角相关性。Kistler 接触角定义为：

$${\theta }_k=f_{Hoff}(Ca+f_{Hoff}^{-1}\left({\theta }_s\right))$$

(2616)

其中， $f_{Hoff}$ 为 Hoffman 函数：

$$f_{Hoff}\left(x\right)={\cos }^{-1}(1-2\tanh \left(5.16{\left(\frac{x}{1+1.31x^{0.99}}\right)}^{0.706}\right))$$

(2617)

其中， $f_{Hoff}^{-1}$ 为其逆函数。Simcenter STAR-CCM+ 使用稍加修改的 Hoffman 函数定义实现其逆函数的封闭形式。在修改的 Hoffman 函数中，分母中的 $x^{0.99}$ 项更改为简单的 $x$ 。逆函数的封闭形式适用于 0–176 度范围内的接触角值。大于上限的前进或撤回接触角限制为 176 度。

静态接触角 ${\theta }_s$ 将作为静态前进或撤回接触角插入 Eqn. (2616)，具体取决于毛细管数的符号。在前进/撤回属性中， ${\theta }_s$ 指定为前进接触角或撤回接触角。

混合 Kistler 相关性

使用此方法可增强 Kistler 方法的稳定性。在 Simcenter STAR-CCM+ 中，可以为平衡毛细管数 ( ${Ca}_{eq}$ ) 定义范围。在指定的范围 $-{Ca}_{eq}<Ca<{Ca}_{eq}$ 内，产生的动态接触角与平衡接触角 ( ${\theta }_e$ ) 混合作为加权平均值：

$${\theta }_d=f{\theta }_e+(1-f){\theta }_k$$

(2618)

虽然 ${\theta }_e$ 是用户指定的值，但是因子 $f$ 在 ${Ca}_{eq}$ 范围内确定为：

$$f=0.5+0.5\cos \left(\frac{Ca}{{Ca}_{eq}}\pi \right)$$

(2619)