蒸发和冷凝

蒸发是当具有足够高动能的液体分子或原子通过两个相之间的交界面脱离时发生的一种汽化形式（从液体到气体的相变）。冷凝是反向汽化过程，是从气体到液体的相变。

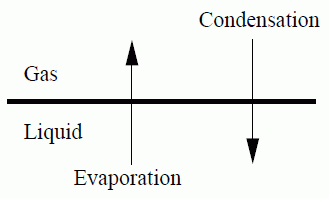
在 Simcenter STAR-CCM+ 中，蒸发和冷凝用于处理在液相和气相之间的自由表面交界面处发生的蒸发（无沸腾）和冷凝。这两个相都建模为多组分混合物，可以包含非相互作用（惰性）组分 [606]、[605]。蒸发和冷凝可视为流体动力受限，即认为相在交界面处于平衡状态，驱动力为组分的扩散。 Raoult 定律用于描述相平衡。

特定组分 $i$ 的蒸发率 (kg/s m²) 由以下公式给出：

图 1. EQUATION_DISPLAY

{\dot{m}}_{i} = - \frac{ρ_{g} D_{g, i} \frac{\partial Y_{g, i}}{\partial n} |_{s}}{1 - \sum_{j = 1}^{N_{v}} Y_{g, j}^{s}}

(2660)

其中：

$ρ_{g}$ 为气相的密度
$Y^{s}$ 为表面的组分质量分数
$D_{g, i}$ 为扩散系数
$N_{v}$ 为正在发生蒸发或冷凝的组分总数
下标 $g$ 表示气相变量

组分的蒸气压 $p_{i}$ 为：

图 2. EQUATION_DISPLAY

p_{i} = a_{i} {p_{i}}^{*}

(2661)

其中， ${p_{i}}^{*}$ 为纯组分 $i$ 的蒸气压， $a_{i}$ 为取决于液体混合物的活性。此表达式可以写为：

图 3. EQUATION_DISPLAY

p_{i} = γ_{i} X_{L, i} {p_{i}}^{*}

(2662)

其中， $γ_{i}$ 为考虑与混合物理想行为的偏差的活性系数。

Raoult 定律规定 $γ_{i} \approx 1$ ，此处采用近似。给定组分蒸气压，其在交界面处的摩尔分数可以根据以下方程推导得出：

图 4. EQUATION_DISPLAY

X_{g, i}^{s} = \frac{p_{i}}{p}

(2663)

其中， $p$ 为压力。通过以下方程即可转换为交界面蒸汽质量分数：

图 5. EQUATION_DISPLAY

Y_{g, i}^{s} = \frac{X_{i}^{s} W_{i}}{\sum_{j = 1}^{N_{v}} X_{j}^{s} W_{j} + \sum_{j = 1}^{N_{g, p}} X_{j}^{s} W_{j}}

(2664)

其中， $N_{g, p}$ 为气相中的惰性组分数。尽管已知蒸发组分的摩尔分数，但惰性组分（未发生蒸发或冷凝）的摩尔分数未知。合理的近似法就是引入背景摩尔量，该项在与交界面相隔一小段距离的位置处计算：

图 6. EQUATION_DISPLAY

W_{b g} = \frac{\sum_{j = 1}^{N_{g, p}} X_{j} W_{j}}{\sum_{j = 1}^{N_{g, p}} X_{j}}

(2665)

交界面背景摩尔分数为：

图 7. EQUATION_DISPLAY

X_{b g}^{s} = 1 - \sum_{j = 1}^{N_{v}} X_{j}^{s}

(2666)

因此，交界面蒸汽质量分数可以近似为：

图 8. EQUATION_DISPLAY

Y_{g, i}^{s} \approx \frac{X_{i}^{s} W_{i}}{\sum_{j = 1}^{N_{v}} X_{j}^{s} W_{j} + X_{b g}^{s} W_{b g}}

(2667)

对于每个相互作用组分，Eqn. (2660) 的数值解从定义以下标量函数 $Y_{g, m}$ 开始：

图 9. EQUATION_DISPLAY

Y_{g, m} = α_{l} Y_{g, i}^{s} + α_{g} Y_{g, i}

(2668)

其中， $α_{l}$ 为液相体积分数， $α_{g}$ 为气相体积分数。可按如下所示计算得出一个网格单元的近似蒸发率 ${\dot{M}}^{'}_{i, c}$ ：

图 10. EQUATION_DISPLAY

{\dot{M}}^{'}_{i, c} \approx - \frac{ρ_{g} D_{g, i} \nabla Y_{g, m} \nabla α_{l} V_{c}}{1 - \sum_{j = 1}^{N_{v}} Y_{g, j}^{s}}

(2669)

根据液相分数梯度 $\nabla α_{l}$ 在一定体积内的积分表示其包含的交界面面积 [580]、[591]。

通过比较 Eqn. (2660) 和 Eqn. (2669) 可以看出， $\nabla Y_{g, m}$ 表示 $\nabla Y_{g, i}$ 的效应。最低阶分析显示在准稳态状态下，蒸发率的相对误差表现为：

图 11. EQUATION_DISPLAY

ε_{r e l} \approx \frac{1}{H | \nabla α |}

(2670)

其中， $H$ 表示交界面上的边界层的厚度。

因此，精度取决于与边界层相比确定交界面的位置的准确程度。如果交界面未弥散开，则体积分数的梯度幅值倒数 ${| \nabla α |}^{- 1}$ 是网格尺寸的度量。此条件强调需要一个足够细的网格，以便准确地对组分远离和朝向交界面的输运进行建模。类似的注意事项对交界面附近的温度和压力梯度同样有效。

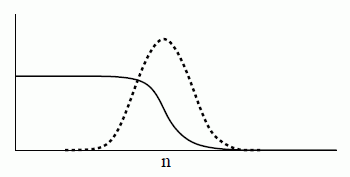
根据 Eqn. (2669)，组分、相和连续体的源分布在构成交界面（使用非消隐的体积分数梯度）的网格单元上，如上图所示。该图描绘了自由表面交界面上的 $α_{l}$ （实线）和 $- | \nabla α_{l} |$ （虚线）的典型行为，以及表面法向坐标 $n$ 。