凝固导致的流体阻力

融化与凝固模型仅模拟相变对能量方程的影响；它不会修改动量方程。需要其他模型才能考虑从液态到固态的材料属性更改。

浆料粘度模型

在凝固的早期阶段，小晶体在熔体中成核并生长。这些晶体随液体一起移动，但彼此之间不相互作用。固体相和液体相的混合物称为浆料。但是，液体中存在固体晶体会增大两相混合物的粘度，从而增加流体阻力。此增加的阻力使用浆料粘度模型进行模拟。

浆料粘度模型适用于固相体积分数的低值， ${\alpha }_s^{*}\le {\alpha }_{\mathrm{cr}}^{*}$ ，其中，临界固体分数 ${\alpha }_{cr}$ 定义适用性的上限。

Metzner 的方法 ([594]) 将混合物的粘度变化表示为固相体积分数 ${\alpha }_s^{*}$ 的函数：

$$\mu \text{*}={\mu }_l\left[{(1-\frac{F_{\mu }{\alpha }_s^{*}}{A})}^{-2}-1\right]$$

(2713)

其中：

• ${\mu }^{*}$ 为固体-液体混合物的有效粘度
• ${\mu }_l$ 为液体的动力粘度
• $F_{\mu }$ 为 Eqn. (2719) 给定的切换函数
• $A$ 为取决于晶体的长宽比和表面粗糙度的晶体常数。

两相区渗透率模型

对于高固相体积分数，等轴颗粒生长，开始凝聚并形成枝晶区域。枝晶还从冷却固体表面或凝固前沿生长到熔体中。枝晶渗透的部分凝固固定区域称为“两相区”。

此模型的常见工程应用是高压压铸，其中熔体以高速和低于固相线温度的壁面温度通过管道压缩。熔体在壁面处凝固，枝晶从凝固前沿生长到熔体。此部分凝固的区域导致管道中出现影响熔体质量流量的额外压力损失。此压力损失使用两相区渗透率模型进行模拟。

Carman-Kozeny 两相区渗透率方法为流体阻力提供两相区，无需设置多孔介质。此外，此方法在融化与凝固过程中更新速度场。流体阻力仅在固相体积分数大于零的网格单元中处于活动状态，且应用于物理连续体中的所有区域。

与各向同性多孔介质类似，可以对两相区中的流体阻力建模。因此，要量化渗透率，需要使用通过多孔介质的流量的 Carman-Kozeny 方程[583]：

$$K=\frac{{\left(1-{\alpha }_s^{\text{*}}\right)}^3}{{\alpha }_s^{\text{*2}}{F}_K{c}_s}$$

(2714)

其中：

• $K\left[m^2\right]$ 为渗透率
• ${\alpha \text{*}}_s$ 为相对固相体积分数
• $F_K$ 为 Eqn. (2720) 给定的无量纲切换函数。
• $c_s$ 为形状因子：

$$c_s=c/d^2$$

(2715)

其中，$c$ 为形状常数，默认值为 180；$d$ 为二次枝晶间距。

两相区渗透率对动量方程 Eqn. (2588) 的影响将进入多孔介质阻力 ${\mathbf{\text{f}}}_p$：

$${\mathbf{\text{f}}}_p=-{\mathbf{\text{P}}}_{\text{v, Mushy Zone}}\cdot \mathbf{\text{v}}$$

(2716)

其中，$\mathbf{\text{P}}$ 为多孔阻力张量，由以下公式给出：

$${\mathbf{\text{P}}}_{\mathrm{MushyZone}}=(\frac{{\mu }_l}{K}+\frac{C_F{\rho }_l{\alpha }_l^{*}}{\sqrt{K}}\Vert \mathbf{\text{v}}\Vert )$$

(2717)

${\mathbf{\text{P}}}_{\text{v}}$ 和 ${\mathbf{\text{P}}}_{\text{i}}$ 分别为粘性（线性）和惯性（二次）阻力张量。

两相区渗透率对 ${\mathbf{\text{P}}}_{\text{v}}$ 的影响通过以下公式体现：

$${\mathbf{\text{P}}}_{\text{v, Mushy Zone}}=(\frac{{\mu }_l}{K}+\frac{C_F{\rho }_l{{\alpha }^{*}}_l}{\sqrt{K}}\Vert \mathbf{\text{v}}\Vert )$$

(2718)

其中：

• $\frac{{\mu }_l}{K}$ 为达西项
• $\frac{C_F{\rho }_l{{\alpha }^{*}}_l}{\sqrt{K}}\Vert \mathbf{\text{v}}\Vert$ 为 Forchheimer 项

其中：

• $C_F$ 为 Ergun 系数
• ${\rho }_l$ 为液相密度
• ${\alpha }_l^{*}$ 为 ${\alpha }_l^{*}=\left(1-{\alpha }_s^{*}\right)$ 给定的液体分数。

${\mathbf{\text{P}}}_{\text{v,MushyZone}}$ 可以视为曳力系数。曳力系数由达西项和 Forchheimer 项给定，通常称为“粘性曳力”和“形曳力”项。

Forchheimer 项可选，可以停用其对两相区渗透率的影响。当预计枝晶间流体流速较高时，必须考虑 Forchheimer 项。这种高速度对于在压铸或挤压铸造中强化相有重要作用。

Metzner 浆料粘度和 Carman-Kozeny 两相区渗透率模型的切换函数

Metzner 浆料粘度模型和 Carman-Kozeny 两相区渗透率模型通常组合使用。这两种模型覆盖凝固状态的不同范围。每个模型的适用性取决于液体凝固的程度。

使用相对固相体积分数 ${\alpha \text{*}}_s$ 表示凝固状态。临界相对固体分数 ${\alpha }_{\mathrm{cr}}^{*}$ 分隔两个模型的适用性范围。

${\alpha }_s^{*}\le {\alpha }_{\mathrm{cr}}^{*}$	Metzner 浆料粘度模型
${\alpha }_{\mathrm{cr}}^{*}<{\alpha }_s^{*}$	Carman-Kozeny 两相区渗透率模型

对于 Metzner 浆料粘度模型和 Carman-Kozeny 两相区模型，切换函数可确保每个模型在其固相体积分数相应范围内应用。切换函数作为倍增因子应用于各个模型方程（请参见 Eqn. (2713) 和 Eqn. (2714)）。

浆料粘度模型的切换函数为：

$$F_{\mu }\left({\alpha \text{*}}_s\right)=0.5-\frac{\text{arctan}\left[s\left({\alpha \text{*}}_s-{\alpha \text{*}}_{\mathrm{cr}}\right)\right]}{\pi }$$

(2719)

其中，$s$ 为切换函数常数。

两相区渗透率模型的切换函数由以下公式给出：

$$F_K\left({\alpha \text{*}}_s\right)=1-F_{\mu }\left({\alpha \text{*}}_s\right)=0.5+\frac{\text{arctan}\left[s\left({\alpha \text{*}}_s-{\alpha \text{*}}_{\mathrm{cr}}\right)\right]}{\pi }$$

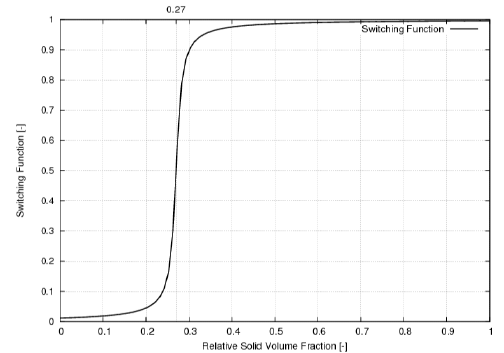
(2720)

切换函数具有临界相对固相体积分数 ${\alpha \text{*}}_{cr}$ 附近的平滑过渡（请参见下图），其中固体颗粒已开始凝聚到很大程度：

无量纲常数 $s$ 的默认值为 100，因为对于 80 和 120 之间的值，形状不太敏感。根据铝合金 A201 的 Baeckerud 公式和其他 [579]，临界固相体积分数 ${\alpha \text{*}}_{cr}$ 的默认值为 0.27。

Oldenburger 和 Spera [600] 最初建议了此切换函数。Simcenter STAR-CCM+ 中实现的切换函数是根据 Chang 和 Stefanescu 的模型 [585] 稍作修改的公式。

下图描述了临界固相体积分数 ${\alpha }_{cr}^{\text{*}}=0.27$（默认值）的切换函数 $F_K$。